基于分布式协商的多无人机目标覆盖与连通保持算法

陶忠良 蒲志强 王乐乐 付清旭 耿虎军

1.中国科学院大学人工智能学院 北京 100049 2.中国科学院自动化研究所 北京 100190 3.中国电子科技集团公司第五十四研究所 河北石家庄 050080

多无人机具有分布性、灵活性、简单性等优势,可以完成单架无人机无法完成的复杂任务,在军事作战[1]、搜索救援[2]、编队表演[3]等领域具有广泛的应用前景.特别是在现代化的军事作战场景中[4-5],指挥中心与作战单元、作战单元与作战单元之间的通信交流是影响胜负的重要因素,一个经典应用场景是利用多无人机快速形成区域通信覆盖,对覆盖范围内我方特定目标群体提供通信支援以增强通信质量,对敌方特定目标群体进行通信干扰以阻碍敌方通信交互.其中,多无人机与目标的合理匹配是提高目标覆盖率的重要影响因素,因此,目标的覆盖问题可归结为目标的优化分配问题.然而,当无人机的覆盖能力有限、目标类型多样、目标价值各异时,多目标优化分配是一个较为困难的求解问题.同时,由于无人机自身的通信距离有限,为了满足无人机之间的信息传递需求,无人机需要时刻保持通信连通.但在无人机规模较大时,同时实现协同覆盖并保持通信实时连通更是一个复杂的多任务组合优化问题.此外,为满足实际应用需求,需考虑无人机仅已知自身与邻居的局部信息条件下的分布式求解框架.综上所述,在局部信息条件和受限的通信距离、覆盖能力等约束条件下,大规模无人机同时实现多类目标的协同覆盖和通信连通保持,是一个极具挑战的理论和应用问题.

针对协同覆盖问题,相关研究者提出了一系列启发式的优化算法.其中,文献[6-7]采用贪婪策略来寻找多目标优化分配覆盖问题的次优解.Zhang 等提出了分布式自适应反演控制方法来实现动态多目标跟踪覆盖[8].Lyu 等提出了一种螺旋算法,实现分配尽可能少的无人机去覆盖所有地面目标[9].以上研究在目标覆盖问题上提供了较优的解决方案,但与许多研究[10-12]类似,均假设无人机的通信范围足够大,从而在默认通信连通的情况下重点研究目标的分配覆盖问题.

为了保证连通性,Reily 等人通过设计多个领导者之间相互保持通信来实现整个全局的连通[13],但在这种控制方式下,跟随者被束缚在领导者通信范围内,降低了群体的灵活性.受生态学启发,Egerstedt 等设计了控制屏障函数（control barrier functions,CBF）对连通性与覆盖率进行优化[14],随后文献[15]基于CBF采用集中式优化的方式来保证通信连通.文献[16]提出了一种连通约束下的感知覆盖策略并获得了较好的覆盖效果,为通信连通保持约束下的目标覆盖问题提供了有效的解决方案.但由于以上集中式控制方法存在中央处理器单点故障问题以及可扩展性差等缺点,在多无人机的多目标覆盖中,分布式控制方法提供了另一种更实用的解决方案,因此,一些研究者提出了分布式控制方案.基于梯度下降法,文献[17-19]实现了一种具有区域覆盖目标的鲁棒分布式连通保持方法,在应用于多目标覆盖场景时,虽然可以通过适当的参数调整来保证连通性,但由于采取梯度下降法对智能体的移动产生较大约束,降低了目标的覆盖性能,因此,很难在保持连通性的同时尽可能覆盖更多的目标.

针对上述文献的不足,同时考虑无人机通信连通性要求、对目标覆盖能力有限、不同目标类型以及目标价值各异等因素,本文提出了一种基于分布式协商的多无人机目标覆盖与连通保持算法.由于Choi 等提出的基于分布式共识的拍卖算法（consensus-based auction algorithm,CBAA）可以有效解决多目标无冲突分配问题[20],因此,本文以CBAA 为基础构建分布式协商机制.设计了基于无人机覆盖能力的目标分组方法来对目标进行分组,将单架无人机所能覆盖的目标数量上限打包为单个目标,从而将单无人机-多目标的覆盖问题转化为单无人机-单目标的覆盖问题；设计目标拍卖规则来对目标进行拍卖,以获得比当前覆盖目标收益更大的目标列表；通过设计协商一致及连通保持机制,来指导多无人机在目标优化分配的同时考虑通信连通保持行为；分别设计了在不同目标数量、不同目标类型,以及不同目标价值等参数下的仿真实验,从而验证算法的有效性.

本文主要贡献归纳：1）提出了基于无人机覆盖能力的目标分组方法.将目标进行按类分组并限制每组的目标数量在无人机的覆盖能力内,将得到的每个组视为无人机覆盖的新目标,从而同时解决了无人机覆盖能力有限以及目标不同类型的问题.2）基于CBAA 设计了协商一致与连通保持机制.通过分布式协商的方式实现无冲突的目标优化分配,同时保持通信连通性.3）设计了连通支援机制来提高无人机的协同性能.当无人机前往覆盖某个目标会对通信连通带来破坏时,通过向邻居发出连通支援请求,从而在保证连通性的同时实现分布式架构下的良好协同性.

1 问题描述及基础知识

1.1 问题描述

假如初始时刻已通过某种方式实现全局连通（如基于全局信息的覆盖方法）,无人机的任务是在接下来的时间内,仅在获取局部信息的条件下,通过分布式协商方式来对目标进行协商分配,同时考虑通信连通性来实现目标优化覆盖和连通保持.假定目标进入无人机的覆盖范围即可对目标进行通信支援或通信干扰,因此,本文将无人机对地面多目标的通信支援与干扰归结为一类通信连通保持与动态多目标的优化覆盖问题,并建模为：

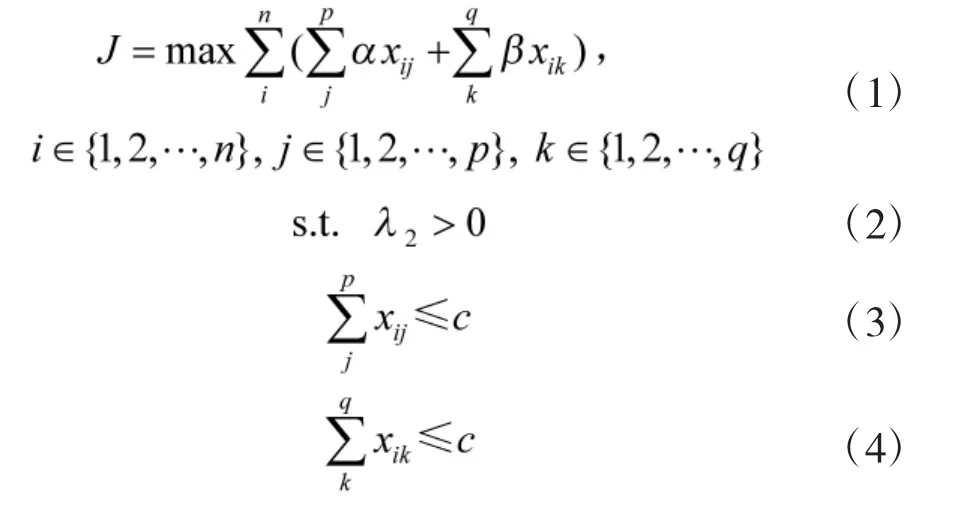
其中,式（1）中xij和xik为决策变量,如xij=1 表示无人机i 前往覆盖我方目标j,反之xij=0；式（2）中是无人机的通信约束项,具体将在2.2 节中作出说明；式（3）与式（4）为无人机最大目标覆盖能力约束项,即无人机i 最多只能覆盖c 个目标；式（5）中xi为无人机覆盖目标类型约束条件,即无人机i 只能同时覆盖一类目标,其中,xi=xij+xik.

上述问题场景及建模方式除适用于多无人机通信覆盖外,同样适用于多无人机协同态势感知、协同灾害救援、协同目标跟踪等场景.因此,本文所针对的是一类典型的实际应用场景.

1.2 基础知识

1.2.1 网络的连通性判定

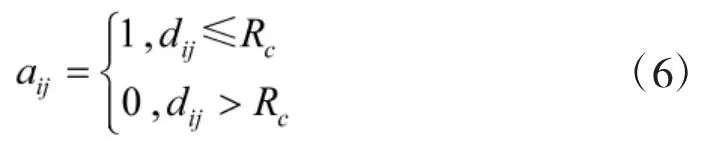
其中,Rc为无人机的通信半径,dij为无人机i 与无人机j 之间的距离大小,当时表示可进行通信并设置aij=1,反之aij=0.文中无人机只能与通信范围内的其他无人机进行通信,这些无人机可以用一个邻居集表示.

图的连通性与拉普拉斯矩阵密切相关,任意一个拓扑图G 的结构特性都可以用拉普拉斯矩阵L=D-A等价表示,其中,D 为度矩阵,也是一个对角矩阵,其对角线上的元素为节点的邻居数；A 为上文中所提到的邻接矩阵,用于表示节点之间的连接关系.由文献[21-22]知,图G 的连通性可由拉普拉斯矩阵的第二小特征值进行判定：当＞0 时,可判定图G 是连通的,且该值越大,图的连通度越强；当=0 时,可得知图G 不连通.如图1判断图G 的连通性为例,首先由图的度矩阵D 和邻接矩阵A 计算得到图的拉普拉斯矩阵L；其次再计算拉普拉斯矩阵的第二小特征值；最后由＞0 可进一步判断得到图G 为一个连通图.

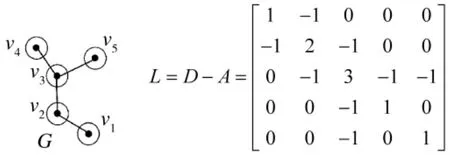
图1 判断图的连通性Fig.1 Connectivity of graphs judges by

1.2.2 地图栅格化

考虑到正六边形可以实现无重叠和无缝隙排布,文中采用六边形栅格化的方式来实现地图离散化表达,并设置正六边形的边长等于无人机的覆盖半径Rr.如图2所示,无人机的覆盖范围正好为正六边形的外接圆范围,因此,当无人机处于正六边形栅格中心时,正好可以实现对该正六边形栅格区域中目标的完全覆盖,同时无人机的运动转化为不同栅格中心点的跳动,由此简化了问题求解.

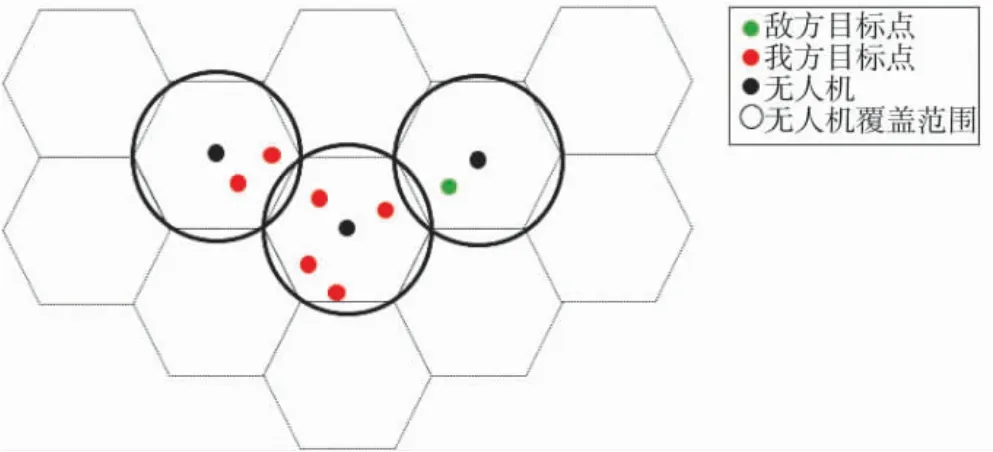
图2 栅格化地图中目标覆盖示意图Fig.2 Schematic representation of targets coverage in a rasterized map

为了聚焦研究问题,本文作出如下假设：1）无人机具有自主避障功能,因此,不考虑无人机间及与环境障碍物间的碰撞.2）在每一步长中,无人机可以从某个栅格单元位置移动到相邻的6 个栅格单元之一.3）无人机性能良好,不考虑燃料耗尽或无人机自身故障等因素.

2 算法设计

对于给定的目标列表和无人机列表,算法的最终目的是找到一个无冲突的目标与无人机匹配方案,使得无人机群所获收益最大化.如果每个目标分配给不超过一架无人机,则可称为一个没有冲突的目标分配方案.本文所研究的问题是一个较为复杂的目标优化分配与连通保持问题,由于建模不确定性、问题大规模性等因素,模型（1）～模型（5）在实际中很难求解.大部分研究者通过集中式组合优化方法或启发式优化方法来求解,但集中式控制本身存在可扩展性差、抗毁性差等问题.而分布式协商是一种以个体分布式而非某个中心节点集中控制的方法并行计算以提高效率,且有较强的鲁棒性、容错性和可扩展性,通过多轮迭代的方式进行资源优化分配,最终通过协商实现资源一致性分配.因此,本文以分布式协商的方式来求解上述问题.

2.1 CBAA 算法简介

CBAA 算法是一种去中心化的拍卖方法,即不需要拍卖师即可解决冲突.算法由两阶段组成,第1 阶段是拍卖过程,每架无人机以异步方式对目标进行投标并得到中标列表,该过程是为了获取有效的目标列表；第2 阶段是协商一致过程,无人机利用协商一致的策略来对中标列表中的目标进行无冲突分配.

2.2 局部划分定义

考虑到无人机只能与其通信范围内的无人机通信,本文将无人机i 及其邻居Ni视为一个局部,并表示为,这种局部的划分方式使得各个局部之间互有交集.假如初始时刻全局通信连通,如果所有局部通信在任意相邻时刻均连通,那么全局通信在任意时刻也将实现连通[23].因此,在本文的分布式控制下,多无人机的通信连通将由各个局部的通信连通保持来共同实现.

2.3 分布式协商目标分配方案架构设计

在多无人机系统中,由于每架无人机的邻居数量以及通信距离有限,在分布式控制下,让无人机群实现某种行为或资源分配的一致性尤为困难[24-26].结合本文研究问题的任务需求,设计一个合理有效的分布式控制架构,并基于此架构进一步设计分布式协商目标分配与连通保持算法.

图3展示了多无人机分布式协商目标分配方案整体构架,算法将通过底层分布式局部协商的方式,来获取无冲突的全局目标优化分配方案.然而无冲突的全局目标分配方案要求各局部内以及各局部间都不存在目标分配冲突,因此,需要局部内和局部间均进行协商以实现无冲突的目标优化分配.

由于本文的局部划分方式使得局部之间互有交集,故局部间协商问题可隐含于局部之间的信息交集中,因此,仅考虑局部内协商即可.以图3中虚线所圈出的无人机子群为例,其中,包含7 个局部{l1,l2,l3,l4,l5,l6,l7,l8},当7 个局部均实现无冲突目标分配时,虚线中的所有无人机将得到一个无冲突的目标分配方案.例如,局部l2={v1,v2,v3,v4,v5}和l5={v2,v4,v5,v7,v8}拥有共同的无人机{v2,v4,v5},当局部l2和l5分别实现无冲突目标分配时,无人机{v2,v4,v5}的目标分配在局部l2和l5中均无冲突,从而使得局部l2和l5之间的目标分配无冲突.当所有局部内均实现无冲突的目标分配时,即可得到全局无冲突的目标分配方案.

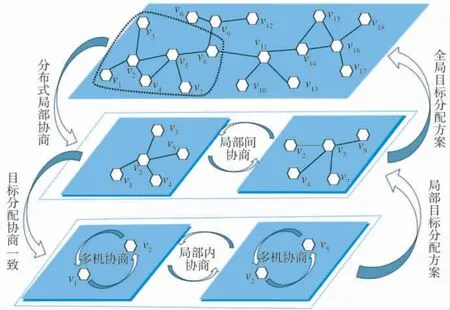
图3 分布式协商目标分配方案架构Fig.3 Target allocation framework under distributed negotiation

因此,本文主要针对局部li内无人机之间的分布式协商目标分配算法进行设计,以保证通信连通性的同时实现目标优化分配覆盖,具体算法设计将在下一节中详细介绍.

2.4 分布式协商目标分配与连通保持算法设计

如图4所示,算法以无人机对地面目标的探测信息作为输入.为了解决目标类型不同以及无人机覆盖能力有限问题,基于无人机的覆盖能力对原始目标M进行分组并得到新目标.接着在拍卖阶段对新目标进行收益评估,并得到目标中标列表Mi.在目标协商一致及连通保持阶段,无人机分别选取中标列表中对自身收益最大的目标,并对产生冲突的目标进行协商分配,接着对目标所在位置进行通信连通性判断,以确定无人机前往覆盖目标的可行性.当局部li中无人机i 分别与其他无人机完成协商后,局部li即可得到无冲突的目标优化分配方案.

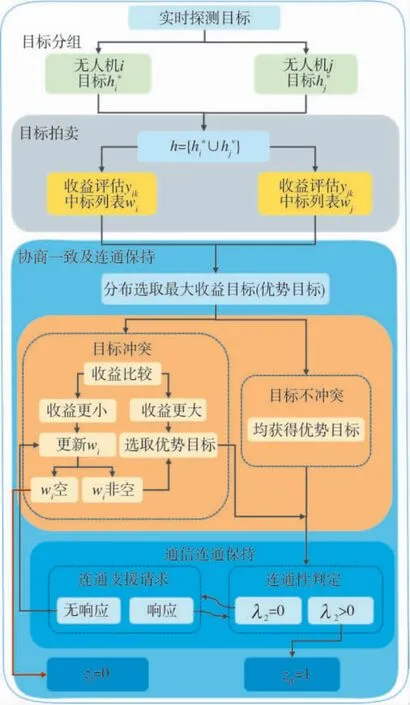
图4 分布式局部协商目标分配与连通保持算法流程Fig.4 Algorithm flow of target allocation and connectivity preservation for distributed local negotiation

2.4.1 目标分组

由于无人机同时只能覆盖一类目标且覆盖数量有限,当同一栅格中存在较多目标且类型不同时,无人机对栅格中的目标收益评估将成为一个较为复杂的过程.为了简化这一过程,定义无人机i 在探测并更新目标信息过程中需维护的目标集合,其中,为无人机对目标分类并分组处理得到的新目标子集,同时目标子集hk中仅包含一类目标,且每个子集所包含目标数量不超过无人机的覆盖能力c.由于无人机的位置坐标为六边形栅格中心,且无人机正好可以完全覆盖所在六边形栅格区域,因此,将目标子集hk所在的六边形栅格中心位置坐标视为目标子集hk的位置坐标,以降低无人机对目标收益估计的复杂度.

以图5为例对目标分组过程作进一步说明.图中正六边形内的目标集合为,假设无人机的覆盖能力c=3,通过以下规则对目标进行分类并分组：

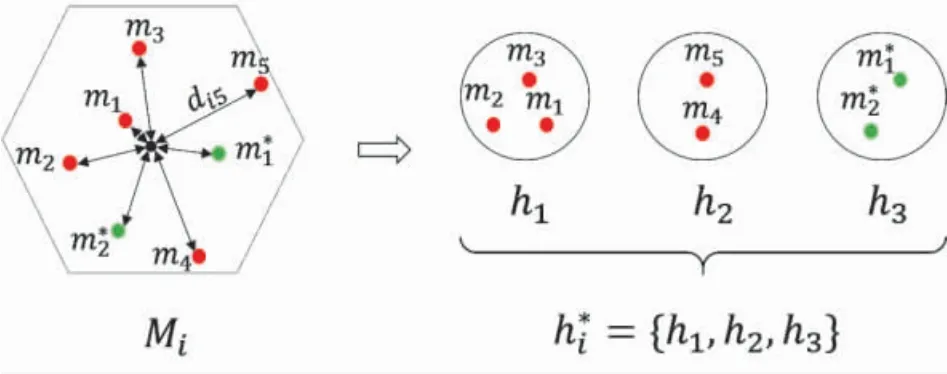
图5 目标分组示意图Fig.5 Schematic representation of grouping targets

2）在同一类型目标集合中,依次选取距离栅格中心最近的目标,每c 个目标分组为一个目标子集hk（剩余不足c 个的分为一组）,得到新的目标集合,其中我方目标子集、,敌方目标子集.

根据以上分组规则,每架无人机对探测到栅格中的目标进行分组得到目标集合,各目标价值向量为,其中,对应目标子集hk的价值,根据目标类型权重以及hk所含有目标数量wk的不同,得到sk的值为：

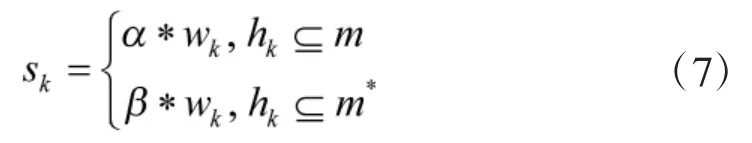
通过对目标的分组,将多个目标分配给一架无人机的问题转化为单个目标子集分配给一架无人机的问题,简化了无人机分布式协商目标分配的复杂度.为了方便,文中所提到的目标均表示分组后的目标子集hk,即以目标子集hk视为目标进行分配.

2.4.2 目标分组如图4中,在目标拍卖阶段,无人机i 与局部li内的其余无人机j 共享目标并得到目标集合.无人机在获得目标信息后,分别对目标进行收益评估并投标,将无人机i 与目标hk的距离dik以及目标hk的价值sk作为无人机当前的收益评估因子,并定义收益函数为：

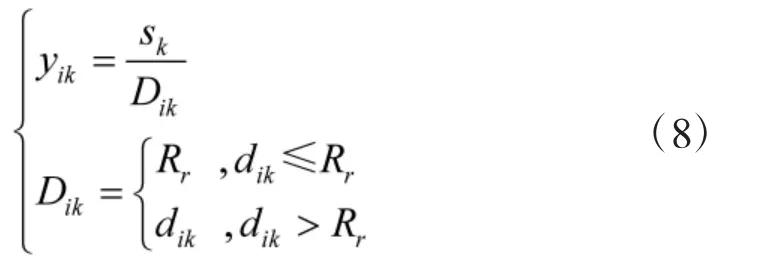
式中,yik为目标hk对无人机i 的收益大小,并以收益大小作为对目标的出价进行投标.其中,1/Dik表示目标k 对无人机i 的距离优势,当目标与无人机同时存在于一个六边形栅格中时,目标已被覆盖,此时距离优势将保持最大值；当目标存在于其他六边形栅格时,无人机距离目标越近则距离优势越大,对应收益也随之增大.定义每架无人机在整个分配过程中储存和更新的两个列表为zi和wi,其中,是无人机i 的覆盖目标列表,表示无人机i 分配到覆盖目标hk,否则zik=0；是无人机i 维护的目标中标列表,假设无人机当前执行任务的收益为,当覆盖目标hk带来的收益yik大于时,视目标hk中标并设置wik=1,反之wik=0.注意,中标的目标被放入中标列表时,列表将以收益从大到小进行排列更新,以便在协商过程中快速分配目标.

2.4.3 协商一致及连通保持

在这一阶段,无人机首先从自身中标列表中选择收益最大的目标,再进行下一步的协商以及连通性判定,无人机仅当分配到不破坏连通性的目标时,才可执行覆盖目标任务.

1）协商一致

各无人机首先采用贪婪策略选择自身中标列表中收益最大的目标,将其定义为自身的优势目标,如图4中,算法在协商一致阶段的迭代中,无人机i 从邻居通信信息中获取到所有邻居的优势目标,若与自身的优势目标不相同,则目标分配无冲突,无人机i可获得自身的优势目标,即zik=1；相反,若与邻居优势目标相同,则目标分配发生冲突,此时,若其他无人机有更高的收益,无人机i 将选择放弃当前优势目标并将该目标从中标列表中清除,再从中标列表中选择一个收益最大的目标作为优势目标.确定优势目标后,无人机针对优势目标所在位置进行下一步的连通性判定工作.

2）通信连通保持

文中无人机i 已知局部li中其余无人机的位置信息,这为无人机i 提供了所使用的局部网络结构.无人机i 通过对局部图的连通性判断,进而对连通性具有破坏性的动作进行约束,从而实现网络的连通保持.

以无人机i 为例,具体连通保持的算法流程设计如图6所示.

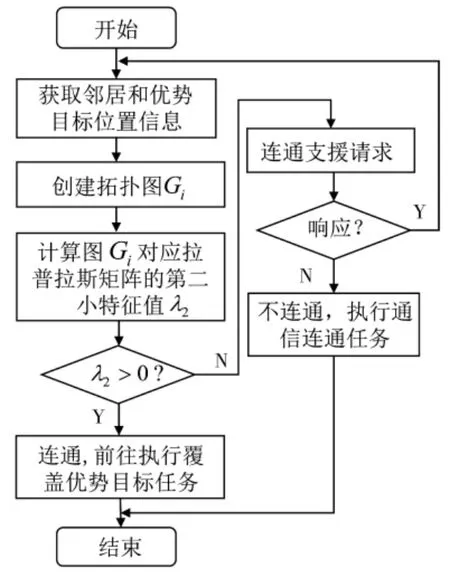
图6 连通保持算法流程图Fig.6 Flowchart of connectivity preservation algorithm

由算法设计可知,无人机i 在协商一致阶段确定优势目标后,以优势目标所在位置坐标为自身下一步的移动位置,并以此坐标结合所有邻居的位置坐标创建拓扑图Gi,求解其拉普拉斯矩阵L 的第二小特征值,进而预估覆盖该目标后通信网络的连通性.若＞0,则表示无人机i 前往并覆盖优势目标的过程中均可保持通信连通,可以对优势目标执行覆盖任务,从而将该目标分配给无人机i,即zik=1；反之,若=0,则表示无人机i 移动后将不能保持通信连通.为了使无人机尽可能覆盖到更多目标,本文加入了连通支援机制,因此,无人机i 在判定通信不连通后向局部li内其他无覆盖目标的无人机发出连通支援请求.

收到连通支援请求的无人机j 以发出支援请求的无人机i 的位置为目标位置,通过连通保持算法对拓扑图Gj的连通性进行判定,若图的拉普拉斯矩阵对应第二小特征值＞0 时,无人机j 可保持通信连通的条件下给无人机i 提供连通支援.获得连通支援后,无人机i 将再次对优势目标进行连通性判定,若能实现连通,则无人机i 将获得优势目标并进行覆盖.如果仍不能保持连通,无人机i 将放弃当前优势目标,再次从中标列表中选择新的优势目标并进行通信连通性判定,循环迭代直到获得可覆盖目标或者所有目标均不可前往覆盖为止.最终没有被分配到目标的无人机i 将作为中继无人机执行通信连通任务,以保持通信网络连通.

通过以上协商过程,即可实现局部内的无冲突目标优化分配和连通保持.在分布式控制下,各个局部以异步方式进行协商分配,从而实现无冲突的全局目标优化覆盖和通信连通保持.

3 仿真与结果分析

本节从不同角度对算法的有效性与通用性进行仿真验证.设置一定数量的无人机,分别在不同目标数量、不同目标移动方式、无人机不同覆盖能力以及两类目标不同价值权重等多种场景下进行实验.每类场景分别以不同随机种子进行3 次实验,每次实验进行100 步,并将3 次实验得到的目标覆盖率取平均值作为当前场景下的目标覆盖率.选取当前场景所有实验过程中无人机通信网络连接的最小连通度min（）作为全局连通性的评判标准,min（）＞0 表明实验所进行的每一步均实现了全局连通.由此,实验采用无人机群对目标的覆盖率以及最小连通度min（）作为指标,来验证算法的有效性.

3.1 实验环境设置

考虑在10×10 平方单位的二维环境中,随机生成M 个动态目标,其中,有m 个我方目标和m*个敌方目标,相应目标类型的价值权重为α、β.实验中可用的无人机数量设为n=30 架,所有无人机拥有相同的配置：覆盖半径Rr=0.5,探测半径Rd=1.0,最大通信半径Rc=2.0,覆盖能力为c 个目标.在每个时间步长中,目标移动速度为0.05.在每次实验的初始时刻,无人机群的初始通信网络被设置为连通,并且使得尽可能多的目标M 在无人机群的覆盖范围内.

3.2 实验过程与结果分析

为验证无人机群在算法控制下的协同多目标覆盖性能,设置在地图中随机生成M=25 个目标,其中,我方目标数量m=12,敌方目标数量m*=13,两类目标价值权重为α=β,无人机的覆盖能力c=1.所有目标的移动方式为直线运动且逐渐聚集于某一空间范围中,实验进行100 步,其中,4 步的目标覆盖情况如图7所示.

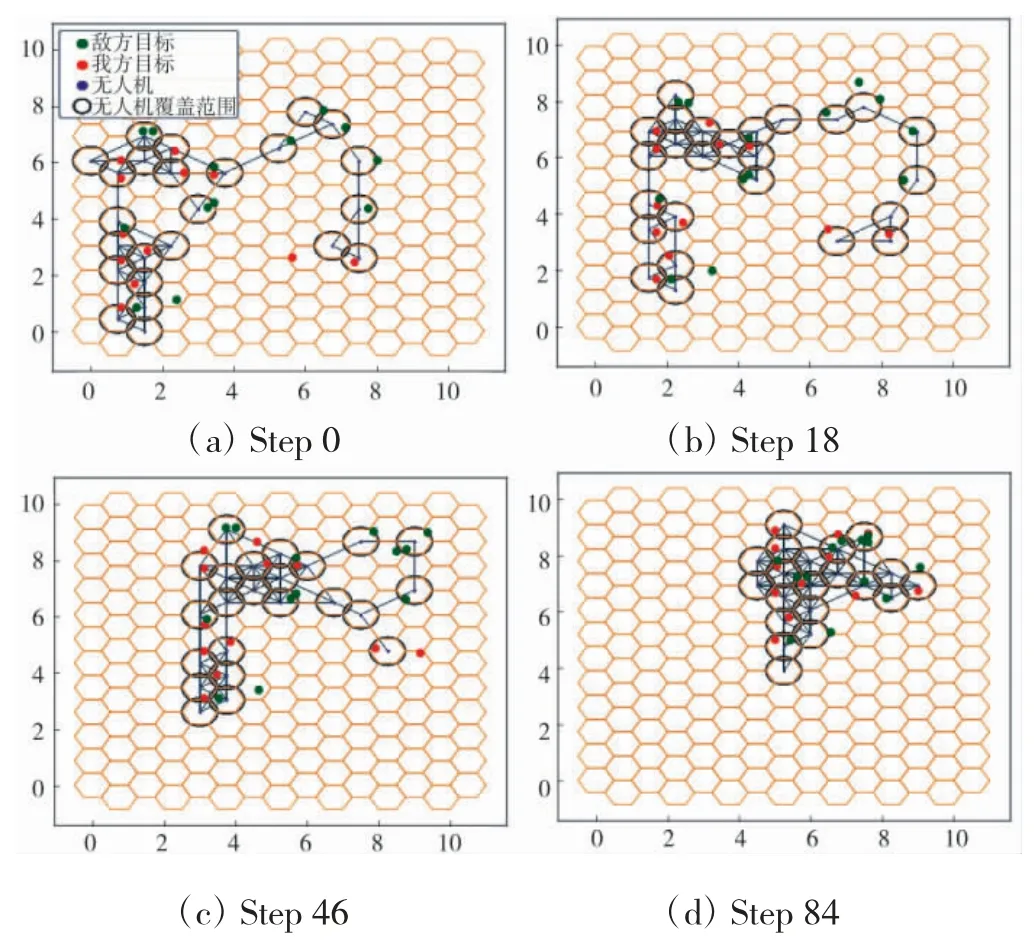
图7 动态目标覆盖Fig.7 Dynamic targets coverage

由图7（a）可知,无人机群在初始状态下通信连通且少量目标在覆盖范围外,在随后的目标移动过程中,需要无人机实时探测获取目标信息,从而进行协商覆盖.从图7中可以直观地看到,无人机群随着目标的移动而灵活变换通信拓扑网络,这是由于当无人机发现更高价值目标后,可通过连通判断、发出连通请求等多种机制,实现多无人机的协同移动.通过以上分析得知,本文提出的分布式协商目标分配算法可以使无人机群拥有良好的协同覆盖性能.

在下一组实验中,为了验证算法在不同目标优先级分配下的有效性,基于目标直线移动实验,设置两类目标的价值权重关系分别为α＞β 和α＜β,并在不同目标数量M 下进行实验测试,其中,不同类型的目标数量m=m*.实验得到不同价值权重下目标平均覆盖率以及实验中的最小连通度min（）如表1所示.

表1 不同目标价值权重下的覆盖性能测试Table 1 Coverage performance test under different target value weights

从表1中可以直观得知,随着目标数量的增加,算法性能指标趋于下降,即目标的覆盖率逐渐降低,这是因为在有限的无人机数量下,算法为了保持通信网络的连通而选择放弃部分目标,这同时也说明了算法在通信连通保持方面的有效性.此外,当目标m*的权重较大时（α＞β）,无人机对目标m*的覆盖率高于对目标m 的覆盖率,且随着目标数量的增加,覆盖率的差距逐渐增大,这是因为目标的增加使得无人机有了更多的目标选择,从而分配更大收益的目标m*执行覆盖目标.同理,当α＜β 时也有类似的测试效果.上述分析表明,所提出的算法在目标具有不同优先级的条件下具有较好的覆盖性能,同时在不同的动态目标数量场景下具有很好的泛化性能.

最后,设置了不同的动态目标数量分别以不同的方式移动,并分别测试无人机在不同的覆盖能力c=1和c=5 下对目标的覆盖性能,其中,设置α=β,目标的移动方式为直线移动以及随机移动两种,测试结果如表2所示.

由表2可知,对于无人机的覆盖能力c=1 而言,随着目标数量的增加,目标的覆盖率相对于覆盖能力c=5 时的差距逐渐增加,这是因为覆盖能力更大时,相同数量的无人机可以覆盖更多的目标,从而使得在面临较大数量的目标时,无人机覆盖能力越大则总覆盖率越高.此外,当目标数量较少时,将有足够的无人机前往覆盖目标,即有多个目标处于同一栅格中时,算法将分配多架无人机前往同一栅格覆盖不同目标,因此,在目标数量较少的情况下,即使单架无人机覆盖能力较低,也将有较好的覆盖性能.

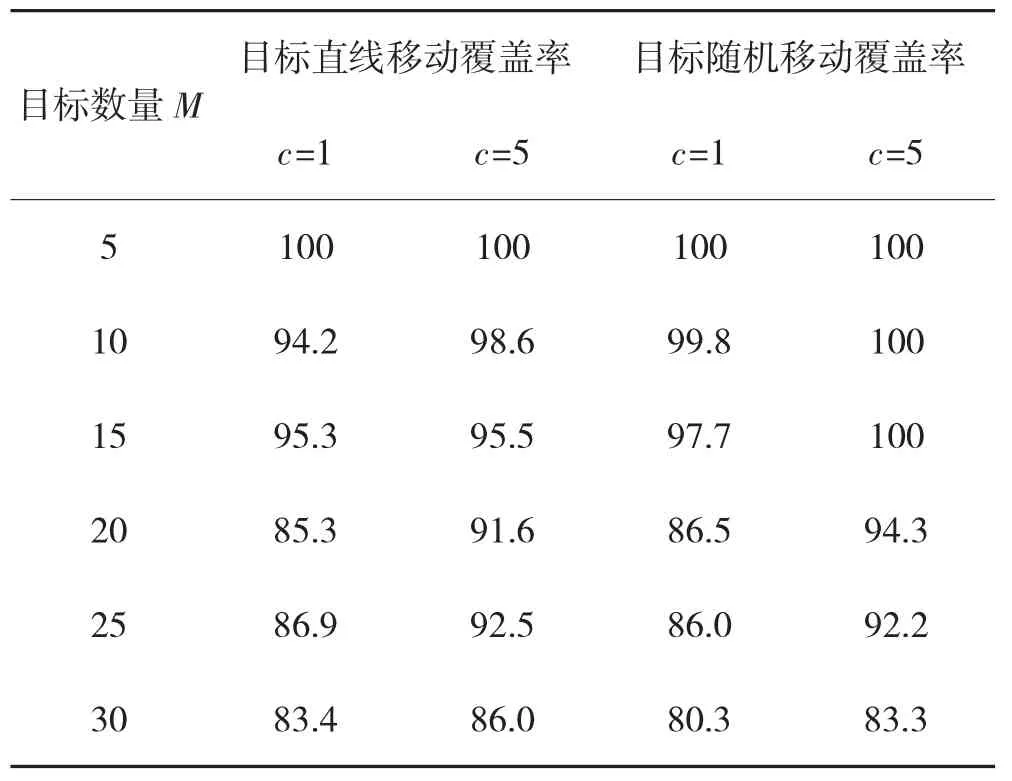
表2 不同覆盖能力下的覆盖性能测试Table 2 Coverage performance test under different coverage capabilities

4 结论

本文提出了一种基于分布式协商的多无人机目标覆盖与连通保持算法,以解决多无人机动态多目标覆盖与通信连通保持问题.实验结果表明,本文提出的分布式协商算法,可以综合考虑无人机的覆盖能力、目标类型、目标覆盖优先级以及通信连通保持多种因素,使得多无人机可以在分布式控制下,在动态环境中实现目标优化覆盖和通信连通保持.