基于超单元理论的焊接疲劳分析

陈 瑜，龚益玲

（上汽大众汽车有限公司 产品研发车身开发部，上海 201805）

随着汽车行业的飞速发展，汽车驾驶性能、安全性能和舒适性能的要求也在不断提高。汽车企业依据法规要求和相应的标准，对汽车的质量和乘用体验不断改善。汽车的行李箱盖作为汽车十分重要的功能部件，具有隔绝噪声、缓冲来自外部冲击的作用。在车辆的使用过程中行李箱盖反复开启和关闭，承受循环力加载和卸载，行李箱盖与密封条的疲劳寿命直接关系到车辆的经济性和乘坐舒适性。由于造型和冲压工艺的需求，在车辆行李箱盖设计中，通常将外板设计成分体式结构，再通过激光焊将上下板连接成一体。这样的设计兼顾工艺及造型，所以在很多车型上得到了广泛应用。但在分体式行李箱盖的开关耐久试验中，上下钣金连接处的激光焊出现激光焊耐久开裂的风险相对比较大。

不同部位的激光焊缝承受不同的应力载荷，一旦某些部位的激光焊工艺质量存在缺陷，就会导致局部焊接强度大幅度降低，进而引发低周期的激光焊开裂现象。此外，结构强度也是影响激光焊开裂的关键因素。车辆行李箱盖关闭是一个瞬态过程，在密封条、缓冲块及锁的作用下，车辆的行李箱盖外板钣金在惯性作用下周期性地对激光焊施加疲劳载荷。如果结构设计未考虑结构强度对激光焊的承载极限的影响，激光焊同样会出现低周期的开裂现象。

疲劳试验周期长，耗费企业巨大的开发成本及时间成本。现有的行李箱盖疲劳仿真技术中，存在着诸多简化和缺陷：首先，行李箱盖钣金件在疲劳模型中简化为壳单元，激光焊缝定义为六面体单元，而钣金和激光焊缝连接处使用刚性连接，因此，无法准确模拟钣金连接区域受力状况以及疲劳开裂问题。其次，在疲劳模型中，安装在车辆车身止口的密封条由高粘弹性材料制成，传统疲劳模型只是简单地将其简化成线性的弹簧单元，无法准确反映密封条在实际开闭行李箱盖过程中的瞬态材料特性；最后，作为行李箱盖开闭过程中传递力的重要零部件，密封条和车身止口之间存在复杂的接触关系，也是需要考虑的因素。因此，在行李箱盖疲劳分析有限元模型中，激光焊缝和密封条的受压特性及接触关系的定义，对于行李箱盖钣金受力的大小和疲劳寿命也有着重要的影响。

本文针对某款车型典型的分体式内外板行李箱盖激光焊开裂问题，基于超单元理论，建立用于激光焊的精细化模型，对临近裂纹尖端区域进行有限元网格细化；通过二维压缩模型对密封条进行非线性材料属性标定及相关接触定义，模拟车辆密封条在高应变率下非线性的动态性能，搭建行李箱盖疲劳有限元仿真模型，最后通过相应的试验验证等进行一系列的疲劳研究。

1 基于超单元理论的激光焊有限元模型

在建立传统激光焊有限元模型时，行李箱盖钣金件常简化为壳单元。钣金和激光焊连接处使用刚性连接，因此，无法准确模拟钣金连接区域的受力状况；如果对整个行李箱盖及所有钣金连接处使用超细化模型，整体模型有限元网格数目会增加500～1000倍，虽然能准确模拟钣金及其连接处的受力及失效情况，但是模型巨大，因此计算效率极其低下。

1.1 超单元理论

超单元是一种基于疲劳断裂理论的超细化聚合单元，同时考虑实际焊接结构连接形式和结果复杂程度的巨型单元。在实际仿真模型中，焊点或者焊接单元被简化为普通的四面体或者六面体单元，焊接边缘节点使用刚性连接与主模型进行耦合。这种单元只是焊点的表示形式，进入到平衡迭代方程的矩阵则是超单元的聚合刚度矩阵。如图1(a)所示为最终模型焊点表现形式，图1(b)所示为实际超单元表现形式。

图1 焊点的超单元表现形式

熔化极惰性气体保护焊、熔化极活性气体保护电弧焊和激光焊等焊接方式作为车身板件中的焊线常用经济有效的焊接技术，与点焊一样，疲劳强度评估是基于焊缝根部的计算张力。超单元模型采用单元模型的裂纹尖端半径=0.05 mm，网格与点焊模型网格类似，如图2所示。

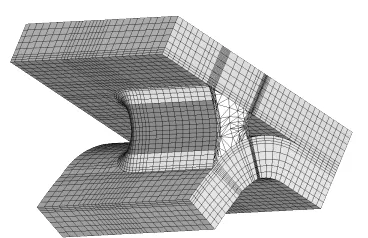
图2 激光焊缝的超单元表现形式

1.2 裂纹尖端

接头的抗拉强度取决于接头之间切口的应力张量大小，这些应力张量取决于切口的形状和尺寸。在裂纹尖端处应力和应变的梯度很大，因此，临近裂纹尖端区域的有限元网格有必要进行细化。如图3所示，真实的缺口被一个更大曲率的角膜缘似的单元过渡代替。对于车身中的薄板（0.6～3 mm），虚拟切口设定为弯曲半径为0.05 mm。

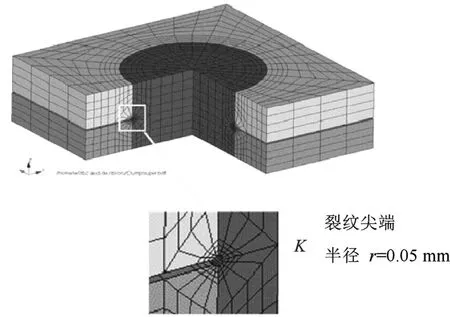
图3 裂纹尖端网格细化

1.3 超单元刚度矩阵转换

在有限元计算结果中，计算局部坐标系下的应变，须将焊接单元的全局位移转换到局部坐标系中。此后，确定局部刚性以及由该局部刚度引起的变化，并从总刚度中删除。随后，节点力可以通过将修正后的局部坐标系下位移与局部坐标系下刚度矩阵相乘，并添加到先前的荷载增量来计算。有限元计算过程中，需要将刚度矩阵和节点力转化为新的全局坐标系下坐标值，并返回到全局计算过程中。

全局坐标系由8节点设置定义。局部坐标系中定义的刚度矩阵根据全局坐标系进行变换，如图4所示。Fortran用户子程序的编程方式使焊接点也能在几何非线性计算中经历较大的刚体旋转。

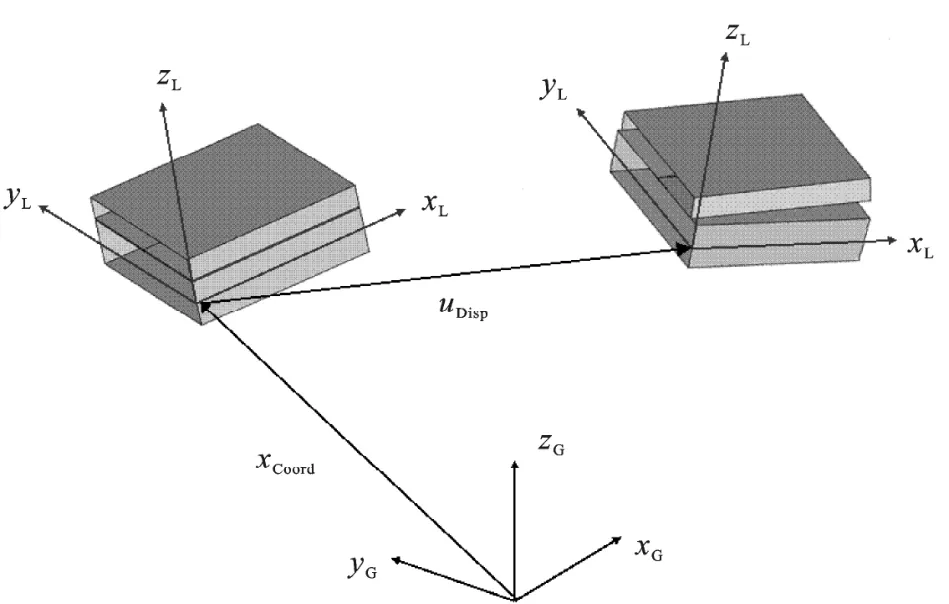
图4 全局坐标转换

1.4 总体刚度矩阵变化

通过超单元建模得到连接区域的局部细化模型后，通过计算可以得到修正的焊接区域的刚度矩阵，将此刚度矩阵应用于疲劳计算的有限元模型中，保证计算效率的前提下，大大提高了计算精度，准确模拟出钣金件连接处受力情况及疲劳开裂的风险。

设连接区域局部细化模型含有个单元，其整体结构的刚度方程可表示为

对于每一个体单元，单元节点数为8，单个节点有3个自由度，刚度方程表示为

其中，[]为第个体单元刚度矩阵；=1,2,3…；{}可表示为

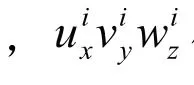
此可以得到第个体单元的刚度矩阵，由式（4）表示：

2 疲劳S-N曲线分析

实验样件在不同方向角度的拉伸载荷加载、不同厚度的样件情况，其S-N曲线基本是一致的。考虑到有限元模型计算输出的结果为应力值，实际使用的S-N曲线应为应力与疲劳循环次数的曲线。在曲线转化过程中，综合焊接点的有限元模型，将试验力转换为名义结构应力。包括头部拉力试验和剪切试验，由这些理论计算值与S-N曲线组成新的能够在工程中应用的S-N曲线。

图5为试验样件进行100 000次循环疲劳试验循环加载后的失效状态，图6为焊接样件疲劳有限元模拟。通过综合焊接点模型，将试验力转换为名义结构应力。在工程应用中，由于焊接区域存在复杂的几何结构和荷载条件，从来没有纯粹的头部拉力或剪切，结构受到的总是混合荷载类型，不变性对于实际构件的适用性尤其重要。本文中名义结构应力为局部应力，没有考虑缺口效应的叠加。

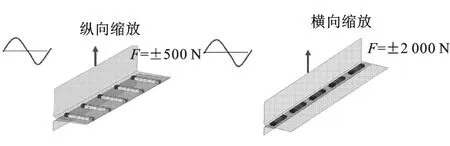
图5 焊接样件100 000次循环疲劳试验

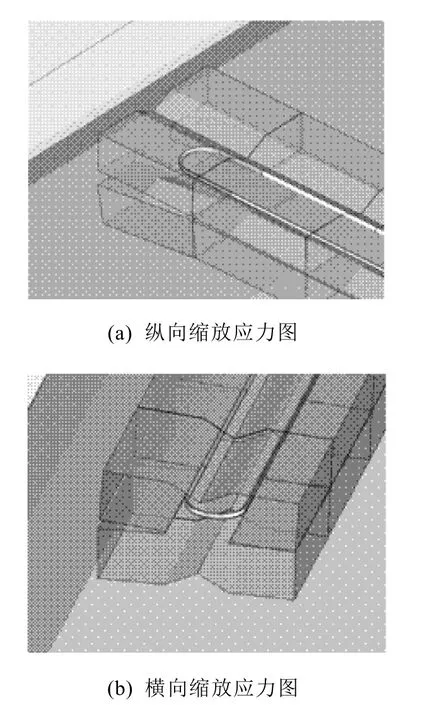
图6 焊接样件疲劳有限元模拟

试验中使用焊接的样件进行应力拉伸试验，并依据下列公式计算得到名义结构应力：

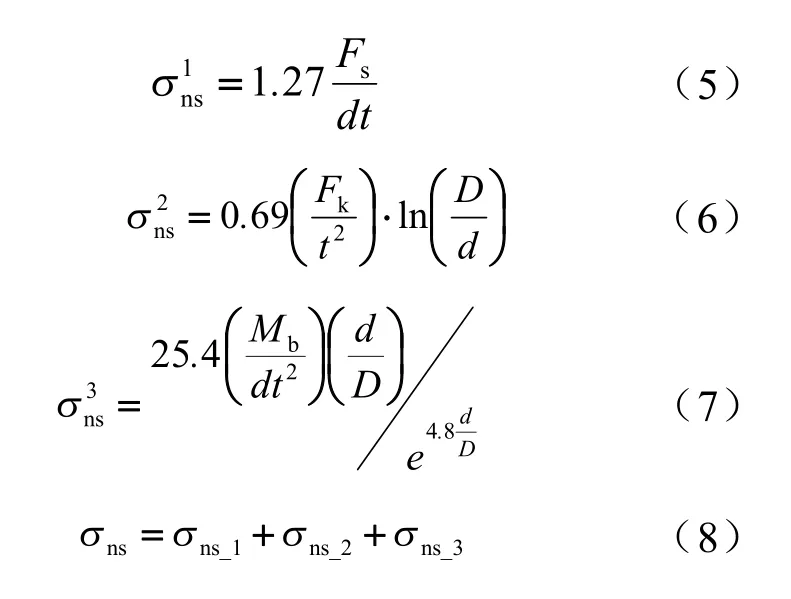
式中，为剪切应力；为头部剪切应力；为剥离应力；为名义结构应力；为剪力；为头部剪力；为弯曲力矩；为焊点直径；为焊点连接钣金的厚度；为钣金焊点影响区域直径。

3 行李箱盖耐久疲劳物理台架试验

图7为行李箱盖开闭耐久疲劳物理试验台架。试验将带有内饰的完整行李箱盖系统安装在固定的整车骨架上，外置牵引系统控制行李箱盖以恒定的速度进行多次关闭。传统的行李箱盖开闭耐久疲劳物理试验台架多使用气泵式牵引系统，由于其无法精确控制关闭速度，本文所述的试验均采用电动牵引系统。测速仪放置于行李箱盖下边缘，用以准确记录每次试验的关闭速度。

图7 行李箱盖开闭耐久疲劳物理试验台架

4 行李箱盖耐久疲劳数值仿真

4.1 行李箱盖有限元模型

根据行李箱盖疲劳耐久物理试验，搭建行李箱盖疲劳分析有限元模型，如图8所示。其中气弹簧以及行李箱盖的缓冲块简化为带参数的Connector单元。

图8 行李箱盖疲劳分析有限元模型示意图

根据设计测量的数据重心，对于后尾灯以及后行李箱盖内饰、雨刮电机等进行简化处理，以集中质量的形式通过Coupling函数与钣金连接，如图9所示。

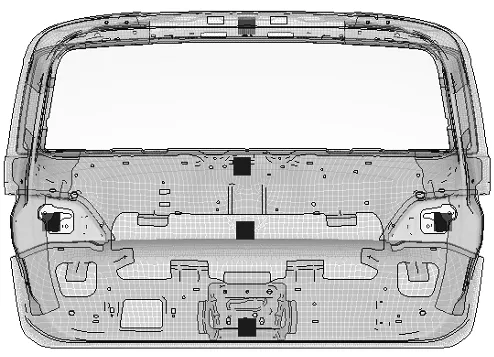
图9 行李箱盖内饰、尾灯等集中质量布置示意图

4.2 密封条模型

4.2.1 传统密封条有限元模型

在车辆行李箱盖疲劳传统的仿真技术中，对密封条采用不同的处理方法会对结果产生不同的影响。通常，密封条简化为受力方向垂直于钣金平面的具有均匀刚度的线性弹簧单元。以往的疲劳分析中，密封条定义为线弹性，其刚度系数通过式（9）计算得出：

式中，垂直于卡槽加载力=200 N，为密封条压缩量，如图10所示。

图10 行李箱密封条传统压缩性能图

4.2.2 密封条平面应变单元模型

由于行李箱盖在关闭瞬间是高非线性的瞬态过程，因此，具有恒定刚度的线性弹簧单元无法准确反映该过程中行李箱盖与密封条连接区域的非线性关系。

基于ABAQUS有限元计算软件建立行李箱盖疲劳分析的密封条模型，如图11所示。密封条沿着安装路径的扫掠曲线建立一系列间隔为10 mm，长度为10 mm的等距的Connector单元，Connector单元指向为密封条安装区域中，密封条密封接触点和密封条安装点的连线。所组装建立后盖疲劳计算模型中，钣金模型与密封条模型之间通过共用节点的方式连接。

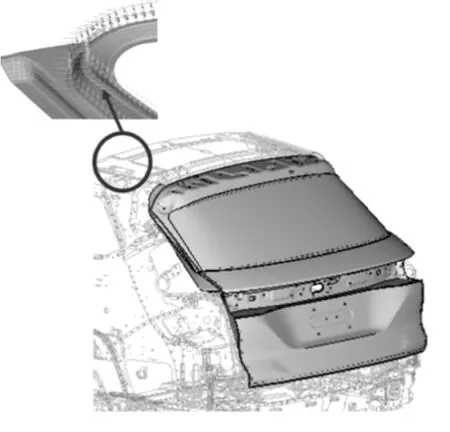
图11 行李箱密封条有限元示意图

所建立的密封条有限元模型被赋以Connector单元材料参数，材料属性通过密封条不同分区的二维截面模型获得。

4.2.3 密封条二维截面模型

沿密封条安装路径提取密封条安装曲线，并根据安装曲线的曲率进行分区，如图12所示，不同的分区能够反映不同安装区域的开闭件及车身的钣金截面和密封条的相对位置，不同分区对于密封条的压缩量以及压缩方向都是不同的。图13示意了分区和分区的截面对比图，图中很明显地展示了两个不同分区在后盖关闭工况中对于密封条的压缩方向的差异。

图12 后盖密封条分区示意图

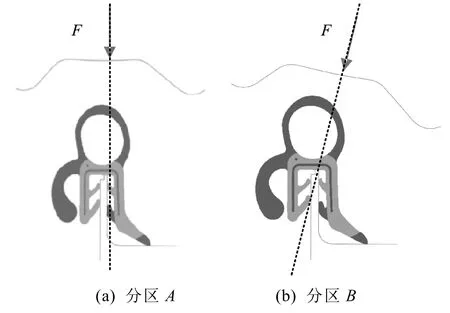
图13 后盖密封条二维截面不同分区对比图

由于每个分区的密封条压缩边界条件不同，需要对每个分区建立独立的密封条压缩模型进行压缩仿真分析。图14示意了分区密封条压缩模型，边界条件和加载方式为约束车身侧卡槽，对于加载面施加一个绕行李箱盖铰链转轴的角速度。此外，各个分区的密封条截面、行李箱盖的加载面、距离铰链轴位置的远近导致每个分区加载面的角速度也各不相同，需要分别逐个建模分析计算，最后得出各个分区密封条的特性曲线，如图15所示。

图14 后盖密封条不同分区压缩模型示意图

图15 力位移曲线

本文提出的数值方法不仅能准确计算出密封条因安装曲率变化造成的截面受力性能变化，同时，还能更加精确地模拟由超粘弹性材料制成的车辆密封条在高应变率下的非线性动态性能开关过程中密封条连接区域的受力状况。

4.3 焊点模型

基于本文第一节介绍的超单元理论，将后盖疲劳关闭模型中激光焊建成超单元，如图16所示，并提前计算其刚度矩阵，用于后续的疲劳关闭分析。

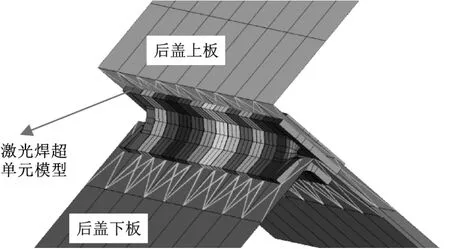
图16 后盖疲劳关闭工况中的激光焊模型示意图

4.4 初始条件加载

根据实际的疲劳试验工况，定义相关的边界条件，如图17所示。铰链处约束除了向转动的其他五个自由度。

图17 后盖疲劳关闭工况初始边界条件示意图

根据企业内部标准，以铰链轴为轴心，沿着关闭方向，施加一个角速度，使后盖下边缘的关闭速度能够达到1.6 m/s。

4.5 疲劳分析

通过Abaqus求解器分析该后盖疲劳关闭模型。通过仿真模拟计算可以得到激光焊端部的应力云纹图（如图18所示）以及激光焊端部的应力曲线图（如图19所示）。

图18 后盖疲劳关闭激光焊应力图

图19 后盖疲劳关闭激光焊端部应力曲线图

根据疲劳模拟计算所得到的激光焊端部应力值曲线（如图19所示），结合疲劳曲线，根据公式（6）—（9），得到疲劳关闭的疲劳次数。其中和分别对应图19中后盖锁一级锁止和二级锁止时刻激光焊端部的应力值。为后盖疲劳工况中，后盖锁一级锁止时刻应力对应的后盖关闭疲劳次数；为后盖疲劳工况中，后盖锁二级锁止时刻应力对应的后盖关闭疲劳次数。最后根据公式（10），得到后盖整个关闭历程的疲劳总次数。

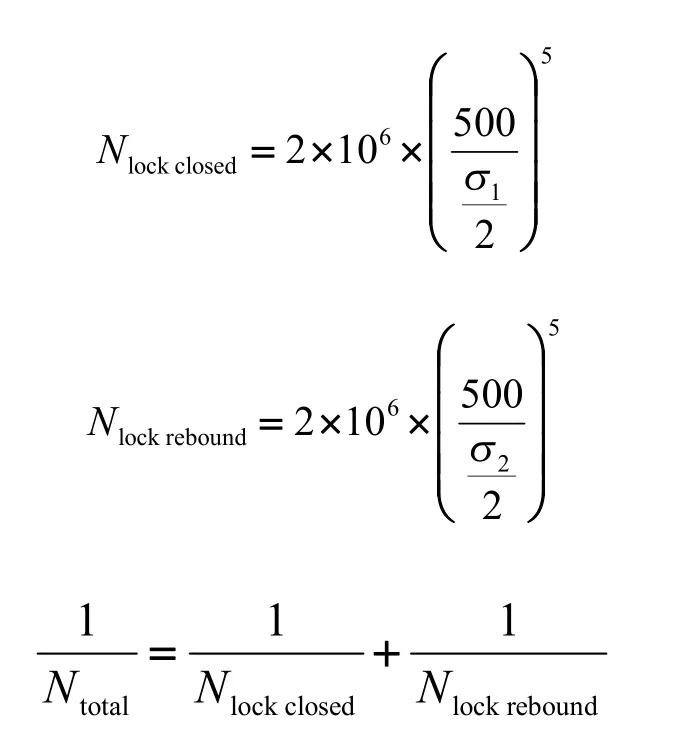
根据后盖疲劳计算分析得到的疲劳次数，可以有针对性地优化后盖结构，提升后盖在疲劳工况下的疲劳寿命。

5 结论

本文针对某款车型典型的尾门激光焊开裂问题，基于超单元理论，建立用于激光焊的精细化模型，对临近裂纹尖端区域的有限元网格进行细化，得到修正的多维度激光焊的刚度矩阵。相比于焊点连接区域初始状态的模型使用8个壳单元和一个实体单元，共26个单元节点数，使用微单元技术对焊点连接区域局部有限元模型进行重构，所使用的超细化焊点连接区域有限元模型使用=6 272个实体单元，共7 380个节点，自由度为7 380×3=22 140，局部模型扩展700倍，能够准确对连接区域的刚度矩阵进行修正。

同时通过二维压缩模型对密封条进行非线性材料属性标定，更准确地模拟车辆密封条在高应变率下的非线性的动态性能，有效提高了车辆尾门激光焊计算效率和疲劳开裂的风险预测精度。

有限元仿真与实验结果的对比显示，使用传统仿真技术的方法连接处使用刚性连接建立，得出钣金连接区域的最大应力值为1 649 MPa，依据S-N曲线得出的疲劳寿命为164 031；通过优化焊接单元以及密封条的建模方法，对疲劳模型的刚度矩阵进行修正后，得出钣金连接区域的最大应力值为1 863 MPa，依据S-N曲线得出的疲劳寿命为89 118；在试验验证中，在第90 000次过程检测时出现了疲劳开裂。通过本文所述的建模方法准确地模拟了钣金在该连接处的受力及失效情况的模拟及对标，能够更加有效地服务于后续车型研发过程结构的改进，在设计阶段就能够对疲劳失效问题提供及时的预警及改正，有效减少了后续实验失败的次数，节约了企业的研发成本。