基于Q-learning的插电式混合动力 汽车能量管理策略
2022-11-02田泽杰
田泽杰
(长安大学 汽车学院,陕西 西安 710064)
插电式混合动力汽车(Plug-in Hybrid Electric Vehicle, PHEV)结合了传统内燃机汽车和纯电动汽车的特点,在当前环境污染和电池技术的限制下成为了最具发展潜力的汽车。由于拥有多个能量源,所以PHEV能量管理策略的开发是影响整车动力性和经济性的核心技术。目前解决能量管理问题的措施有基于规则的方法,如:基于确定性规则和基于模糊控制策略;基于模型优化的方法,如:动态规划和庞特里亚金极值原理。基于模型优化的方法考虑了整个行驶工况,通过数值计算得到全局最优解,但不具备在线应用的可能,只能作为一种对比的手段。
随着人工智能技术的发展,一些智能算法,如:人工神经网络,强化学习等也得以应用于PHEV能量管理策略。强化学习可以不依赖于系统模型,通过智能体和环境的交互产生的奖励信号自主探索和学习到最优策略。本文基于强化学习中具有代表性的Q-learning算法构建了PHEV的能量管理策略,结果表明,此策略可以在有限的步骤中自主学习,并逼近全局最优。
1 整车参数
本文所研究的PHEV为某款串联结构的西安市公交车,整车由两个轮边驱动电机驱动。能量源由动力电池和一款天然气发动机与汽车启动发电一体式电机(Integrated Starter and Generator, ISG)电机集成的辅助动力单元(Auxiliary Power Unit, APU)构成。该款车型整备质量为13 500 kg,轮边主减速器传动比为13.9,电池容量180 Ah,电池包由168个电压为3.2 V的电池串联组成,迎风面积为8 m。其动力传动结构如图1所示。

图1 PHEV动力传动结构
1.1 驱动电机模型
驱动电机可以正转产生驱动力也可以反转进行制动能量回收。对电机进行仿真时,由实验数据进行插值拟合电机效率和电机转速、电机转矩之间对应的关系。

式中,为电机效率;,为电机的转矩和转速。
1.2 APU单元模型
该APU单元与行驶车速不存在机械耦合关系,可以进行独立控制。为简化整车控制难度,首先计算发动机和ISG电机组合供能时的最优燃油消耗曲线,在仿真计算时,仅由功率便可以通过插值得到对应的燃油消耗率。

式中,()为燃油消耗率;(()为APU单元功率。
1.3 电池模型
本文采用包括开路电压和内阻的等效电路模型对电池进行建模,由电池荷电状态(State Of Charge, SOC)插值计算开路电压和电池内阻,对应的SOC状态转移可通过下式计算:

式中,为开路电压;为电池等效内阻;为电池容量;为电池功率。
1.4 需求功率模型
整车需求功率可通过车辆的纵向动力学模型计算,当不考虑坡道阻力时,需求功率为

式中,为需求功率;为滚动阻力功率;为空气阻力功率;为加速阻力功率;为车辆质量;为重力加速度;为滚动阻力系数;为车速;为空气阻力系数;为迎风面积;为车辆旋转质量换算系数;为加速度。
2 基于Q-learning的能量管理策略
强化学习的核心就是指智能体产生动作和环境进行不断的交互,并通过环境实时反馈给智能体的奖励信号,让智能体自主学习在一个环境中的不同状态到行为的映射关系。如图2所示,基于这个映射关系而产生的序列化决策可以最大化奖励信号。

图2 智能体与环境的交互图
强化学习可分为基于表格的传统算法,如Q-learning、Sarsa算法和基于神经网络的深度强化学习算法,如深度Q网络(Deep Q Network, DQN)、深度确定性策略梯度算法(Deep Deter- ministic Policy Gradient, DDPG)算法等。如图2所示,一个标准的Q-learning算法包含智能体、环境、状态、动作、奖励、策略和状态-动作值函数七个基本组成。
Q-learning的关键是建立一个状态-动作价值表(,),存储每一状态下各动作的价值估计。不仅根据这个表来选择动作,并且根据实时的环境反馈以及时序差分算法对该表进行值函数的迭代更新,以期让智能体获得一个最大化未来总奖励期望的策略。Q-learning算法的更新公式如下:
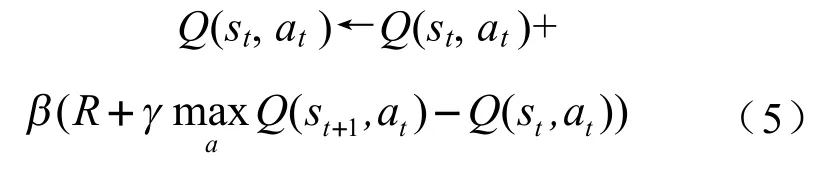
式中,表示学习率,其值越大,算法收敛的速度越快,但是过大容易造成结果的震荡;表示衰减系数,介于0到1之间,用于在当下奖励和未来奖励之间取得平衡,同时也保证了算法的收敛性;为当前状态下的即时回报;(,)为用于映射当前动作到长期总奖励的状态-动作值函数。
本文基于Q-learning算法对插电式混合动力汽车能量管理策略进行求解,目的是降低车辆总能耗,提高PHEV汽车的经济性。选取需求功率和电池SOC作为状态变量,将发动机和ISG电机组成的APU单元提供的功率作为动作变量,则相应的电池应提供的功率为()=()-(),奖励信号是与发动机实时燃油消耗率和当前电池SOC相关的函数。目标函数设定为带有衰减的未来所有状态的累计回报:

该插电式混合动力汽车能量管理的目标是达到最优的经济性,因此,把SOC和发动机瞬时消耗作为即时的反馈,将奖励信号设置如下:
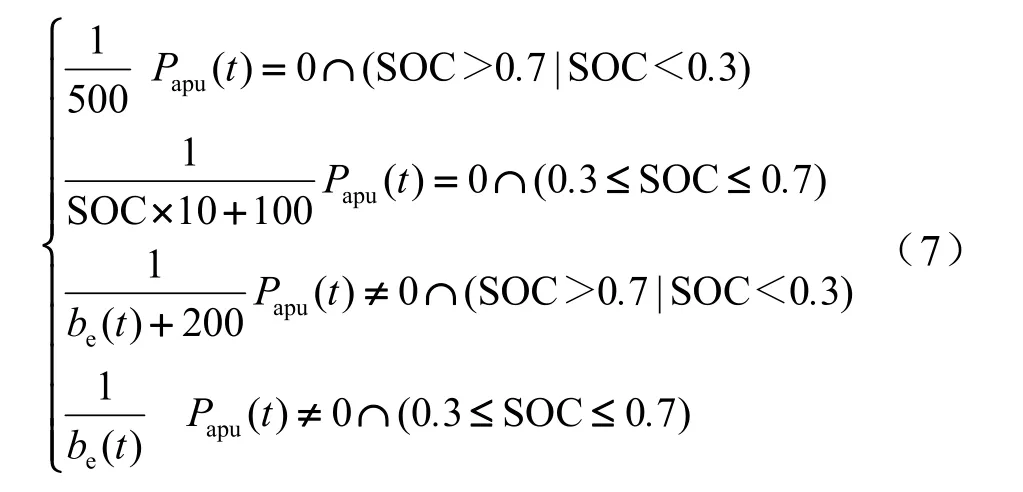
通过奖励信号设置,保证电池的荷电状态在0.3到0.7之间,使智能体在规定边界之内探索并使用更具有经济性的动作。
图3展示了使用Q-learning算法求解该问题的伪代码,其中的episode为一次设定的循环工况。

图3 Q-learning求解过程伪代码
伪代码中,衰减系数取0.9,学习率=1/。选择动作时的-greedy策略如下:

式中,=1/,为一时变的概率,保证在学习初期尽可能多的探索动作,并在学习后期尽可能多的去利用学习到的表。
3 仿真结果
考虑该插电式混合动力汽车的情况,将17次连续的中国典型城市公交循环(Chinese Type City Bus Circle, CCBC)工况作为一个完整的循环,以达到充分利用混合动力汽车的“混动”的优势。首先把状态变量和动作变量离散,生成初始的表,并将每次循环初始SOC设定为0.7,基于状态和表,根据贪婪策略在每一时间步选取动作,并及时更新表中对应的状态-动作值函数。随着表的不断迭代,最终会趋于收敛,设定循环次数N=18 000次。

表1 Q-learning能量管理策略结果
当天然气价格取3.7元/m,电价格为0.8 kWh时,图4为每轮迭代下的循环总价格收敛情况。
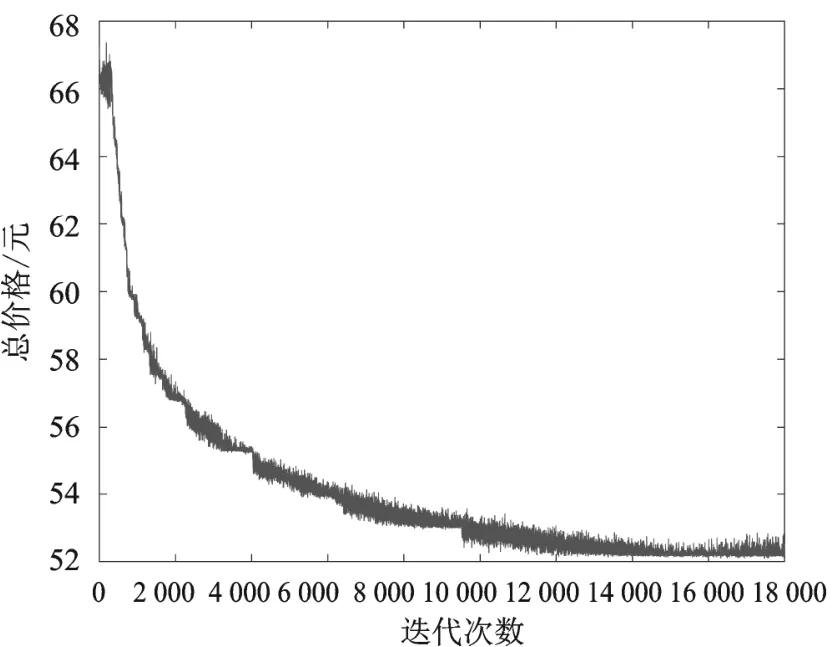
图4 总价格收敛过程
为验证Q-learning算法在插电式混合动力汽车能量管理中的有效性,本文使用基于庞特里亚金极小值原理的方法来计算全局的最优解。从图5中SOC下降的情况可以看出,两种算法在初始SOC均为0.7的条件下,最终SOC都到达了SOC下限0.3。在总行程接近100 km的循环下,基于Q-learning算法的结果只比全局最优算法PMP贵1.57元,证明了基于Q-learning计算策略的有效性。并考虑到PMP算法对于协态变量的选取过于敏感,所以基于Q-learning得到的表策略有更强适用性与鲁棒性。
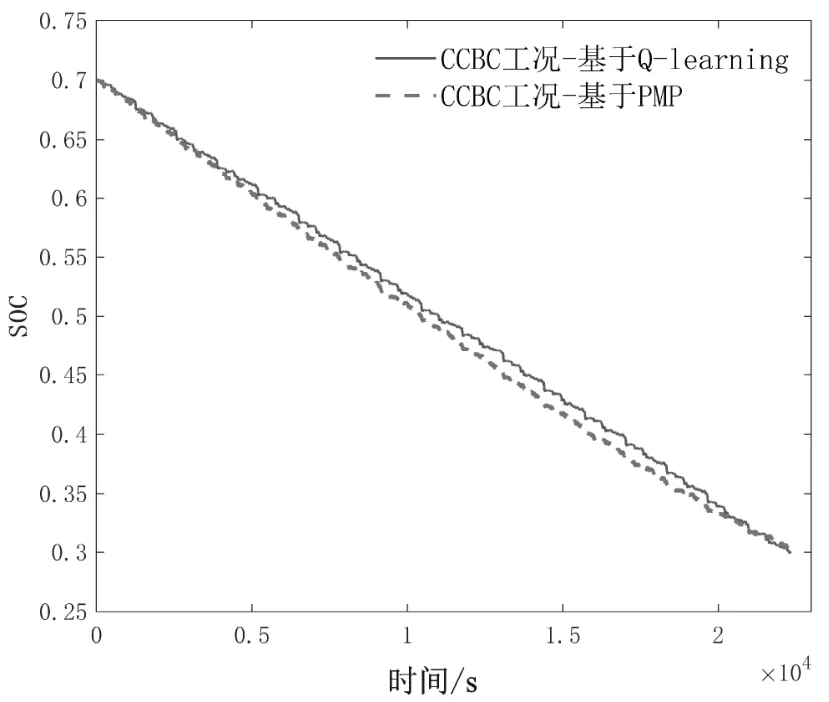
图5 Q-learning/PMP策略SOC下降图
4 结论
本文针对一款串联插电式混合动力汽车,设计一种基于Q-learning的能量管理策略。在连续17次CCBC工况下,相比于全局最优算法PMP,结果仅贵出1.57元,表明了基于Q-learning算法的有效性。
