自动驾驶车辆弯道处换道轨迹规划与跟踪控制
2022-11-02侯宝龙龚柯阳史志飞
侯宝龙,龚柯阳,史志飞
(长安大学 汽车学院,陕西 西安 710064)
近年来关于自动驾驶汽车的规划与控制的研究成为实现自动驾驶的核心点之一。规划模块从整体上分为全局的导航规划与局部的路径规划,局部的路径规划也称为局部的轨迹规划。局部轨迹规划多采用直接构造法,例如直线圆弧段构造、多项式曲线法、样条曲线插值法等。轨迹的跟踪控制阶段便是控制车辆沿着路径规划层的路径行驶,同时在保证操纵安全和平稳的前提下尽量减少跟踪偏差。常用的跟踪方法有纯跟踪法、Stanley法、比例-积分-微分法、模型预测控制(Model Predictive Control, MPC)法。弯道路况相比直线道路的规划更加复杂,不仅需要轨迹的曲率连续性来保证传至人体的加速度变化,从而保证舒适性,还需要考虑换道过程中的动态障碍物,从而确保安全性。本文从智能车辆的规划与跟踪控制算法出发,重点研究弯道处变道过程的轨迹规划与轨迹跟踪控制。
1 引入Frenet坐标系
1.1 笛卡尔坐标系的不足
图1为笛卡尔坐标系,车辆在弯道处的行驶路径如图1右侧所示。不难发现,普通的笛卡尔坐标系不易描述曲线道路,对于弯道上行驶的车辆更难以确定道路边界与车辆的位置,更不便于规划换道轨迹。
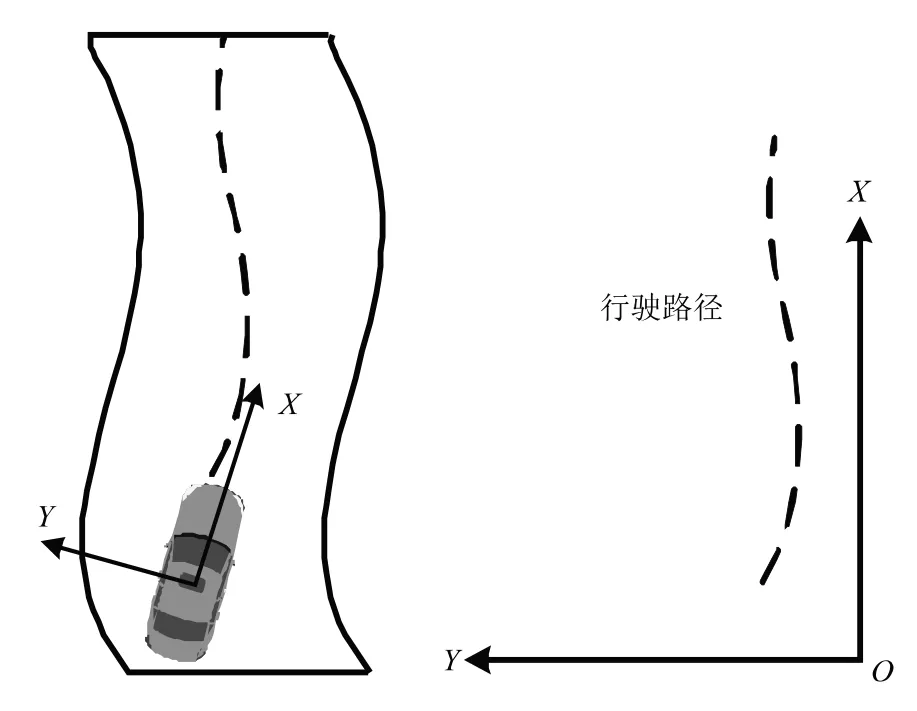
图1 笛卡尔坐标系
1.2 转换为Frenet坐标系
图2展示了车辆在Frenet坐标系下弯道处的行驶路径。它由轴和轴构成,轴沿着道路前进方向,也被称为纵向位移,向前为正值;轴垂直于道路前进方向,称为横向位移,向左为正值。李萌提到在规划问题中可以将笛卡尔坐标系转换为Frenet坐标系,可以准确定位车辆在道路上的坐标与坐标,便于将横向的规划与纵向的规划问题解耦,使得复杂的三维规划问题易于解决。
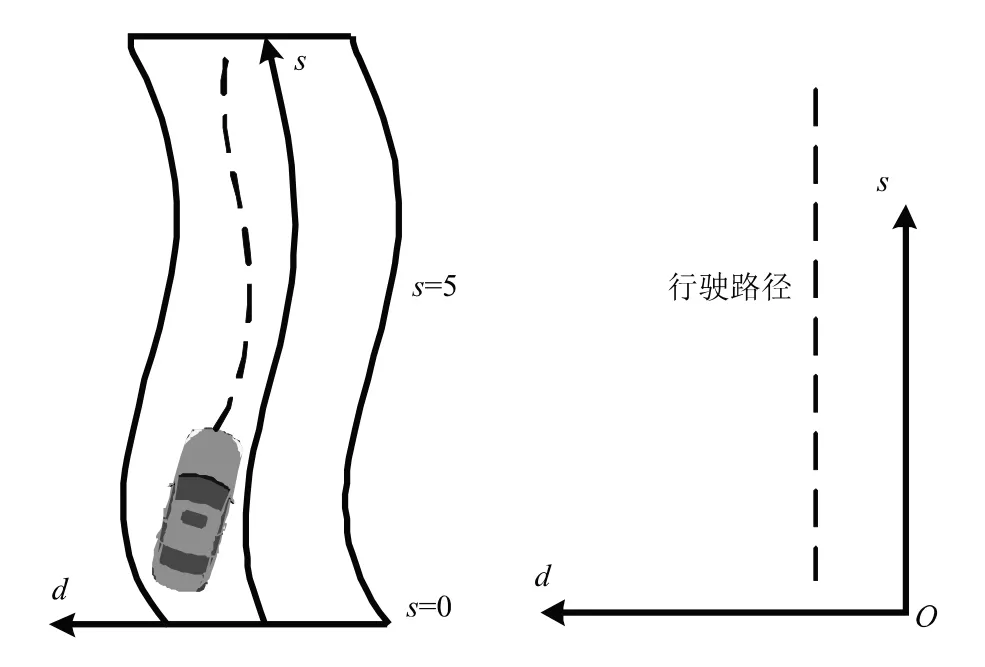
图2 Frenet坐标系
本文后续的研究均基于Frenet坐标系下进行,此坐标系相关参数如表1所示。

表1 Frenet坐标系各参数含义
2 车辆运动学模型建立
前文提到的Frenet坐标系简化了弯道换道规划的复杂度,而在后文中为实现对规划轨迹的跟踪,需要对车辆的运动过程在笛卡尔坐标系下建模。如图3所示建立运动学模型。图中是车辆的纵向速度,为前轮的转向角,为前后轴轴距,为车辆航向角。其基于以下假设:(1)不考虑汽车的垂直运动,即只有平面的运动;(2)假设左右轮胎相同,即在任意时刻都拥有相同的轮速和转角,可以合并为一个轮胎;(3)整个车身和悬架都视为刚性模型;(4)车辆的运动和转向都是由前轮驱动和转向。
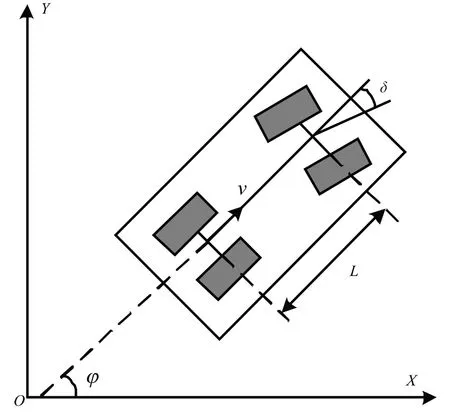
图3 车辆运动学模型
由此可建立车辆运动学方程为

3 弯道换道轨迹规划
3.1 轨迹规划背景条件
局部的轨迹规划与普通的路径规划不同,它是利用一系列带有时间序列的路径点生成最终的行驶轨迹。吴树凡等人提出对于弯道路段,传统的多项式曲线构造轨迹存在数值计算复杂,难以保证实时性,且不易考虑动态障碍物等困难。故本文采用将弯道处换道的轨迹解耦为横向的轨迹规划与纵向的速度规划。横向的规划输出轨迹曲线,决定行驶轨迹的形状,纵向规划输出平滑的速度序列,同时应考虑动态障碍物。
3.2 横向轨迹规划
3.2.1 四种横向换道轨迹曲线对比
图4对比了弯道的四种换道轨迹规划方法,对于弯道路段的轨迹主要应考虑曲线曲率的连续性。Dubins曲线的轨迹曲率出现了两次跳变,不满足行驶标准。sin正弦函数曲线和bessel曲线虽然曲率连续,但曲率在开始换道时和换道结束后不为0,这将导致车辆换道结束后方向盘不能复位,会继续偏离车道行驶,故这两种换道轨迹也不满足行驶标准。三次B样条曲线不但保证曲率连续,还解决了以上几种曲线存在的缺点。
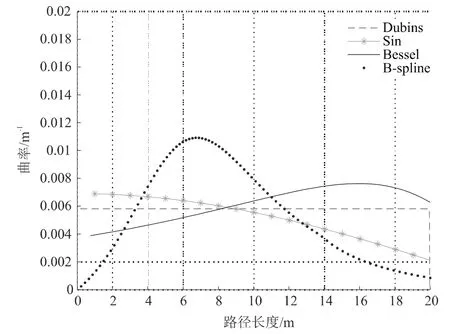
图4 换道轨迹曲率对比
3.2.2 准均匀三次B样条曲线
B样条曲线是所有B-样条基函数的线性组合。定义阶B样条函数为
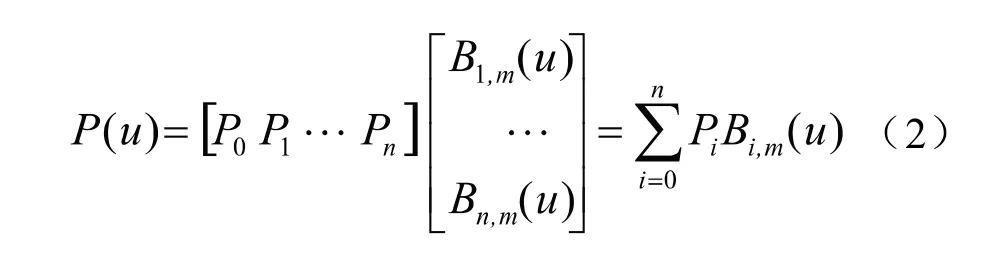
式中,B()是第个阶B样条基函数,与控制点P相对应。三次(四阶)B样条曲线可由6个控制点生成,故式中为5,为4。上文已经提到三次B样条曲线能保证曲率连续,而准均匀三次B样条函数不但所有基函数都是相同的形式,而且函数两端具有重复的性质,这降低了计算的复杂度。所以选取其进行在弯道处横向规划轨迹,结果如图5所示。
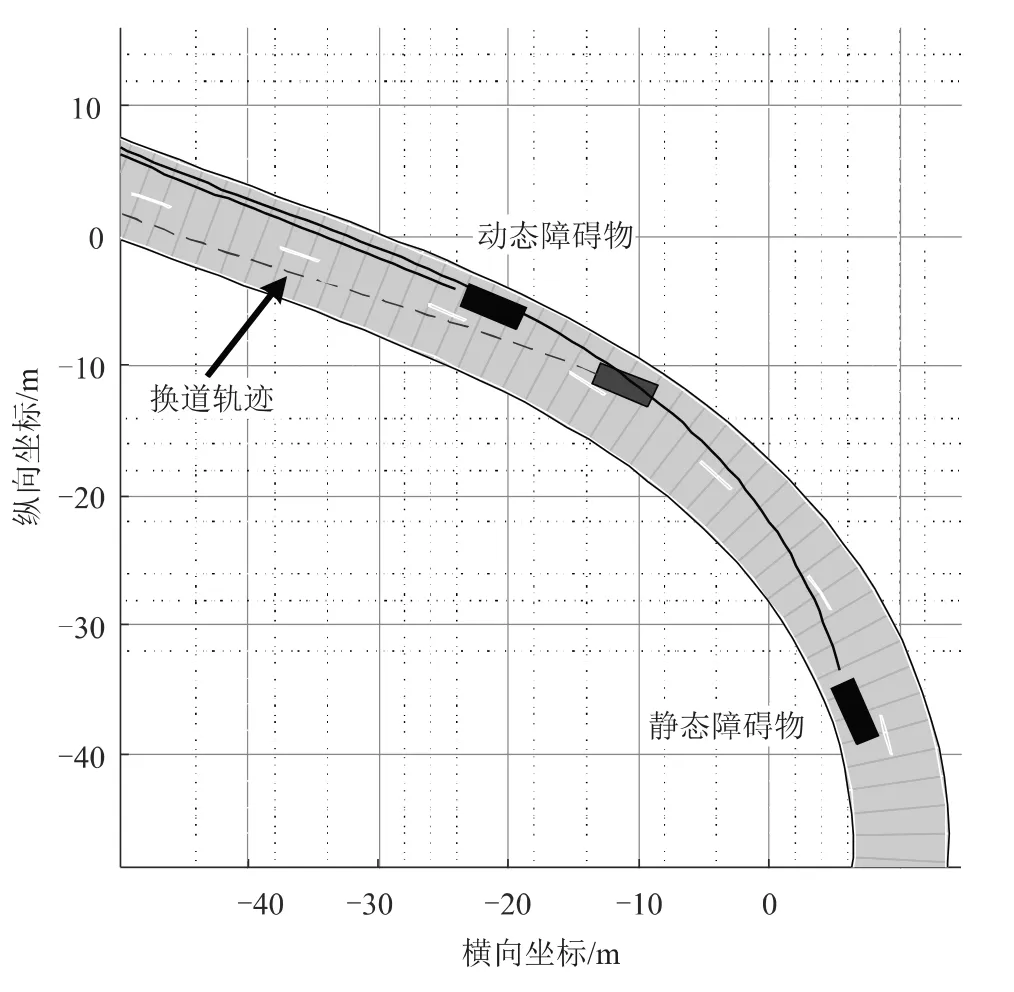
图5 准均匀三次B样条换道轨迹
3.3 纵向轨迹规划
3.3.1 动态规划初步得到速度序列
纵向规划的本质是横向规划得到的轨迹基础上加入时间序列,计算出行驶到每一个轨迹点的包含时间的速度序列。纵向规划基于图,如图6所示,即为Frenet坐标系下的纵坐标,代表时间。
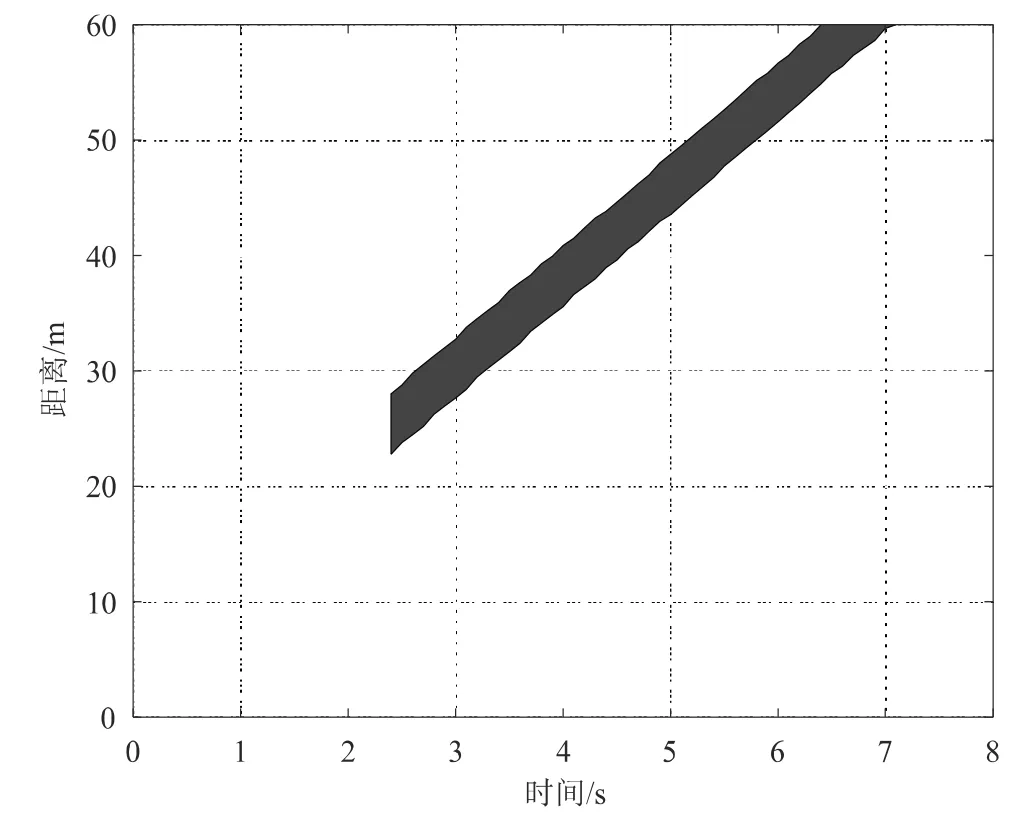
图6 s-t图
图中黑色区域代表了其他动态交通车在本车行驶轨迹上的占用,若将此区域视为搜索禁区,可以将纵向的最优速度序列求解问题转化为求解多阶段决策的动态规划问题。
3.3.2 二次规划平滑速度序列
由动态规划初步得到的速度序列,曲线不连续不可导,车辆按照此速度序列行驶会引起人极大的不适感。故利用二次规划思想对其进行优化,定义平滑后的每段曲线由五次多项式曲线拟合,构造如式(3)所示:
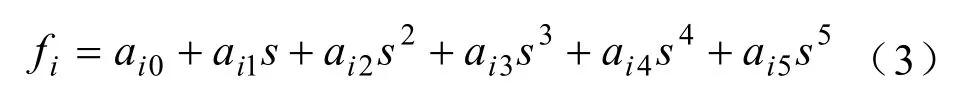
二次规划问题代价函数构造如式(4)所示:

其中,、为两个优化目标的权重比例。f代表规划轨迹的加速度,优化后应使其尽可能小。s-代表二次优化后轨迹与原动态规划轨迹的误差,优化目的是误差应尽可能小。最终二次规划平滑后速度序列曲线如图7所示,可看出规划曲线平滑并且可以躲避动态障碍物。

图7 二次规划后平滑曲线
4 轨迹跟踪控制
MPC整体分为三个部分:模型、预测和控制。本文通过车辆运动学来建立模型部分,将其转化为线型状态空间方程。预测部分是根据状态空间方程模型,顺序递推从而获得状态量。控制部分则是在每一时刻构建最优控制量,使得目标函数最优,即实现最优的跟踪控制。
图8为利用MPC对弯道处换道轨迹的跟踪图,可以看到跟踪效果良好。

图8 轨迹跟踪图
图9为轨迹跟踪过程的横向误差图,可知整个弯道换道过程的横向误差控制在±0.04 m之内。
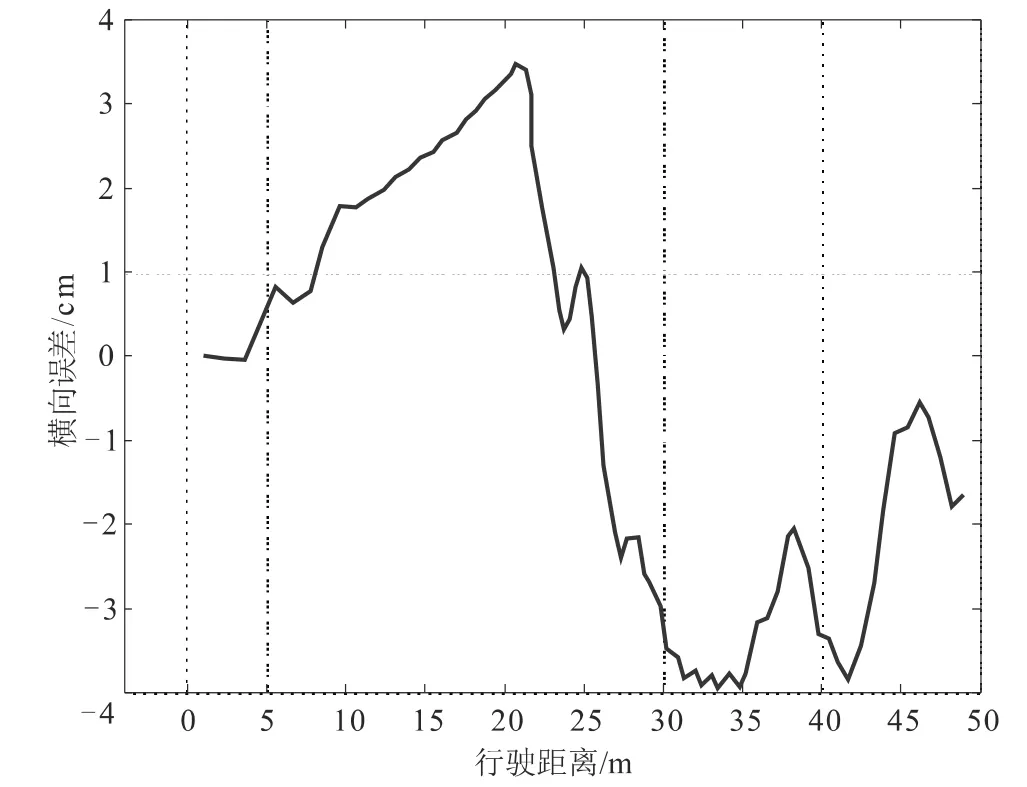
图9 横向误差图
图10为轨迹跟踪过程中的速度误差图,由图可知实际轨迹的行驶速度略高于规划轨迹的速度,误差在+0.2 m/s之内。但前文在纵向速度规划 过程中已经避让了动态障碍物,故确保了行驶的安全性。

图10 速度误差图
5 总结与不足
本研究基于Frenet坐标系,重点研究了弯道处变道的轨迹规划与跟踪控制的问题。所提出的横纵向解耦的轨迹规划方法能规划出满足曲率连续,安全避开动态障碍物的换道路径曲线。模型预测控制能精准跟踪规划路径,并有良好的鲁棒性。不足在于采用了简单的车辆运动学模型,但实际的换道过程中车速一般很高,应考虑车辆动力学模型更符合真实情况。
