基于MMC直流阻抗重塑的直流故障限流控制策略

2022-11-01吴轲郭约法梁伟锋邓文军

南方电网技术 2022年9期

吴轲，郭约法，梁伟锋，邓文军

(1. 广东电网有限责任公司东莞供电局，广东东莞 523008；2. 四川大学电气工程学院，成都 610065)

0 引言

随着风电、光伏等新能源并网外送需求的急剧增长，基于模块化多电平换流器(modular multi-level converter, MMC)的柔性直流输电技术被广泛应用到新建直流工程中，为未来直流电网的构建打造雏形[1 - 4]。考虑到传输距离和维护成本，架空线将逐渐取代电缆成为柔性直流输电系统中的主要输电线路形式[5 - 7]。裸露在户外的架空线发生短路故障的概率较电缆高得多。相比于交流电网，主要由电力电子设备构成的柔性直流输电系统是一个低惯量、弱阻尼系统，因而故障电流将在极短时间内达到电力电子设备耐受电流的几十倍[8 - 9]。

直流断路器是目前隔离直流故障的主要设备，但其主要指标(开断电流和开断容量等)受到技术限制无法完全满足故障清除的可靠性要求[10]。因此，直流故障限流装置应运而生。其中最普遍的做法是在换流站出口处加装限流电抗器。虽然这种方法原理简单、效果显著，但直流侧的大电感会降低系统控制的响应速度，从而引起功率振荡甚至引发失稳现象[11]，保证直流输电系统的稳定运行必然要牺牲限流电抗器的限流作用[12]。利用超导材料或大功率半导体构成的故障限流器虽然能兼顾直流系统的稳态运行特性和限流效果[13 - 16]，但仍有许多技术问题尚未解决，在实际工程中使用的可靠性难以保证。

文献[17]分析了MMC交、直流侧故障后的过电流特性，提出将限流元件的特性映射到控制系统的虚拟阻抗控制策略。文献[18]提出了一种在内环直流电流控制器附加直流电流指令动态限幅控制的限流策略，基于预设的目标控制曲线将直流电流控制在限流要求范围内，然而该策略仅适用于混合型MMC系统中。文献[19]通过分析得出了在故障后降低每相子模块投入的数量可有效限制MMC型直流变压器的故障电流，并设计了一种通过调整桥臂电压直流分量和交流分量来减少子模块投入数量的主动限流控制方法。文献[20]将前述方法应用到MMC换流器中，并对限流控制策略进行了改进。然而，这两篇文献均未定量分析子模块投入数量对故障电流的影响规律，导致限流策略的理论基础薄弱，控制参数依靠经验获得。

针对前述问题，本文建立了计及子模块投入比例的MMC直流阻抗模型，揭示了换流器电路参数和控制参数对直流阻抗以及故障电流的影响规律，并提出基于直流阻抗重塑的故障限流控制策略。

1 适用于故障分析的MMC直流阻抗模型

1.1 MMC的拓扑结构与控制策略

三相MMC的基本结构如图1所示。MMC的6个桥臂均由N个完全相同的子模块(sub-module，SM)和桥臂电感Lm、桥臂电阻Rm串联组成。目前工程中子模块大多采用半桥结构，每个半桥型子模块中两个IGBT和两个反并联二极管构成一个半桥，Cm为子模块电容，uC为电容电压，每个子模块通过各自的连接端口串联接入到主电路中，直流母线的电压udc由每个子模块中的电容电压串联叠加而成。交流系统部分，ue为等效电源电压幅值；Re和Le分别为等效电源的等效电阻和电感；Rt和Lt分别为换流变压器的等效电阻和电感，Kt为换流变压器的变比；us和is分别为公共耦合点(point of common coupling，PCC)的电压和电流；Ps和Qs分别为PCC点流入换流站的有功功率和无功功率。

图1 MMC结构示意图Fig.1 Structure diagram of MMC

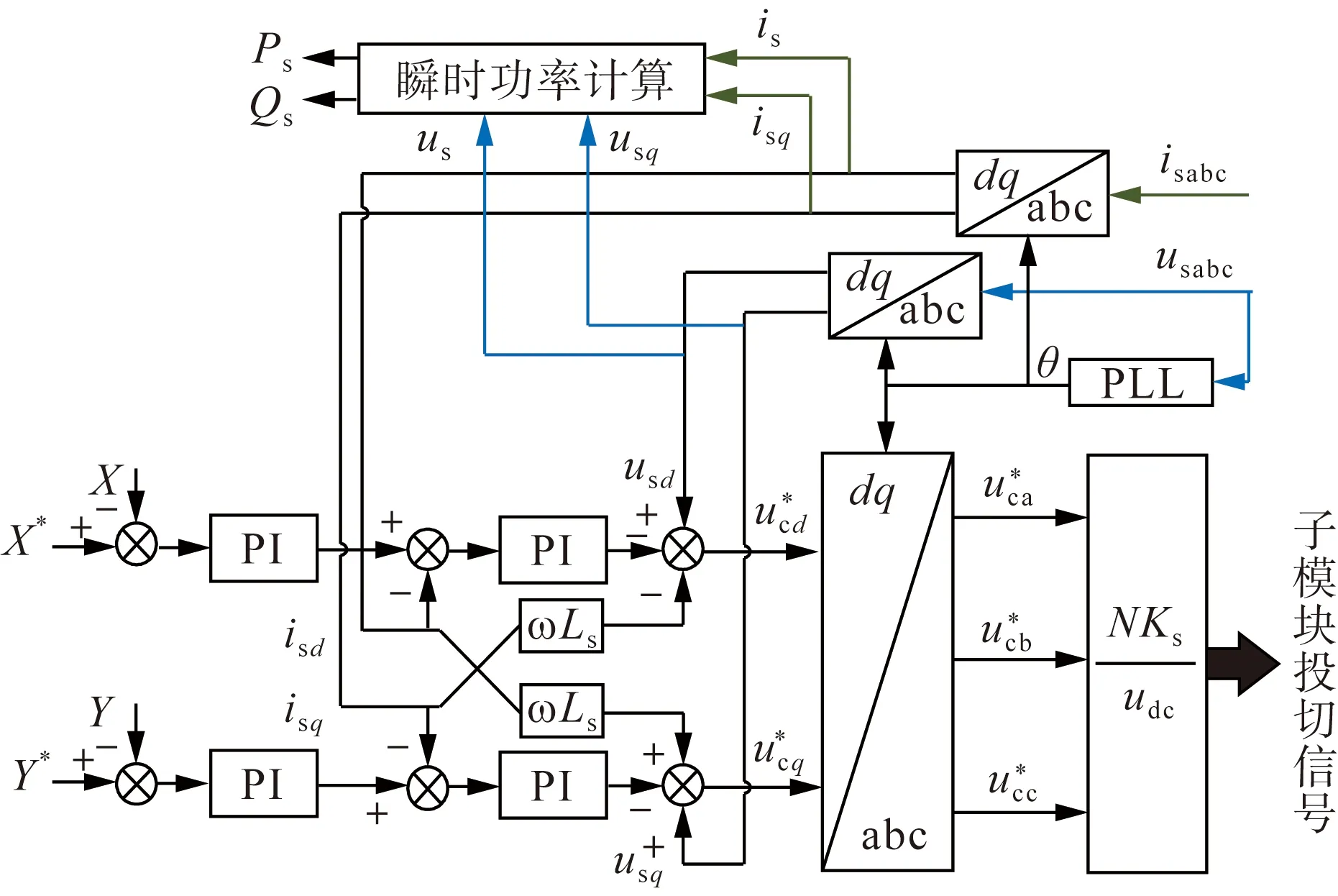
图2 MMC控制策略框图Fig.2 Block diagram of MMC control strategy

1.2 MMC等效电路

从交流侧看，MMC可以等效为受控电压源形式[21]，从直流侧看，根据功率平衡原理可以将MMC等效为受控电流源形式[22]，则将MMC简化得到如图3所示的等效电路，MMC等效参数可通过式(1)计算得到。

图3 MMC等效电路Fig.3 Equivalent circuit of MMC

(1)

式中：Req、Leq、Ceq分别为MMC的等效电阻、等效电感和等效电容；Rm、Lm、Cm分别为MMC的电阻、电感和电容；N为任意时刻每相投入的子模块数。

根据图3，MMC注入的直流侧有功功率Pdc可以表示为：

Pdc=id·uceq

(2)

式中：uceq为直流电容电压；id为阀侧向换流器注入的电流。

对式(2)进行线性化得：

Δpdc=uceq0·Δid+id0·Δuceq

(3)

式中：下标“0”表示该变量的稳态值；Δpdc为直流功率扰动量；Δid为阀侧向换流器注入电流扰动量；Δuceq为电容电压扰动量。

进一步结合等效电路结构和电路相关定律推导得出Δpdc、Δidc和Δudc之间的关系如式(4)所示。

(4)

式中：Ldc为MMC的直流阻抗，Ldc=Leq+2Ld=Δudc/Δidc；Ld为直流平波电抗；s为复频率；Δidc为直流电流扰动量；Δudc为直流电压扰动量。

下一节将针对不同控制模式推导直流阻抗的表达式。

1.3 MMC直流阻抗模型

1.3.1 定有功功率控制换流器直流阻抗模型

对于采用定有功功率控制的换流器，当忽略换流器的功率损耗时，可以认为注入换流站的交流功率与功率控制器的参考值是一致的。即使直流线路发生故障，故障后注入的功率也能在短时间(几毫秒)内保持不变[23]。因此，直流功率偏差量Δpdc在故障的初始阶段内为0，即：

Δpdc=uceq0·Δid+id0·Δuceq=0

(5)

整理式(5)可得到Δid与Δuceq的关系式，并代入式(4)推导得到直流阻抗为：

(6)

1.3.2 定直流电压控制换流器直流阻抗模型

在直流输电系统中，采用定直流电压控制的换流站负责平衡直流系统的有功功率，因此，注入到换流器中的功率将随直流电压的波动而变化。故障后直流电压因子模块电容放电而急剧下降，此时Δpdc不再等于0。采用定直流电压控制换流器的注入功率pdc可由式(7)表示。

(7)

式中：usd0为交流电压d轴分量的稳态值；isd为d轴交流电流；Rs和Ls为等效交流侧电阻和电感，可通过式(8)计算得到。

(8)

为简化分析，内环控制可等效为时间常数为τ的延时环节，定直流电压控制下的isd表达式(9)可以简化为：

(9)

将式(9)代入式(7)，并线性化得：

(10)

联立式(3)—(4)和式(10)，可得定直流电压控制换流器的直流阻抗为：

(11)

1.4 考虑子模块投入比例的直流阻抗模型

为将子模块投入运行的比例考虑到直流阻抗建模中，引入系数Ks表示桥臂中参与投切子模块的比例，如图2所示。正常运行时Ks=1，表示桥臂中所有子模块参与运行；当所有子模块均被旁路时，Ks=0；当Ks∈(0,1)，则表示比例为(1-Ks)的子模块被旁路。引入系数Ks后，Δuceq和Δid将改写为：

(12)

当部分子模块被旁路后，MMC的等效电容也将发生变化。根据能量守恒定理可得：

(13)

整理式(13)得到部分子模块旁路后的等效电容为：

(14)

式(3)和式(4)也分别改写为：

Δpdc=u′ceq0·Δi′d+Δi′d0·u′ceq

(15)

(16)

将式(15)和式(16)分别代入式(5)和式(6)，推导得到不同控制模式下考虑子模块投入比例的直流阻抗表达式分别如式(17)—(18)所示。

(17)

(18)

根据文献[24]，直流故障电流可由稳态运行电流分量idc0和故障分量if相加得到。以定有功功率换流站出口故障为例，故障分量if的频域表达式为：

(19)

若要将子模块旁路的限流效果计入到直流阻抗的修正中，则可使直流电压保持不变，将式(18)中的系数Ks计入直流阻抗中，得到修正后的直流阻抗如式(20)和式(21)所示。

(20)

(21)

2 影响直流故障电流的关键因素分析

由式(21)可以看出，故障电流的故障分量大小由故障点的电压和直流阻抗决定，而稳态分量则由稳态潮流分布决定。因此，影响故障电流的因素分为两部分，即稳态运行参数和直流阻抗特性。稳态运行参数包括稳态运行电流和直流电压两方面，分别影响稳态分量和故障分量。直流阻抗特性主要影响故障分量，由式(19)—(20)可归纳出影响直流阻抗特性参数为稳态参数uceq0、id0、usd0、isd0，交流电路参数Rs、Ls、换流器电路参数Req、Ceq、Ldc，控制参数kp、ki、Ks。

随着故障的发展，稳态分量在故障电流中的占比急剧减小，因此，在辨析关键因素时重点关注其对故障分量的影响。在换流站输入功率确定的情况下，稳态参数对直流阻抗的影响可忽略不计。换流站参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

交流电路参数由交流系统阻抗参数和换流变压器阻抗参数决定，可控性不强，因此，接下来仅对换流器电路参数和控制参数进行重点分析。

2.1 换流器电路参数的影响

以定直流电压换流站出口发生极间短路故障为例，设置初始潮流为零，分别绘制出桥臂电阻、桥臂电感和子模块电容取不同数值时的直流阻抗频域幅值图和故障电流曲线，分别如图4—6所示。

图4 桥臂电阻对直流阻抗及故障电流的影响Fig.4 Effect of arm resistance on DC impedance and fault current

由文献[25]的理论推导可知，信号的高频部分决定了该信号在时域中的初始阶段特性，因此，初始阶段故障电流主要受直流阻抗高频部分特性的影响。

由图4可以看出，桥臂电阻主要影响直流阻抗的中频段，桥臂电阻值越大，中频段的阻抗幅值越大，相应地，故障电流越小。然而，桥臂电阻的阻值很小，通常可忽略不计，并且对高频段几乎无影响，因而其对故障电流的影响微乎其微。

由图5可以看出，在中高频段，桥臂电感越大，直流阻抗的幅值越大，且在高频段呈现均匀增长的趋势，故障电流也随之显著减小。

图5 桥臂电感对直流阻抗及故障电流的影响Fig.5 Effect of arm inductance on DC impedance and fault current

由图6可以看出，子模块电容对直流阻抗的中频段有较大的影响，从能量的角度来看，子模块电容越大的换流器在故障后释放的能量越大，故障电流也越大。

图6 子模块电容对直流阻抗及故障电流的影响Fig.6 Effect of sub module capacitance on DC impedance and fault current

2.2 控制参数的影响

同样以定直流电压换流站出口发生极间短路故障为例，设置初始潮流为0，分别绘制出外环PI的比例系数kp、积分系数ki、子模块投入比例系数Ks取不同数值时的直流阻抗频域幅值图以及故障电流曲线，分别如图7—9所示。

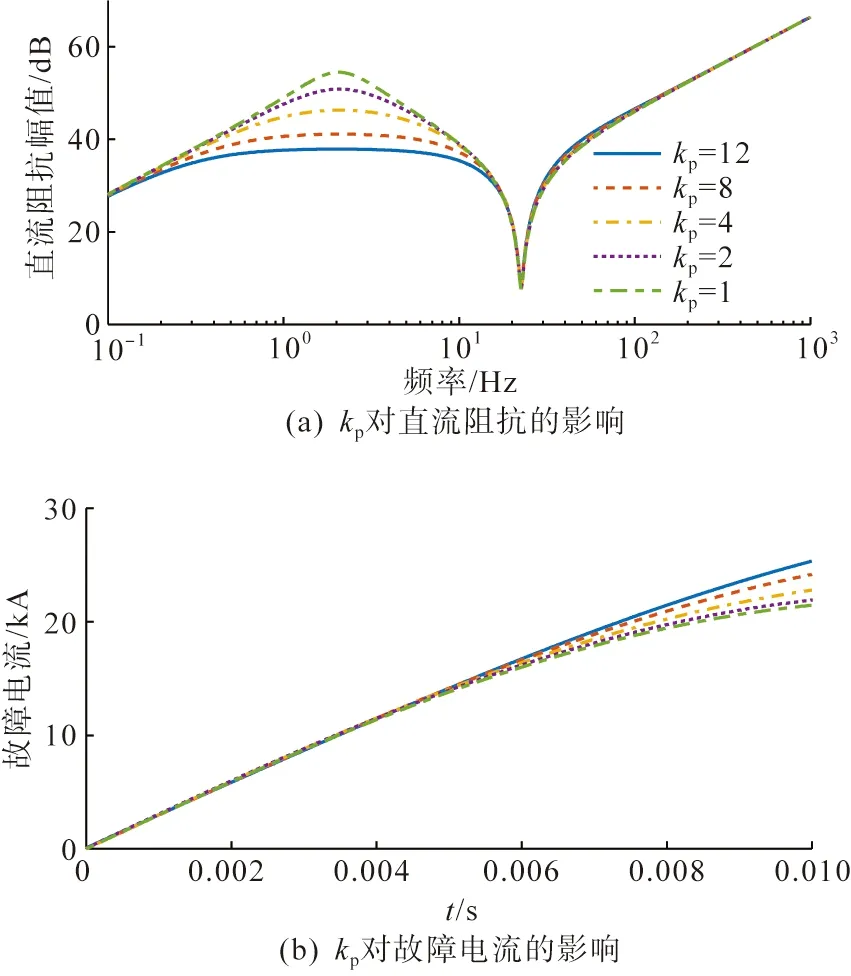
图7 比例系数kp对直流阻抗及故障电流的影响Fig.7 Effect of proportional coefficient kp on DC impedance and fault current

由图7可以看出，定直流电压控制外环比例系数kp的影响主要体现在中低频段，kp越大，中低频段的阻抗越小，且该频段阻抗的幅值变化较大。随着故障的发展，kp对故障电流的影响逐步体现，kp越大，故障电流越大。

由图8可以看出，定直流电压控制外环积分系数ki对直流阻抗的低频段影响较大，因而对初始阶段故障电流的影响可忽略不计。

图8 积分系数ki对直流阻抗及故障电流的影响Fig.8 Effect of integral coefficient ki on DC impedance and fault current

由图9可以看出，减小子模块投入运行的比例Ks可大幅增大直流阻抗的高频段幅值，前10 ms内的故障电流均呈比例下降。对比图4(a)中不同数值桥臂电感下直流阻抗的阻抗曲线可以发现，减小Ks与增大故障回路中的电感呈现相似的限流效果，均能减小故障电流的上升率。

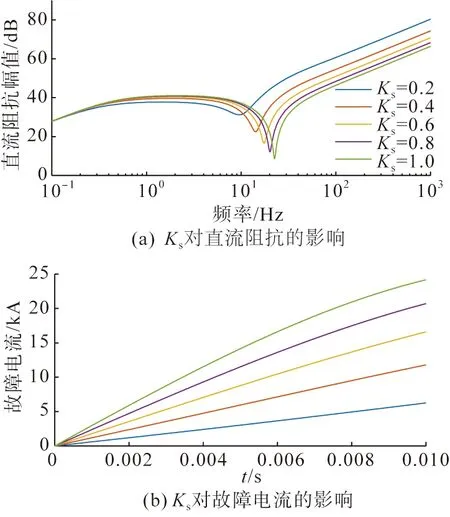
图9 子模块投入比例Ks对直流阻抗及故障电流的影响Fig.9 Effect of switching ratio Ks on DC impedance and fault current

2.3 关键影响因素总结

由2.1节和2.2节的分析可以得出结论，积分系数ki、比例系数kp、桥臂电阻和子模块电容对直流阻抗的影响体现在中低频段，因而对初始阶段故障电流的影响不明显。桥臂电感和子模块投入运行比例Ks对高频段有显著影响，通过增大桥臂电感或减小Ks均能有效降低故障电流的上升率，因此可以认为桥臂电感和子模块投入运行比例Ks为影响直流故障电流的关键因素。

3 基于直流阻抗重塑的故障限流控制策略

增大电感值的限流方法易造成直流系统响应速度降低、动态性能恶化等问题，引发直流系统失稳现象。而在故障后通过旁路部分子模块的方法抑制故障电流上升的方法不仅可以有效达到限流效果，而且对稳态运行无影响。因此，可设计一种故障后自适应减小Ks的控制策略来达到限流目的。

3.1 直流阻抗重塑方法

由2.2节中的故障电流曲线可以看出，在故障后的初始阶段(尤其是前6 ms内)，PI参数对故障电流几乎无影响。为简化限流控制的设计，进一步将直流阻抗简化为等效电感、等效桥臂电阻和等效子模块电容串联而成的RLC等效阻抗Zdc。

(22)

若要减小故障电流上升率、上升值等指标，只需增大直流阻抗高频段的幅值。因此，引入一阶因子1+Tss与未考虑Ks的直流阻抗相乘，得到重塑后的直流阻抗Zlim为：

(23)

如图10所示，增大一阶因子的时间常数Ts可有效增大直流阻抗高频段的幅值，并且保留中低频段的特性。

图10 Ts对直流阻抗的影响Fig.10 Effect of Ts on DC impedance

3.2 故障限流控制策略

基于以上限流原理设计了一种直流故障限流控制策略如图11所示。

图11 直流故障限流控制策略框图Fig.11 The diagram of the DC fault current limiting control

限流控制分为启动控制和Ks信号发生控制两(22)—(23)得到直流阻抗的表达式如式(24)—(27)所示。

(24)

(25)

(26)

(27)

分别将式(24)—(27)代入式(21)中的Z″Udc即可得到故障电流的计算值。Ks分别取1和0.8时，定有功功率站和定直流电压站出口发生极间短路故障时故障电流计算值和仿真值的对比曲线如图11所示。

由图12可以看出，基于直流阻抗的故障电流计算方法具有较高的准确性，不同控制模式、不同子模块投入比例下计算曲线和仿真曲线的吻合度较高，定有功功率站中两者的最大相对误差分别为1.9%和0.5%，定直流电压站中两者的最大相对误差分别为2.1%和1.5%，均满足计算精度要求，由此验证了所建立直流阻抗模型的准确性。

图12 Ks取不同值时故障电流计算值和仿真值的对比Fig.12 Comparison between calculated value and simulation value of fault current when Ks takes different values

3.3 故障限流控制策略的限流效果验证

为验证故障限流控制在Ts取不同值时表现出的限流效果，分别在Ts取0.002 s、0.004 s和0.006 s这3种情况下对直流故障进行仿真，控制参数如表2所示，仿真结果如图12所示。

表2 Ts取不同值时的控制参数值Tab.2 Control parameters values when Ts takes different values

由图13(a)可以看出，Ts越大，故障电流的上升率越小，同时刻的故障电流值越小，这与图9的分析结论一致。与未投入限流控制情况的故障电流相比，3种参数下6 ms时刻的故障电流分别下降了30.42%、40.23%、44.18%，限流效果显著。

图13 Ts取不同值时的故障限流效果对比Fig.13 Comparison of fault current limiting effects when Ts takes different values

所提限流控制策略能够根据直流电压值和直流电流值实时调整Ks的值，使得直流电压维持在一定水平，有利于故障处理后系统重新建立直流电压、恢复功率传输。

3.4 故障限流控制策略的限流性能分析

设置无限流措施(方案1)、所提限流控制(方案2)、增加限流电感(方案3)、子模块全闭锁(方案4)4种方案，通过分析对比不同方案下的故障特性来验证所提限流控制策略的限流效果。设定t=1s时定直流电压站出口发生极间短路故障，限流控制Ts取0.002，限流电感增加100 mH，故障期间闭锁子模块过流保护，直流断路器在故障后6 ms开断，实现故障电流的清除。4种方案的仿真对比结果如图14—17所示。

图14 不同方案的限流效果对比Fig.14 Comparison of fault current limiting effects with different schemes

与无限流措施相比，3种限流方案均能有效降低故障电流。就限流效果而言，方案3和方案4中直流断路器的最大开断电流分别降低了35.3%和44.5%，采用所提限流控制则降低了48.2%，有利于降低直流断路器的设计和开断要求。

就故障清除时间而言，增加限流电感的方法同时也增大了回路中的阻抗，使得故障清除时间增加，与无限流措施相比，故障清除时间延长了10.3%；方案2和方案4闭锁部分或全部子模块，抑制了子模块电容的放电，使得直流断路器开断时耗散的能量减少，因而故障清除时间分别减少了21.5%和28.8%。

图15给出了4种方案中直流电压的仿真波形。方案2中直流电压随着限流控制的启动动态下降，最低降至额定电压的26%，当直流断路器启动后，限流控制退出运行，换流器恢复子模块的正常投切，在直流电压控制的作用下，直流电压逐渐恢复至额定值附近。方案4在故障后将所有子模块闭锁，直流电压降至0，直流断路器启动后解锁子模块，重新对子模块电容充电，直流电压逐渐恢复，并出现过电压现象。方案2增大电感会恶化系统的动态性能，减缓了直流电压的恢复速度。所提控制策略有利于故障后系统的快速恢复。