计及遮雨帽和隔音装置的空心电抗器散热性能分析及结构参数优化设计

陈炜，胡胜，卢铃，唐奇，曹浩

(1. 国网湖南省电力有限公司电力科学研究院，长沙 410007；2. 国网电力设施噪声与振动实验室，长沙 410007)

0 引言

干式空心电抗器因具备结构简单、线性度高和重量轻等优点，在电力系统中得到了广泛应用[1 - 2]。然而，空心电抗器在实际运行过程中易发生过热、烧伤甚至起火烧毁等故障，研究表明包封线圈局部温度过高是主要原因[3]。目前，为降低环境因素(特别是雨水)对电抗器的影响，常在电抗器端部加装遮雨帽[4 - 5]；为降低电抗器周围噪音，常在电抗器周围安装隔音装置。然而，电抗器线圈产生的热量使周围流体向上流动，遮雨帽和隔音装置阻碍了流体的流动，导致电抗器包封线圈的散热能力降低，温升显著增加。因此，为了提高电抗器的散热能力，在准确计算空心电抗器温升的基础上开展遮雨帽和隔音装置结构参数的优化研究至关重要。

在电抗器温升计算方面，文献[6 - 7]介绍了变压器绕组的平均温升计算方法，该方法精度较低。文献[8]将电抗器包封线圈的散热过程等效为竖直管道，给出了温升解析计算方法，该方法仅适用于气道两侧包封壁面的热流密度。文献[9]由传热学准则式推导出电抗器包封壁面沿轴向的对流传热系数表达式，进而计算出电抗器的绕组温升分布，然而该方法无法获得电抗器详细的温度场和流场分布。在此基础上，文献[10]推导出在加遮雨帽工况下的温升解析式，但该方法受制于包封线圈壁面对流传热系数，计算精度较低。相比于平均温升和解析计算方法，采用有限元法能够获得详细的温度场和流场分布，被广泛应用于电抗器/变压器等电工装备的温度场计算中[11 - 12]。文献[12 - 15]建立了空心电抗器温度场仿真模型，采用包封线圈温度与周围流体耦合的方法获得了电抗器详细的温度分布。然而，上述方法未考虑遮雨帽和隔音装置对电抗器温度场分布和散热特性的影响。

在电抗器热优化方面：文献[17 - 18]提出了通过调整包封线圈高度和气道宽度等方法以提高线圈-气道单元散热能力，该方法适用于未加遮雨帽和隔音装置的工况。在此基础上，相关文献开展了关于空心电抗器遮雨帽和隔音装置的优化研究，考虑到遮雨帽对电抗器温升的影响，文献[19]将遮雨帽等效为倾斜挡板，通过调整包封线圈参数以提高线圈散热能力。文献[3]采用有限元法分析了在强制风冷条件下遮雨帽结构对气道内流体流速的影响规律，通过调整遮雨帽结构参数能够实现包封线圈间气道内流体流速基本相同。考虑到隔音装置对电抗器温升的影响，文献[14]建立了考虑隔音装置下空心电抗器温度场仿真模型，分析了隔音装置结构参数对电抗器温升的影响规律，获得了最佳的设计参数，能够在一定程度上降低电抗器的温升。然而，遮雨帽和隔音装置结构参数对电抗器散热能力的影响复杂，上述方法仅从局部开展遮雨帽或隔音装置的优化设计，无法实现电抗器整体散热性能的优化，限制了其实际应用。

本文建立空心电抗器流场-温度场三维仿真模型，分析了加遮雨帽和隔音装置前后电抗器温度场和流场分布特点，给出了加遮雨帽和隔音装置工况下电抗器温升显著增加的原因。在此基础上，采用拉丁方试验设计和有限元仿真计算相结合的方法，构建了电抗器包封线圈最高温度与遮雨帽、隔音装置结构参数间的Kriging模型，获得了各参数对电抗器最高温度的影响规律。采用粒子群优化算法获得最佳的遮雨帽和隔音装置结构参数，结果表明优化方法能够显著降低空心电抗器的温升。

1 空心电抗器基本结构及等效模型

1.1 基本结构及参数

本文以额定电压为220 kV，电流为1 800 A，电感为21 mH的干式空心电抗器作为研究对象。空心电抗器的本体结构是由多个同轴的包封线圈组成，各包封线圈在电气上并联连接，相邻包封间采用气道隔开，气道内由引拔条撑起，起到绝缘和散热的作用。线圈由多根并联圆导线或扁导线组成，每根导线上包有聚酯薄膜作为匝绝缘，包封由内向外依次为导体、绝缘材料和环氧玻璃纤维，包封上下端由星形架连接，起到加固和分配电流的作用。基于上述的技术参数和结构型式，设计的电抗器主要参数如下：线圈高度为1.5 m，气道宽度为0.025 m，线圈内外半径分别为0.3 m和1.0 m，包封数量为12。电抗器线圈顶端和底端安装星形架，其长度、宽度和厚度分别为2.0 m、0.1 m和0.1 m，沿圆周呈45 °排列，结构如图1所示。

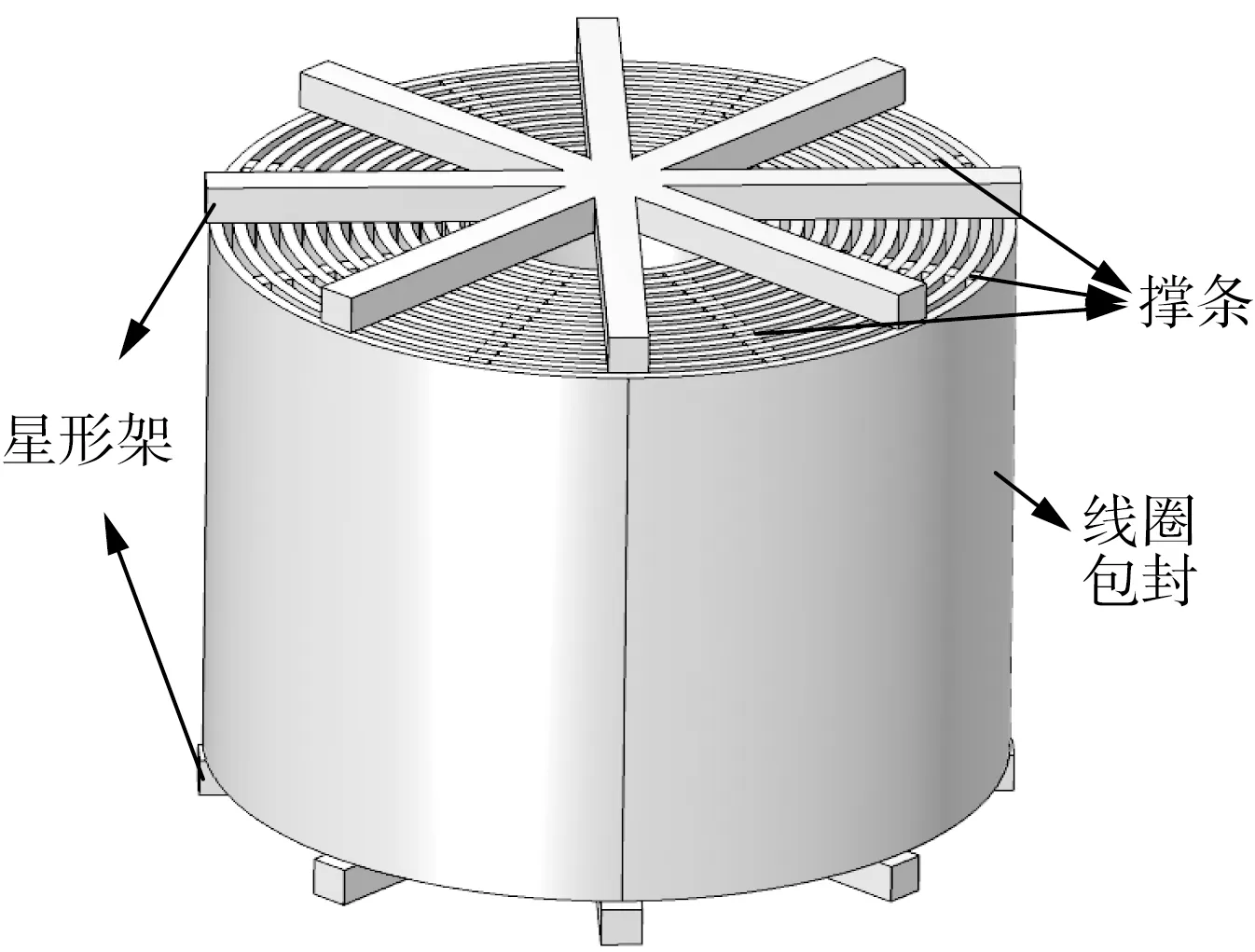
图1 空心电抗器基本结构Fig.1 Basic structure of air core reactor

1.2 等效模型

根据空心电抗器结构参数，利用COMSOL仿真软件建立了三维模型，考虑到计算的准确性及计算时长，仿真模型做了如下简化和等效：1) 模型中仅考虑包封线圈稳态散热过程，忽略包封间撑条和绝缘支柱对电抗器温升的影响；2) 为了兼顾计算精度和时长，整个计算域为正方体，边长为6 m，空心电抗器三维等效模型如图2所示。

图2 空心电抗器三维等效模型 Fig.2 Three dimensional equivalent model of air core reactor

2 电抗器流场-温度场仿真计算

2.1 流场-温度场仿真计算

热源计算、控制方程、边界条件设置和网格剖分是准确获得电抗器温度场的关键步骤。

1)热源计算

空心电抗器的损耗主要由包封线圈损耗和星形架损耗构成，线圈损耗由电阻损耗和涡流损耗组成。根据电抗器包封线圈电流和周围磁场分布，可以得到电抗器各包封线圈的总损耗。基于星形架的结构尺寸和周围磁场分布可以得到星形架的损耗。将上述计算得到的损耗施加在仿真模型中，作为电抗器温度场仿真模型的热源。

2)控制方程

空心电抗器热源主要来自包封线圈和星形架的损耗，线圈和星形架产生的热量主要通过热传导、热对流和热辐射的方式向外传递。在电抗器线圈和星形架固体区域，热量主要以热传导的方式从高温区域向低温区域传递；考虑到电抗器内部相邻包封线圈的温升差别不大，在电抗器内部包封线圈表面，热量主要以热对流的方式与周围流体进行换热；在最内包封线圈内表面、最外包封线圈外表面和星形架表面，主要通过热对流和热辐射进行散热。其控制方程可参考文献[20 - 21]。

3)边界条件设置

根据图2的空心电抗器三维模型，温度场仿真的边界条件按如下方式进行设置：温度场采用层流和流体传热2个模块，电抗器包封线圈和星形架为设置为静止壁面，各方向速度均为0；整个模型下底面设置为入口，前后侧面、左右侧面和上表面设置为出口，法向速度为0，表面温度设置为环境温度；考虑到最内最外包封线圈和星形架表面的热辐射过程，设置其表面发射率为0.9。其中环境温度设置为20 ℃。

4)网格剖分

网格的疏密程度直接影响到温度场仿真计算的准确性，为了兼顾计算精度和计算速度，采用自由剖分网格，在靠近包封线圈和星形架位置处网格剖分密集，在远离包封线圈位置网格剖分稀疏。网格剖分结果如图3所示。

图3 网格剖分结果 Fig.3 Results of mesh generation

2.2 温度场仿真结果

根据上述的计算方法，仿真总时长设置为10 h，步长设置为0.1 h，容差设置为0.05。按照上述方法，计算得到的电抗器温度场仿真结果如图4所示。

由图4可知，电抗器最高温度为73.6 ℃，环境温度为20 ℃，最高温升为53.6 ℃。根据上述的仿真结果，提取了第5、6和7包封线圈的温度分布结果，如图5所示。

图5 部分包封线圈温度分布Fig.5 Temperature distributions of partially encapsulated coils

由图5可知，电抗器包封线圈温升分布规律基本相同，沿轴向方向随高度增加呈逐渐上升的趋势，最高温度位于包封线圈顶端位置。其中，电抗器各包封线圈的最高温度结果如表1所示。由表可知，电抗器内部各包封线圈最高温度基本相同。

表1 各包封线圈温度仿真结果Tab.1 Simulation results of temperature of each encapsulated coil

3 加装遮雨帽和隔音装置的电抗器温度场仿真结果与散热特性分析

3.1 温度场仿真结果

考虑到遮雨帽和隔音装置会阻碍气道内的流体流动，包封线圈散热条件恶劣，因此需分析加遮雨帽和隔音装置下电抗器温升分布特点，获得其散热特性。其中：电抗器顶端安装遮雨帽，通过绝缘支柱支撑；电抗器最外包封线圈周围安装隔音装置，呈圆筒结构，上部和下部中心开孔。遮雨帽结构参数：半径为1.2 m，高为0.3 m，遮雨帽底端与隔音罩顶端的距离为0.2 m；隔音装置参数：整体高度为1.8 m，上下中心孔半径分别为0.5 m和0.5 m，厚度为0.1 m，材料为热塑性聚酯薄膜。根据上述参数，建立了涵盖遮雨帽和隔音装置的电抗器三维模型，如图6所示。

图6 加遮雨帽和隔音装置的电抗器等效模型Fig.6 Equivalent model of reactor with rain cover and sound arrester

基于电抗器流场-温度场仿真计算方法给出了加遮雨帽和隔音装置下电抗器温度场仿真结果，如图7所示。

图7 加遮雨帽和隔音装置下温度场仿真结果Fig.7 Simulation result of temperature fields with rain cover and sound arrester

由图7可知，加遮雨帽和隔音装置后电抗器的最高温度为93.6 ℃，最高温升为73.6 ℃。对比图4的仿真结果可知，加遮雨帽和隔音装置后电抗器温升增加20.0 ℃，温升显著增加。

3.2 包封线圈散热特性分析

为了分析遮雨帽和隔音装置对电抗器包封线圈散热特性的影响规律，提取了沿不同路径下的温度场和流场分布，其中提取的路径如图8所示。

图8 路径的选取Fig.8 Selection of the paths

1)顶端位置温度分布

根据加/未加遮雨帽和隔音装置两种工况下电抗器的温度场仿真结果，绘制得到在顶端位置处各包封温度分布曲线，如图9所示。

图9 加遮雨帽和隔音装置前后电抗器温度分布Fig.9 Results of temperature fields with and without the rain cover and sound arrester

由图9可知，未加遮雨帽和隔音装置时，电抗器内部各包封线圈最高温升基本相同，最内最外包封线圈温度明显低于内部包封线圈，主要由于最内最外包封线圈一侧向气道对流换热，另一侧与周围大空间进行对流换热和热辐射，相比于内部线圈具有更好的散热条件。加装遮雨帽和隔音装置后，电抗器各包封线圈温升均有所增加，增加幅度为8～23 ℃，热点温升位于第10个包封线圈。

2)包封中轴线温度分布

为了分析电抗器包封线圈内部温度分布，提取包封线圈5、6和7中轴线位置处的温度，如图10所示。

由图10可知，加和未加遮雨帽和隔音装置时各包封线圈的温升分布趋势基本相同，随着高度的增加呈现逐步增加的趋势，在包封线圈顶端位置处略微下降，主要由于在线圈端部位置对流散热充分。加装遮雨帽和隔音装置后，包封线圈温升显著增加，位于线圈中上部位置。

图10 包封线圈中轴线温度分布Fig.10 Temperature distributions along the central axis of the encapsulation coil

3)气道中轴线温度分布

为了分析电抗器包封线圈气道内流体的温度分布，提取了包封线圈5-6和6-7间的气道内中轴线流体温度分布，如图11所示。

图11 气道中轴线温度分布Fig.11 Temperature distributions on central axis of airway

由图11可知，加和未加遮雨帽和隔音装置时，气道中轴线位置处温度分布趋势基本相同，沿轴向方向随高度增加逐渐增加的趋势；且沿着轴向方向的高度增加至1.2 m以后，温度呈急剧上升的趋势。

为分析加遮雨帽和隔音装置后对电抗器包封线圈间流体流速的影响，提取了包封线圈5-6和6-7间气道中轴线位置处轴向流速分布，如图12所示。

图12 气道中轴线轴向流速分布Fig.12 Distributions of fluid velocity on central axis of airway

由图12可知，加/未加遮雨帽和隔音装置时，包封线圈间气道内流体流速沿轴向方向流速分布规律基本相同，在高度的20%和80%区间范围内流速分布基本相同，由于路径选取为星形架下端，在两端位置速度为0。同时，加遮雨帽和隔音装置后，气道流速分布明显降低。

提取加/未加遮雨帽和隔音装置下气道内流体最高流速分布，如图13所示。

图13 中间位置气道内流体最高流速分布Fig.13 Distributions of the highest fluid velocity of airway in the middle position

由图13可知，未加遮雨帽和隔音装置时，各包封线圈间的流速分布及平均流速基本相同，最高速度约为1.2 m/s；加遮雨帽和隔音装置后，气道内整体流速都大幅度下降且分布不均，下降的幅度在0.3～0.6 m/s之间，且最高流速为0.8 m/s，明显低于未加遮雨帽和隔音装置的工况下，主要是由于遮雨帽与隔音装置阻碍了气道内流体的流速。同时，由于遮雨帽和隔音装置对靠近外侧的影响较大，靠近外侧包封线圈的温度较高。

综上所述，通过对比分析可知，在加遮雨帽和隔音装置下电抗器内部包封线圈最高温升不相同，其主要原因为由于隔音装置对流速的影响程度迥异，内部包封线圈温升显著增加。

4 遮雨帽和隔音装置结构参数优化设计

根据上述的分析可知，遮雨帽和隔音装置对电抗器包封线圈间气道内流体流动具有明显的阻碍作用，造成各包封线圈温升显著增加。考虑到影响电抗器温升的遮雨帽和隔音装置结构参数众多，因此，有必要开展遮雨帽和隔音装置结构参数的优化研究，以提高电抗器线圈的散热能力。

4.1 试验设计

根据加遮雨帽和隔音装置的电抗器等效模型，结合实际工程经验，确定影响电抗器温升的遮雨帽和隔音装置主要结构参数，其中影响因素总共8个，分别为遮雨帽半径x1、遮雨帽高度x2、隔音装置上端到遮雨帽底端距离x3、隔音装置顶端中心孔半径x4、隔音装置顶端与线圈顶端距离x5、最外包封线圈与隔音装置外侧的距离x6、隔音装置底端到线圈底端距离x7，隔音装置底端中心孔半径x8，如图14所示。

图14 遮雨帽和隔音装置优化参数Fig.14 Optimum parameters of the rain cover and sound arrester

考虑到电抗器实际的绝缘要求、散热和隔音效果，各参数选取的范围如下：x1的范围为1.0～1.3 m，x2的范围为0.1～0.3 m，x3的范围为0.1～0.3 m，x4的范围为0.3～0.7 m，x5的范围为0.1～0.3 m，x6的范围为0.2～0.4 m，x7的范围为0.1～0.3 m，x8的范围为0.3～0.7 m。

采用拉丁方试验设计方法[22]，可以获得试验设计表，总数为50组。结合电抗器温度场仿真计算方法，可以得到不同遮雨帽和隔音装置结构参数下的温度场仿真结果，如表2所示。

表2 拉丁方试验设计及仿真结果Tab.2 Latin square experimental design and the simulation results

由表2可知，电抗器最高和最低温度分别为109.9 ℃和81.5 ℃，因此，遮雨帽和隔音装置结构参数对电抗器的温升影响显著。根据上述的仿真结果，给出最高和最低温度的温度场仿真结果，如图15—16所示。

图15 最高温度仿真结果(样本38)Fig.15 Results of temperature distribution (case 38)

图16 最低温度仿真结果(样本7)Fig.16 Results of temperature distribution (case 7)

4.2 Kriging模型构建

Kriging方法即空间局部插值法，可根据已知数据点对未知数据点进行无偏最优估计[23]。未测点的估计值由相邻已测点加权求和求得，如式(1)所示。

(1)

式中：x0为估值点；x1，x2，…，xm为已知数据点，所得样本值相应为T(x1)，T(x2)，…，T(xm)；未测点的估值为T(x0)；μi为权重系数。

本文根据表2仿真结果建立了电抗器最高温升与结构参数间的Kriging近似模型，以反映电抗器最高温度与遮雨帽和隔音装置结构参数的响应关系，如图17所示。

图17 Kriging近似模型Fig.17 Kriging approximation model

由图17可知，随着参数x7、x8的增加电抗器的最高温度呈现逐渐下降的趋势，且参数x7下降的趋势相对于参数x8较为平缓；随着参数x4、x6的增加，电抗器的最高温度呈现先增加后下降的趋势。

4.3 灵敏度分析

为了分析遮雨帽和隔音装置结构参数对电抗器温度的影响规律，本文采用灵敏度分析技术，分析各因素对电抗器温度影响程度，其中，灵敏度指标定义为：

(2)

式中：Xi为设计变量；Y为各子系统状态变量，Var(E(Y|Xi))为E(Y|Xi)的无条件方差；Var(Y)为Y的无条件方差。

根据式(2)，可以获得遮雨帽和隔音装置结构参数对电抗器最高温度的灵敏值，如图18所示。

图18 各优化参数对电抗器最高温度的灵敏值Fig.18 Sensitivities of optimized parameters to the maximum temperature of reactor

根据灵敏度分析结果，将设计变量划分为两个层次，将敏感性指数Si>0.1划分为敏感设计变量，并将Si≤0.1划分为不敏感设计变量。因此参数x3、x4、x7和x8对电抗器最高温度的影响较为显著，其他因素影响较小。

根据近似模型数据，可以得到各参数对电抗器最高温度的影响曲线，如图19所示。

由图19可知，参数x1、x3、x5、x6和x7对电抗器最高温度的影响趋势基本相同，随着参数的增加最高温度呈先增加后下降的趋势。其中，参数x3对温度的影响最大，参数x6对温度的最小。此外，随着参数x2、x4和x8的增加最高温度大体呈现逐渐降低的趋势，且参数x4的下降趋势最快，影响最小的为参数x2。

图19 各参数对电抗器最高温度的影响曲线Fig.19 Impact curves of parameters on the maximum temperature of reactor

4.4 基于粒子群算法的优化结果

考虑到影响电抗器温度的遮雨帽和隔音装置结构参数众多，为获得最佳的结构参数，以提高电抗器散热能力，采用粒子群优化算法(partical swarm optimization，PSO)。PSO算法来源于鸟类群体活动的规律性，它模仿鸟类捕食行为，将优化问题的搜索空间类比于鸟类的飞行空间，流程图如图20所示[24 - 25]。其中，设置最大迭代次数为100、粒子种群规模为10、惯性权重为1.0、学习因子c1=c2=1.5。

图20 PSO-Kriging优化流程图Fig.20 Optimization flow chart of PSO-Kriging

基于上述的Kriging近似模型，结合粒子群优化算法PSO，获得了最佳的遮雨帽和隔音装置结构参数，如表3所示。

根据表3中的最优结构参数，在保持电抗器包封线圈电气和结构参数恒定的条件下，结合流场-温度场仿真计算方法，得到在最佳遮雨帽和隔音装置参数下电抗器温度场仿真结果，如图21所示。

表3 设计变量最优参数Tab.3 Optimal parameters of design variables

图21 最优参数下电抗器温度场仿真结果Fig.21 Temperature field simulation result of reactor with optimal parameters

由图21可知，电抗器最高温度为81.2 ℃，最高温升仅为61.2 ℃，相比于优化前电抗器的温升降低了12.4 ℃，仿真结果验证了优化方法的正确性。

5 结论

本文建立了空心电抗器流场-温度场三维仿真模型，分析了加遮雨帽和隔音装置前后电抗器的散热特性，通过优化遮雨帽和隔音装置结构参数以提高电抗器的散热能力，可以得到如下结论。

1)获得了加装遮雨帽和隔音装置前后电抗器包封线圈温升分布特点，加装遮雨帽和隔音装置后气道流体的最高流速从1.2 m/s下降到0.8 m/s，流体流速的降低造成电抗器温升显著增加。

2)将电抗器温度场仿真计算方法和拉丁方试验设计相结合，获得了不同遮雨帽和隔音装置结构参数下的温度场仿真结果，构建了Kriging近似模型，采用灵敏度分析技术，获得了不同结构参数对电抗器最高温度的影响程度。其中，隔音装置上端到遮雨帽底端距离x3、隔音装置顶端中心孔半径x4、隔音装置底端到线圈底端距离x7和隔音装置底端中心孔半径x8对电抗器最高温度影响显著。

3)根据建立的Kriging近似模型，结合粒子群优化算法获得了最佳的遮雨帽和隔音装置结构参数，在最优的结构参数下电抗器最高温升从73.6 ℃下降为61.2 ℃，优化方法能够显著降低电抗器温升。