某打浆机机架有限元分析及优化

2022-11-01安留学李丽君焦学健

农业装备与车辆工程 2022年10期

关键词：机架横梁测点

安留学，李丽君，焦学健

（255049 山东省淄博市山东理工大学交通与车辆工程学院）

0 引言

打浆机是水稻种植过程中对水田土壤进行疏松、平整的农业机具[1]。在我国该机具设计研发起步较晚，多数产品为改装、仿造成型，机器质量参差不齐，设计的可靠性和合理性难以保证[2]。

机架是打浆机的主要承载部分，使用过程中要求有较强的承载能力。在满足使用强度和可靠性的要求下，节约生产制造成本又成为制造商追求的目标。在科技高速发展的今天，借助计算机辅助设计和制造农业装备成为提高材料利用率、降低生产成本的有效手段[3]。

本文对某型号打浆机承载机架进行有限元分析，考察初始设计的可靠性，并对其进行优化改进，达到轻量化的目的。

1 建立机架三维模型

本文所研究的打浆机样机如图1 所示，其前部为旋耕轴，后部为弹齿轴。其承载机架三维模型采用SolidWorks 建立。建模的过程中对机架进行了适当的简化，去掉了机架的圆角、倒角、小孔等不重要的细小特征，最终建立的三维模型如图2 所示。

整体机架由钢板和型钢焊接而成，材料均为钢板Q235，弹性模量为210 GPa，密度为7 830 kg/m3，泊松比为0.274，屈服强度为235 MPa。

2 机架弯曲仿真及试验验证

机架各部件的厚度远小于其他方向上的尺寸，满足采用板壳单元离散模型的要求。该单元类型不仅可提高解算速度，还保证了一定的求解精度[4]。

2.1 机架弯曲变形仿真

机架是机器主要的承载件，借助梁弯曲刚度理论计算模型，将机架结构看作一根弯曲刚度均匀的简支梁，认为其在纵向平面内受力均匀，载荷沿垂向施加在简支梁的中部[5]。如图3 所示，模型以横梁长度方向为x 轴，以机器前进方向为y 轴，z 方向竖直向下。将左侧板旋耕轴安装孔x、y、z 三个方向的平动自由度约束；右侧板旋耕轴约束安装孔y、z 方向的平动自由度。侧板弹齿轴安装孔仅约束z 方向的平动自由度。施加于每个减速器支撑架上的载荷为1 470 N，尾部支撑梁上的载荷为1176 N。

经过有限元分析计算，得到该有限元模型横梁竖直方向的变形和应力结果如图4 所示。

仿真结果显示，整个机架的弯曲变形过渡平顺，没有明显的突变出现。机器后梁的变形量最大，位于横梁中心位置，最大变形量为1.59 mm。应力结果显示，最大应力出现在前梁与侧板接触焊接位置，前后横梁绝大部分应力在30 MPa 以下；中间梁的应力水平相比于前后横梁更低，应力大约在10 MPa 以下。可见，中间梁对于机架的承载作用贡献较小。

2.2 应变电测试验验证

为验证有限元模型的正确性，基于机架弯曲变形仿真情况对机架实体进行应变电测试验。应变片测量单向应力状态，应变片电阻的相对变化与粘贴应变片的试件表面上的应变比值相同[6]，即：

式中：εv——线应变；Rt——应变片的阻值；ΔRt——阻值变化量；Δl——伸长量；l——构件原长（Δl 变化十分微小，以μm 记，其长度相对变化为10-6）。

试验中选取了机架3 根横梁的8 个测点，如图5 所示。

试验过程中，为模拟机架在仿真计算中的边界条件，制作了用于固定机架的支撑框架。机架上施加的载荷采用悬挂重物的方式模拟，试验过程如图6 所示。

利用探针功能提取仿真中对应位置的应变数据与试验数据进行对比。具体数据的分析结果和仿真计算结果对比见表1。

表1 中的数据显示，除测点7 以外，测点的试验数据普遍低于仿真数据；测点2 的试验和仿真数据相差较大，其余测点数据与仿真结果较为一致，两者误差均保持在20%以内。对比各测点的数据能够说明有限元模型及计算结果的可靠性。

表1 测点应力数据对比Tab.1 Comparison of stress data of measuring points

3 机架运输状态强度分析

机架的运输状态是指机器通过三点连接固定在拖拉机尾部，随拖拉机匀速通过平坦路面时的状态。机器被拖拉机尾部的连杆举升而悬空呈45°角倾斜，仿真过程中以质量点代替各总成并耦合到机架模型上。

机架的强度校核采用第四强度理论，该理论认为构件所积累的畸变能密度一旦达到一个阈值，材料就会发生屈服破坏，与构件所受的应力状态无关[5]，此强度理论下，Von-Mises 等效应力为

式中：σ1、σ2、σ3——3 个方向的主应力；σr——Von-Mises 等效应力。

如图7 所示，根据其工作情景，固定约束机器固定架的三点连接位置。实际应用场景中，机器两侧板与两工作轴和减速器传动轴套相接触，轴和套的存在，对侧板起到了支撑和限制的作用，使得两侧板不能发生沿工作轴方向的位移，因此仿真过程中约束两侧板沿轴向的位移。运输过程中，机器整体倾斜45°，故给机器施加倾斜45°的重力加速度。为保证仿真结果可靠性，取动载系数为2。

通过计算分析，得到了道路运输情况下机器的变形、应力结果，如图8 所示。

仿真结果显示，在道路运输过程中，机架的变形主要集中在机器的尾部且靠近侧板的位置。机架的变形以固定架为中心，向两侧变形量逐步增加，最大变形量为4.50 mm。由云图可见，机架的变形过渡平滑，没有出现突变的情况。

机架的应力结果显示，机架主体绝大部分应力较小，中间梁（支撑角铁）应力水平在13.00 MPa以下，相比于前后梁，所起到的支撑作用较小。盖板尾部应力有所上升，最大应力出现在后梁与盖板接触的位置，最大值为153.17 MPa。取安全系数为1.5，则根据材料的屈服强度计算，许用应力为156.70 MPa，仿真结果小于许用应力，则机架整体满足该工况下的强度要求。

4 机架尺寸优化

在动载系数取2 时，机架运输状态下的最大变形量为4.5 mm，最大应力达到153 MPa。其中，最大变形出现在机架尾部和后梁，盖板的尾部以及两侧板的尾部都有较大的变形量。机架的最大变形量相对于机架的整体尺寸，数值较小。最大应力也小于材料的许用应力，且机架大部分结构应力数值较低，安全余量足够。因此，机架还有一定轻量化设计空间[3,7]。

在优化的过程中，将机架两侧板厚度、盖板的厚度以及前中后3 根支撑横梁的厚度作为设计变量，以仿真求得的机架形变量、机架的应力结果和机器的整体质量为状态变量。求解过程中，以机器的质量最小为目标，机架应力小于等于157 MPa 和机架整体变形量最小为约束条件，寻求各部件满足使用要求的最佳尺寸方案。经过计算，ANSYS 提供了3 组最佳优化方案，各组方案机架各结构最佳尺寸和约束条件仿真数据如表2 所示。

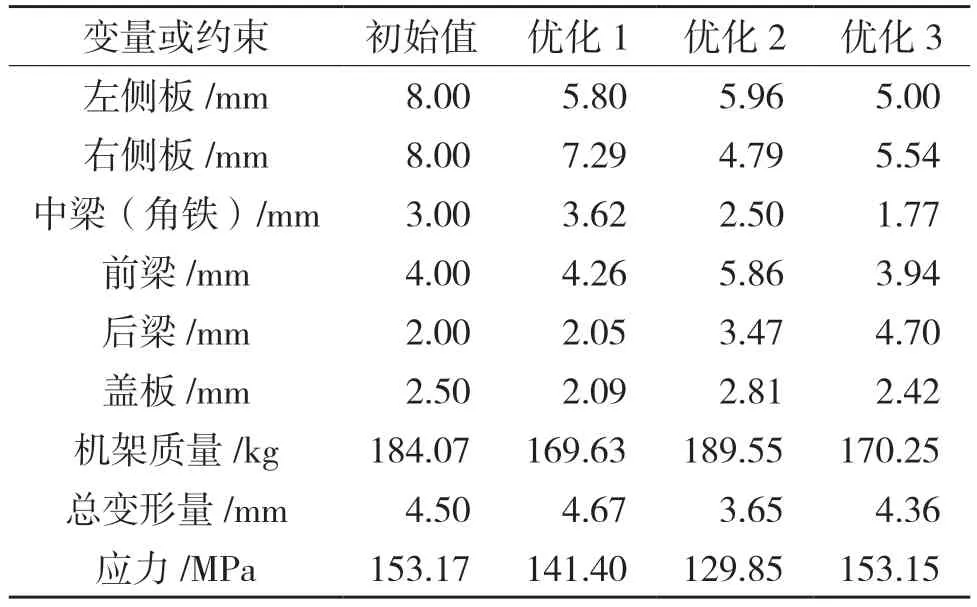
表2 优化方案数据Tab.2 Optimization scheme data

3 种优化方案均出现了左右侧板不等厚度的布置形式，为平衡机架整体变形和轻量化的矛盾，机架各部件厚度均有较大程度变化。其中，方案2 的总体变形最小，但机架质量略有增加；方案1 的整体质量和应力均有所减小，但机器的最大变形量有所增加；方案3 的质量减少量与方案1 大体相当，变形量也有所下降，应力数值也在可接受范围之内。参考标准矩形管规格，方案3 中厚度5 mm 矩形管截面尺寸较大，易与弹齿产生运动干涉。

根据对机架运输状态的仿真和试验测得的结果，中间梁应力水平很小，承载作用效果较小，考虑将其去除。结合实际情况，参考方案1 确定如下优化方案：去除中间梁，左侧板取5.0 mm，右侧板取5.5 mm，前梁厚度取4.0 mm，后梁厚度取5.0 mm，盖板厚度取2.5 mm。对优化后的模型重新进行有限元分析，得到机架的状态变量数据见表3。