基于AsyLnCPSO-SVM 的滚动轴承故障诊断研究

杨亚红，王海瑞

（650500 云南省 昆明市 昆明理工大学 信息工程与自动化学院）

0 引言

滚动轴承是各种工业机械中应用最广泛的机械部件之一，如齿轮箱、铁路轴和涡轮机。由于在恶劣的工作条件下反复轮岗，他们的健康状况趋于恶化。滚动轴承的故障诊断是防止设备故障、保证生产效率的关键，因此对其故障诊断的相关研究近年来备受关注。相关研究中，常梦容[1]等将萤火虫算法进行改进以优化支持向量机，用此方法来对轴承故障进行诊断；李平[2]等针对异步电机故障振动信号具有较强的非线性特征，而传统的线性分析方法易造成振动信号非线性成分的丢失这一情况，提出一种核主元分析和粒子群支持向量机相结合的异步电机故障诊断方法；廖力力[3]等针对大型结构振动测试中传感布置优化问题，采用改进的粒子群优化算法，实现履带车辆半车振动响应测试中加速度传感器的布置优化；王二化[4]等为了提高微铣刀磨损状态的预测精度和计算效率，提出了一种基于小波包分解和支持向量机-粒子群优化的微铣刀磨损在线监测方法；龙霏[5]等针对SDN 网络流量预测的问题，运用改进PSO 优化最小二乘支持向量机来构建网络流量预测模型。

上述模型在解决工程问题时存在诸多不良因素，主要包括模型寻优效果较低导致准确率较低；PSO 及其他改进PSO 易陷入局部最小值导致模型收敛速度慢。针对上述问题，本文提出一种学习因子异步变化粒子群优化算法优化SVM 的故障诊断模型，在提高故障诊断效率的同时，提升诊断效果。

1 粒子群的相关知识

1.1 基本粒子群算法

Kennedy 和Eberhart 在1995 年提出了一种群智能优化算法，即粒子群优化算法（PSO），是一种基于鸟群或鱼群社会行为的多智能体搜索策略[6]。它是一种迭代算法，其中个体（称为粒子）试图通过改变其位置（和速度）优化问题，随着时间的推移，根据自己的经验和邻近粒子的经验调整其位置。

在PSO 算法中，要优化问题的每个解都可以被称为一个“粒子”。每个粒子都有与它们相关的属性，如适应度值（使用目标函数计算）、位置和速度[7]。每次迭代后，粒子根据自己的经验和其他粒子的经验更新自己的位置。每个粒子位置的变化受2 个“最佳”值的影响，其中一个称为“pbest”，是当前粒子获得的最佳解决方案；另一个是全局最佳“gbest”值，是所有粒子中获得的最佳解决方案。每个质点的速度和位置更新可表示为：

1.2 学习因子异步PSO

本文构造了学习因子的非线性异步变化策略模型，使学习因子在算法迭代过程中进行动态调节，即在算法搜索初期，设置较大的c1值以及较小的c2值，在削弱粒子社会经验的同时增强粒子的自我认知，从而增加种群多样性；算法后期，c1随迭代次数的增加呈非线性递减，而c2呈非线性异步递增,逐步增强算法的全局寻优能力。具体公式为：

式中：k ——粒子当前迭代次数；kmax——最大迭代次数；η——调节参数，取值一般为正整数，主要用于调节时变学习因子的曲线变化率。

结合PSO 算法的收敛性分析，当惯性权重w从数值1.0 到0.4 线性递减时，学习因子c=c1r1+c2r2的变化范围为（0，4），即有0＜c1+c2＜4。在迭代过程中，时变学习因子c1（k）进行非线性递减，而c2（k）进行非线性递增。由此可知，若使得算法收敛，时变学习因子的上下限须满足如下条件：

实验证明，通过对学习因子上下限进行随机变化，可提升算法的收敛精度，当学习因子上下限在以及范 围内随机变化时，算法可以达到更高的收敛精度。

2 支持向量机

Vapnik 在1995 年提出支持向量网络解决分类问题，后来将其发展用于回归分析[8]。给定输入向量x 和目标数据y 的训练集 [（x1，y1），（x2，y2），（x3，y3），…，（xn，yn）]，回归函数可表示为

式中：——输出；w——权值；φ（x）——非线性函数；b——偏置。

根据结构风险最小化（SRM）原理，将结构风险函数最小化，可得到w 和b 如式（8）。

式中：c*——在模型复杂性之间进行权衡的惩罚参数；ε——目标数据y 和输出数据之间的容错范围；ξ，ξ*——松弛变量。

a 和a*拉格朗日乘数可用于解决上述优化问题[9]：

式中：s——支持向量个数；xk——支持向量；K（xk，x）——核函数。常见的核函数有

（1）多项式核函数：

（2）径向基核函数（RBF）：

（3）sigmoid 核函数：

（4）线性核函数：

3 实验

3.1 轴承故障数据说明

此次实验采用美国凯斯西储大学轴承数据中心的轴承故障数据集。数据集为12 K 采样频率下的风扇端轴承数据，分别采集正常、内圈故障、滚动体故障以及外圈故障（6 点钟方向）4 种不同状态的故障数据，除正常数据外每种状态有3 种故障深度类型，直径分别为0.177 8，0.355 6，0.533 4 mm，轴承电机载荷为0，轴承转速为1 797 r/min，总共10 类故障类别作为本次实验的数据来源。每类数据划分为115 个分类样本，10 类总共1 150 个样本。训练集大小为700 份，即每类70 份，测试集为450份，每类45 份。分类情况如表1 所示，其中RF、IF、OF分别为滚动体、内圈、外圈故障（6点钟方向）。

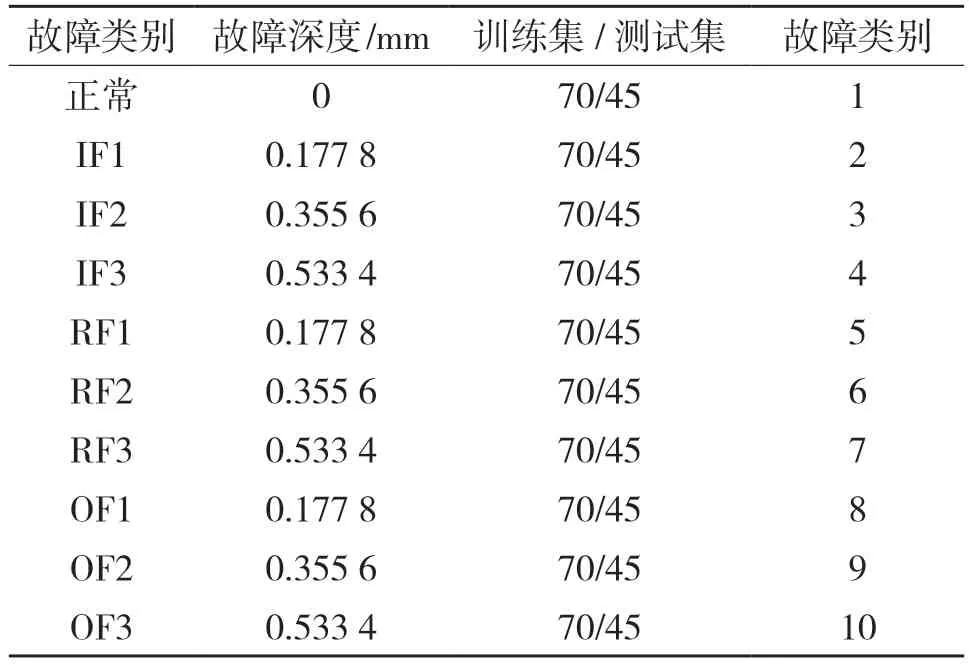
表1 轴承数据描述Tab.1 Description of bearing data

3.2 特征提取

实验特征提取，通过函数映射从原始时间信号序列提取一系列新特征。本实验每类原始时间序列总长度为117 760，将其切分为1 150 份，每份长度为1 024，分别提取每段时间序列的时域特征，并进行编号。1～10 为有纲量时域特征，分别为最大值、最小值、峰值、峰峰值、平均值、绝对平均值、方根幅值、方差、标准差和有效值；11～17 为无纲量时域特征，分别为峭度、偏度、波形因子、峰值因子、脉冲因子、裕度因子、余隙因子。

3.3 故障分类与结果分析

将上述提取到的时域特征输入到SVM 中进行训练，运用学习因子异步变化的粒子群优化算法（AsyLnCPSO）对SVM 的惩罚因子c 和核函数g进行迭代寻优。在本次实验中，设置种群规模为30，最大迭代次数为50，同时设置学习因子c1和学习因子c2非线性递增的起始下限和终止上限分别为[0.5，2.5]和[0.5，2.5],实验迭代寻优结果和分类结果如图1 和图2 所示。

经过AsyLnCPSO 算法寻优后，SVM 的惩罚因子c 和核函数g 分别为57.54 和16.72。由收敛迭代图可知，经过4 次迭代后搜索到最优值，寻优效果较好。将最优值代入SVM 中进行分类，由图可知分类准确率可达98.875%。为了对比AsyLnCPSO算法的优异性能，分别用基本粒子群算法（PSO）、线性递减权重粒子群优化算法（LinWPSO）、自适应权重粒子群优化算法（SAPSO）、随机权重粒子群优化算法（RandWPSO）、学习因子同步变化粒子群优化算法（LnCPSO）5 种优化算法对SVM 进行迭代寻优。设置迭代次数为50 次，种群数量为30。迭代寻优结果如图3—图7 所示。

可以看出，经过50 次迭代以后，原始PSO 超过了设定的迭代次数，而导致结果未收敛，效果最差；其次是RandWPSO 算法，由于权重的随机性导致寻优的不确定性，因此需要42 次迭代才能达到最优值；剩余3 种算法虽然迭代次数有所改善，但并未达到一个较好的迭代效果。可以看出本文所采取的寻优算法效果最好，仅需4 次便能寻到最优值，收敛性能远高于其他粒子群算法。表2 为几种粒子群算法最终收敛迭代次数以及准确率对比。

表2 性能对比图Tab.2 Performance comparison chart

从表2 可以看出原始PSO 准确率较低，仅为89.97%，原因是原始PSO 使得函数在设定的迭代阈值内并未收敛，未寻到最优值，从而使得准确率较低。其余几种算法虽然准确率与本文算法相接近，但收敛效果相比本文算法还存在较大差距。上述对比说明，本文所提出算法具有较大优势，相比其他算法准确率最高，可达98.87%，同时收敛效果比其它算法更好，仅需4 次便可收敛，具有较大工程应用价值。

4 结语

针对SVM 算法惩罚因子c 及核函数g 二次惩罚项α人为选取困难的缺点，提出一种AsyLnCPSO 优 化SVM 的 策 略，利用AsyLnCPSO 优异的寻优能力，使得SVM 能够高效地进行故障诊断。针对原始PSO 以及其他PSO 优化算法收敛速度慢，容易陷入局部最优的问题，提出一种学习因子异步变化的粒子群故障诊断方法。实验表明，该方法使得PSO 能够快速收敛，具有较大的故障诊断价值。