基于随机森林的公路隧道CO气体浓度预测模型
2022-11-01张志刚徐莹张锦秋韩秀杰闫尉深
张志刚, 徐莹, 张锦秋, 韩秀杰, 闫尉深
(1.河北省高速公路延崇筹建处, 张家口 075400; 2.河北工业大学土木与交通学院, 天津 300401)
隧道是公路交通网络的重要组成部分。公路隧道的建设有效地减少了道路病害、保护自然环境,提高了公路交通的运输效率。由于狭长的隧道空间不利于污染物的及时扩散,车辆排放的污染物不仅限制了隧道的建设规模,还影响隧道的运营成本、驾驶安全性和司乘人员的健康[1-2]。
一氧化碳(CO)是车辆排放污染物的主要成分,对人体健康影响最大。轻则会造成人体反应、记忆力等机能障碍;重则危害人体血液循环系统。现行公路隧道的通风控制多依据污染物监测结果实施,数据反馈的时滞性和通风控制的滞后性导致隧道内污染物浓度无法得到及时、有效的控制,极易造成隧道内污染物的积聚,从而影响人员健康和行车安全。因此,提前预知隧道内CO浓度值及其变化趋势,对隧道内CO浓度控制及隧道通风控制方案的制定十分必要。
隧道内车辆排放CO浓度受诸多因素影响,如交通量、车速、风速。已有众多学者对这些影响因素进行了研究[3-5]。陈雷[6]通过实验研究得出:无竖井纵向通风隧道越长,隧道末端CO浓度越大。雨天情况下隧道内CO气体浓度较高[7]。付伟等[8]通过物理与数学模型得出交通量与隧道长度、交通量与高程、隧道入口风速与高程对CO气体浓度的关系。《公路隧道通风设计细则》JTG/T D70/2-02—2014[9]中给出的CO排放量经验计算公式考虑了多种因素的影响。但计算公式将车速、风速等作为定值参数计算,难以作为隧道内CO气体浓度控制的依据。此外,部分学者对各因素作用下的隧道内污染气体浓度的分布特征进行了广泛研究,总结了污染气体浓度沿隧道长度的分布规律[10-11]。然而,污染气体浓度的粗略计算和定性的污染气体浓度分布规律难以作为隧道前馈式通风系统精确控制的依据,不利于实现隧道的节能环保运行。
随着机器学习的发展和推广,越来越多的学者将其应用于空气污染物浓度的预测研究[12-13]。机器学习在非线性数据处理与预测方面优势突出,Grivas 等[14]建立了基于时间和气象数据的PM10人工神经网络预测模型,模型预测结果的决定系数(R2)介于0.50~0.67。孙宝磊[15]基于污染物浓度监测数据,建立了SO2、NO2、O3、CO、PM10、PM2.56种污染物的BP (back propagation) 神经网络预测模型。王黎明等[16]提出了基于距离相关系数和支持向量机回归的PM2.5浓度预测模型。董红召等[17]利用空气污染物监测数据和车辆抓拍识别数据,构建了基于CART (classification and regression tree) 回归树的氮氧化物(NOx)浓度预测模型。构建准确、高效的隧道内污染气体浓度预测机器学习模型,实现污染气体浓度的实时预测,可为隧道通风系统的精准控制提供依据,有利于实现隧道前馈式通风系统的节能环保。
随机森林是一种灵活性高的机器学习算法,能够处理高维度数据、模型泛化能力强、训练速度快,广泛应用于交通运输[18]、水质监测[19]、电力系统预警[20]等领域,且性能突出。为准确、快速地预测隧道内CO气体浓度,降低CO气体对人员健康的危害、保证隧道营运的安全和环保,现将随机森林应用于隧道CO浓度预测研究中,并验证预测模型的准确性,以实现多因素共同作用下的隧道内CO浓度的准确预测。首先,搜集隧道内CO浓度现场实测数据建立数据库;其次,基于随机森林算法构建隧道内CO浓度预测模型;最后,将构建的预测模型应用于3 300 m长隧道的CO气体浓度预测,以验证模型的预测性能。
1 数据收集与处理
1.1 数据收集
为充分考虑各因素对隧道内CO浓度预测的影响,本文研究结合文献[4]的现场实测数据,将车流量、车速、风速作为主要输入特征。为充分考虑隧道内污染物浓度分布的不均匀性,提高模型泛化性能,将污染物监测点位置作为输入特征之一。文献[4]中实测隧道长度为2 087 m;沿隧道设置5个监测点,监测点间的隧道长度分别为360、600、540、580 m,高度均为1.2 m;测试时间共120 min;数据集共120组数据,测试日期为2019年12月20日16:30—18:30,整体分析如表 1所示。测点位置被定义为距隧道出口距离与隧道长度的比值。交通量以小客车为标准车型折算为当量标准小客车,小型车折算系数为1,中型车折算系数为1.5,大型车折算系数为2.5,汽车列车折算系数为4.0[21]。
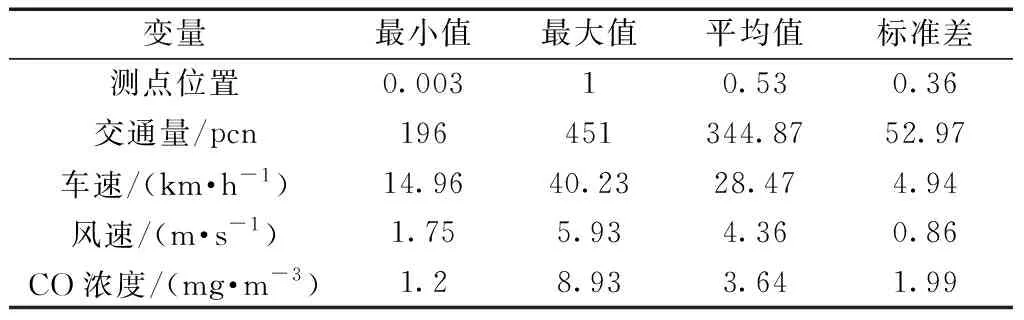
表1 样本数据集分析Table 1 Statistics of the collecting database
1.2 数据处理
皮尔逊相关系数常用于度量两个变量间的相关性,值介于-1~1。其中,-1表示完全负相关,0表示无关,1表示完全正相关。为了更好地了解各输入特征间的相关关系,避免非必要特征导致的过拟合,并减小计算强度,本文对输入特征进行皮尔逊相关性分析,计算结果如图 1所示。由图 1可以看出,各输入特征间的皮尔逊相关系数绝对值均小于0.6,各特征间为弱相关关系,因此认为各输入特征相互独立且有意义。

图1 各特征间的皮尔逊相关系数Fig.1 Pearson correlation coefficient of each pair input variables
处理数据缺失问题的常用方法为删减法和填补法。由于样本数据集数量的限制,本文采用填补法处理车速缺失数据,以减小数据缺失导致的预测误差。车速缺失数据对应的隧道限制车速为40~80 km/h,故使用[40,60]区间内的随机数填补缺失数据。
为避免数据透视差导致的模型精度虚高现象,在将样本数据集输入随机森林模型前,首先进行训练集和测试集数据的划分,并设置数据集划分随机生成器种子。数据透视差是指在模型训练过程中,由于每次划分的数据集不同,多次运行后使机器学习算法学习到整个样本数据,进而导致模型计算结果过于乐观。随机挑选数据集的70%作为训练集数据,30%作为测试集数据;随机生成器种子为42。
由表 1可知,数据集各特征值量级存在较大差异,为统一样本数据的统计分布,提高预测模型的计算效率,采用如下公式对样本数据集进行归一化处理:
(1)
式(1)中:x*为归一化后的样本数据;xmean为样本数据均值;xmax为样本数据最大值;xmin为样本数据最小值。
2 预测模型建立
2.1 随机森林模型
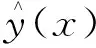
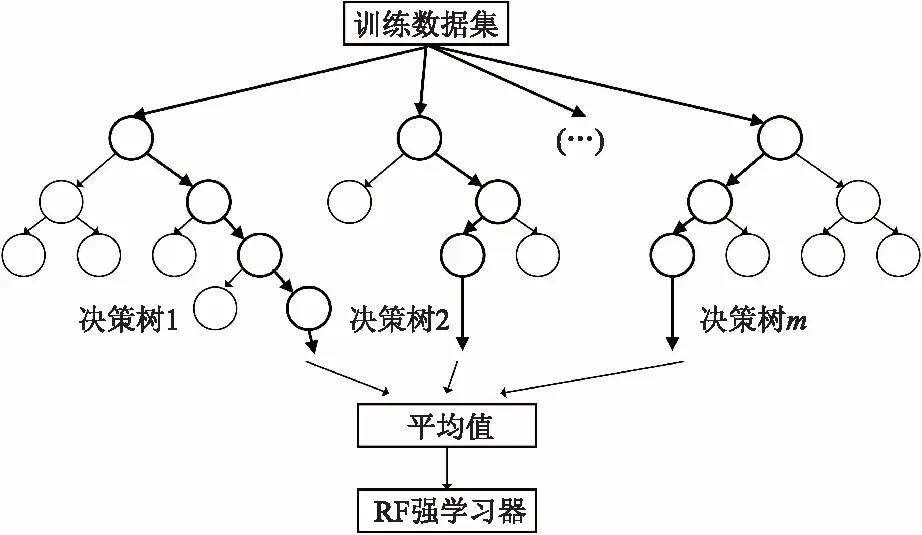
图2 随机森林原理Fig.2 Simplified conceptual diagram of the RF method
(2)
式(2)中:x为输入模型的自变量与因变量。
2.2 模型评价指标
(1)决定系数(R2),也称拟合优度,反应自变数x对变数y变异的可解释的百分比,进而判断模型的解释能力。决定系数越大,自变量引起的变动占总变动的百分比越高,自变量对因变量的解释程度越高。
(2)均方根误差(root mean square error, RMSE),也称标准误差,是观测值和真实值的差的平方与观测次数n的比值的平方根。均方根误差能够很好地反映测量的精密度。
决定系数和均方根误差的计算公式为
(3)
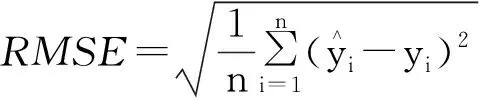
(4)
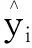
2.3 模型参数确定
随机森林是基于bagging框架的决策树模型,故随机森林的参数调节包括框架的参数择优和决策树的参数择优。采用十折交叉验证微调模型,设置30种参数组合,每种组合计算10次,组合的最优RMSE结果如图 3所示,最小值RMSE为0.491 0。据此确定最优超参数n_estimators为100;bootstrap为False;max_features为4;其余参数为默认值。
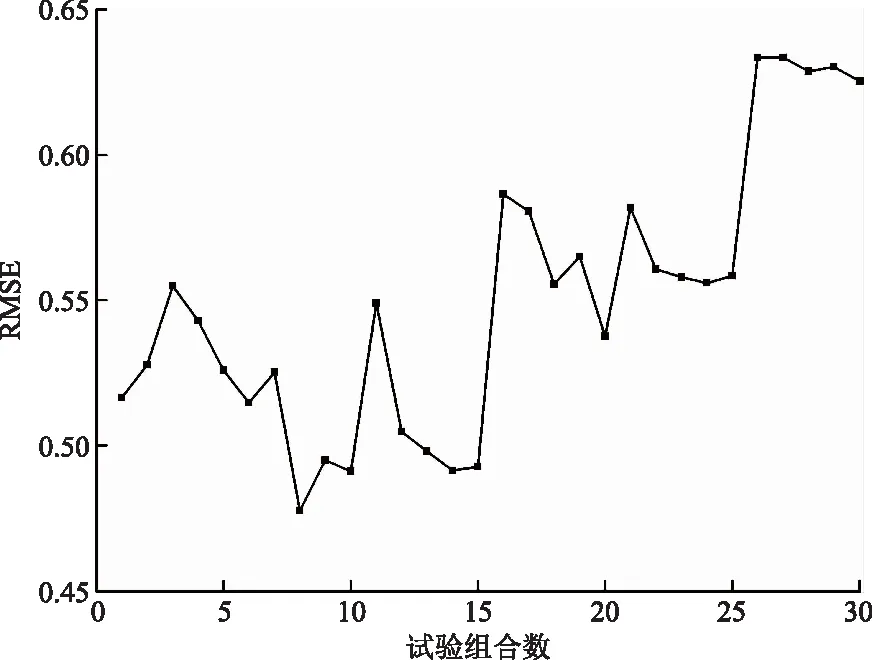
图3 每种试验组合的最优RMSE Fig.3 The best RMSE versus each parameter combination test
3 预测结果与分析
3.1 模型预测结果分析
应用预处理完成的训练集和测试集数据对模型其进行评估。模型的学习曲线如图 4所示。由图 4可知,随着训练集数量的增加,训练曲线的R2平稳至接近1。测试曲线的R2变化较大,在初始的20次循环中,R2急剧上升至0.8;逐渐趋向于训练集结果,并最终稳定于0.9左右。由此可知,CO浓度预测模型表现力好,无数据过拟合和欠拟合现象。

图4 学习曲线Fig.4 Learning curve
训练集和测试集数据应用于该预测模型的计算结果如图 5所示,其中图 5(a)为训练集预测结果,图 5(b)为测试集预测结果。由图 5可以看出,基于该模型的CO浓度预测值与CO浓度实测值十分接近。预测模型在训练集的平均绝对误差和决定系数分别为0.187 1和0.990 7;测试集的平均绝对误差和决定系数分别为0.497 4和0.943 7。由此可知,基于隧道内CO浓度影响因素构建随机森林预测模型的整体拟合性能较高,能够准确预测隧道内的CO浓度值。
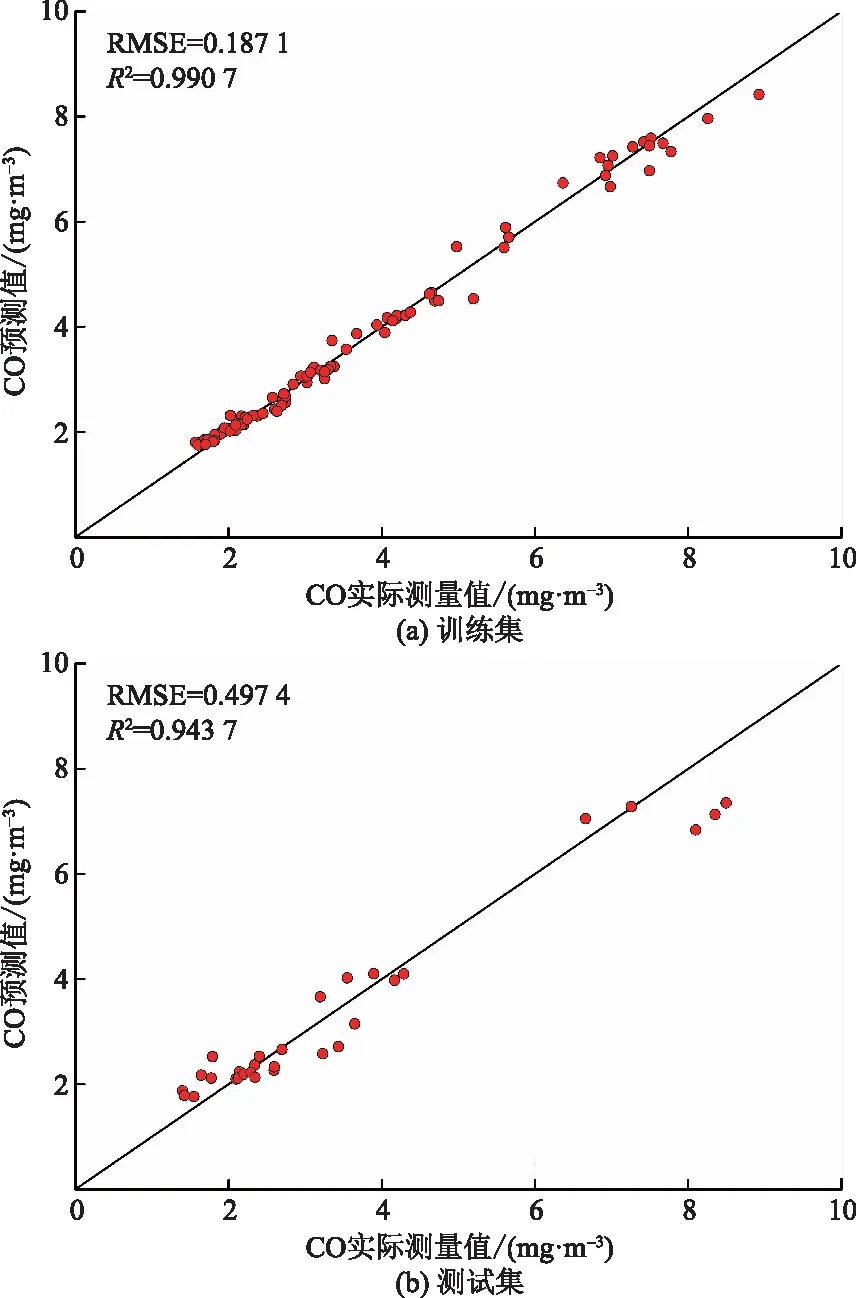
图5 预测模型计算结果Fig.5 Scatter plot of the predicted and actual pressures for full database
为进一步评估基于随机森林的隧道内CO浓度预测模型性能,本文建立了隧道内CO浓度预测线性模型和支持向量机模型,并比较3种模型的预测性能,如表 2所示。线性回归模型中训练集和测试集的RMSE分别为0.817 4和1.044 6,R2分别为0.809 7和0.778 1;支持向量机模型中训练集和测试集的RMSE分别为0.282 0和0.629 4,R2分别为0.977 3和0.919 4。RMSE值低说明预测值与真实值偏差小;R2高说明预测值与真实值接近,模型拟合效果好。由此可知,随机森林模型的测试结果优于线性回归模型和支持向量机模型。
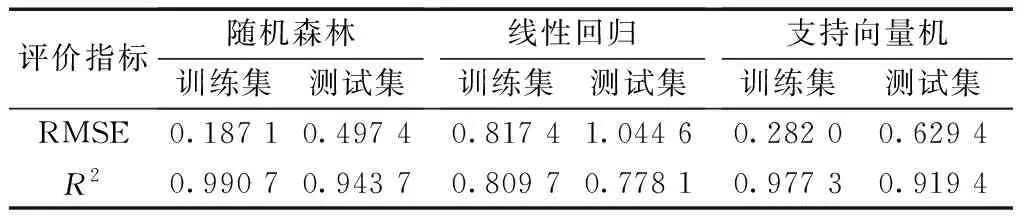
表2 随机森林和线性回归模型性能比较Table 2 The performance comparison of random forest and linear regression
3.2 预测模型验证
将构建的隧道内CO气体浓度预测模型应用于3 300 m长公路隧道内CO气体浓度预测,并将预测结果与实际CO气体浓度值比较,进一步验证预测模型的适用性。验证集数据来源于整理文献[4]中关于3 300 m长隧道的实测数据(共110组)。数据采集监测点为5个,间距为900、770、610、510 m,监测点高度为1.2 m。现场实测时间为2020年1月9日17:10—19:00。数据的统计方式与表 1相同,两次隧道实测仪器相同。数据集分析如表 3所示。
将验证集数据输入特征按照式(1)进行归一化处理后导入训练好的CO预测模型,并将模型输出结果与验证集CO浓度真实值进行对比,结果如图 6所示。验证集的RMSE和R2分别为0.909 5和0.729 5, 劣于测试集数据计算结果。这是由两组实测数据集的数据差异导致。两组实测数据来自不同的隧道,表 1中数据源于隧道A,长2 087 m,单洞建筑限界宽度为13.25 m,限高为5 m,设计速度为80 km/h;表 3中数据源于隧道B,长3 300 m,单洞建筑限界宽度为8.5 m,限高为4 m,设计速度为50 km/h。表 1数据集中交通量和车速数据的标准差分别为52.97和4.94,而表 3验证集数据中交通量和车速数据的标准差分别为32.78和14.71。两组数据中交通量和车速数据的标准差相差约37.78%和197.78%,这使得预测模型在验证集预测性能的表现稍差。此外,隧道A与隧道B所处地理位置存在差异,会导致环境中的CO气体浓度略有不同,而实测数据为考虑隧道环境的CO气体浓度,而CO气体浓度预测模型是基于隧道A的测试数据建立,因此导致预测模型对隧道B内CO气体浓度的计算误差。
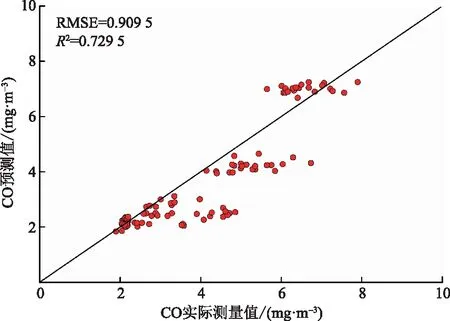
图6 模型验证结果Fig.6 Scatter plot of the predicted and actual pressures for validation database
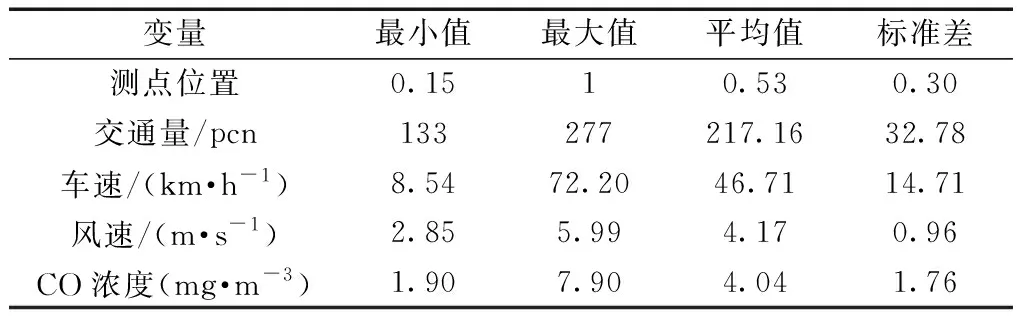
表3 样本数据集分析Table 3 Statistics of the collecting database
总体而言,基于2 087 m隧道现场实测数据建立的CO浓度预测模型能够较为准确地预测CO浓度,模型泛化能力较强。
3.3 特征重要性分析
为进一步分析各输入特征对隧道内CO浓度预测的影响,应用随机森林对输入特征的重要性进行分析,并采用基尼指数作为特征重要性评价指标。依据特征重要性评分结果将各特征依次排序,如图 7所示。由图 7可以看出,测点位置的重要性评分最高(0.593 34);其次是风速(0.330 14);车速和交通量的重要性评分分别为0.045 26和0.031 26。
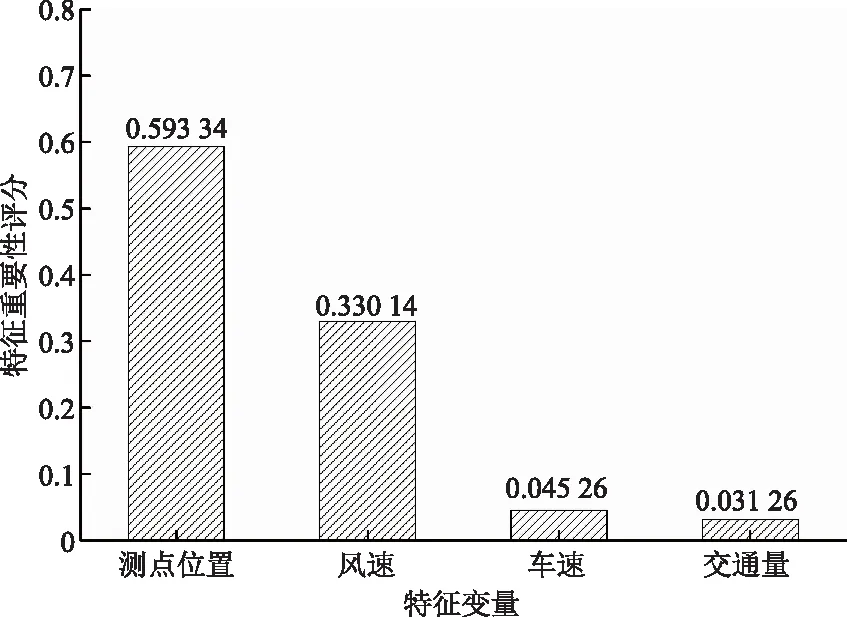
图7 特征重要性Fig.7 Feature importance
特长隧道内CO浓度监测点位置间距较大,不同监测点CO气体浓度存在差异,致使隧道内CO气体浓度分布不均匀。因此,测点位置对特长隧道CO气体浓度预测有较大影响。图 8为各输入特征与CO浓度的散点图,图8中红色线段为对应特征与CO浓度的关系曲线。由图 8可以看出,测点位置与CO浓度的关系最为显著[图 8(a)];风速与CO浓度的关系拟合曲线[图 8(b)]次之。随着测点位置值的增大,隧道内CO浓度逐渐减小,即靠近隧道出口处,CO浓度值较大。此外,隧道内CO浓度值随风速的增大逐渐减小。车速、交通量与CO浓度的关系难以通过数据散点图总结[图 8(c)和图8(d)],因此,车速与交通量对隧道CO浓度的影响规律的总结应结合其他因素综合考虑。
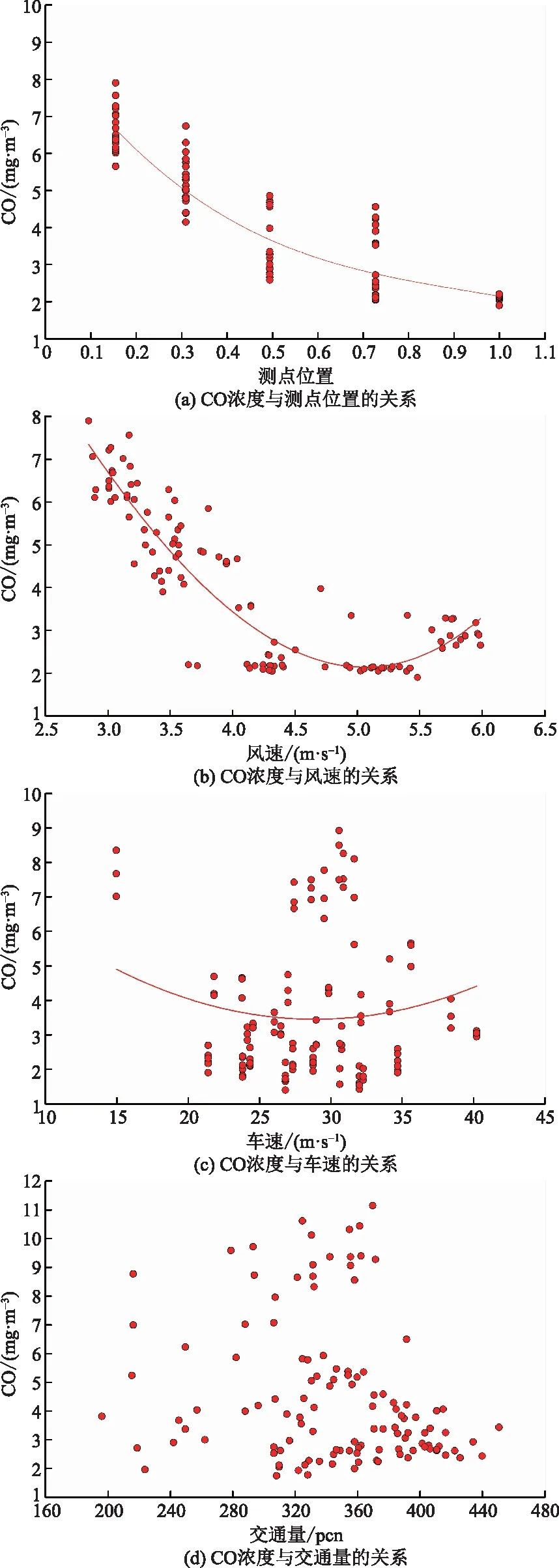
图8 输入特征与风速的关系Fig.8 Scatter plot of CO versus input variables
4 结论
(1)以公路隧道实测数据为基础,建立了以交通量、车速、风速为主要输入特征的特长隧道内CO气体浓度预测模型。该模型在训练集的RMSE和R2分别为0.187 1和0.990 7;测试集的RMSE和R2分别为0.497 4和0.943 7;预测结果优于线性模型和支持向量机模型。
(2)本文建立CO气体浓度预测模型具有准确的预测性能和良好的泛化能力。预测模型应用于3 300 m长隧道内CO气体浓度预测,预测结果与实际CO气体浓度值比较显示RMSE和R2分别为0.909 5和0.729 5。
(3)特征的重要性分析确定测点位置对隧道内CO浓度的影响最大,风速次之。随着测点位置值的增大,隧道内CO浓度逐渐减小;靠近隧道出口处,CO浓度值较大。隧道内CO气体浓度值随风速的增大逐渐减小。
