基于ANSA 的轿车前车门水切刚度分析

郑竹安，魏金呈，郑精干，梁仓

（224051 江苏省 盐城市 盐城工学院 汽车工程学院）

0 引言

车门是车身上的一个相对独立又重要的总成，它对汽车的安全性和舒适性都有非常大的影响[1-2]。车门担负着在汽车行驶中对车内乘员的保护重任，其本身刚度要求很高，同时针对不同位置的刚度，其要求也大相径庭。车门水切部位的刚度与车窗和车门的密封性能息息相关，所以对于设计研发者来说，车门系统的水切刚度和强度是否足够，是实验研究中非常值得关注的问题[3-4]。本文基于ANSA和Nastran 等有限元分析以及前后处理软件，对车门系统的整体进行建模，并对其钣金件的水切安装部位的刚度进行了系统的分析研究[5]。

1 刚度计算过程中的接触问题

经典的Hertz 理论是接触问题解析解的基础，为了将它和数值解作比较，现将经典Hertz 理论以两个最具代表性的球体接触为例进行简单介绍[6-8]。球体接触如图1 所示。

图1 球体接触示意图Fig.1 Schematic diagram of sphere contact

下球体的半径为R1，上球体的半径为R2。当2 个球体之间不施加载荷力时，2 个球体的接触点为O，该点实际上处于接触的临界状态，也是二者之间没有应力的初始状态。此时假定2 个边缘点为M1、M2，这2 个点与O1和O2连线的距离为r，与上下球体的公共切面的垂直长度分别为Z1、Z2。

如果M1和M2很靠近O点，则

上下球体之间加压后，假设O点周围局部地区产生了一个圆形接触区域。设M1沿Z1方向的位移为ω1，M2沿Z2方向的位移为ω2，其中ω1、ω2都是压缩变形。设在Z1轴和Z2轴上远离O的2 点其应变可忽略不计。并设2 点之间的间距缩短量为Δ，则当M1和M2已经相互靠近而变为一点时，根据几何关系可得：

弹性半空间体受圆面积载荷时，弹性半空间体受载荷区表面法向位移的公式为

式中：μ——泊松比；E——杨氏模量；q——接触区域载荷分布函数；s——接触区域。

2 刚度分析的求解过程

本文涉及的仿真计算过程主要是隐式求解，求解过程如下。

静态平衡的基本表达式为：由单元应力引起的加在节点上的内力I与外力P必须平衡，即：

求解该方程，需使用牛顿迭代法求近似解[9]。第一次迭代时（i=1），假设初始收敛增量的解u0和P0是2 个已知的数值。在当前增量步中，首先把一个小的增量加载力P施加到结构上。软件基于u0处的切线刚度K0确定位移的修正值c1。软件更新模型的状态为u1，计算出新的刚度值K1，同时计算I1。预期完整加载后的总加载力PTOTAL与当前加载步得到的内力I1的差值称为残差R1。如果R1在模型的每个自由度上都非常小（在软件允许的误差范围之内），此时结构就是平衡的。默认的误差范围是在整个时间段上对结构进行完整加载的平均力的0.5%。

在迭代过程中，软件会自动计算某一空间和时间上的平均力。如果满足要求，则称该计算收敛，得出结果。如果该次计算结果不能满足要求，就称不收敛，自动执行另外的迭代计算。初始迭代如图2 所示。

图2 初始迭代Fig.2 Initial iteration

第2 次迭代（i=2）计算时，会基于新得到的刚度值K1计算新的位移修正值c2，且K1C2=PTOTALI1=R1，此时可以得到新的残差R2=PTOTAL-I2。将新的残差R2和软件设定好的误差范围进行对比，检验能否得到符合要求的结果[10]。整个迭代计算过程会一直循环进行，一直等到某一次结果的残差能够小于系统允许的误差为止。每次迭代i需要形成切线刚度Ki。求解系统方程组，得到位移修正ci+1。修正位移的估计值：ui+1=ui+ci+1，基于ui+1计算内力向量Ii+1。进行平衡收敛判断：

Ri+1是否在容差之内，是否。

二次迭代如图3 所示。

图3 二次迭代Fig.3 Second iteration

3 车门水切刚度的模拟计算

3.1 车门模型的建立

在实际问题中，分析的物体结构往往十分复杂，通过计算模型模拟实际工程问题的误差（离散误差）要比有限元仿真分析的计算误差大得多。根据圣维南原理[11]，模型的局部微小变动对模型总的计算分析结果的影响几乎可以忽略不计，所以可对车门模型做如下简化：（1）建模时略去喇叭、升降机、升降机把手、车门把手等对车门结构和应力分布的影响可忽略不计的车门附件。（2）简化截面形状，对距离较近且作用基本相同的部件合为一个，适当简化截面形状。（3）为保证网格趋势顺滑，建模时要让构件表面光滑平顺，部分凸台、线路孔、销孔可适当忽略。

对车门进行以上简化处理之后，就可以使用CATIA 软件建立车门系统的三维实体模型，然后将模型导入ANSA 进行几何信息的清理和结构的离散化（网格划分），如图4、图5 所示。

图4 局部网格示意图Fig.4 Local grid diagram

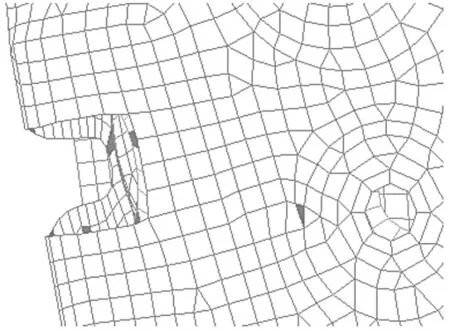
图5 局部网格示意图Fig.5 Local grid diagram

3.2 加载和边界条件

3.2.1 加载的设置

加载位置涉及车门4 个钣金件，其材料及属性如表1 所示。

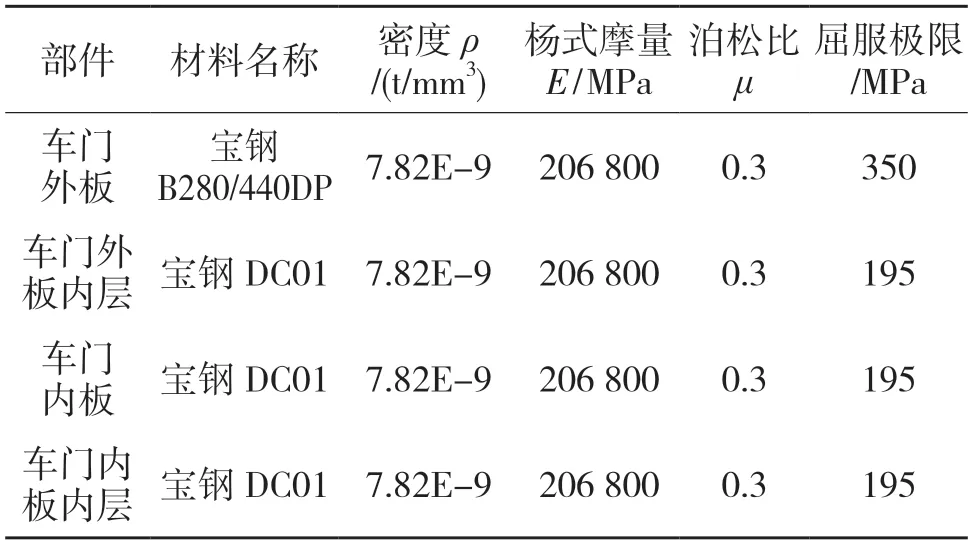
表1 加载部件材料表Tab.1 Material list of loading parts

部件位置图见图6、图7。

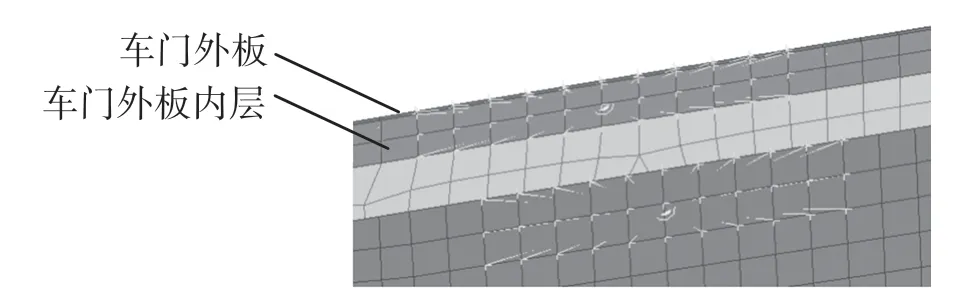
图6 加载区域示意图Fig.6 Schematic diagram of loading area

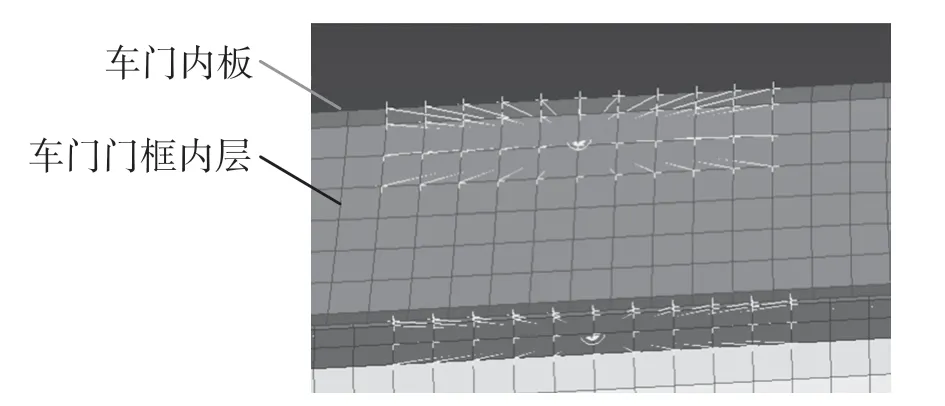
图7 加载区域示意图Fig.7 Schematic diagram of loading area

考虑到材料的屈服极限和属性，加载区域设置为车门门框下端正中心长约50 mm 的长方形区域，如图8 所示。

图8 加载区域示意图Fig.8 Schematic diagram of loading area

加载方式为，用刚性单元抓住加载区域的网格，在刚性单元的中心节点上施加单点力加载，加载方向为垂直加载区域平面向玻璃安装方向，加载大小F=100 N，如图9 所示。

图9 加载力Fig.9 Loading force

加载时，由于加载区域平面并不和主坐标系的坐标基准平面平行，所以必须建立局部坐标系，使得加载力可以通过引用局部坐标系来校准方向，让加载力可以垂直加载区域平面，满足分析的加载要求。

3.2.2 边界条件的设置

边界条件的定义，就是求解区域的边界上需要求解的变量或者它的导数随时间和地点的变化而发生变化的规律[12]。在进行机构仿真计算过程中，如果想要控制方程得到确定解，获得真实恰当的数据，核心步骤之一就是要设定好边界条件。而在所有有限元法的分析计算项目中，几乎所有问题的求解都需要设置好边界条件[13]。处理好边界条件的必要性在于模型中边界条件的合适与否，不仅决定了计算结果是否足够精确，而且在很大程度上决定分析的走向和结果[14]。

在本文分析中，边界条件的直接表现就是车门的约束点。分析需要建立的约束分为2 个区域，一是铰链位置的约束点，二是锁点约束。

（1）铰链约束相对简单，此处的约束主要是模拟车门安装在汽车上的情形，也就是将与车门铰链相连接的车身铰链的安装孔固定住，保证在加载力工作时，车门处于稳定状态。

具体约束方法是，使用刚性单元抓住铰链安装孔，并在刚性单元的中心节点建立SPC 约束，限制该安装孔安装位置的x、y、z、Rx、Ry、Rz全部6个自由度，因为安装位置的所有自由度都被约束并且没有其他的特殊设置，所以不需要在这个位置引用局部坐标系，直接引用全局坐标完成设置。铰链及自由度如图10 所示。

图10 铰链及自由度Fig.10 Hinge and degree of freedom

如图11 所示为车门与车身连接在一起所用的下铰链组（单独显示），单个车门与车身之间共有2 个铰链组，上下均匀分布。铰链组由Kenamatic连接模拟铰链工况，Kenamatic 连接需要在铰链组的2 个铰链之间设置，且引用局部坐标系，释放2个铰链之间上下连接孔中心点连线代表方向的旋转自由度，限制其他5 个方向的自由度。在该模型的建立中，由于局部坐标系的z方向与两铰链的中心点连线方向相同，故Kenamatic 连接释放Rz自由度，约束x、y、z、Rx、Ry自由度模拟铰链的实际工况。

图11 铰链转动副示意图Fig.11 Schematic diagram of hinge rotation pair

图12 所示即为局部坐标系和铰链中心点连线方向对比与Kenamatic 连接的设置。

图12 铰链转动副参数Fig.12 Hinge rotation pair parameters

（2）锁点约束相对复杂。锁点在本项分析中定义为锁扣与锁孔组合后的最终接触点（理想化定义），通过使用刚性单元抓住锁孔上下的2 个安装孔，模拟车门门锁的实际情况，刚性单元的主节点即为锁点，所以锁点约束指的就是在锁点位置进行边界条件的定义，控制锁点处的一定自由度。

由于本次分析的是车门在日常生活情况（正常工作）下的水切刚度，即车门必须要处于关闭状态的情况下。为了模拟这种情况，锁点所在锁孔区域需要保证的自由度标准是，锁孔必须保证无法进行3 个方向的平动，同时锁扣的横切面始终与锁孔的横切面相平。为了完成这个目的，锁孔的横切面必须被约束，而锁孔的横切面又不与总坐标系的基准面相平行，所以需要设立局部坐标系，且局部坐标系的一个基准面要与锁孔的横切面平行。同时，引用该局部坐标系，约束锁点位置的某3 个平动自由度，同时留出3 个旋转自由度模拟现实的情况（锁扣和锁扣略有活动）。锁孔截面如图13 所示，锁点截面如图14 所示。

图13 锁孔截面Fig.13 Keyhole section

图14 锁点Fig.14 Lock point

图15 所示为锁点约束在模型中的设置情况。

图15 锁点参数Fig.15 Lock point parameters

3.3 输出设置

完成上述设置后，可以完善接触设置，输出模型并利用求解器计算。Nastran Header 是模型搭建完成后需要求解计算时设置的先导文件，通过设置Nastran Header，让求解器求解出需要的数据和结果。本次分析使用SOL400 进行隐式非线性分析。参数设置如图16 所示。

图16 Nastran Header 参数设置Fig.16 Nastran Header parameter settings

4 后处理与结果分析

由于上文对车门框下端水切安装点位置的钣金件的加载力并不大，所以只需对计算结果进行一般性的强度和塑性破坏考量，主要是受力点的位移、车门整体钣金的塑性变形以及加载钣金的Von Mises 应力数值（剔除被连接和刚性单元抓取的部分）。具体标准见表2。

表2 分析标准Tab.2 Analysis criteria

首先，需要读取加载点位移。位移云图如图17 所示，车门外板水切安装处加载区域的最大位移为1.38 mm，表2 中，外板加载点位移必须小于1.75 mm，结果符合分析要求，材料的使用和结构强度满足预期。

图17 位移云图Fig.17 Displacement nephogram

仅读取外板加载区域的位移不够完善，还需读取内板加载区域加载点的位移，提高分析的精确性。

由图18 位移云图可以看出，车门内板水切安装处的加载部分的最大位移是1.16 mm，由表2 可知，内板加载点位移必须小于1.5 mm，结果符合分析要求，材料和结构满足预期。

图18 位移云图Fig.18 Displacement nephogram

在完成位移结果的读取之后，还需要对车门的塑性变形进行整体的检验。根据分析标准，整体车门的塑性变形必须小于0.2%，读取结果如图19所示。由图19 可知，整体车门在加载力的作用下塑性形变为0，完全满足分析标准。

图19 塑性变形云图Fig.19 Plastic deformation nephogram

除以上分析项外，还需对钣金件的Von Mises应力进行分析，读取结果如图20 所示。

图20 Von Mises 应力云图Fig.20 Von Mises stress nephogram

由图20 可见，在2 个加载力下的2 个Subcase中最大的Von Mises 应力为132.631 MPa，上文加载区域涉及到的钣金件为车门外板、车门外板内层、车门内板、车门门框内层，这4 个钣金件所使用的材料中，屈服极限最低的材料是宝钢DC01，屈服极限值为195 MPa，远高于加载区域涉及到的钣金件的Von Mises 应力，所以满足要求。

5 结论

在汽车的设计与研发过程中，使用软件对汽车本体及零部件进行仿真分析，可以预知汽车在开模实验甚至未来生产销售可能会遇到的问题，提前避免这些问题，就能有效地减少人力物力损耗，降低生产成本，从根本上提高生产效率，通过各种性价比的提升，为研发生产公司提高竞争力，也能使顾客有良好的消费体验。

本次车门水切的结构仿真分析结果显示，基于本文材料的该结构下的车门系统具有良好的刚强度和抗塑性变形能力，不存在预期外力下的塑性变形甚至结构破坏的可能，车门系统的结构和材料满足要求，车窗的密封性能也足以满足日常使用所需。

车门水切刚度部分的结构简单，但是其中涉及到了比较复杂的结构理论和刚度、强度理论，而本文车门系统的设计完全满足检验标准，能够很好地契合整车设计研发的需求，可以开始进行下一阶段的实际检验。