自复位两边连接梯形波纹钢板剪力墙滞回性能分析

谭志伦，赵秋红, 2

自复位两边连接梯形波纹钢板剪力墙滞回性能分析

谭志伦1，赵秋红1, 2

(1. 天津大学建筑工程学院，天津 300350；2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300350)

本文提出了一种自复位两边连接梯形波纹钢板剪力墙结构，包括自复位钢框架与内嵌梯形竖波纹钢墙板，其中墙板仅与梁上下连接，以方便装配化施工．采用通用有限元软件ABAQUS建立了单层单跨自复位梯形波纹钢板剪力墙的有限元模型，并进行非线性滞回分析，以研究墙板连接形式、墙板波形及框架预应力水平对结构滞回性能和复位性能的影响．结果表明：自复位两边连接梯形波纹钢板剪力墙可有效耗散地震能量，控制震后残余侧移，且侧边加劲时两边连接墙板的承载力、耗能能力及残余侧移与角部切角时四边连接墙板基本相当．随着厚度的增加，两边连接波纹墙板的抗侧模式由剪切屈曲向剪切屈服转变，结构承载力及单位板厚的耗能能力显著增加，当板厚从3mm增至9mm时增幅分别为40%和50%，但结构残余侧移亦显著增加，2%侧移角下的残余侧移角可能超过规范可修限值的0.5%．随着波纹墙板波折角或波长的减小，结构残余侧移可有效降低，但结构承载力及耗能能力亦有所降低，最高可分别达30%和60%．另一方面，随着预应力筋的初始预应力增加50%，结构承载力增加13%，最大残余侧移角显著降低，由0.80%减小到0.35%，而耗能能力基本不变．随着预应力筋面积的增加，结构承载力增加，但残余侧移和耗能能力基本不变．因此，两边连接波纹墙板的屈曲及抗侧模式对自复位波纹钢板剪力墙结构滞回和复位性能的影响较为明显，且与传统波纹钢板剪力结构不完全一致，自复位两边连接波纹钢板剪力墙初期设计时应综合考虑墙板波形与框架预应力水平对结构滞回及复位性能的影响，使结构充分发挥承载力和耗能能力，并有效控制震后残余侧移．

自复位梯形波纹钢板剪力墙；两边连接；滞回分析；有限元参数分析；抗震性能

钢板剪力墙结构是20世纪70年代发展起来的一种新型抗侧力结构体系，主要包括边缘钢框架和内嵌平墙板．钢板剪力墙结构具有较高的承载力、延性及稳定的耗能能力，在多高层住宅结构中得到广泛应用[1-3]．地震作用下，钢板剪力墙中的内嵌平墙板作为主要抗侧力构件形成对角拉力带并屈服，随后梁端和底层柱底形成塑性铰，具有良好的变形及耗能能力；但与此同时，结构亦会产生塑性损伤和较大的残余侧移，影响震后修复及功能恢复．

为减少钢板剪力墙结构的残余侧移、实现震后功能快速恢复，Berman等[4]将采用预应力筋的自复位钢框架替代边缘钢框架，形成自复位钢板剪力墙(SC-SPSW)，其中平墙板在侧向力作用下通过拉力带屈服耗能，而梁柱构件基本保持弹性，并通过预应力筋提供复位力．Clayton等[5-6]针对SC-SPSW提出了基于性能的抗震设计方法，且发现框架节点张开后，结构抗侧刚度下降明显，侧移较难控制. Winkley[7]和Clayton等[8]设计了4个两层单跨SC-SPSW并进行了拟静力试验研究，结果表明试件残余侧移较小，可以满足相应性能目标，但梁柱节点转动角度高于普通钢板剪力墙，墙板角部易撕裂．因此，Clayton等[9-11]将SC-SPSW的墙板只与边框梁连接，并进行了拟静力试验研究，结果表明墙板角部撕裂虽有所延缓，但结构承载力及抗侧刚度明显降低．

国内学者徐基磊等[12]提出了自复位两边连接蝴蝶型剪力墙及开菱形缝钢板剪力墙，Lu等[13]提出了自复位两边连接开竖缝钢板剪力墙，并进行了拟静力试验研究与数值模拟，结果表明墙板开缝有效提高了结构的延性和变形能力，但刚度和承载力有一定削弱．Wang等[14]对装配式自复位开缝钢板墙模块进行了拟静力试验研究，结果表明，结构复位性能较好而耗能能力适当．周林丽[15]和谭平等[16]提出了自复位半圆形波纹钢板剪力墙，并进行了拟静力试验研究，结果表明半圆形波纹墙板的屈服先于屈曲发生，且小直径试件的极限荷载、屈服荷载及耗能均优于大直径试件．

值得注意的是，国外学者提出的SC-SPSW基于性能的抗震设计方法中，大震下目标层间侧移角为4%[5]，但这与我国抗震规范[17]中大震下钢结构层间侧移角不可超过2%的要求相矛盾．在重力或较低侧向力作用下，平墙板易发生弹性屈曲，抗侧刚度随之明显下降，这也导致SC-SPSW结构抗侧刚度较低，侧移较难控制，当墙板仅与边框梁连接时尤为明显．若将平墙板通过轧制或弯折的工艺制作为梯形波纹墙板，可极大提高墙板的弹性屈曲承载力及柱面刚度，避免在施工及正常使用阶段产生屈曲及面外变形.与此同时，波纹肋沿水平方向的墙板(简称横波板)由于风琴效应的存在可有效规避重力，而波纹肋沿竖直方向的墙板(简称竖波板)由于柱面刚度显著增加可有效抵抗重力，提高施工效率[18-19]，且墙板表面部分为平面，易与边框及隔墙连接．目前，梯形波纹板已在工业厂房、桥梁及钢板剪力墙结构中得到应 用[20-25]，在我国亦有数条成熟的生产线．

因此，本文提出了自复位两边连接梯形竖波纹钢板剪力墙，以避免墙角过早撕裂，提高自复位钢板剪力墙结构的承载力及抗侧刚度，并有效控制层间侧移．通过有限元非线性滞回分析及参数分析，探究了墙板连接形式、波纹墙板几何参数与预应力水平对结构滞回和复位性能的影响规律，以促进工程应用．

1 体系构造及简介

1.1 波纹钢板

本研究采用的墙板为梯形波纹钢板，其截面形式和几何参数如图1所示，其中为波纹板高，为波纹板宽，为波高，为波折角，为波长．

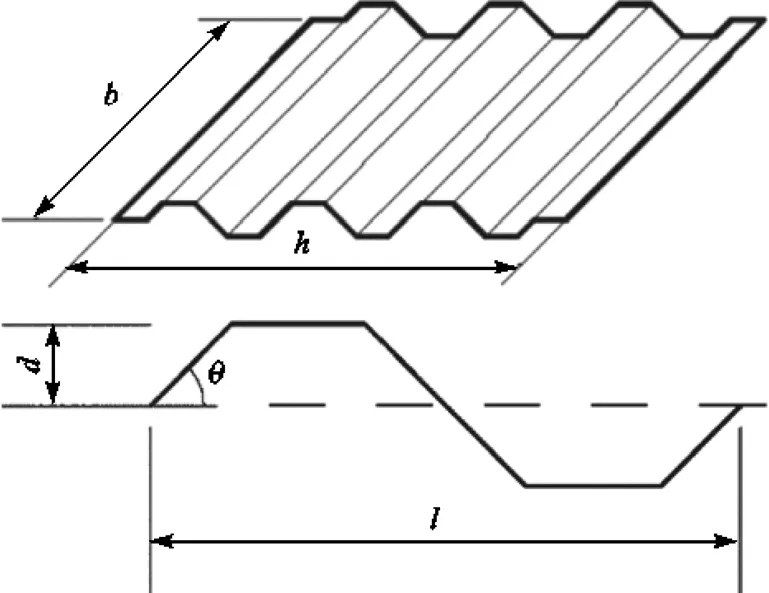
图1 梯形波纹钢墙板示意

1.2 自复位钢框架

自复位钢框架由边框构件和后张预应力筋组成，其节点构造如图2[8]所示．通过后张预应力筋将梁柱节点连接在一起，使节点在张开前具备近似于传统刚接框架的抗弯刚度，并在梁腹板与柱之间设置剪切板以传递剪力．在楼层侧向力作用下，梁一侧翼缘压力逐渐增加，另一侧翼缘压力逐渐减小至0，梁端部截面沿一侧翼缘开始发生转动，节点张开，此过程称为梁柱节点解压．随着梁柱间转角的增加，预应力筋逐渐伸长，产生的弹性恢复力为结构提供了复位能力，但节点抗弯刚度相比解压前有所降低．

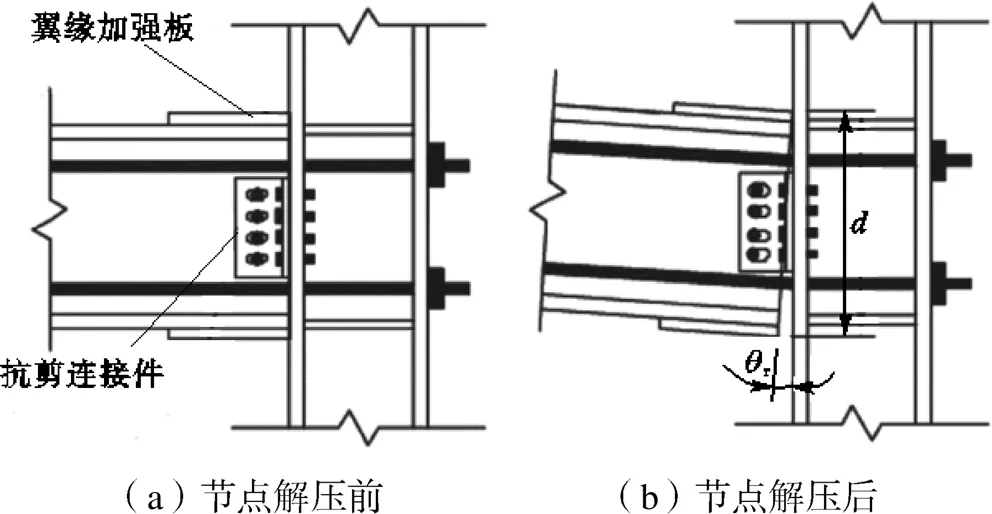
图2 自复位钢框架节点示意

1.3 自复位两边连接及四边连接波纹钢板剪力墙

自复位两边连接波纹钢板剪力墙构造如图3(a)所示，其中竖向梯形波纹墙板与边框柱间留有门洞，并在墙板两侧设置加劲肋，墙板与加劲肋上下端通过鱼尾板与边框梁焊接．作为参考，亦建立了自复位四边连接波纹钢板剪力墙的有限元模型，构造如图3(b)所示，其中墙板角部切角以避免撕裂，切角长度与梁高相同[6]．自复位两边连接及四边连接波纹钢板剪力墙的边框尺寸、预应力水平、墙板厚度、波形及波纹边锚固长度均相同．

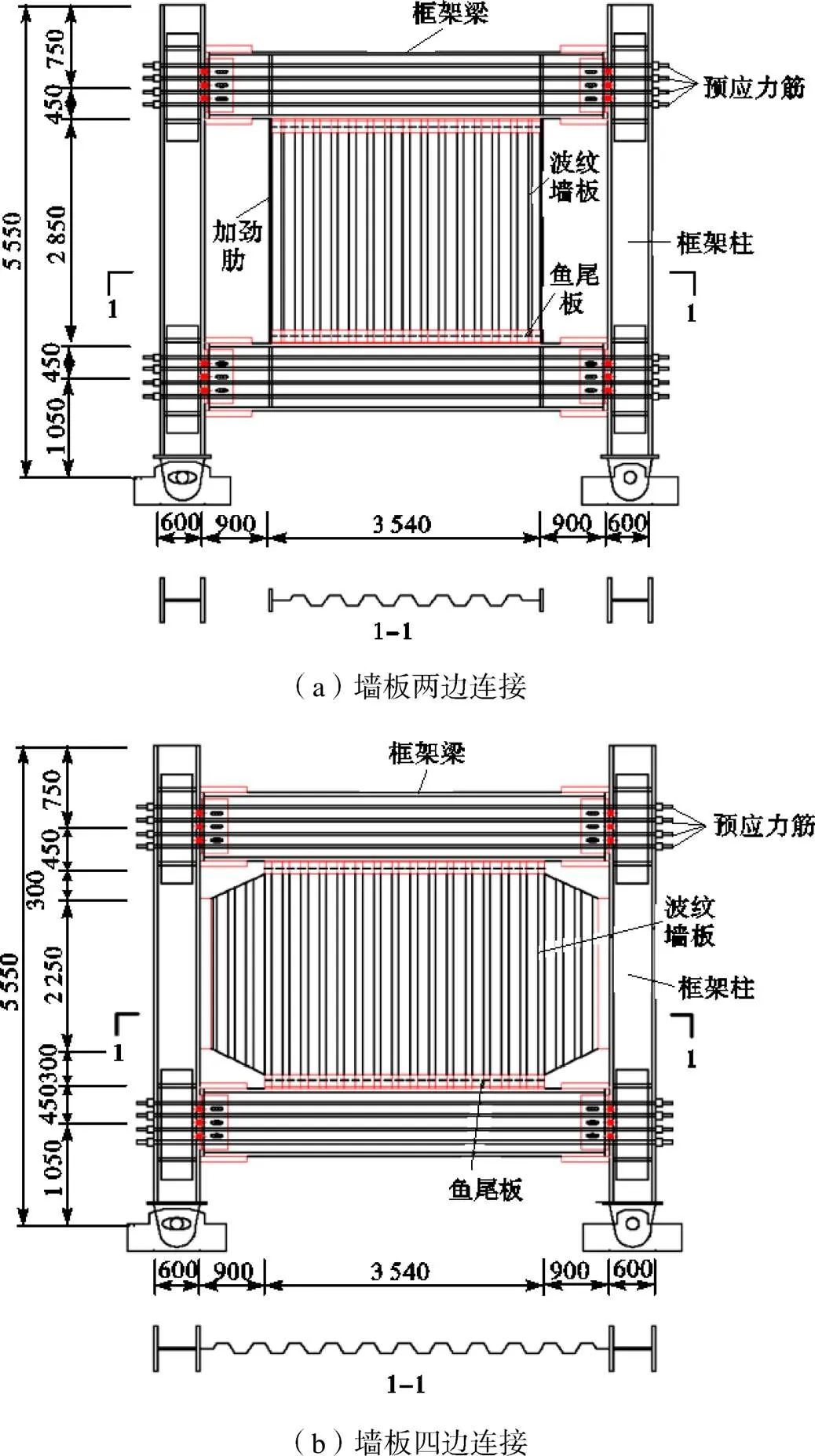
图3 自复位波纹钢板剪力墙构造

2 有限元分析

2.1 模型参数设置

本文采用有限元软件ABAQUS对12个单层单跨自复位波纹钢板剪力墙模型进行了滞回分析，其中1个模型为四边连接墙板，其余模型为两边连接墙板．模型变化参数包括板厚、波折角、波长、初始预应力和预应力筋面积，命名规则为“C板厚-波折角-波长”，其中模型C9-60-480为基准模型，如表1所示．模型框架梁截面统一为H900mm×600mm×24mm×48mm，框架柱截面统一为H600mm×600mm×24mm×48mm，两侧加劲肋截面统一为300mm×30mm．

框架梁两侧对称布置8根预应力筋，每根预应力筋由公称直径为21.6mm、抗拉强度标准值为1860MPa的7股钢绞线捻制而成，截面积为285mm2．初始预应力取预应力筋极限承载力的30%[11]，为159kN．框架梁柱钢材为弹性模型，弹性模量为2.06×105MPa，泊松比为0.3；预应力筋钢材为弹性模型，弹性模量为1.96×105MPa，泊松比为0.3，热膨胀系数为1.2×10-5/℃；波纹墙板与加劲肋钢材为理想弹塑性模型，弹性模量为2.06×105MPa，泊松比为0.3，屈服强度为235MPa．

表1 模型参数设置

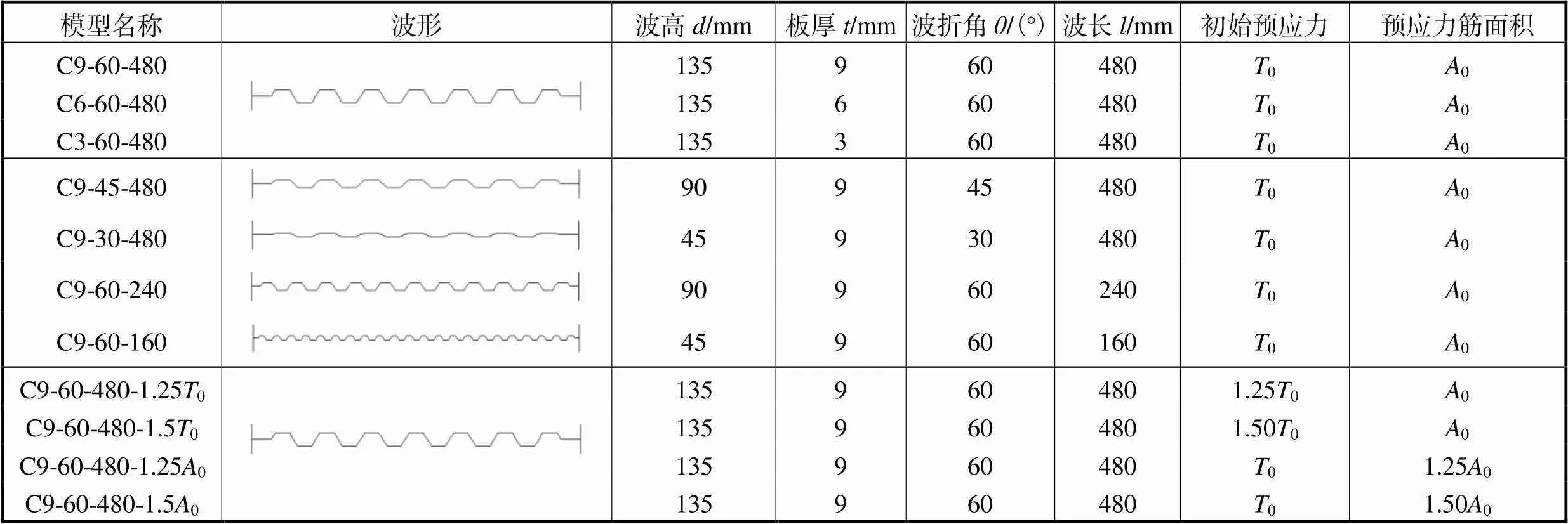
Tab.1 Analysis model parameters

注：0为初始预应力；0为预应力筋面积．

2.2 有限元模型的建立

有限元模型中采用梁单元B31模拟边框梁柱，壳单元S4R模拟波纹墙板及加劲肋．为简化分析，采用位于框架梁轴线上的桁架单元T3D2模拟预应力筋[6]，并通过降温237℃使其达到所需初始预应力．采用“tie”约束模拟墙板及侧边加劲肋与边框梁的焊接连接，一侧边框柱底约束2个方向的平动以模拟可动铰支座，一侧边框柱底约束3个方向的平动以模拟固定铰支座，模型示意如图4所示．

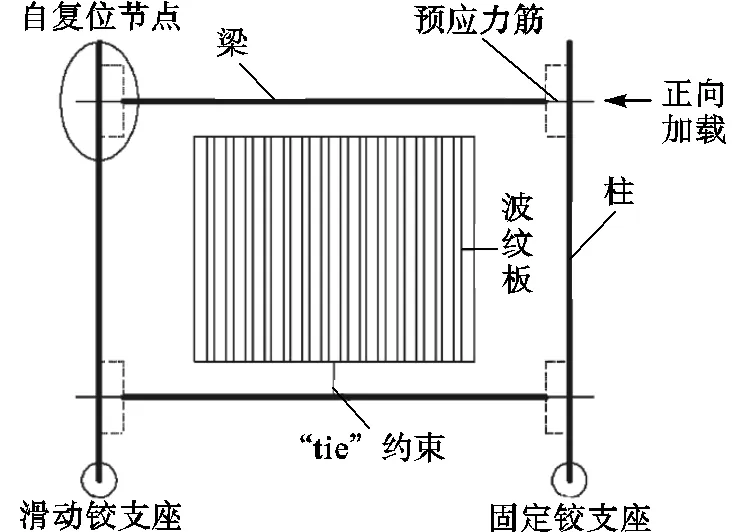
图4 有限元模型示意

自复位框架的梁柱节点设置如图5所示，首先在柱中轴线上对应于梁上、下翼缘及梁中轴线处分别创建3个主节点，在柱内侧翼缘上相同高度处创建3个从节点，主、从节点之间采用多点约束连接，以模拟柱节点域的刚性变形．在梁端中轴线及对应上、下翼缘处分别创建1个主节点和2个从节点，主、从节点之间采用多点约束连接，以将梁端部截面简化模拟为刚性平面．在梁端部3个节点及对应柱内侧翼缘上3个节点间分别采用连接单元axial connector及slot connector，其中axial设置受压刚度极大而受拉刚度为0，以模拟梁柱节点的张开与闭合，并传递梁柱之间的剪力．在梁中轴线上柱外侧翼缘处创建1个主节点，柱外侧翼缘上创建1个从节点，主、从节点之间采用“tie”约束，以模拟预应力筋端部的锚固．

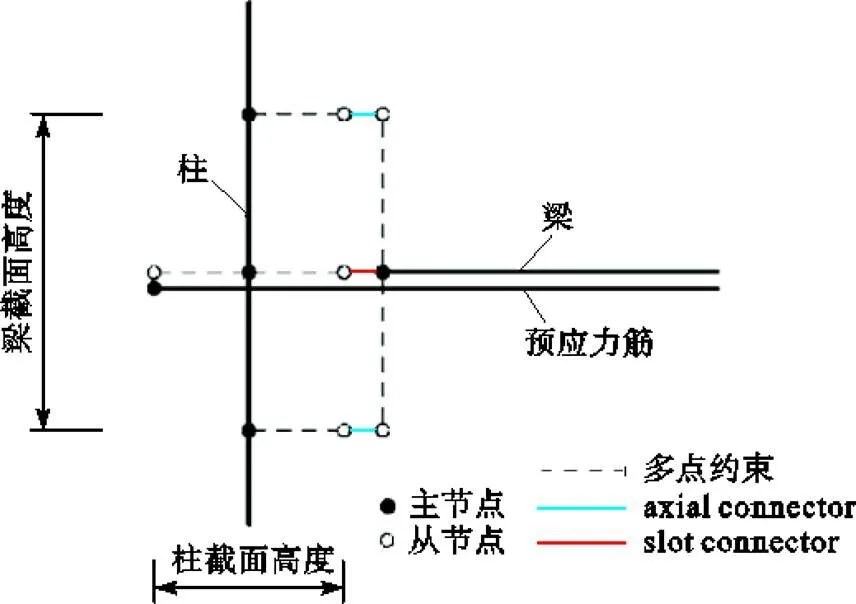
图5 自复位节点设置

滞回分析全程采用位移控制，并在对应梁中轴线的右柱主节点处进行加载，加载制度参考文献[11]，各级峰值层间侧移角分别为0.10%、0.25%、0.50%、1.00%、1.50%、2.00%、2.50%、3.00%、4.00%，且每级循环2圈．由于波纹板屈服后的变形较为复杂，计算不易收敛，采用动力显式算法进行滞回分析．

2.3 有限元模型验证

采用第2.2节的建模方法对文献[8]中的自复位平钢板剪力墙试件8s100k20Ga和6s75k20Ga进行滞回分析，试件为两层单跨SC-SPSW，一侧柱底采用滑动铰支座，另一侧柱底采用转动铰支座，试验加载装置如图6所示．

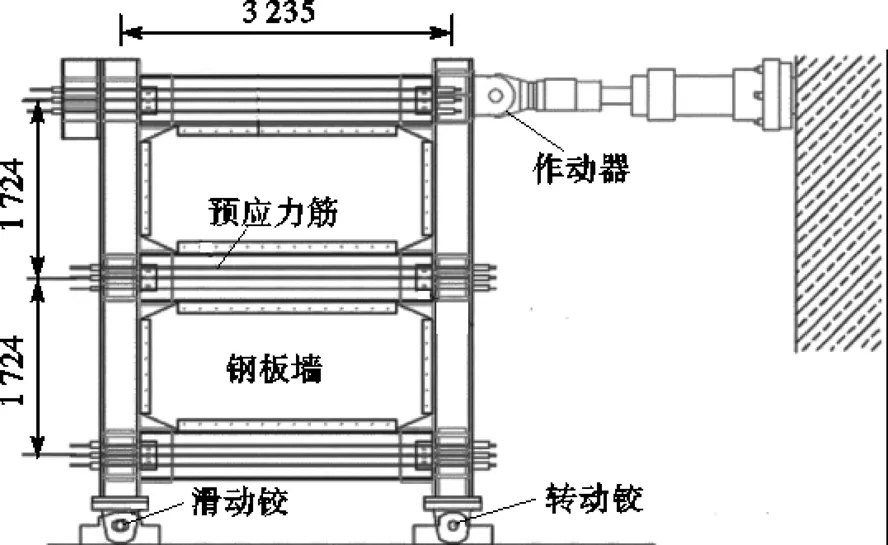
图6 文献[8]试验加载装置(单位：mm)

梁、柱截面尺寸分别为美国型钢W18×106和W14×132，采用钢材ASTM A992，弹性模量为203GPa．钢绞线采用ASTM A416，弹性模量为196.5GPa，每个PT节点中布置8 束，每束截面面积为98.7mm2．钢板墙采用ASTM A1008，厚度为0.92mm，其弹性模量、屈服强度和抗拉强度分别为172GPa、182MPa和325MPa．试验采用位移加载，各级峰值层间侧移角分别为0.088%、0.175%、0.263%、0.350%、0.700%、1.050%、1.400%、1.750%、2.100%、2.500%、3.000%、3.500%和4.000%，其中1.050%层间侧移角之前每级循环3圈，1.050%层间侧移角之后每级循环2圈．

有限元与试验滞回曲线的对比如图7所示，有限元与试验的变形对比如图8所示．由图7和图8可知，有限元分析结果与试验结果吻合良好，钢墙板在2.000%侧移角时有明显的面外屈曲变形并沿斜向拉力带进入屈服，上述建模方法可以较好地模拟自复位钢板剪力墙的滞回性能．

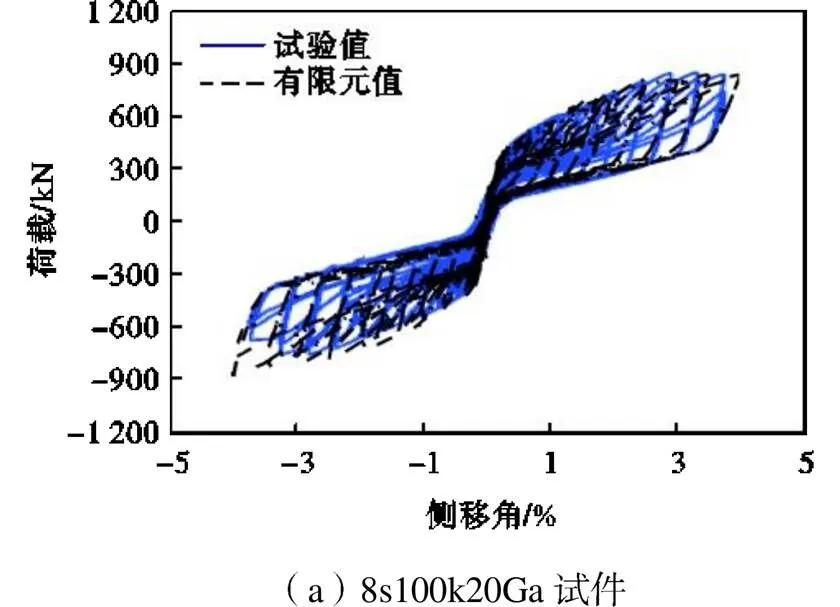
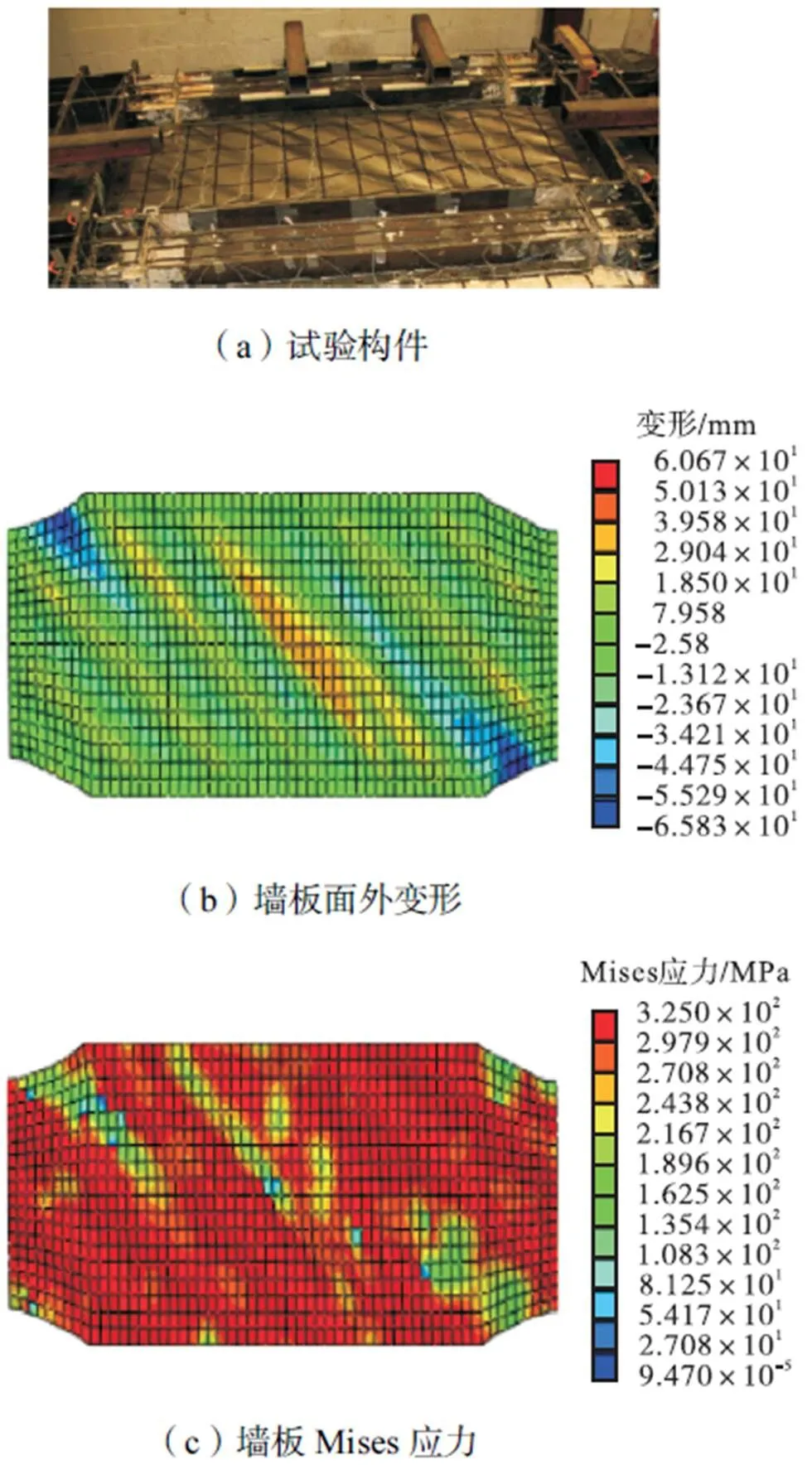
图8 2.000%侧移角时钢板墙变形对比

3 滞回性能及参数分析

3.1 墙板连接形式的影响

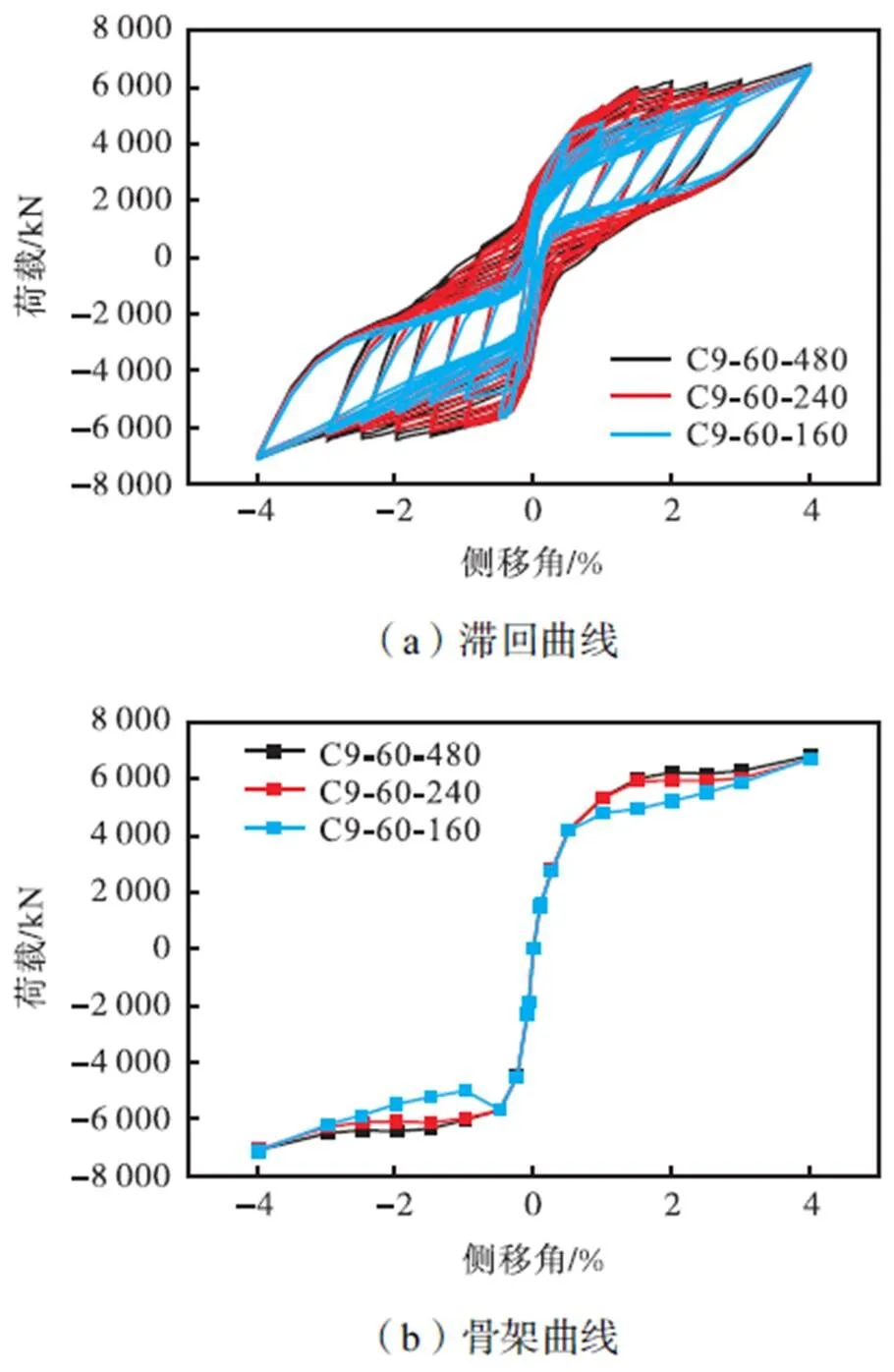
自复位两边连接和四边连接波纹钢板剪力墙模型的滞回曲线、骨架曲线、累积滞回耗能能力和残余侧移角随侧移角的变化曲线如图9所示．除墙板连接形式外，墙板厚度统一为9mm，墙板波折角统一为60°，波长统一为480mm，且自复位钢框架的构件截面与预应力水平不变．

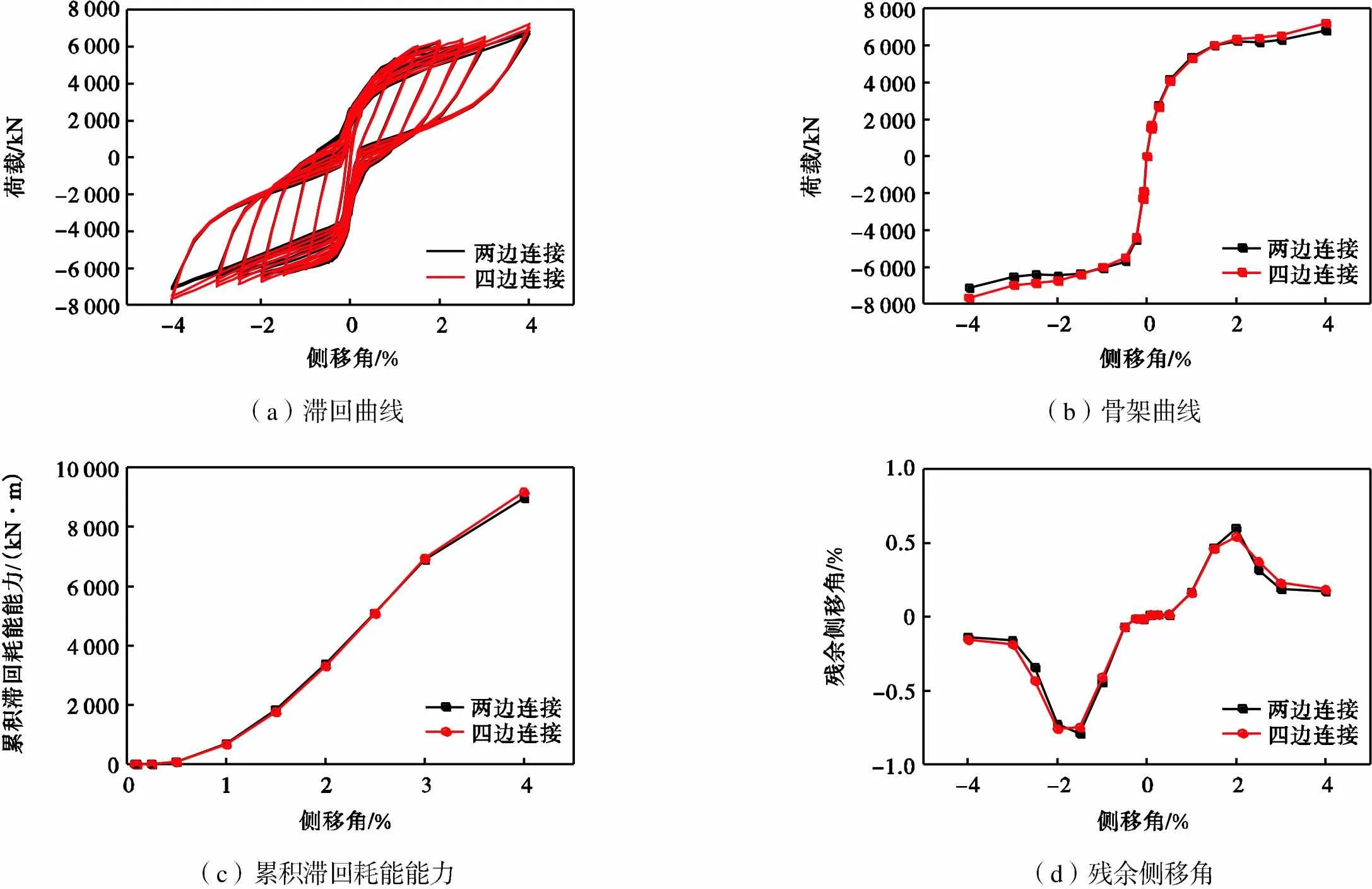
（a）滞回曲线（b）骨架曲线 （c）累积滞回耗能能力（d）残余侧移角

由图9可知，自复位两边连接和四边连接波纹钢板剪力墙的滞回曲线非常接近，均为双旗帜形．在侧移角小于0.5%时，墙板及边框处于弹性状态，耗能及残余侧移角均近似于0；随着侧移角的增加，墙板逐渐进入塑性，结构耗能及残余侧移角均迅速增加，但残余侧移角在侧移角为2%左右达到峰值，其后开始下降．相比四边连接，自复位两边连接波纹钢板剪力墙在2%侧移角时承载力与耗能能力几乎相同，残余侧移增加0.06%，在4%侧移角时承载力与耗能能力低10%左右，而残余侧移角几乎相同．

值得指出的是，自复位两边连接及四边连接波纹钢板剪力墙的板厚及波形尺寸完全相同，并且由于四边连接波纹钢板剪力墙采用了角部切角的措施，其波纹边与框架梁的锚固长度亦相同．在竖向波纹墙板以剪切方式承载的情况下，侧向承载力主要取决于波纹边锚固长度，因此，四边连接与两边连接的结构承载力几乎一样，如图9所示．图10和图11显示了两边连接和四边连接波纹墙板在发生剪切屈服时(0.5%侧移角)的应力云图与面外变形．由图10和图11可知，波纹板以面内剪切的方式承载，两边连接波纹钢板剪力墙全板达到剪切屈服．角部切角的四边连接波纹钢板剪力墙由于切角处发生面外屈曲，角部切角范围内应力较小，而波纹边锚固长度范围内的墙板只在中间区域达到屈服应力，并没有发生全部剪切屈服．因此，自复位两边连接和四边连接波纹钢板剪力墙的有效剪切面积近似相同，滞回曲线、承载力和耗能能力均较接近．

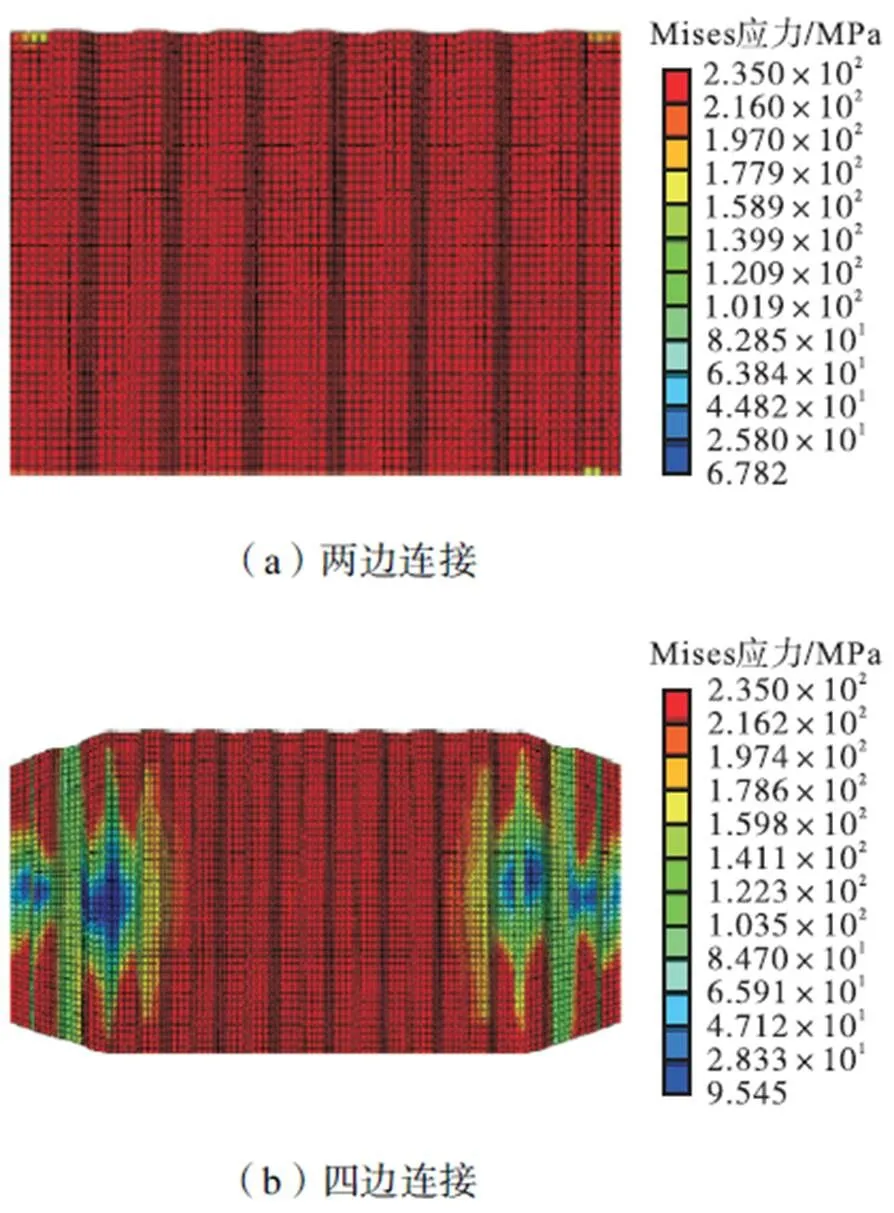
图10 波纹墙板在0.5%侧移角时的Mises应力对比

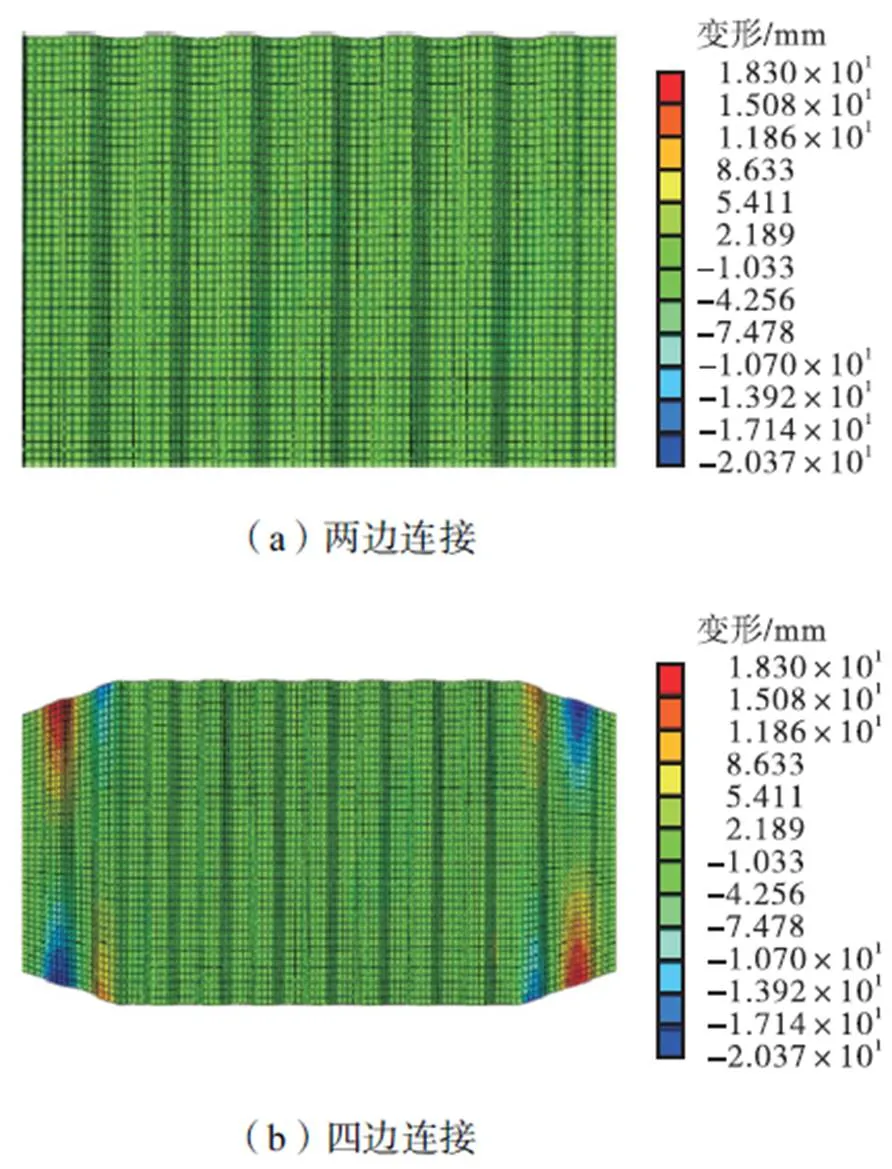
图11 波纹墙板在0.5%侧移角时的面外变形对比

3.2 波纹墙板几何尺寸的影响

3.2.1 波纹墙板厚

不同厚度的自复位两边连接波纹钢板剪力墙的滞回曲线、骨架曲线、单位板厚的累积耗能能力和残余侧移角随侧移角的变化曲线如图12所示．除墙板厚度外，墙板波折角统一为60°，波长统一为480mm，且自复位钢框架的构件截面与预应力水平不变．

由图12(a)、(b)可知，随着墙板厚度从3mm增加至9mm，自复位两边连接波纹钢板剪力墙的滞回曲线越加饱满，前期承载力显著提高，在2%和4%侧移角下增幅分别高达40%和20%．由图12(c)可知，侧移角超过0.5%后，单位板厚的结构累积耗能随侧移的增加而增加，且随着墙板厚度的增加急剧上升，4%侧移角下增幅高达50%．但值得注意的是，结构残余侧移角随侧移角的增加而增加，且随着墙板厚度的增加亦急剧上升，当板厚为9mm时2%侧移角下的残余侧移角超出结构可修限值0.5%[8]．这主要是由于墙板厚度为3mm及6mm时，墙板在0.25%～0.50%侧移时发生弹塑性屈曲，如图13(a)、图14(a)所示，墙板受压承载力由于屈曲显著降低，因此残余受压承载力及残余侧移角较低．墙板屈曲时，自复位钢框架的预应力筋随侧移角的增加而伸长，承载力逐渐增加，因而整体结构的承载力没有因墙板屈曲而降低．墙板厚度为9mm时，墙板在0.5%侧移角时发生剪切屈服，如图13(b)、图14(b)所示，拉压承载力较为对称，因此残余受压承载力及残余侧移角较高，并在2%侧移角时达到峰值，其后墙板由于过大的面外变形使得残余受压承载力及残余侧移角逐渐下降．

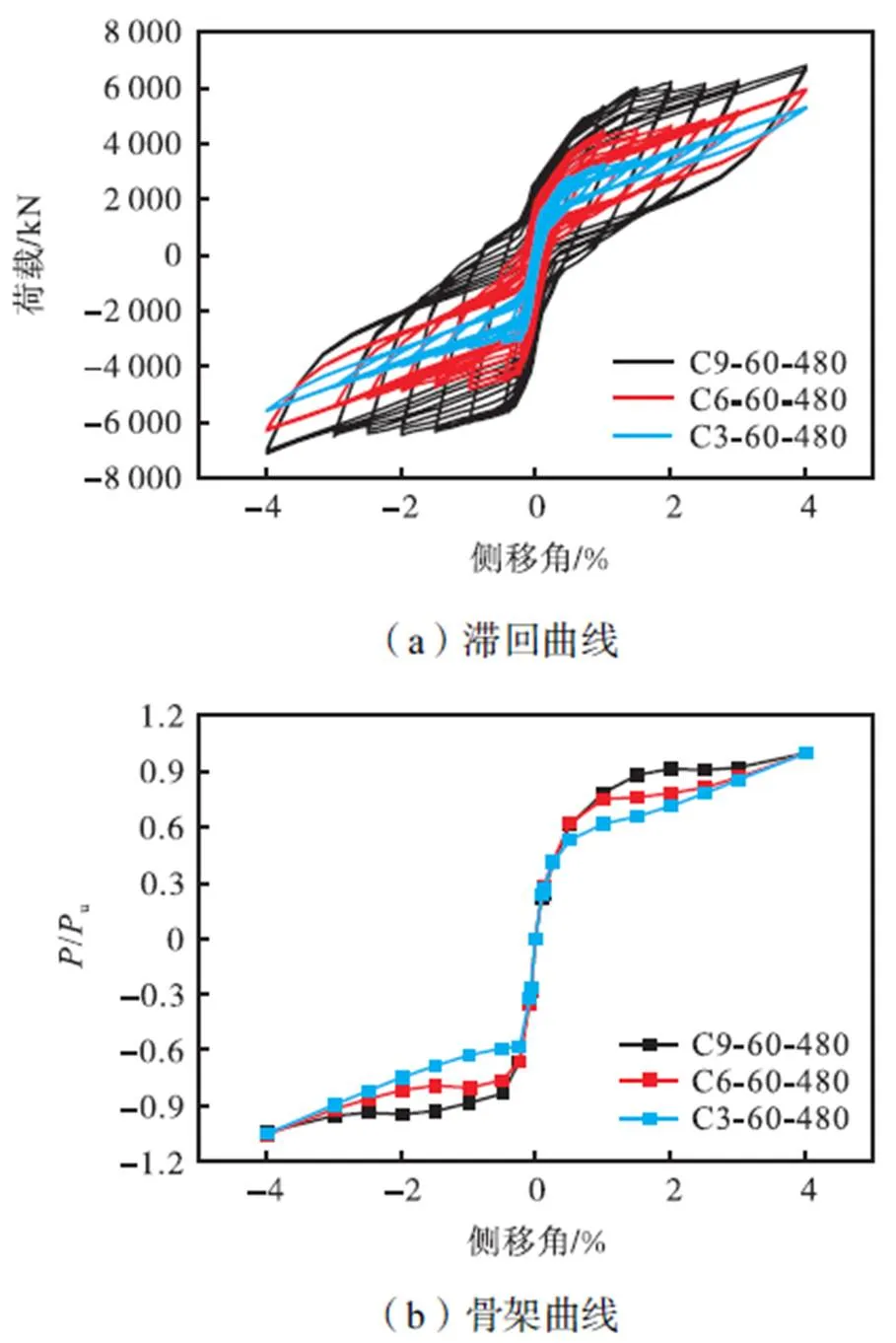
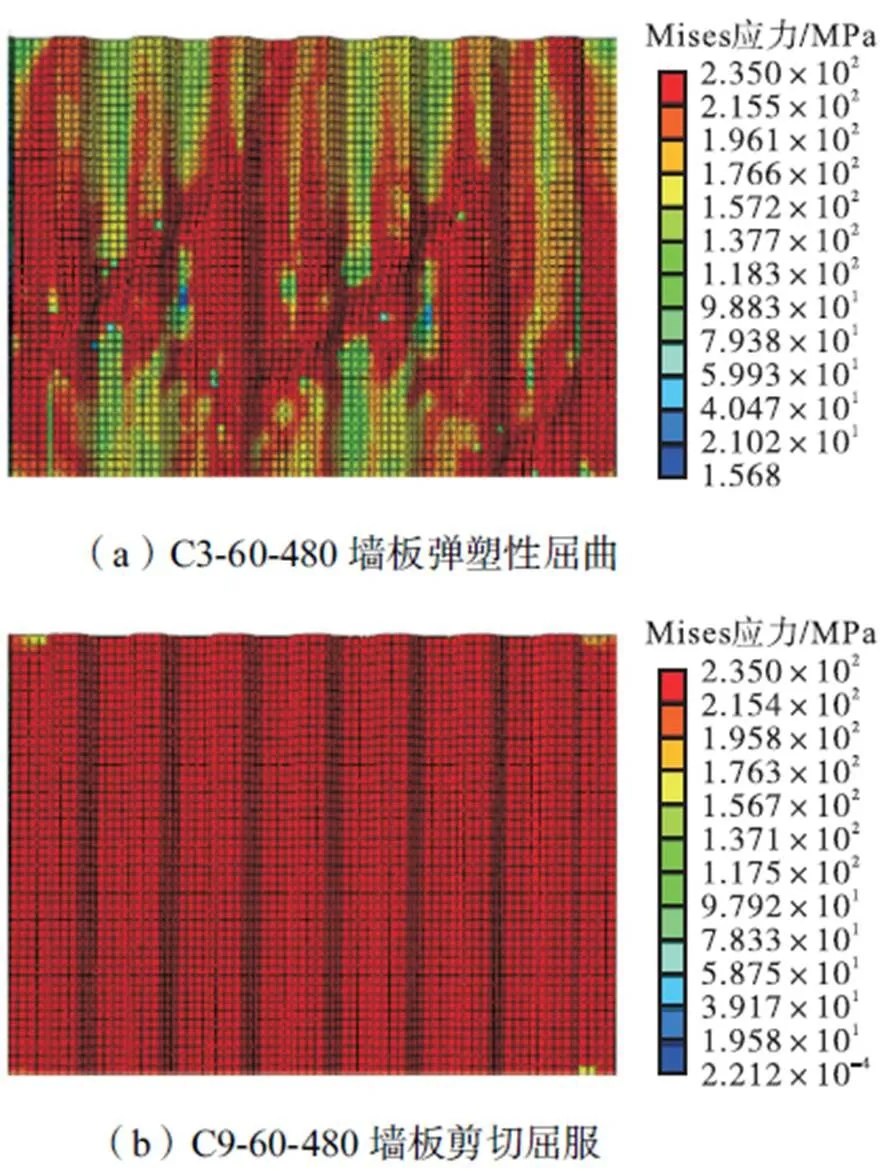
图13 波纹墙板在0.5%侧移角时的Mises应力对比

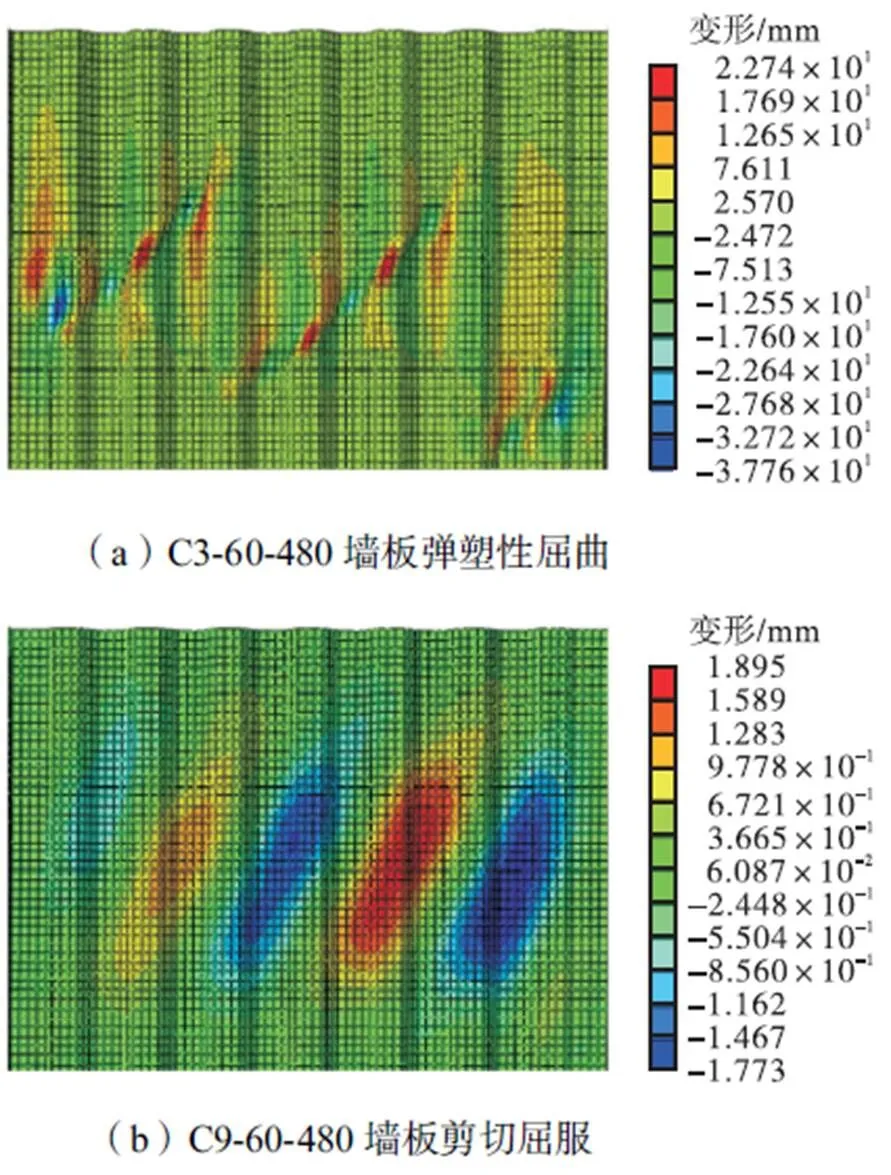
图14 波纹墙板在0.5%侧移角时的面外变形对比

3.2.2 波纹墙板波折角

不同波折角的自复位两边连接波纹钢板剪力墙的滞回曲线、骨架曲线、累积滞回耗能能力和残余侧移角随侧移角的变化曲线如图15所示．除波折角变化外，墙板厚度统一为9mm，波长统一为480mm，且自复位钢框架的构件截面与预应力水平不变．

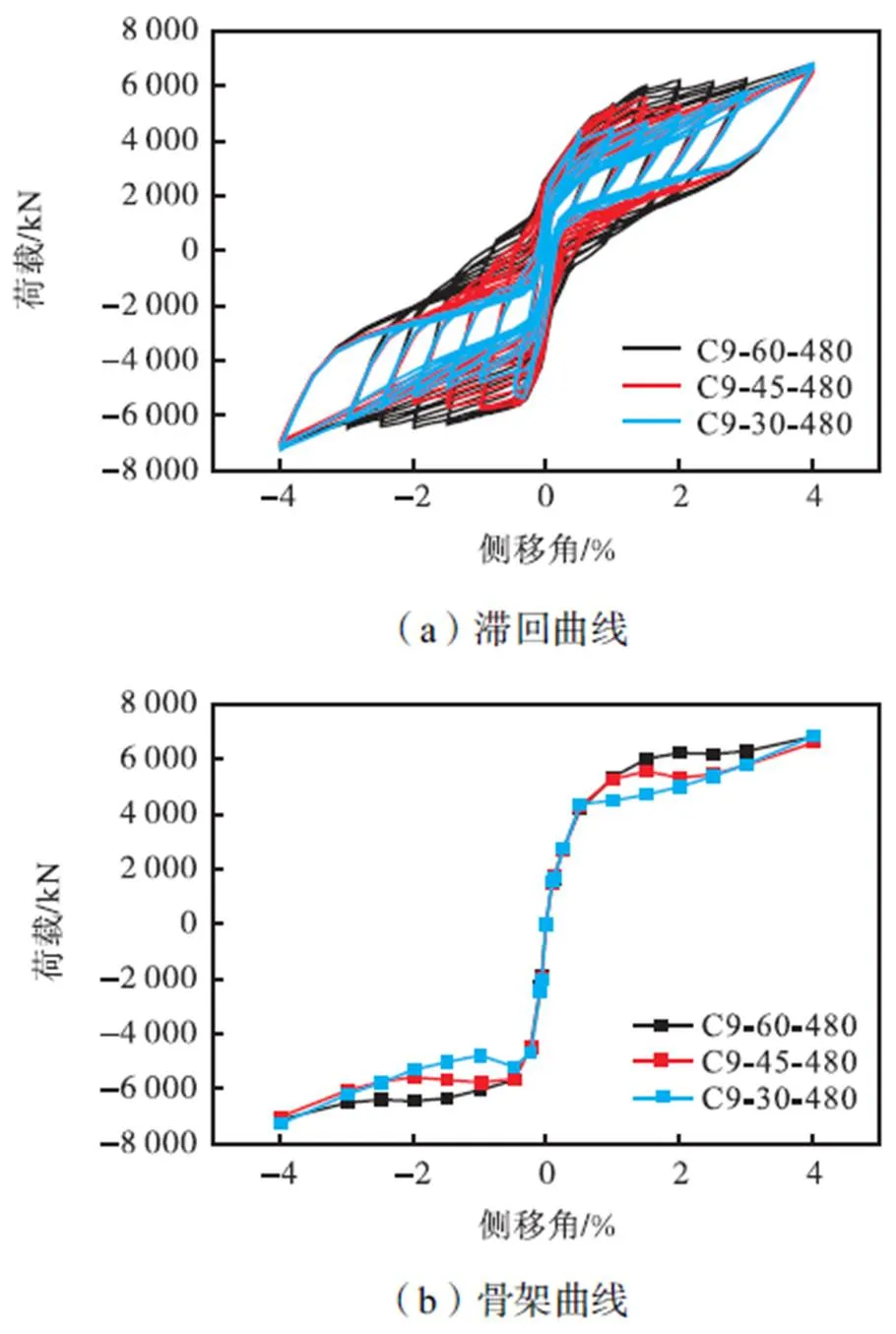
由图15(a)、(b)可知，随着墙板波折角从30°增加至60°，自复位两边连接波纹钢板剪力墙的滞回曲线越加饱满，且捏缩更不明显．承载力在2%侧移角之前可提高30%，2%侧移角之后逐渐接近．这是由于波折角为30°的墙板在0.5%侧移角时发生弹塑性屈曲，其后墙板承载力下降，如图16所示．而波折角为45°及60°的墙板在0.5%侧移角时大部分墙板达到剪切屈服，其后墙板承载力保持稳定，因此结构承载力随波折角的增加而增加．在2%侧移角之后，墙板波纹随着侧移角的增加逐渐展开，部分形成拉力带承载，因此剪力墙的承载力差异变小．

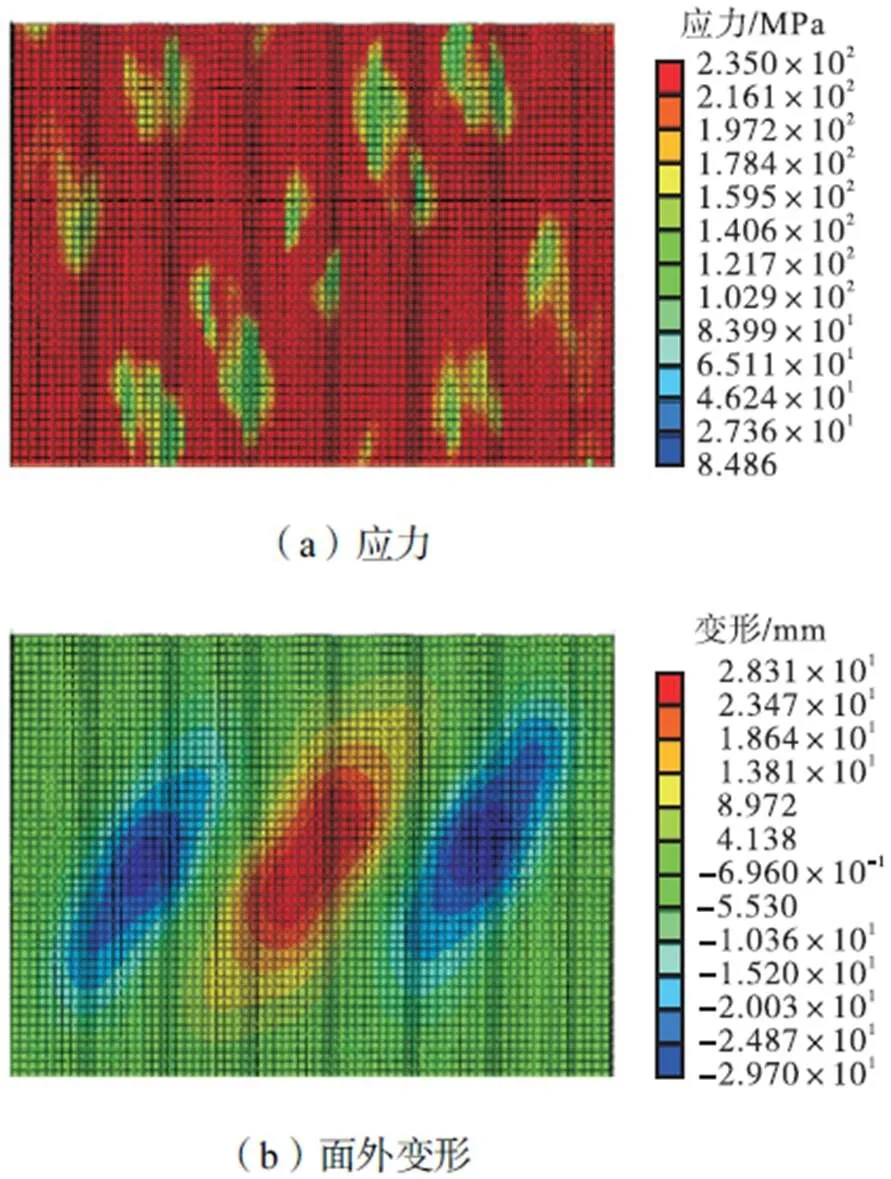
图16 C9-30-480墙板在0.5%侧移角时发生的弹塑性屈曲

由图15(c)可知，侧移角超过0.5%后，结构耗能随着墙板波折角的增加而增加，4%侧移角下增幅高达60%．由图15(d)可知，结构残余侧移角随侧移角的增加而增加，且墙板波折角为60°时残余侧移角显著高于波折角为30°及45°时，2%侧移角下的残余侧移角超出结构可修限值0.5%[8]，值得注意．这是由于前两类墙板剪切屈服后拉压承载力较为对称，导致残余受压承载力及残余侧移角较高，并在2%侧移角时达到峰值，其后墙板由于过大的面外变形使得残余受压承载力及残余侧移角逐渐下降，而波折角为30°的墙板弹塑性屈曲后，残余受压承载力及残余侧移角始终较低．

3.2.3 波纹墙板波长

不同波长的自复位两边连接波纹钢板剪力墙的滞回曲线、骨架曲线、累积滞回耗能能力和残余侧移角随侧移角的变化曲线如图17所示．除墙板波长外，墙板厚度统一为9mm，波折角统一为60°，且自复位钢框架的构件截面与预应力水平不变．

由图17(a)、(b)可知，随着墙板波长从160mm增加至480mm，自复位两边连接波纹钢板剪力墙的滞回曲线越加饱满，且捏缩更不明显．墙板波长为480mm和240mm的承载力较为接近，在2%侧移角前相比墙板波长为160mm的承载力发挥效率可提高16%，2%侧移角之后三者承载力逐渐趋同．这主要是由于墙板的波高及剪切屈曲承载力随波长的增加而增加，结构承载力亦随之提高，而2%侧移角之后随着波纹的展开，结构承载力差异变小．由图17(c)可知，侧移角超过0.5%后，结构耗能随着墙板波折角的增加而增加，其中波长为480mm的模型与波长为240mm的模型耗能能力相近，相比于波长为160mm的模型，耗能能力可以提高50%．由图17(d)可知，结构残余侧移角亦随着墙板波长的增加而增加，且墙板波长为240mm及480mm的残余侧移角显著高于波长为160mm，2%侧移角下的残余侧移角均超出结构可修限值0.5%[8]，值得注意．这是由于波长为480mm和240mm的波纹板在0.5%侧移角时发生剪切屈服，拉压承载力较为对称，导致残余受压承载力及残余侧移角较高，在2%侧移角时达到峰值，而波长为160mm的波纹板在0.5%侧移角时发生弹塑性屈曲，如图18所示，残余侧移角始终较小．

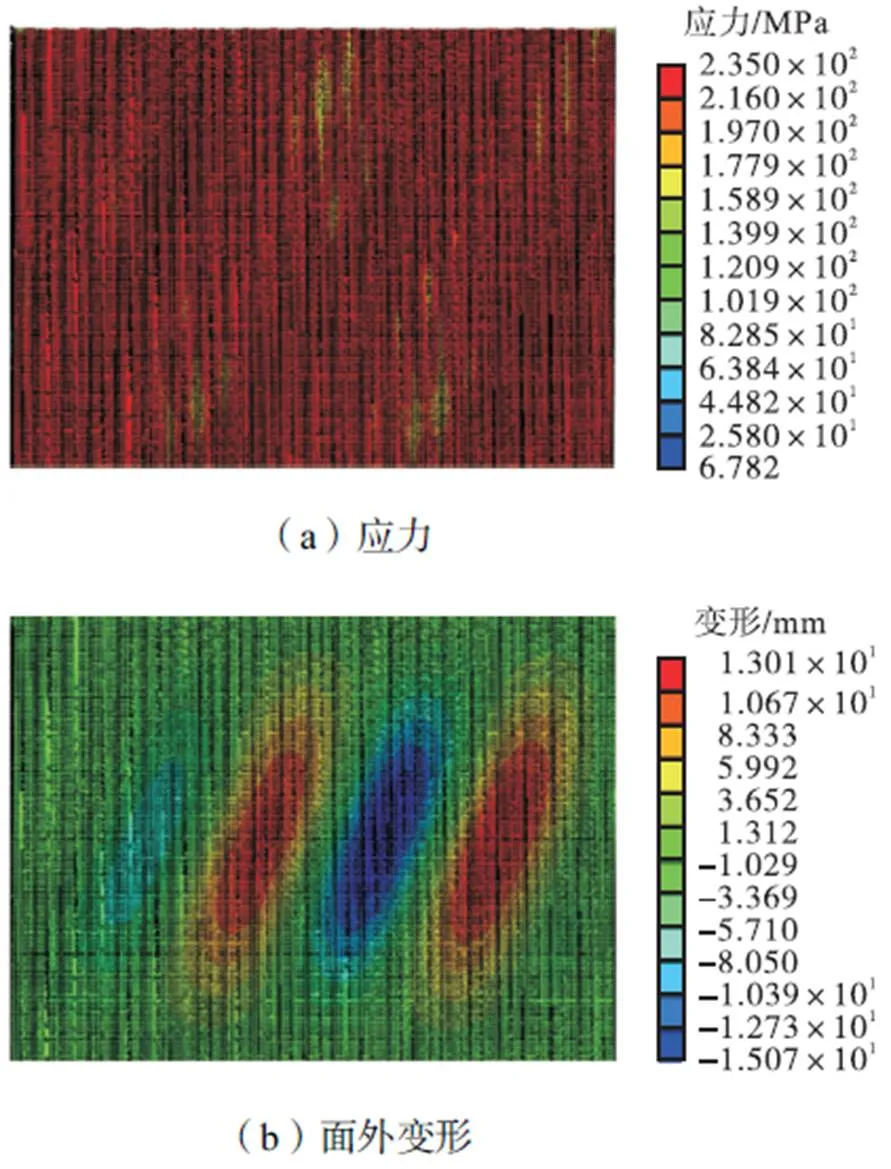
图18 C9-60-160墙板在0.5%侧移角时发生的弹塑性屈曲

综上，增加墙板厚度、波折角和波长可以有效提高结构的承载力发挥效率和耗能能力，减小捏缩效应，但可能引起残余侧移角的显著增大，设计时应综合考虑耗能性能和复位性能之间的平衡．

3.3 预应力筋参数的影响

3.3.1 初始预应力

不同初始预应力的自复位两边连接波纹钢板剪力墙的滞回曲线、骨架曲线、累积滞回耗能能力和残余侧移角随侧移角的变化曲线如图19所示．除初始预应力外，预应力筋面积统一为285mm2，墙板厚度统一为9mm，波折角统一为60°，波长统一为480mm，且框架构件截面不变．

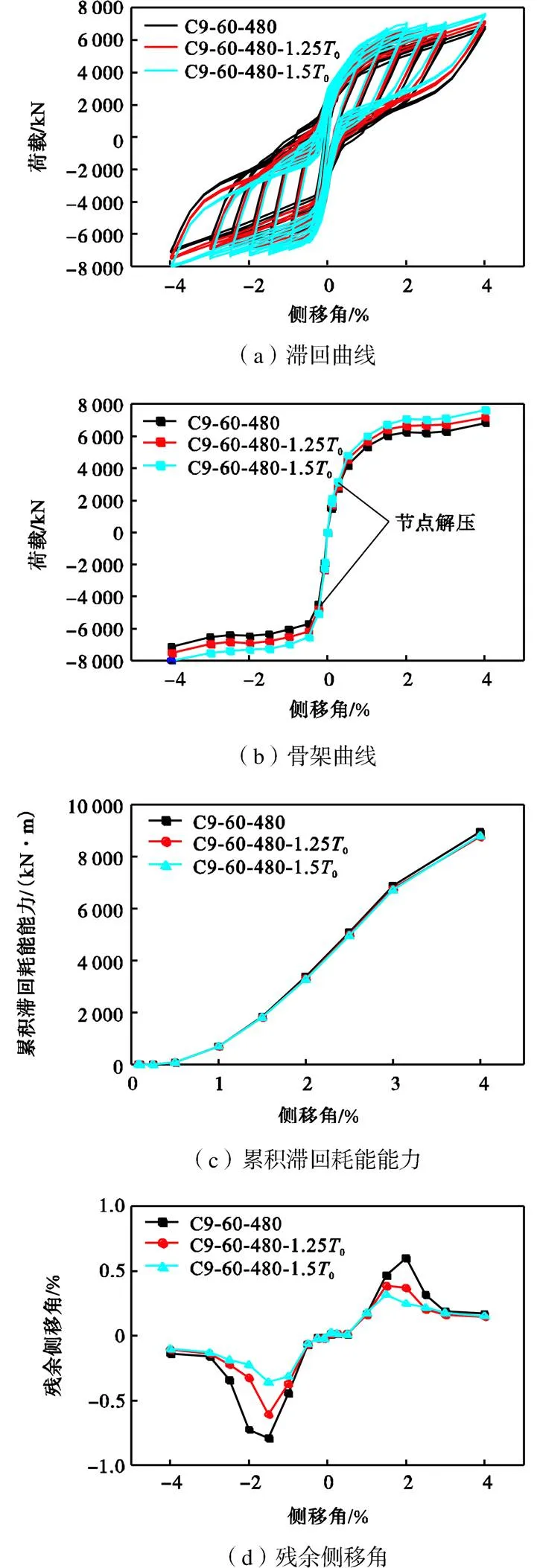
图19 不同初始预应力的自复位波纹钢板剪力墙的性能曲线

由图19(a)、(b)可知，侧移角为0.25%时自复位两边连接波纹钢板剪力墙的边框梁柱节点解压．节点解压前，结构初始抗侧刚度基本相同；节点解压后，结构承载力随初始预应力的增加而增加，初始预应力增加50%后承载力可提高13%，而抗侧刚度基本不变，滞回曲线的捏缩更加明显．由图19(c)、(d)可知，初始预应力对结构耗能能力的影响较小，但残余侧移角随初始预应力的增加显著减小．初始预应力增加50%后，2%侧移角下结构残余侧移角从0.80%降至0.35%，满足了结构可修限值的要求[8]．

3.3.2 预应力筋面积

不同预应力筋面积的自复位两边连接波纹钢板剪力墙的滞回曲线、骨架曲线、累积滞回耗能能力和残余侧移角随侧移角的变化曲线如图20所示．除预应力筋面积外，初始预应力统一为159kN，墙板厚度统一为9mm，波折角统一为60°，波长统一为480mm，且框架构件截面不变．

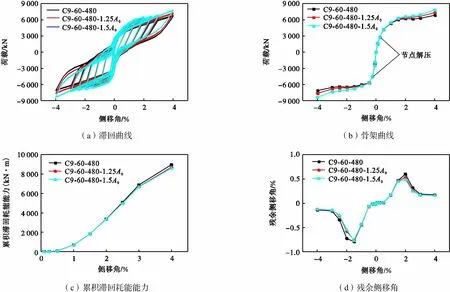
（a）滞回曲线（b）骨架曲线 （c）累积滞回耗能能力（d）残余侧移角

由图20(a)、(b)可知，侧移角为0.25%时自复位两边连接波纹钢板剪力墙的边框梁柱节点解压．由于自复位框架解压前的抗侧承载力仅与初始预应力相关，节点解压前，自复位两边连接波纹钢板剪力墙结构的抗侧承载力完全相同；节点解压后，结构抗侧承载力随预应力筋面积的增加而增加，预应力筋面积增加50%后，抗侧承载力提高15%，而滞回曲线的捏缩更加明显．由图20(c)、(d)可知，预应力筋面积对结构耗能能力及残余侧移角的影响均较小．预应力筋面积增加50%后，2%侧移角下结构正向残余侧移角虽从0.60%减小到0.48%，但负向残余侧移角仍可达0.7%，超出结构可修限值0.5%[8]，值得注意．

综上，增加预应力筋的初始预应力可提高节点解压后结构的承载力并显著降低残余侧移角，对结构耗能能力影响较小；增加预应力筋面积可提高节点解压后结构的承载力，但对结构耗能能力及残余侧移角的影响均较小．

4 结论

本文提出一种自复位两边连接梯形波纹钢板剪力墙结构，通过ABAQUS建立了结构的有限元模型并进行非线性滞回分析，以研究墙板连接形式、波形参数及预应力水平对结构滞回性能和复位性能的影响．主要结论如下．

(1) 相比于角部切角的自复位四边连接波纹钢板剪力墙，自复位两边连接梯形波纹钢板剪力墙的承载力、耗能能力及残余侧移角基本相同，且可避免墙角过早撕裂及灵活布置门窗洞口．自复位两边连接梯形波纹钢板剪力墙的最大残余侧移角基本出现在2%侧移角时，之后显著降低，4%侧移角时基本在0.2%之内．

(2) 随着波纹墙板厚度由3mm增大到9mm，自复位两边连接波纹钢板剪力墙结构的承载力发挥效率和耗能能力分别提高40%和80%，但最大残余侧移角由0.10%激增至0.75%，超过结构可修限值0.5%，值得注意．

(3) 随着波纹墙板波折角由60°减小到30°，自复位两边连接波纹钢板剪力墙结构的最大残余侧移角可降到0.15%，但2%侧移角下的承载力发挥效率降低30%，4%侧移角下承载力基本不变，耗能能力降低60%．

(4) 随着波纹墙板波长由480mm减小到160mm，自复位两边连接波纹钢板剪力墙结构的最大残余侧移角可降到0.2%，但2%侧移角下的承载力发挥效率降低16%，4%侧移角下承载力基本不变，耗能能力降低50%．

(5) 预应力筋初始预应力增加50%后，自复位两边连接波纹钢板剪力墙结构的承载力提高13%，最大残余侧移角可由0.80%降到0.35%，耗能能力基本不变．预应力筋面积增加50%后，自复位两边连接波纹钢板剪力墙结构的承载力提高15%，但对结构耗能能力及残余侧移角的影响均较小．

(6) 采用剪切屈服控制的波纹墙板时，自复位两边连接波纹钢板剪力墙结构的承载力和耗能能力较高，但最大残余侧移亦较大，可通过提高预应力筋初始预应力加以控制．采用弹塑性屈曲控制的波纹墙板时，自复位两边连接波纹钢板剪力墙结构的最大残余侧移角较小，承载力略低于墙板剪切屈服的结构，但耗能能力明显降低．因此，需综合考虑及选择波纹墙板的几何参数与预应力水平，使自复位两边连接波纹钢板剪力墙充分发挥承载力和耗能能力，并有效控制震后残余侧移角．

［1］ Timler P A，Kulak G L. Experimental study of steel plate shear walls[J]. Minnesota Medicine，1983，69(5)：268-270.

［2］ 郭彦林，董全利. 钢板剪力墙的发展与研究现状[J]. 钢结构，2005，20(1)：1-6.

Guo Yanlin，Dong Quanli. Research and application of steel plate shear wall in high-rise buildings[J]. Steel Construction，2005，20(1)：1-6(in Chinese).

［3］ 郭兰慧，李 然，张素梅. 薄钢板剪力墙简化分析模型[J]. 工程力学，2013，30(6)：149-153.

Guo Lanhui，Li Ran，Zhang Sumei. Simplified model of thin-walled steel plate shear walls[J]. Engineering Mechanics，2013，30(6)：149-153(in Chinese).

［4］ Berman J W，Clayton P M，Lowes L N，et al. Development of a recentering steel plate shear wall and addressing critical steel plate shear wall research needs[C]//Proceedings of the 9th US National Conference on Earthquake Engineering. Toronto，Canada，2010：1087.

［5］ Clayton P M，Berman J W，Lowes L N. Seismic design and performance of self-centering steel plate shear walls[J]. Journal of Structural Engineering，2012，138(1)：22-30.

［6］ Clayton P M. Self-Centering Steel Plate Shear Walls：Development of Design Procedure and Evaluation of Seismic Performance[D]. Seattle： Department of Civil and Environmental Engineering，University of Washington，2010.

［7］ Winkley T B. Self-Centering Steel Plate Shear Walls：Large Scale Experimental Investigation[D]. Seattle：Department of Civil and Environmental Engineering，University of Washington，2011.

［8］ Clayton P M，Winkley T B，Berman J W，et al. Experimental investigation of self-centering steel plate shear walls[J]. Journal of Structural Engineering(ASCE)，2012，138(7)：952-960.

［9］ Clayton P M，Berman J W，Lowes L N. Seismic performance of self-centering steel plate shear walls with beam-only-connected web plates[J]. Journal of Constructional Steel Research，2015，106：198-208.

［10］ Clayton P M，Berman J W，Lowes L N. Mitigating web plate damage and reducing frame demands in resilient steel plate shear walls[C]//Structures Congress 2015. USA，2015：2421-2432.

［11］ Clayton P M，Berman J W，Lowes L N. Subassembly testing and modeling of self-centering steel plate shear walls[J]. Engineering Structures，2013，56(6)：1848-1857.

［12］ 徐基磊，李启才，经 聪，等. 利用带缝钢板剪力墙耗能的自复位体系研究[J]. 苏州科技学院学报(工程技术版)，2014，27(3)：27-33.

Xu Jilei，Li Qicai，Jing Cong，et al. Research on the self-centering system using energy dissipation of the steel plate shear wall with seams[J]. Journal of Suzhou University of Science and Technology(Engineering Technology Edition)，2014，27(3)：27-33(in Chinese).

［13］ Lu J，Zhang H，Yu S. Study on seismic behaviors of self-centering steel plate shear walls with slits[J]. Journal of Constructional Steel Research，2021，185(10)：106878.

［14］ Wang W，Kong J，Zhang Y，et al. Seismic behavior of self-centering modular panel with slit steel plate shear walls：Experimental testing[J]. Journal of Structural Engineering，2018，144(1)：04017179.

［15］ 周林丽. 自复位半圆形波纹钢板剪力墙体系抗震性能研究[D]. 广州：广州大学，2020.

Zhou Linli. Study on Seismic Performance of Self-Resetting Semicircular Corrugated Steel Plate Shear Wall System[D]. Guangzhou：Guangzhou University，2020(in Chinese).

［16］ 谭 平，周林丽，滕晓飞. 自复位钢框架-半圆形波纹钢板剪力墙滞回性能研究[J]. 建筑结构学报，2021，42(3)：185-192.

Tan Ping，Zhou Linli，Teng Xiaofei. Research on hysteretic performance of self-resetting steel frame-semi-circular corrugated steel plate shear wall[J]. Journal of Building Structures，2021，42(3)：185-192(in Chinese).

［17］ GB 50011—2010 建筑抗震设计规范[S]. 北京：中国建筑工业出版社，2010.

GB 50011—2010 Code for Seismic Design of Buildings [S]. Beijing：China Building Industry Press，2010(in Chinese).

［18］ 赵 煜. 波纹钢板剪力墙结构基于性能的抗震设计方法研究[D]. 天津：天津大学，2018.

Zhao Yu. Research on Performance-Based Seismic Design Method of Corrugated Steel Plate Shear Wall Structure[D]. Tianjin：Tianjin University，2018(in Chinese).

［19］ 赵秋红，邱 静，郝博超，等. 两边连接竖向波纹钢板剪力墙的抗侧性能[J]. 天津大学学报(自然科学与工程技术版)，2019，52(增2)：46-53.

Zhao Qiuhong，Qiu Jing，Hao Bochao，et al. Lateral performance of shear walls with vertical corrugated steel plates connected on both sides[J]. Journal of Tianjin University(Science and Technology)，2019，52(Suppl 2)：46-53(in Chinese).

［20］ Tong G，Sause R. Analysis of local elastic shear buckling of trapezoidal corrugated steel webs[J]. Journal of Constructional Steel Research，2014，102：59-71.

［21］ Berman J W，Bruneau M. Experimental investigation of light-gauge steel plate shear walls[J]. Journal of Structural Engineering，2005，131(2)：259-267.

［22］ 金华建，孙飞飞，李国强. 无屈曲波纹钢板墙抗震性能与设计理论[J]. 建筑结构学报，2020，41(5)：53-64.

Jin Huajian，Sun Feifei，Li Guoqiang. Seismic performance and design theory of non-buckling corrugated steel plate wall[J]. Journal of Building Structures，2020，41(5)：53-64(in Chinese).

［23］ Qiu Jing，Zhao Qiuhong，Yu Cheng，et al. Experimental studies on cyclic behavior of corrugated steel plate shear walls[J]. Journal of Structural Engineering，2018，144(11)：04018200.

［24］ 赵秋红，李 楠，孙军浩. 波纹钢板剪力墙结构的抗侧性能分析[J]. 天津大学学报(自然科学与工程技术版)，2016，49(增1)：152-160.

Zhao Qiuhong，Li Nan，Sun Junhao. Lateral performance analysis of corrugated steel plate shear wall structure[J]. Journal of Tianjin University(Science and Technology)，2016，49(Suppl 1)：152-160(in Chinese).

［25］ Wang W，Ren Y，Lu Z，et al. Experimental study of the hysteretic behaviour of corrugated steel plate shear walls and steel plate reinforced concrete composite shear walls[J]. Journal of Constructional Steel Research，2019，160：136-152.

Hysteretic Behavior Analysis of Self-Centering Trapezoidal Corrugated Steel Plate Shear Wall with Beam-Only Connected Web Plates

Tan Zhilun1，Zhao Qiuhong1, 2

(1. School of Civil Engineering，Tianjin University，Tianjin 300350，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300350，China)

This paper proposes a self-centering trapezoidal corrugated steel plate shear wall structure with beam-only connected web plates，including a self-centering steel frame and embedded trapezoidal vertical corrugated steel wall panels. The wall panels are connected only to the beams to facilitate assembly construction. The general finite element software ABAQUS is used to establish a three-dimensional finite element model of a single-layer single-span self-centering trapezoidal corrugated steel plate shear wall and perform nonlinear hysteresis analysis to investigate the influence of wall panel connection form，wall panel waveform，and the prestress level of the structure on the hysteretic and recentering performances. The results show that the self-centering trapezoidal corrugated steel plate shear wall connected on beam only can effectively dissipate the seismic energy and control the residual drift after an earthquake. When the lateral side is stiffened，its bearing capacity，energy dissipation capacity，and residual drift are relatively equal with the self-centering corrugated steel plate shear wall with web plates in which a corner is cut out and connected with beam and column. With increasing thickness，the lateral resistance mode of the corrugated steel plate shear wall connected on beam only changes from shear buckling to shear yield，and the structural bearing capacity and energy dissipation capacity per unit thickness increase significantly. When the thickness increases from 3mm to 9mm，the amplitude is 40% and 50%，respectively. Notably，however，the residual drift of the structure also significantly increases to 0.5% above the repairable limit. With the reduction of the corrugation angle or wavelength of the corrugated wall panel，the residual drift of the structure can be effectively reduced. However，the bearing and energy consumption capacities of the structure are reduced，and the maximum drop can reach 30% and 60%，respectively. Alternatively，as the initial prestress of the post-tensioned tendons is increased by 50%，the structural bearing capacity increases by 13%，and the maximum residual drift significantly decreases from 0.80% to 0.35%，while the energy consumption capacity is unchanged. The bearing capacity of the structure increases with the area of the post-tensioned tendons，while the residual drift and energy dissipation capacity remain basically unchanged. Therefore，the buckling and lateral resistance modes of the beam-only connected corrugated steel wall panel have obvious effects on the hysteresis and self-centering behavior of self-centering corrugated steel plate shear wall，and the effects are not completely consistent with the traditional corrugated steel plate shear wall. The geometric parameters of the corrugated wall panels and the prestress level must be comprehensively considered and selected so that the self-centering corrugated steel plate shear wall connected on beam only can make full use of the bearing and energy consumption capacities and effectively control the residual drift after an earthquake.

self-centering trapezoidal corrugated steel plate shear wall；beam-only connections；hysteretic analysis；finite element parametric analysis；seismic behavior

10.11784/tdxbz202110010

TU391

A

0493-2137(2022)12-1262-13

2021-10-12；

2021-11-25.

谭志伦（1992—  ），男，博士研究生，zltan@tju.edu.cn.

赵秋红，qzhao@tju.edu.cn.

国家自然科学基金资助项目(51878447，51678406)；天津市研究生科研创新项目(2020YJSB084).

Supported by the National Natural Science Foundation of China(No. 51878447，No. 51678406)，Tianjin Postgraduate Research and Innovation Project(No. 2020YJSB084).

(责任编辑：金顺爱)