大载荷货梯曳引系统振动研究

周 晗， 王 亮， 李海超， 简学科， 魏义敏， 李剑敏*

(1.浙江理工大学 机械与自动控制学院， 浙江 杭州 310018；2.杭州奥立达电梯有限公司， 浙江 杭州 311619)

货梯是企业对物品进行垂直搬运的重要工具，随着社会与工业发展所需搬运的货物越来越重，货梯的载荷也不断增加。一般将载荷大于5 t的货梯称为大载荷货梯。大载荷货梯载荷大，常用于运送军工、航天和汽车等重型设备，这些设备在输送环节中，对振动等相对敏感，因此要求对货梯在工作中的振动进行分析，以满足货梯的减振需求。大载荷货梯的振动分析需考虑电梯曳引钢丝绳的时变刚度，导轨的支撑刚度的影响，这两者都是时变刚度，因此，曳引系统总体上是非线性系统。对于钢丝绳的时变问题，Zhu等[1]分别针对静态与运行状态提出了不同边界条件下电梯曳引钢丝绳的线性模型。于德介等[2]利用拉格朗日方程建立了1∶1电梯系统7自由度振动模型，提出了一种基于实测系统固有频率的电梯动力学模型修正方法；Kang等[3]分析轿厢内货物的质量以及轿厢所处位置与系统共振频率的关系，发现钢丝绳与轿厢的共振是导致系统垂直方向的振动主要原因。Mei等[4]建立了9 自由度曳引电梯模型，以电梯垂直振动加速度幅值为目标函数，对其运行状态参数和结构参数进行了优化。Qiu等[5]和Wu等[6]提出了一种基于能量的振动模型描述高速电梯的多向耦合特性，分析了结构与运动特性，结合运动能量、弹性势能用能量和虚功来描述振动特性。傅武军等[7]将轿厢-轿架之间视为刚性联接，建立了轿厢 5 自由度水平振动模型；并分别讨论了在不同导轨激励扰动下电梯轿厢的振动加速度响应。卢明阳[8]利用有限差分法求解动力学模型的微分方程，通过对比实验数据和仿真结果，得出导轨产生的随机激励是引起轿厢振动的主要因素之一。李醒飞等[9]和夏冰虎等[10]在此基础上进行了仿真和实验，验证了导轨不平度引发的刚度变化是轿厢横向产生振动的主要原因，并考虑导轨刚度的时变性建立了非线性水平振动系统模型，并给出了模型数值求解仿真结果。全文平等[11-12]充分考虑导靴刚度、阻尼以及摩擦等非线性特性，建立了轿厢-导靴-导轨动力模型，并给出了相关的振动方程。吴虎城等[13]针对电梯提升系统曳引钢丝绳的时变特性，改变曳引钢丝绳的提升质量、线密度及导靴刚度系数和阻尼系数获得不同参数下的轿厢横向振动响应。

上述学者的研究大多是针对客梯的，关于货梯的研究较少。课题组在上述学者研究的基础上，考虑了曳引梁对整个曳引系统的影响，曳引钢丝绳的时变特性，以及导轨不平顺性导致的刚度变化，建立了大载荷货梯曳引系统振动模型，并用Runge-Kutta法对振动方程进行求解，并进行了实验论证。最后课题组利用MATLAB仿真模拟曳引系统对货梯振动性能的影响，为货梯曳引系统振动特性的进一步分析提供了参考。

1 大载荷货梯曳引系统振动模型

1.1 曳引梁的刚度模型

曳引梁是承载曳引机的支撑部件。建立货梯动力学模型时，可以将曳引梁进行等效弹性[14]处理，与曳引梁的减振橡胶串联。曳引梁的弹性模量和抗弯截面惯性矩分别为Ec和Ic。曳引梁刚度模型如图1所示，且有：

图1 曳引梁刚度模型

其中，

(1)

式中：kx1为下曳引梁等效刚度，kx2为上曳引梁等效刚度，L为曳引梁长度，S为2块减振橡胶之间的距离，k为单根曳引梁的刚度。

假设2根曳引梁上的每块橡胶的刚度为kx3和kx4(每根曳引梁上放有2块相同的像胶)，kx5为单根曳引梁与底座橡胶的等效刚度。为了保证在静力作用下货梯曳引机不发生倾斜，必须满足每根曳引梁与其橡胶的等效刚度相同，即

(2)

这样，所有曳引梁及底座橡胶的总等效刚度为：

k1=2kx5。

(3)

1.2 曳引绳的变刚度模型

曳引绳是作为电梯曳引系统的重要组成部分，考虑到曳引绳由多根钢丝绳捻制而成，则有

(4)

式中：Eg为钢丝绳的弹性模量，L0为钢丝绳初始长度，A1为钢丝绳横截面积，N为曳引绳中钢丝绳的股数，LU为曳引绳由于运行工况升降变化的长度。

由于LU随电梯运行变化，k2也不断变化，使得曳引绳为变刚度系统。

1.3 导轨变刚度模型

导轨是安装在电梯井道中的2列垂直且对称的轨道，主要作用是控制着电梯轿厢的运行轨迹，保证其沿着轨道上下运动。在实际中，由于导轨支架的周期性分布[15]，导轨对导靴的作用力以及导轨变形呈现出周期性变化，即导轨的刚度发生周期性变化。为分析导轨刚度的变化规律，用SolidWorks软件依次在10 m长的导轨上插入连接板和导轨支架，建立导轨及支架系统的三维模型如图2所示。

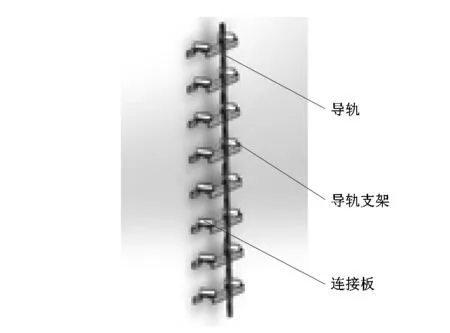
图2 导轨变刚度三维模型示意图

课题组按照合作企业的设计要求，设定2个导轨支架之间的间距为1.2 m。依照图3所示的导轨变刚度模型建立导轨变刚度动力学模型。

图3 导轨变刚度模型

图3中，点A，B为导轨上连续的2个导轨支架支撑点。假设滑动导靴运行到C点，可以看作在C点增加载荷F,规定向右为正。设AC长为a，BC长为b,由于C点施加了力F，则A点的反作用力为：

RA=Fb2(1+2a/s)/s2。

B点的反力：

RB=Fa2(1+2b/s)/s2。

可求得在C点施加力F后的挠度[15]：

(5)

式中：E为导轨的弹性模量，If为导轨的材料横截面对弯曲中性轴的惯性矩。

则点C的刚度kC为：

(6)

式中：Ed为导轨支架的弹性模量，Id为导轨支架的材料横截面对弯曲中性轴的惯性矩，Ld为导轨长度。

1.4 曳引系统振动模型

对于图4所示的大载荷货梯曳引电梯系统，考虑低速状况下曳引绳的横向振动对电梯系统影响不大，电梯振动系统可以看作主要由曳引绳、轿厢、轿架和导轨系统组成，为简化曳引系统振动建模，本研究中建模特作以下假设：

图4 曳引系统动力学模型

1) 不考虑钢丝绳质量和自由度，认为钢丝绳均匀、各向同性，是复合理想弹性体。

2) 多根钢丝绳视为具有等效截面的单根钢丝绳。

3) 轿厢与轿架刚性连接，视轿厢与轿架为一个具有质量和转动惯量的刚体[16]。

4) 将水平振动非线性系统简化为线性弹簧-阻尼系统。

根据牛顿第二定律，建立大载荷货梯曳引系统5自由度运动微分方程：

1) 曳引梁振动方程

(7)

2) 对重端Z方向振动方程

(8)

3) 曳引系统耦合振动微分方程

(9)

式中：m2为电梯轿厢质量，m为电梯负载质量，m3为对重端质量，μ为滑动摩擦因数，k4为左导轨与轿厢连结的刚度，k5为右导轨与轿厢连结的刚度。

4) 曳引系统Y方向振动方程为：

(10)

式中：Yr为曳引系统Y方向相对位移，Yg为曳引系统Y方向基础位移,c4为左导轨与轿厢连结的阻尼，c5为右导轨与轿厢连结的阻尼，θ2为轿厢的偏转角，e为右导靴至偏心的垂直距离。

5) 轿厢偏转角振动方程

(11)

式中：f为轿厢顶部中心至导靴的垂直距离，g为轿厢底部中心至导靴的垂直距离，c为导靴阻尼。

根据建立的非线性微分方程，利用四阶Runge-Kutta法对微分方程进行求解。曳引系统仿真流程如图5所示，其中T为当前仿真时间，Δt为MATLAB仿真时的步长。

图5 曳引系统仿真流程图

2 大载荷货梯曳引系统振动模型求解

2.1 MATLAB中模型参数设定

根据课题组提出的大载荷货梯曳引系统的振动模型，在MATLAB中使用四阶Runge-Kutta法编写程序进行大载货电梯曳引系统的仿真研究。与电梯曳引系统相关的参数会参考设计标准进行估算或者测量计算得出，部分曳引系统参数如表1所示。

表1 曳引系统参数表

2.2 仿真工况

电梯企业对曳引轮进行控制，给出的理想货梯运行曲线如图6所示。货梯在运行时，通过曳引机控制轿厢运输，选择合适的电梯运行曲线，可以减小货梯产生的振动以及缩短运行耗费的时间，提高安全性以及效率。课题组根据货梯实际运行曲线，模拟货梯系统仿真时的加速度函数与速度函数如下：

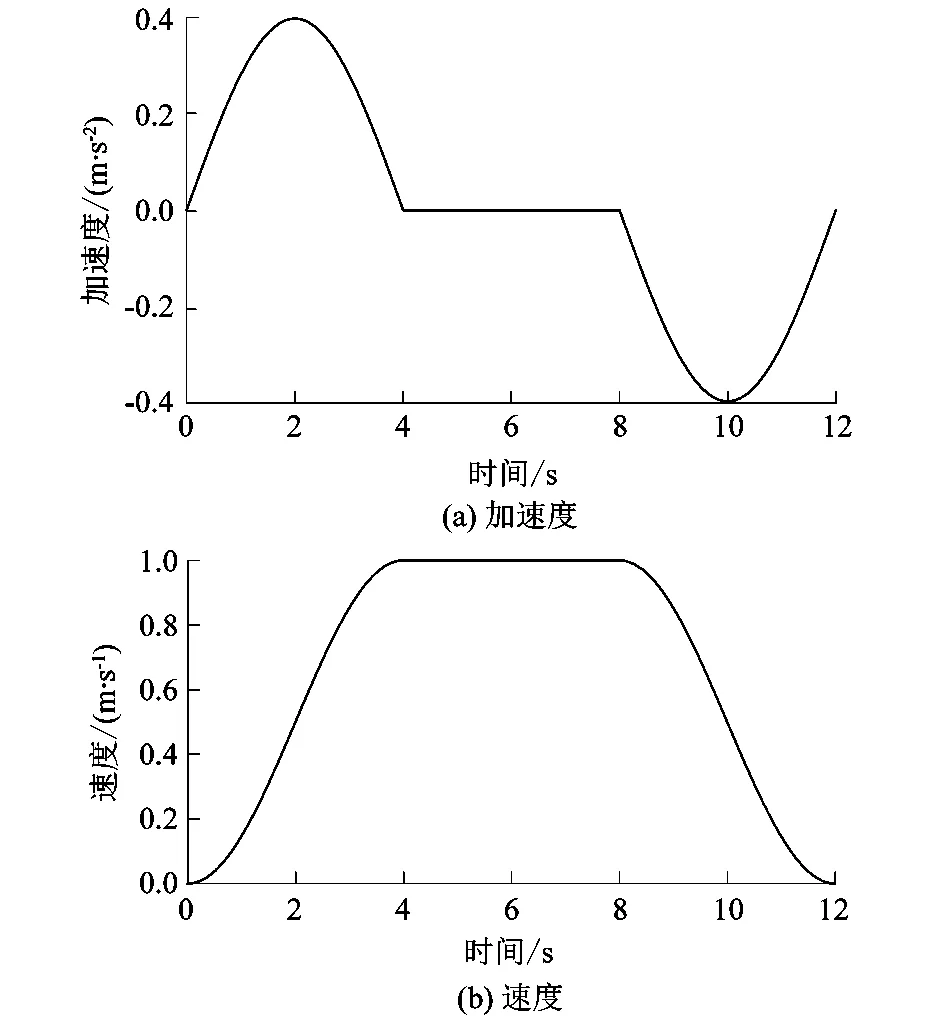
图6 货梯运行曲线图

(12)

(13)

式中：t为时间，s；a1为货梯加速度，m/s2；v为货梯运行速度，m/s。

钢丝绳的变化量：

式中：t0,t1分别为运行工况的起始时间和终止时间。

则导靴在导轨上的运行距离：

(14)

式中：td1为导靴从第1个导轨支架运行到第2个导轨支架间隔时间；以此类推，可知td2为导靴从第2个导轨支架运行到第3个导轨支架间隔时间。

图7所示为仿真模型中曳引系统各方向定义。由图可知，X正方向为曳引系统对应轿门侧方向，Y正方向为曳引系统对应右侧导轨方向，Z正方向对应曳引系统的曳引机位置方向。

图7 曳引系统各方向定义

2.3 MATLAB模型仿真结果

将式(12)和(13)作为模型工况函数输入，设置载荷、初始位移及其初始速度为0，得到图8～9所示曳引系统空载上下行振动加速度响应图。由图8～9可知，曳引系统Z方向振动加速度响应最大值达到0.54 m/s2，上行工况的振动比下行工况要激烈。这是因为制动受到冲击时是整个系统产生振动最恶劣的情况，而上行时曳引钢丝绳缩短，靠近曳引机，导致抵抗振动的能力减弱，所以上行接近顶层时系统振动会比在下行接近底层时更剧烈。空载、半载和满载工况下Z方向仿真振动最大加速度数据如表2所示。

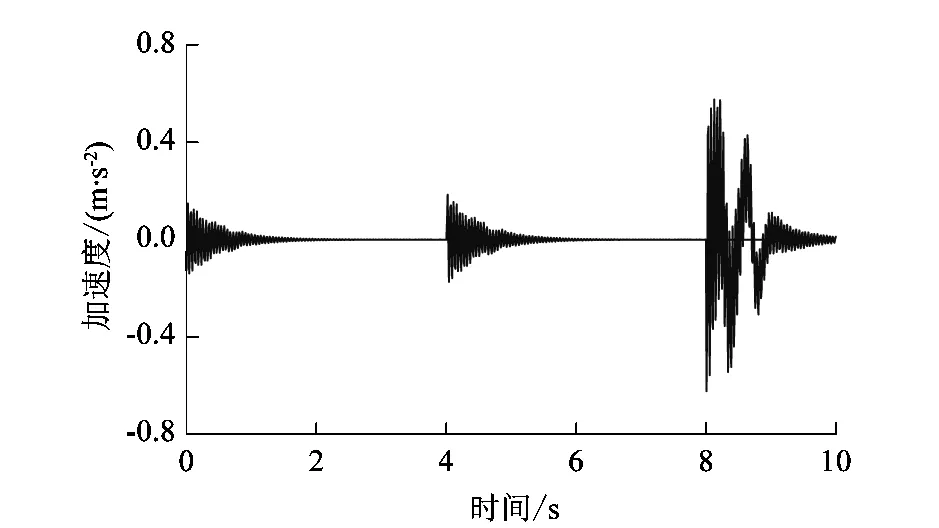
图8 空载上行Z方向振动加速度响应图

图9 空载下行Z方向振动加速度响应图

由表2可知，货梯系统在半载上行工况下Z方向振动加速度响应最大值达到0.83 m/s2，货梯系统在半载下行工况下Z方向振动加速度响应最大值达到0.73 m/s2，货梯系统在满载上行工况下Z方向振动加速度响应最大值达到1.14 m/s2，货梯系统在满载下行工况下Z方向振动加速度响应最大值达到0.94 m/s2，随着载荷的增大，货梯系统的最大振动加速度幅值也随之增大。

表2 Z方向仿真最大加速度数据表

3 实验验证

3.1 测试实验平台

某公司对15 t大载荷货梯进行了振动测试实验。实验所用到振动测量分析仪器亿恒多输入多输出(MIMO)振动控制器，用多DSP并行处理技术和分布式模块化设计，采用24位分辨率的ADC/DAC，系统控制动态范围达到90 dB，信噪比>100 dB，采样频率可扩展至20 480 Hz。货梯的数据采集仪器如图10所示。

图10 实验数据采集仪器图

传感器选用ZC1002LS ICP/IEPE250g三轴加速度传感器，此传感器采用具有压电效应的材料压电陶瓷，压电陶瓷晶体感受到系统产生的加速度而在晶体表面展现出电荷量，拥有无源、频响宽、灵敏度高的特点,使用频率范围为0.5～5 000.0 Hz，电压灵敏度为50 mV/g，最大量程为100 g。

3.2 实验布置及实验结果分析

为记录曳引机基于运行工况产生的激励与导轨对系统产生周期激励对货梯系统造成的振动，将三向加速度传感器放置于曳引机机座位置以及轿架主梁侧面位置,具体如图11～12所示。

图11 大载荷货梯振动实验示意图

图12 三向加速度传感器实物布置图

课题组在电梯处于空载、半载和满载3种载荷工况和上下行工况下进行振动测试，并记录实验数据。电梯上行与下行运行时间均约为10 s，最大速度为1 m/s。记录提取实验数据，使用MATLAB进行实验数据的处理和分析。空载时曳引系统振动测量曲线如图13所示。

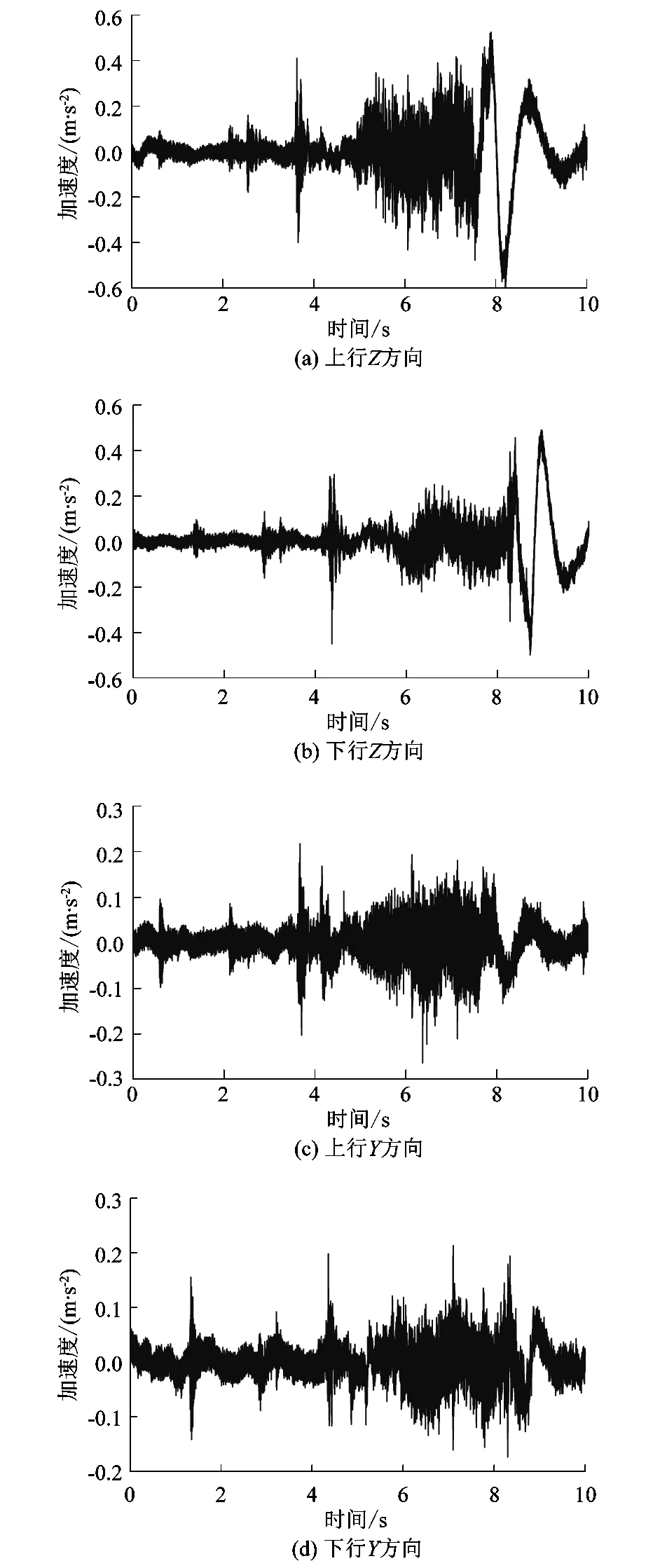
图13 空载工况下曳引系统振动实验测量曲线

根据实验可以得到曳引系统振动测试数据，实验与仿真结果对比如表3所示。

表3 曳引系统Z方向统实验与仿真结果对比

从实验与仿真结果对比可以得到以下结论:

1) 上行工况的振动幅度比下行工况振动幅度分别在3个载荷工况下大18%，16%和26%。这是因为当电梯上行时，曳引钢丝绳受到的力为系统重力以及加速度产生的惯性力之和；而下行时，则为两者之差。即上行曳引钢丝绳载荷大于下行，使得振动幅值增加。

2) 系统处于启动阶段时，Z方向的振动加速度并没有非常激烈，而是随着速度的增大而呈现增大趋势；加速度越大，系统的振动越激烈，当加速度到达极值点时，会有一个剧烈的振动响应，但整个运动过程并不是一直产生振动，在平稳运行阶段，因为阻尼的作用振动加速度不断进行衰减。

4 大载荷货梯振动工况影响分析

4.1 不同单跨间距工况

企业生产安装货梯时，导轨支架的疏密对货梯生产安装成本有一定影响，课题组对货梯不同间距的导轨支架对振动的影响进行分析，按照1.4，1.2和1.0 m的间距设置导轨支架，其振动响应如图14～15所示。

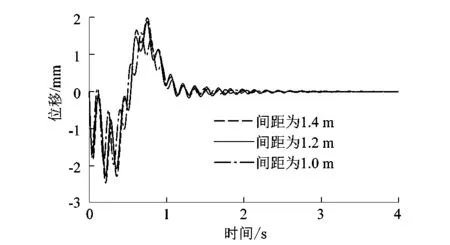
图14 导轨支架不同间距时曳引系统振动位移

图15 导轨支架不同间距时曳引系统振动加速度

由图14～15可以看出，当导轨支架间距1.4 m时，曳引系统最大振动位移为2.46 mm，最大振动加速度为0.688 m/s2；当导轨支架间距为1.2 m时，曳引系统最大振动位移为2.26 mm，最大振动加速度为0.585 m/s2；当导轨支架间距为1.0 m时，曳引系统最大振动位移为1.95 mm，最大振动加速度为0.514 m/s2。导轨支架间距减小，导轨刚度增大，振动位移与加速度随之减小。说明电梯的导轨支架间距减小，导轨颤动减弱，此时电梯更快地进入平稳运行阶段,反映了仿真模型整体振动特性的改善。因此，针对大型载货电梯，可以减小导轨支架间距，来达到减振的目的；但间距的减小会造成导轨支架数量的增加，进而导致工程成本的增加，所以需要选择合适的导轨支架间距来控制振动和成本。

4.2 货物冲击工况

大载荷货梯轿厢面积大，高度高，货物在轿厢内处于堆叠状态，由于堆叠状态造成重心不稳可能导致货物的部分跌落或堆叠倒塌。根据冲量定理，货物跌落的冲量为：

(15)

式中：h′为货物跌落前的高度；m4为跌落货物的总质量；t1，t2为冲击起始时间以及结束时间；F为货物对曳引系统的冲击力。

货物冲击力F(t)分布如图16所示。

图16 货物冲击力示意图

冲量作用于轿厢底板，假设货物下落与轿厢底板碰撞后不弹起，即碰撞是塑性的，碰撞作用时间Δt=0.1 s，冲击力

(16)

式中：α=0.05，β=0.012；e=2.718 28；Fmax为冲击力最大值。

将F(t)加入式(9)，并用Runge-Kutta法求解。设跌落货物m4=500 kg，货物从2 m高度跌落,得到货梯处于不同高度时对货物跌落造成系统的冲击的影响结果，如图17所示。

图17 不同高度的系统振动位移曲线

由图17可知，当货物跌落时电梯轿厢位置位于底层时，其曳引系统最大振动位移为11.5 mm，曳引绳伸长应变为0.115%，冲击结束后在接近7.0 s时进入平稳状态；轿厢位于3 m高度时，其曳引系统最大振动位移为9.62 mm，曳引绳伸长应变为0.137%，冲击结束后在5.5 s时进入平稳状态；轿厢位于6 m时，其曳引系统最大振动位移为7.19 mm，曳引绳伸长应变为0.180%后在4.0 s时进入平稳状态。随着轿厢位置的不断增高，曳引系统的刚度和固有频率不断增大。虽然受到冲击后的最大位移不断减小，但曳引绳伸长应变不断增加，钢丝绳抵抗冲击的能力也不断减弱。

本研究货梯选用的曳引绳直径为16 mm，其每根曳引钢丝绳最小破断负荷[17]为52.8 kN，系统承载负荷为6根曳引钢丝绳，则曳引绳总的破断载荷为316.8 kN。

曳引钢丝绳在受到冲击作用时，其横截面上受到的载荷包括冲击载荷F(t)，以及轿厢和货物的重力静载荷，其中静载荷[18]:

(17)

式中：r为曳引比，my为曳引绳质量。

根据上面计算得到的曳引钢丝绳的伸长量(最大位移)和弹性模量，可以计算钢丝绳应力：

(18)

曳引绳最小安全系数：

(19)

式中:Nequiv为曳引系统滑轮的等效数量，Dt为曳引机曳引轮直径，dr为曳引绳直径。

根据曳引机以及钢丝绳型号，得到最小安全系数为20.94。

设置电梯运行总高度为10 m。由表4可得，当货梯处于底层时，最大应力值为83.1 MPa，安全系数为破断应力值与最大应力值之比，其值为9.23；当货梯位于3 m层高时，最大应力值为99.4 MPa，安全系数为7.72；当货梯位于6 m高度时，最大应力值为130.0 MPa，安全系数为5.90。最大许用应力值不随着高度而变化，最大应力值随着运行高度的上升不断增大，安全系数随着高度增加逐渐减小。曳引绳最小安全系数为20.94，而货物跌落造成冲击使安全系数远小于最小安全系数，导致曳引系统处于危险状态，不能保证曳引系统的安全工作。

表4 货物跌落冲击结果

5 结论

课题组针对大载荷货梯系统运行工况复杂，载荷质心随机性强的问题，建立了一种货梯曳引系统的非线性动力学模型，利用Runge-Kutta法迭代求解模型，与大载荷货梯振动实验平台测试的结果进行对比，验证了模型的可靠性，为企业研究大载荷曳引系统货梯的振动特性提供了参考。

仿真结果表明：上行工况的振动比下行工况要激烈，制动受到冲击时是整个系统产生振动最恶劣的情况；随着载荷的增大，货梯系统的最大振动加速度幅值也随之增大；导轨支架的疏密度会对轿厢振动有一定的影响，过疏的支架密度会导致振动加剧，而过密的支架会增加企业的制造、安装成本；货物在堆叠货物不慎掉落时，会产生极大的冲击作用，可能会导致曳引系统的破坏。因此，设计制造大载荷货梯时，必须要着重考虑到电梯各种不利情况，提出合理的减振方案。

课题组对货梯建模时，忽略了制动盘摩擦力、钢丝绳质量、钢丝绳横向扰动力等参数，对一些动力学参数做了假设，并不是非常精确。进一步的研究可以建立更精准的动力学模型进行仿真分析，在优化模型时，可以采取基于多目标优化算法，以期达到理想的结果。