基于多关联参数特征子空间的纺纱质量波动预测
2022-10-31张守京
李 哲, 胡 胜, 张守京, 李 文
(西安工程大学 机电工程学院, 陕西 西安 710600)
纺纱过程作为棉纺生产过程的关键环节,其纱线质量的好坏直接决定了后续工序的成型效率和成品织物的加工质量。但由于纺纱生产过程影响因素多、监测维度广,纺纱工艺参数与纱线质量间呈现复杂非线性等特征[1],使得纺纱质量波动模型难以建立。同时,通过大量试纺和专家经验来调节加工工艺参数和配棉方案提高纱线品质的方式,势必会造成大量时间和原材料的浪费,不符合智能制造背景下产品质量在线控制的内在需求。因此,如何建立基于生产过程关键工艺参数的纺纱质量波动预测模型对改进纱线质量、提高过程稳定性和优化决策支持具有重要价值。
国内外学者针对此问题进行了大量研究并取得一系列成果:张羽彤等[2]提出一种灰色关联分析法对小容量样本中的工艺参数进行了优选,并采用BP神经网络建立小样本精梳毛纺纱线质量预测模型对条干不匀率和断裂强度进行预测。熊经纬等[3]针对复杂纺纱过程中成纱断裂强度难以预测的问题,提出一种基于粒子群优化算法优化BP神经网络的成纱断裂强度预测方法。为进一步提高BP神经网络在纱线质量预测时的精度和训练速度,查刘根等[4]提出具有双隐层的4层BP神经网络来进行棉纱成纱质量预测。吴志刚等[5]提出一种基于思维进化算法优化BP神经网络的细纱断裂强度预测方法。马创涛等[6]针对传统BP神经网络预测模型泛化能力弱且预测精度低的问题,提出了一种基于烟花算法改进BP神经网络的预测模型。张晓侠等[7]提出基于BP神经网络及其改进算法对织机效率进行预测。宋楚平等[8]针对纱线生产中工艺难以优化以及质量控制过于依赖专家经验的问题,提出一种基于遗传算法优化的支持向量机纱线质量预测模型。胡胜等[9]为及时挖掘纺纱生产过程纱线质量的异常波动并进行纱线质量的稳定性判定的问题,提出了一种基于变点识别的纺纱过程质量波动异常预警方法。Doran等[10]利用纤维质量和纺纱参数,提出了人工神经网络和支持向量机模型来预测包芯纱的质量特性。Hu等[11]针对浅层神经网络预测精度较低的问题,提出基于卷积神经网络与广义回归神经网络相结合的精纺毛纱质量预测模型。Ghanmi等[12]提出混合神经网络模糊专家系统模型对转杯纱的质量进行整体性能预测。
以上文献研究表明:目前针对纱线质量预测的研究主要集中在使用浅层神经网络模型对纱线质量进行建模,而通过分析纺纱多关联参数相关性进行纱线质量预测相对较少。鉴于此,课题组基于特征子空间的深度信念网络多关联参数纱线质量预测方法,首先分析影响纱线质量的关联参数之间关系,构造表征纱线质量波动的特征子空间,实现原始多关联参数的维度约简;然后构建基于特征子空间的深度学习纱线质量预测模型,最后通过实例验证所提方法的有效性。
1 基于深度信念网络的纺纱质量波动预测框架
纺纱生产过程波动的稳定性是影响纱线品质的关键因素,对纺纱时质量波动进行预测是掌握纱线质量稳定性的有效途径。在生产过程中通过智能监测系统采集高维的海量数据,这些数据的变化轨迹不仅体现了纺纱过程变化趋势,而且表征了纱线质量波动程度。课题组提出的基于深度信念网络的纺纱质量波动预测框架包括2个关键技术:①对纺纱过程的多关联参数数据进行相关性分析,约简质量数据维度,剔除冗余信息,重构纱线质量波动的主元特征子空间;②探求多关联参数特征子空间与纱线质量波动的非线性影响关系,构建深度信念网络对特征子空间的数据信息进行深度特征提取,并通过误差反向传播进行有监督全局微调实现纱线质量深度预测建模。基于深度信念网络的纺纱质量波动预测框架如图1所示。

图1 基于深度信念网络的纺纱质量波动预测框架
2 纺纱过程多关联参数特征子空间建模
在构建纺纱过程纱线质量波动预测模型时,由于影响纱线质量的参数多且相互关联[13],使得纱线质量随这些参数变化而动态波动。典型的情况就是即使每个参数都在正常范围内波动,其实际纱线质量也有可能产生异常波动,使得对纱线质量进行精准预测变得困难。为此,首先分析纱线多关联参数之间关系,采用主成分分析算法将原始多维相关参数的高维空间映射到互不相关且能够代表原始特征的低维特征子空间,提取能够反映纱线质量波动的主元特征子集。其本质是将k维影响纱线质量的关联参数特征数据映射到p维空间,去除原始关联参数的冗余性,实现纺纱多关联参数维度约简。具体步骤如下:
对于影响纱线质量的多关联参数X={x1,x2,L,xk},其中,xi∈Rn,n为样本数量,k为多关联参数维度。首先计算其标准化处理后的协方差矩阵A=(aij)k×k,其中,aij表示第i和第j个参数的相关系数。
(1)
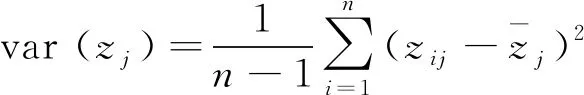
然后求解协方差矩阵A对应的特征方程|λE-A|=0,得到其特征值λ按其值大到小排序λ1≥λ2≥L≥λk以及对应的特征向量W=[w1,w2,L,wk],其中E为单位矩阵。
据此,得到多关联参数主元特征空间可表示为X′=ZW。经过相关性分析后形成的主元特征空间有效剔除了原始数据信息的冗余性,在保证特征维度正交的同时有效去除原始多关联参数的相关性。
为有效提取纺纱参数信息并降低预测模型的输入复杂度,基于上述主成分分析结果计算每个主成分贡献率大小,并求前p个主成分的累积贡献率,由下式计算:
(2)
当累积贡献率达到90%时,对应的前p个主成分组成的特征空间即可反映原始k维纺纱参数的绝大部分信息,据此重构得到原始纺纱参数的特征子空间,即为:

(3)
其中:W′=[w1,w2,L,wp];Z=(zij)n×k。
式中Z为多关联参数X的标准化矩阵。
经过相关性分析重构得到的特征子空间不仅有效保留了原始样本数据空间的特征信息,而且在去除原始多关联参数相关性的同时保证了特征维度正交特性,将其作为纱线质量波动预测模型的输入,实现了维度约简的同时有效降低了纱线质量波动预测模型的复杂度。
3 构建深度学习的纺纱质量预测模型
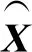
(4)
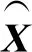
在纺纱生产过程中,纱线的条干CCV值直接反映了纱线粗细程度,是度量纱线质量的重要指标。CCV值越大说明纱线的粗细越不均匀,会对纱线的断头率造成影响。影响纱线条干CCV值的因素包含了毛条含油量、粗纱捻系数、毛条回潮率、纤维直径及细纱车速等众多影响质量的参数。深度信念网络是由多个受限波尔兹曼机叠加而成的深度学习算法[14],在非线性系统建模中表现出优异的拟合能力。鉴于此,本节探求多关联参数与纱线质量特性间的非线性关系,构建纺纱多关联参数与纱线质量指标的深度信念网络预测模型,如图2所示。纱线质量预测模型分为RBM逐层无监督训练和BP层有监督微调两部分,底部由4层RBM堆叠对特征子空间的数据信息进行深度特征提取,顶部BP神经网络通过误差反向传播进行有监督全局微调。DBN通过多层特征映射和逐层传递建立起多关联参数与纱线质量指标之间的非线性关系,实现对纱线质量智能预测。

图2 基于DBN网络的纺纱质量预测结构
每一个RBM是由可视层v(v={v1,v2,L,vn})和隐藏层h(h={h1,h2,L,hm})组成的双层网络结构,层间神经元通过权重wij和偏置相连,但同一层的神经元之间相互独立并且只有激活和未激活2种状态,由{1,0}表示。首先,RBM是一种基于能量的模型[15-16],可以利用能量函数将RBM表示为:
(5)
式中:θ={wij,ai,bj}分别代表可视层与隐藏层的连接权重、可视层和隐藏层的偏置值,vi和hj分别代表可视层和隐藏层神经元的状态,n和m分别代表可视层和隐藏层中的神经元个数。
其中,较低的能量表示网络处于较为理想的状态,即纱线质量预测模型的误差较小。对能量函数正则化和指数化计算得出可视层与隐藏层(v,h)的联合概率分布为:
(6)

由于RBM层内各神经元之间激活状态彼此独立的结构性质,即在给定可视层神经元状态时可以计算出隐藏层第j个神经元被激活的概率;相应地,当给定隐藏层神经元状态时可由式(7)算出第i个神经元被激活的概率。
(7)
式中σ为激活函数。
因此,构建纱线质量预测模型就是要寻找每层RBM的连接权重和偏置的组合θ={wij,ai,bj}。对于数量为N的训练样本输入预测模型,θ可采用最大似然函数表示:
(8)
对RBM逐层求解对数似然函数的负梯度得θ={wij,ai,bj}组合,更新规则为:
(9)
式中:〈〉data为训练样本期望;〈〉recon为重构模型定义分布,η为学习速率。
预测模型的无监督训练阶段利用贪婪算法对RBM逐层进行训练,并将上一个RBM训练后的隐藏层输出作为下一个RBM可视层的输入,以此实现每一层的RBM最优。在有监督训练阶段采用BP算法对RBM4所提取的深度特征进行预测,基于预测误差调整网络参数,确保DBN预测结构的整体最优。
4 实例分析
为验证所提方法的有效性,以某精纺毛纱生产过程为例进行纺纱多关联参数质量波动预测方法的验证。精纺毛纱作为纺纱过程的重要环节,其纱线质量的好坏直接决定纺纱的合格率。若能在纺纱生产之前对纱线质量进行预测分析,则有利于提高纱线成品质量。进行实例分析时,选取毛条含油、毛条回潮率、纤维直径以及细纱转速等10个关键影响因素作为输入,同时选取纱线CCV值作为纱线质量指标进行分析。选取参考文献[17]表5-4中某纺纱厂75组精梳毛纱生产数据进行纱线质量预测方法的验证,其部分样本数据如表1所示。
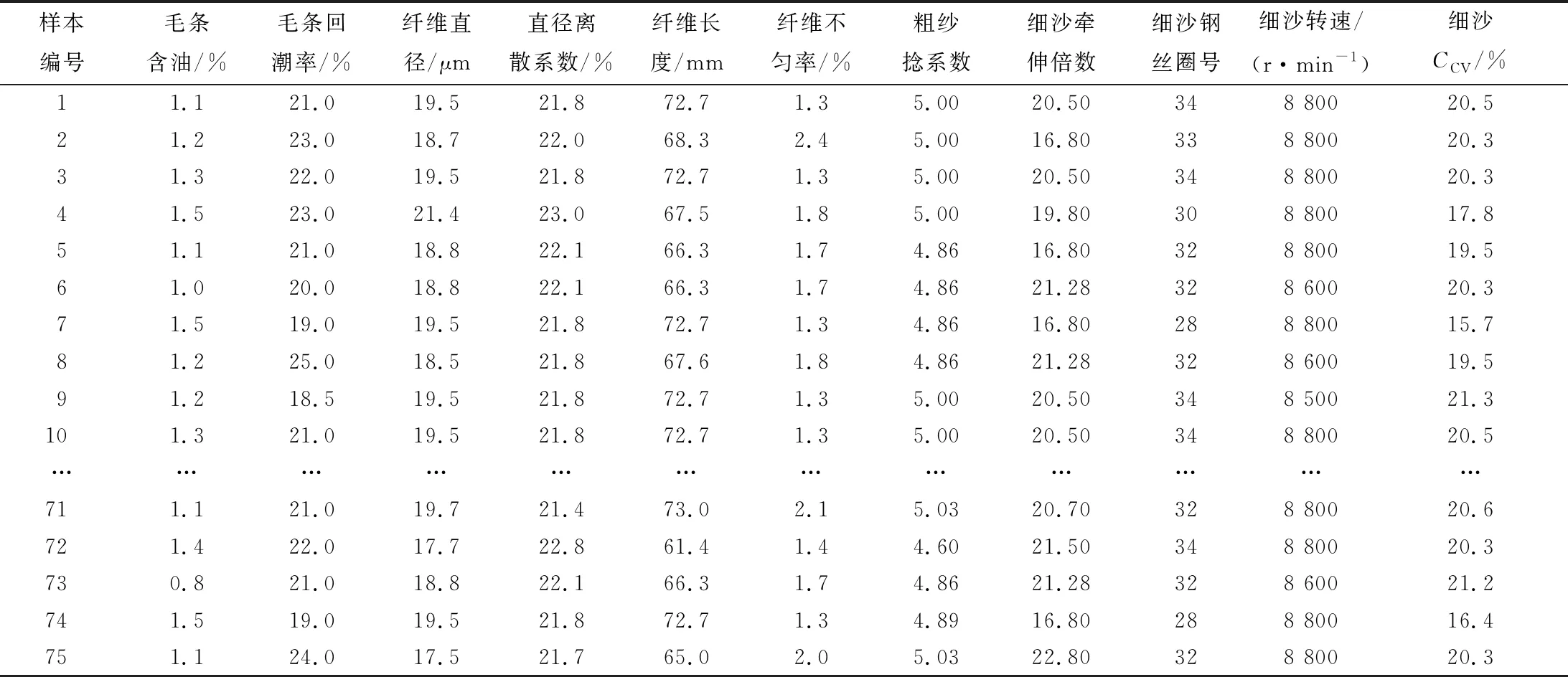
表1 部分精梳毛纱质量数据
4.1 多关联参数纺纱质量相关性分析
为挖掘能够反映纺纱过程质量波动的多关联参数信息,首先分析75组多关联参数的相关性,采用主成分分析算法进行维度约简。图3给出了相关性分析后方差贡献率以及累积贡献率的计算结果。
由图3可知,前7个主成分的累积贡献率达到90.925 9%,因此选取其主成分特征集作为表征纱线质量原始样本数据特征信息,基于此构建影响纱线质量的关键特征子空间,实现原始特征的维度约简。
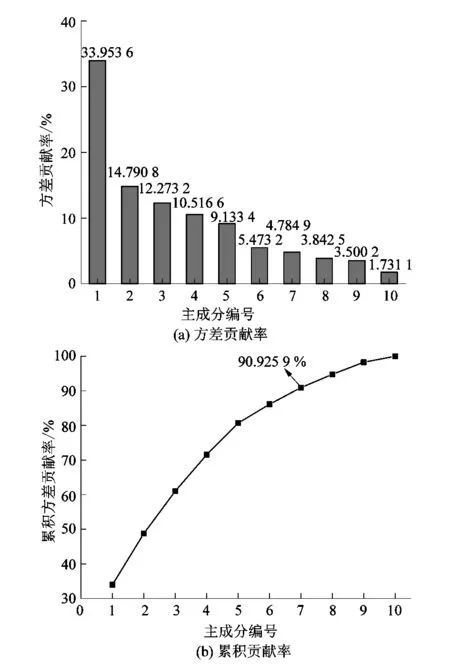
图3 相关性分析后的方差贡献率与累积贡献率
4.2 纺纱质量波动预测
进行纱线质量预测建模时,首先选取维度约简后子空间的前70组主元特征样本用于纱线质量预测模型的训练,同时提取后续5组主元特征作为测试数据集对构建的纱线质量预测模型进行测试。其中训练深度信念网络预测模型时的相关参数设置如表2所示。

表2 训练深度预测模型时的算法参数设置
然后,待深度信念网络预测网络模型训练结束后,使用测试集数据进行纱线质量波动预测,预测结果如图4所示。
由图4可以看出,基于多关联参数特征子空间的深度信念网络纱线质量预测结果与实际值几乎一致,说明建立的纱线预测模型精度较好,提出的方法在纺纱质量控制过程中展现出了良好的预测效果。为进一步验证所构建预测模型PCA-DBN的有效性,分别选取DBN网络模型和PCA-BP模型进行对比,试验时采用相同规模训练样本集进行训练,并作用于相同的测试集。为定量评价预测模型性能,分别选取平均绝对百分比误差(EMAP)、均方根误差(ERMS)和平均绝对误差(EMA)衡量模型预测值与真实值的偏差,在多种试验条件下的不同结构模型的预测误差如表3所示。
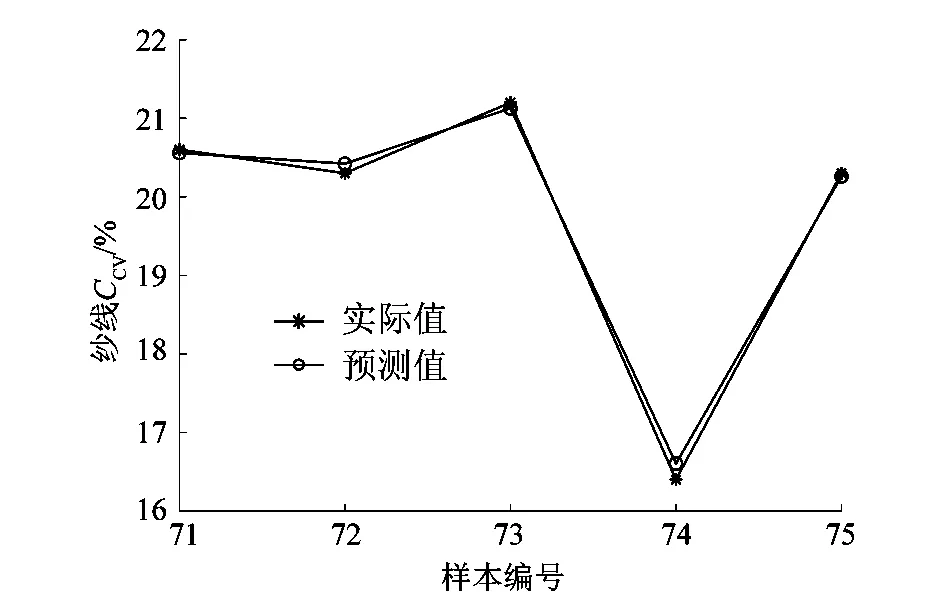
图4 纱线质量预测值与实际值对比
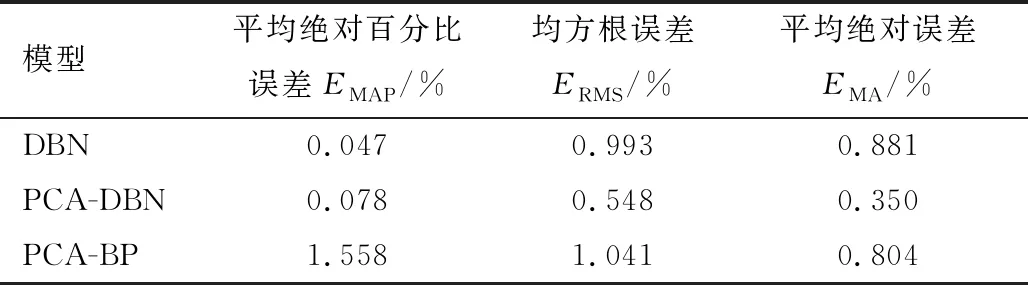
表3 不同结构模型的纱线质量预测结果对比
从表3可以看出,DBN模型由于没有考虑纱线多关联质量参数的影响,其预测结果相比维度约简预测模型(PCA-DBN)具有更大的偏差;进一步考虑多关联参数相关影响后,由于深度信念网络相比浅层BP神经网络具有较强的特征提取能力,所以其预测结果比PCA-BP模型能够获得更加准确的预测效果。表明纱线质量预测精度得到了提升,所构建模型预测效果显著。
5 结论
针对纺纱过程中多关联参数变化导致纱线质量波动难以预测的问题,课题组提出了基于深度信念网络的纺纱质量波动预测方法。首先利用主元分析方法对纺纱过程的多关联参数进行约简数据维度,获取能够表征质量波动的主元特征向量作为预测模型输入;然后通过构建面向特征子空间的深度信念网络纱线质量预测模型,有效拟合出多关联参数特征子空间与质量指标的非线性关系,实现对纱线质量指标的预测。以某纺纱生产过程为例进行验证,结果表明深度信念网络算法在预测精度准确性方面相比于浅层神经网络误差较小,为纺纱生产决策参数稳健优化提供了参考。
