耦合传热与润滑影响的涡轮增压器浮环轴承动态特性分析

毛驭华

（200093 上海市 上海理工大学 机械工程学院）

0 引言

涡轮增压器和浮环轴承分别作为主要的运动部件以及润滑部件，对发动机稳定工作起着至关重要的作用[1]。过去几十年，国内外对涡轮增压器转子—轴承系统方面进行了深入的研究。刘张飞[2]等人运用DyRoBes 软件和有限元差分方法得到了油膜压力以及浮环轴承油膜动力特性系数的变化规律；沈那伟[3]等人求解Reynolds 方程获取浮环的油膜压力，计算浮环轴承-转子临界转速和不平衡；Zhao[4]等人使用DyRoBes 有限元分析软件对涡轮增压器转子的临界转速和频谱图进行了分析，但是他们都没有考虑高温废气传热对涡轮增压器转子-轴承系统的影响；Gunter[5]等人使用DyRoBes 软件对含浮环轴承增压器转子进行了线性和非线性动力学分析，但将浮环轴承内外层油膜黏度假定为常值，造成了假设与实际情况相差很大的结果。

综合上述可知，国内外很多学者都采用将复杂问题简化处理的方法，往往与实际情况相差较大，因此本文基于某型号涡轮增压器开展转子-轴承系统动力学的仿真计算和试验研究，通过建立理论模型对浮环轴承润滑性能进行计算，基于转子动力学软件对涡轮增压器转子-轴承系统进行动力学分析，基于高速动平衡机与多功能气动试验台开展涡轮增压器转子动力学性试验。

1 涡轮增压器浮环轴承润滑和传热分析

1.1 浮环轴承润滑模型

用hi，ho分别表示浮环轴承的内外层油膜厚度。文中下标i为浮环内膜，o为浮环外膜。采用著名的雷诺（Reynolds）方程描述静载荷作用下浮环轴承内外层油膜的润滑特性，其中忽略了油膜的体积力和惯性力的影响，浮环轴承内外层油膜厚度的计算公式如下：

式中：ci，co——内膜和外膜的半径间隙；φi，φo——内膜和外膜的偏位角。

1.2 增压器传热模型分析

涡端和涡轮轴是涡轮增压器轴承体热量的主要来源，传递热量主要为热传导和流固共轭传热方式。

热传导公式

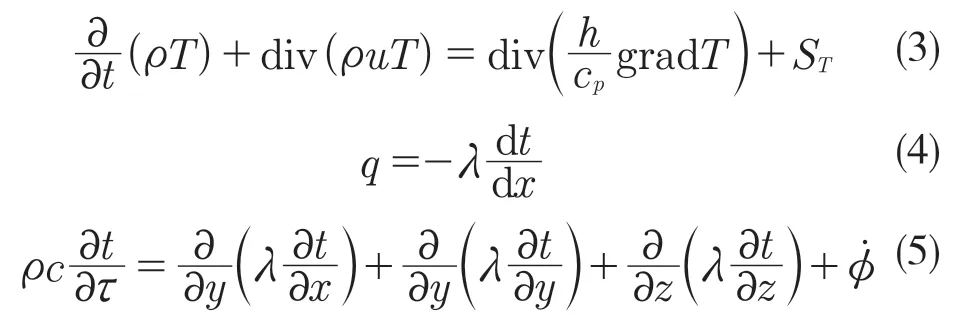
本研究中的流固共轭传热主要是润滑油介质与润滑油流道交界面之间的传热，以及隔热罩中空气夹层与轴承体交界面之间的传热。联立牛顿冷却公式及傅里叶定律可求得交界面处的表面传热系数[6]：

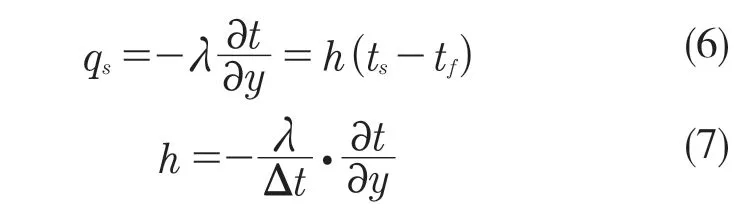
1.3 浮环轴承润滑模型计算分析

选择代号为SAE30 的润滑油，该种润滑油性能较好，能够在复杂的环境中保持较高的稳定性。图1 为该种润滑油的温黏曲线关系。

图1 SAE30 润滑油温黏曲线Fig.1 Temperature viscosity curve of SAE 30 lubricating oil

对浮环轴承润滑和传热理论进行分析并结合涡轮增压器的正常工作转速范围，选取19 个涡轮增压器工作转速点，分别在计入和不计入传热影响时对浮环轴承润滑性能进行分析，得到涡轮和压气机两端浮环轴承内外层黏度随着转速变化的关系曲线。图2 为浮环轴承内外层油膜黏度图像。从图2 中可以发现，随着工作转速的升高，计入传热影响时的黏度明显小于不计入传热影响时的黏度。

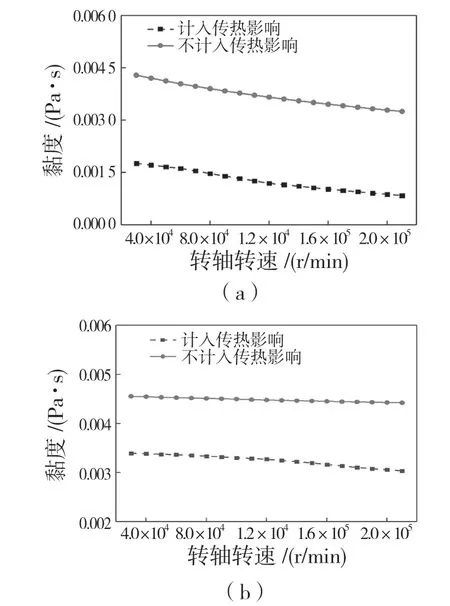
图2 浮环轴承内、外层油膜黏度Fig.2 Oil film viscosity of inner and outer layer of floating ring bearing

1.4 浮环轴承内外层油膜动力特性系数计算

浮环轴承内外层油膜的动力特性系数指的是油膜刚度和油膜阻尼。以涡轮端浮环轴承为例，在10 000～210 000 r/min 之间选取了11 个工作转速点，通过相关公式计算内油膜总刚度和总阻尼，如图 3 所示。可以看出，计入传热影响后，浮环轴承的动力特性系数发生了显著的变化。

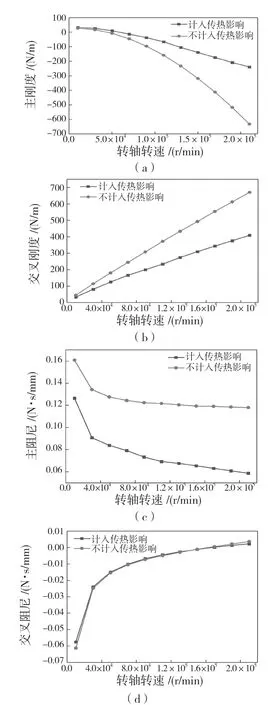
图3 涡轮端浮环轴承油膜动力特性系数Fig.3 Oil film dynamic characteristic coefficient of turbine end floating ring bearing

2 计入传热时涡轮增压器浮环轴承动态特性分析

基于DyRoBes 建立了转子-轴承系统的有限元模型后，对转子-轴承关键参数进行计算和分析，以初步验证转子模型的准确性。根据建立的模型，可以获得转子-轴承系统的关键参数如表1 所示。

表1 涡轮增压器转子-轴承系统关键参数Tab.1 Key parameters of turbocharger rotor-bearing system

由表1 中可知，转子系统模型整体长度为102.98 mm，转子系统总质量为73.6 g，该数据与转子系统实际尺寸以及质量误差在1%以内，可以初步认为模型是可靠的。对转子-轴承系统的静态特性分析结果如图4 所示。

图4 涡轮增压器转子-轴承系统静态变形与应力Fig.4 Static deformation and stress of turbocharger rotor-bearing system

2.1 涡轮增压器转子-轴承系统不平衡响应分析

不平衡是转子系统的主要故障之一，通过对转子不平衡响应分析，可以确定转子系统是否可以安全运行[7]。本研究中对涡轮增压器转子做了动平衡试验，根据试验结果得到了压端螺母和压端前缘的不平衡量，分别为0.075 g·mm∠12°（结点1）和0.15 g·mm ∠105°（结点7）。在模型中设置不平衡量后，进行10 000～240 000 r/min 转速范围内的稳态同步响应分析，获得了压端结点1、压端浮环轴承结点14、涡端浮环轴承17 以及涡端结点21 处的同步响应曲线如图5 所示。

如图5 所示，计入传热影响时，各个观测结点位置的最大不平衡响应振幅和转轴转速均大于不计入传热影响时，这是因为在计入传热影响后，浮环轴承内外层油膜的实际黏度会更小，使得支承刚度和阻尼发生很大变化，从而导致转子的振动会加剧，振动响应值变大。

图5 涡轮增压器转子-轴承系统各结点处的振动同步响应曲线Fig.5 Synchronous response curve of vibration at each node of turbocharger rotor-bearing system

2.2 涡轮增压器转子-轴承系统非线性动力学分析

高转速下工作时，浮环轴承中的油膜力具有比较强的非线性特性，因此需要对涡轮增压器转子-轴承系统进行非线性动力学分析。根据动平衡试验中得到的不平衡量，分别在结点1、7 两处设置0.15 g·mm ∠105°（结点1），0.075 g·mm ∠12°（结点7）的虚拟不平衡量，计入传热影响，并在10 000，150 000 r/min 转速下进行分析，得到了如图6、图7 所示的转子的运动轨迹图。

由图6 和图7 可知，在10 000 r/min 时，计入传热和不计入传热两种情况下转子的运动轨迹均呈现线性且振幅较小；而在150 000 r/min 时，转子在高转速下具有较强的非线性特性且振动响应比较剧烈；计入传热影响效应时，浮环轴承润滑特性更接近实际情况，浮环轴承内外层油膜黏度更低，转子在高转速下的振动响应明显大于不计传热时。

图6 计入传热影响时转子在10 000 r/min 和150 000 r/min 下的运动轨迹Fig.6 Rotor's motion trajectory under 10 000 r/min and 150 000 r/min with influence of heat transfer taken into account

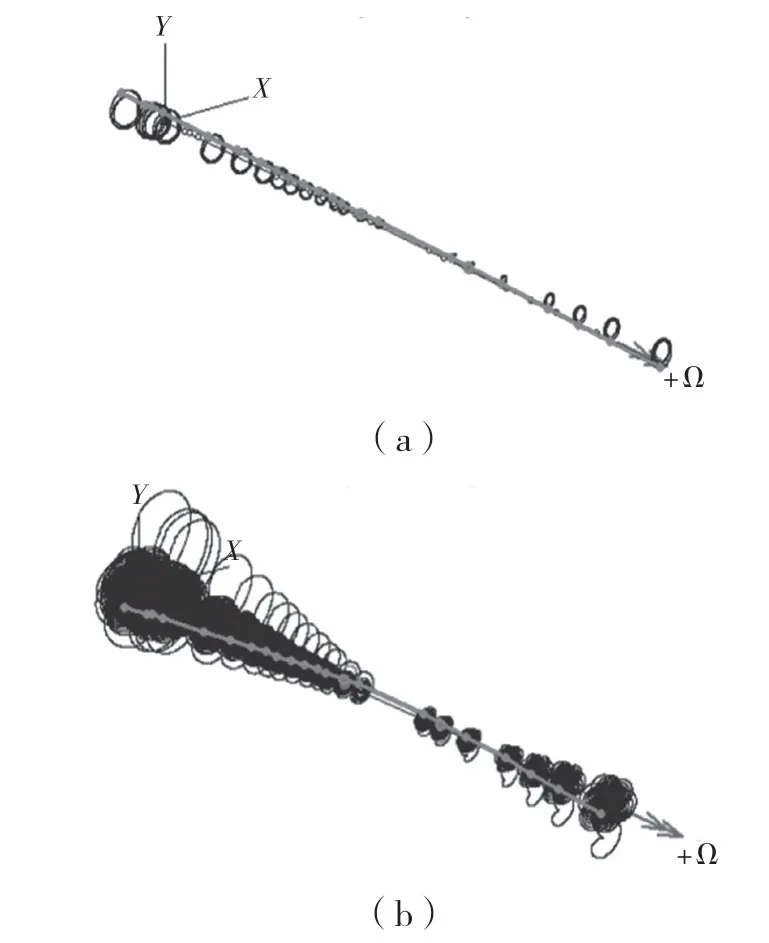
图7 不计入传热影响时转子在10 000 r/min和150 000 r/min 下的运动轨迹Fig.7 Rotor's motion trajectory under 10 000 r/min and 150 000 r/min with influence of heat transfer not taken into account

3 试验台搭建及测试分析结果

3.1 试验台的搭建

选取匹配某款1.0 L 发动机的车用涡轮增压器，在多功能气动试验台架上分别开展升速试验、热吹试验。本研究中的多功能气动试验台架主要用来探究涡轮增压器转子的振动响应并采集数据，试验所用高速动平衡机及多功能气动试验台如图8 所示。

图8 试验台架实物图Fig.8 Physical drawing of test bench

3.2 升速试验

升速试验用来研究涡轮增压器转子动力学性能[8]。图9 展示了涡轮增压器转子在20 000～200 000 r/min 内的涡轮增压器转子压端螺母的振动加速度曲线和仿真中涡轮增压器转子压端螺母的振动位移图。从图中可以总结出两点结论：首先，随着转子转速的上升，试验中转子振动加速度和仿真中转子的振动位移达到最大峰值，即振动强度最大时对应的转速几乎一致，分别为81 200 r/min 和82 360 r/min，误差仅为1.43%；其次，试验中的转子振动加速度和仿真中转子的振动位移变化趋势保持一致。

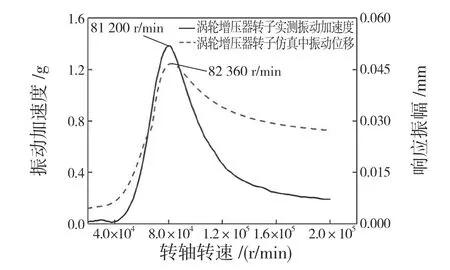
图9 涡轮增压器转子有限元模型标定Fig.9 Calibration of finite element model of turbocharger rotor

3.3 热吹试验

热吹实验用来进一步研究增压器传热对涡轮增压器转子动力学的影响。图10 为涡轮增压器转子压端螺母处在各转速下振动FFT 图的试验值与仿真值的对比情况。

图10 涡轮增压器转子压端螺母振动FFT 图试验值与仿真值对比Fig.10 Comparison between experimental and simulated values of vibration FFT diagram of turbocharger rotor end nut

从图10 中可以发现，转子同步振动响应的试验值和仿真值的误差非常小，这是因为仿真中施加的虚拟不平衡是依据试验数据设置的；油膜力非线性特性引起的次同步振动试验值与仿真值均出现在0.1X 频附近，此时振动振幅试验值与仿真值非常接近。其中存在的一定误差主要是因为实际转子中发生的次同步振动下的原因是多种多样的，并且目前涡轮增压器转子动力学中的非线性问题往往难以精确求解[17]。

综上所述，试验中测得的数据与理论模型计算的结果已经非常接近，从而可以验证本文中搭建的计入涡轮轴—浮环轴承—轴承座传热影响的涡轮增压器转子-轴承系统有限元模型的正确性，能够达到计算分析的要求。

4 结论

本文以某款涡轮增压器转子动态特性为研究对象，对浮环轴承润滑和传热性能进行计算和动力学分析，验证模型的正确性，本文的主要研究内容和结论如下：

（1）详细阐述了涡轮增压器浮环轴承润滑模型和涡轮增压器轴承体及浮环轴承传热理论模型，在此基础上，搭建了计入涡轮轴—浮环轴承—轴承座传热影响下的涡轮增压器转子动力学有限元模型。

（2）对涡轮增压器的浮环轴承动力性分析结果表明，通过各结点处的振动同步响应曲线以及转子在两种不同转速时的运动轨迹，可以看出计入热影响时，各个观测结点位置的最大不平衡响应振幅和转轴转速以及高转速下的振动响应均大于不计入传热影响时。

（3）基于高速动平衡机和多功能气动试验台架开展涡轮增压器转子动力学试验研究。升速试验、热吹试验结果表明，在考虑传热和润滑的情况下，由浮环轴承支承的转子能够稳定运行，且其动力性较好。