基于电感特征的并联电抗器匝间短路故障识别方法

陈继瑞，李宝伟，2，倪传坤，石 欣，王东兴，吕利娟

（1. 许继集团有限公司，河南省许昌市 461000；2. 强电磁工程与新技术国家重点实验室（华中科技大学），湖北省武汉市 430074）

0 引言

高压并联电抗器（简称“高抗”）是一种铁芯带气隙的大容量并联电感线圈［1］，在结构上与变压器绕组有所不同，不易发生励磁涌流。但当高抗空充或与线路容抗产生低频振荡时，高抗铁芯在低频分量长时间的励磁作用下，有可能导致高抗绕组铁芯出现饱和的现象。

近年来，由于电抗器发生饱和，导致匝间保护误动的案例时有发生。文献［1］分析了一起高抗匝间保护误动事故，在线路区外故障切除后，高抗相电流中叠加了高比例的低频分量，导致高抗出现了饱和，匝间保护出现误动作。文献［2-3］分析了高抗-串补线路在两侧断路器断开时的零输入响应，并针对串补的不同补偿度仿真了高抗中性点小电抗电流。结果显示，高抗在上述低频分量的影响下，小电抗电流最大可达到额定电流的3～5 倍，从而将导致高抗饱和［2-3］。可见，在低频分量作用下，高抗也会出现饱和，特征与匝间故障相似，不易区分。但匝间短路故障及绕组铁芯饱和，实质上都是绕组电感特征发生了变化。因此，在研究匝间短路故障识别过程中高抗绕组电感参数的计算有十分重要意义。

文献［1］给出了一种以高抗绕组电抗值波动特征来表征电感变化的方法。该方法计算电抗时基于全周傅里叶算法，需要1 个工频周期的数据。低频振荡时由于频率不能实时测量，这将增加电感值计算误差。高抗由于线圈电感值比较大，当发生少数匝间短路故障时，仍可以长期运行，对速动性要求不高。因此，随着微机保护的发展，出现了实时性相对较低且基于多源数据分析的小波分析法、神经网络分析法等方法［4-9］，力求实现故障与饱和的准确区分。但轻微的匝间短路仍会持续损害绕组，可能发展成更严重的短路故障，所以速动性仍是必要的。

本文通过分析高抗绕组的拓扑模型，通过自互感理论，推导高抗回路方程，得出匝间短路时电感与高抗绕组端口电压、电流、短路环流以及线圈内阻之间的映射关系，构建了匝间故障时的高抗回路等效模型，提出了基于最小二乘法的电感值时域计算方法。针对匝间故障识别问题，分析了零序功率方向原理的匝间保护误动的原因以及铁芯饱和的机理；研究了高抗绕组发生匝间短路故障及铁芯饱和时，高抗绕组电感及电感变化率的不同收敛特征；提出了基于电感特征的并联电抗器匝间故障识别方法。最后，通过仿真验证了本文方法的正确性和有效性。

1 电抗器绕组电感值计算方法

高压并联电抗器主设备的常用拓扑和仿真模型如图1 所示。高抗为了提高补偿度，往往绕组内都带有铁芯，其结构类似于空载变压器源边中性点接地绕组，不同之处在于电抗器绕组铁芯带有气隙，可以有效抑制铁芯饱和及励磁涌流产生［10-16］。因此，正常情况下，可以根据电磁变换原理，列出端口电压方程，求出高抗绕组电感［17-20］。

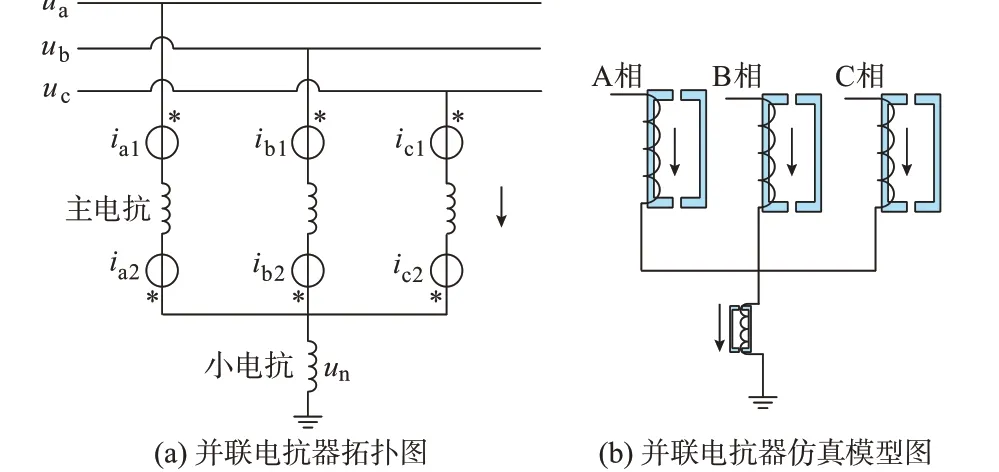
图1 并联电抗器拓扑模型图Fig.1 Topology model diagram of shunt reactor

图1 中:ua、ub、uc分别为并联电抗器首端端口三相电压；ia1、ib1、ic1分别为并联电抗器首端三相电流；ia2、ib2、ic2分别为并联电抗器未端三相 电流；un为中性点电抗端口电压，无中性点电抗器（小电抗）时un=0；蓝色部分表示带气隙的铁芯，对模型进行等效变换后，列出匝间短路等效电路图，如图2 所示。

图2 并联电抗器匝间短路故障等效电路图Fig.2 Equivalent circuit diagram of inter-turn short-circuit fault of shunt reactor

图2 中:RW、RD分别为未短路绕组、短路绕组的线圈内阻；LW、LD分别为未短路绕组、短路绕组的电感；LZ为电抗器未短路时绕组的总电感，LZ=LW+LD；M为未短路绕组与短路绕组之间的互感；i0为中性点电抗流过的电流；iD为短路绕组相电流；iφ1、iφ2分别为并联电抗器首、末端φ相电流，φ=a，b，c。

依据自互感理论，列出未短路绕组相电压、相电流、短路电流、内阻及短路绕组电感之间的回路方程:

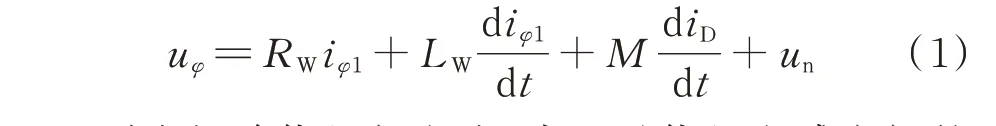
列出短路绕组相电流、内阻及绕组电感之间的回路方程:

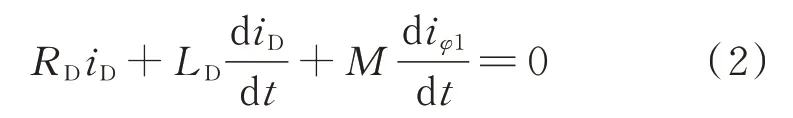
列出中性点电抗绕组电压、电流及绕组电感之间的回路方程:

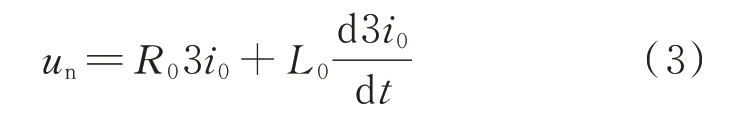
式中:3i0=-(ia2+ib2+ic2)；L0为中性点电抗电感，可由中性点电抗额定值ZL0计算得到，即ZL0=ωL0，ω为工频角频率；R0为中性点电抗内阻。

若并联电抗器带有中性点电抗时，联立式（1）至式（3），得到端口电压方程式（4）和考虑了短路绕组互感影响的测量替代变量Rc、Lc间的映射关系式（5）。

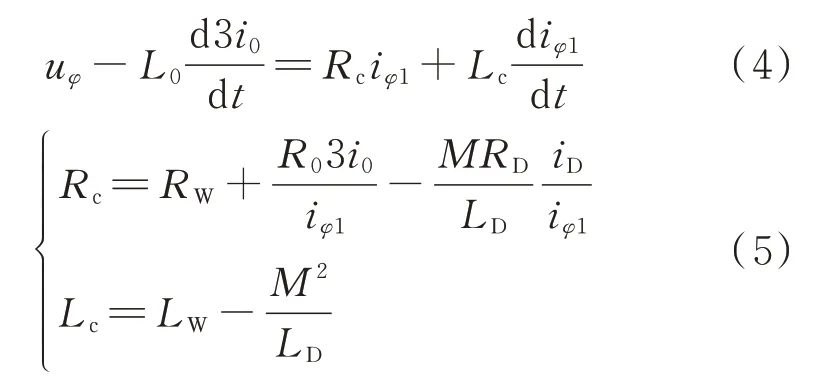
当匝间短路发生时，匝间短路绕组自感LD、互感M、中性点电抗电流3i0和主电抗绕组电流iφ1均是确定值。因此，匝间短路工况下计算出的Rc、Lc也是确定值。从而，将式（4）离散化后，利用最小二乘法即可求得最优解。

将式（4）离散化后得到:

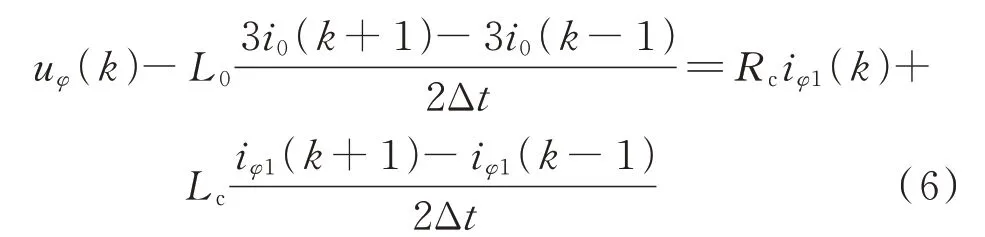
式中:k为计算样本序列；Δt为计算样本采样间隔时间。

由式（5）可知，通过式（6）计算出的匝间故障时电感Lc要比实际绕组电感LW小，这是因为发生匝间短路时，受短路绕组与未短路绕组间的互感影响所致。将LZ=LW+LD代入式（5）可得:

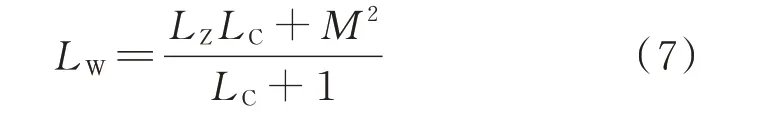
由图2 和式（7）可知，主电抗绕组发生短路故障被分割成多个电感回路时，才会引入互感影响。由于互感未知，可以使用求解的替代变量Lc进行匝间故障识别。在整定匝间故障识别电感阈值时，考虑到可靠性要求，可以将阈值整定的相对低一些。

2 电抗器电感值及其变化率分析

第1 章分析介绍了高抗绕组电感的计算方法，但仅通过电感值大小来识别绕组是否发生匝间故障还是不够的。因为在电抗器饱和工况下，绕组电感值也会变小，这与匝间故障特征相似。因此，在识别匝间故障可靠动作时，还要考虑高抗饱和工况下，系统扰动不能误动作。

2019 年，某220 kV 电压等级海上风电场变电站线路送电合开关时，线路高抗的匝间保护150 ms 后出现误动作，导致送电失败。现场高抗主接线拓扑如图3 所示，包含风力发电机、升压变压器、海缆输电线路、并联电抗器、负载及大电网系统。现场匝间保护误动波形如附录A 图A1 所示。现场误动波形中的相电流、零序电压及零序电流量的故障特征，如附录A 图A2 所示。

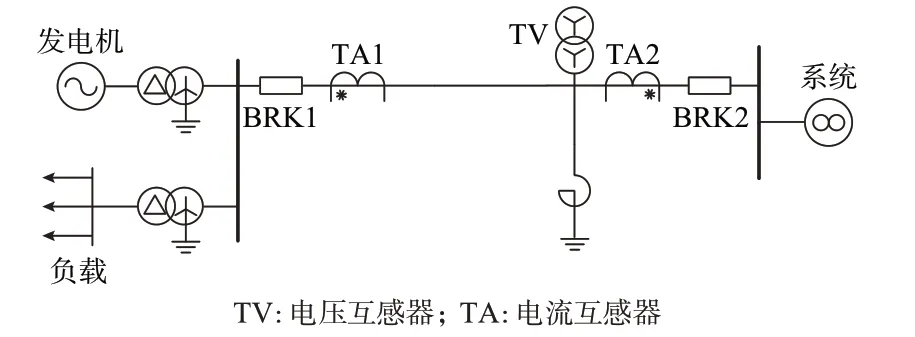
图3 并联电抗器主接线拓扑Fig.3 Main wiring topology of shunt reactor

现场高抗匝间保护动作原理概括如下:采用传统零序功率方向识别故障原理作为主判据，配合电抗器零序电压、零序电流、零序测量阻抗及相电流二次谐波判据等辅助判据，综合识别匝间故障。因此，结合附录A 图A1 和图A2 中的波形特征，得出引起并联电抗器匝间保护误动作的原因，分析如下。

1）满足零序功率方向元件识别判据。传统匝间保护识别原理为零序电压、电流功率方向判别，电抗器内部故障时，零序电流的相位超前零序电压接近90°；电抗器外部单相接地短路故障时，零序电流的相位则滞后零序电压；由图A1 波形数据可计算出零序电流相位超前零序电压120°左右，满足零序功率方向识别判据。

2）满足零序阻抗元件识别判据。电抗器的一次零序阻抗一般为几千欧姆，而系统一次零序阻抗通常为几十欧姆，从而可以通过测量电抗器端口零序阻抗，判断是否发生匝间故障。由图A1 可知，保护启动约20 ms 后，零序测量阻约为19 Ω，远小于高抗额定二次零序阻抗的25%，高抗额定二次零序阻抗为175 Ω。

3）满足零序电流、零序电压阈值识别判据。图A2 中，匝间保护零序电压最小值约为0.67 V，大于动作阈值0.5 V。零序电流也大于阈值0.04 A。

4）满足相电流谐波识别判据。图A2 中，三相电流中二次谐波含量特征:A 相和B 相含量均在15%～6%范围内，并呈现递减趋势。C 相含量几乎为0，满足二次谐波识别匝间故障元件判别。图A2（a）中，A 和B 相电流中的直流分量都比较大，均在40%以上。

由以上分析可知，并联电抗器匝间保护故障识别的零序功率方向、零序阻抗、相电流二次谐波、零序电压以及零序电流等判据条件满足，匝间保护出现误动作。由附录A 图A2 所示现场波形故障特征分析可知，电抗器铁芯出现饱和特征，与匝间故障相似，难以区分，最终导致匝间保护误动作。

综上所述，现有电抗器匝间保护无法可靠识别高抗饱和现象。当存在外部扰动时容易发生误动作，亟须提出一种新的应对高抗饱和的匝间保护故障识别方法。

2.1 基于电感特征的匝间故障识别方法

由文献［1］分析结论可知，低频谐振分量也是引起带铁芯并联电抗器饱和的因素之一。对于图3 所示海上风电场电缆送出线路，海缆对地电容与并联电抗器之间的谐振也不能忽视。按国内线路通常无功补偿度为40%～50%考虑，例如BRK1 开关分位、BRK2 开关由合到分时，海缆电容和电抗设备间将会产生LC 谐振，由式（8）可计算出，系统振荡频率为33 Hz 左右，低于工频频率。

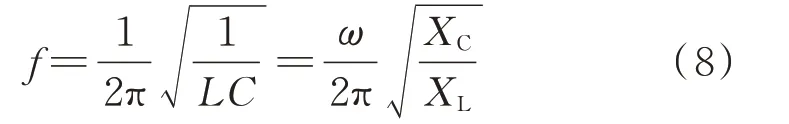
式中:L为系统电感；C为系统电容；XC为线路容抗；XL为电抗器感抗。

本文为了深入研究电抗器绕组阻抗值在电抗器空充、匝间故障及低频谐振时的变化特征，消除非周期暂态分量和系统非工频工况的影响，提出了利用主电抗器绕组测量电感Lc与额定电感Le之间的关系特征，以及测量电感变化率LΔ的特征关系，来替代分析绕组阻抗的变化特征，电感变化率方程如式（9）所示。

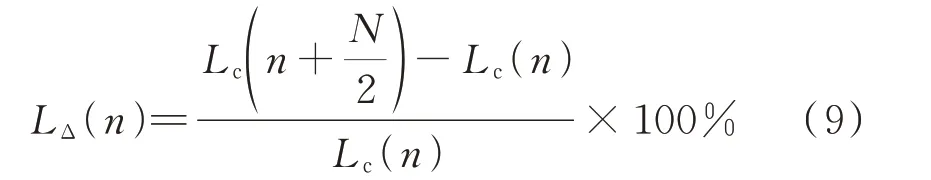
式中:Lc(n)为使用本文方法计算出的电感样本值；N为最小二乘法数据窗样本个数；n为样本序列。

因此，本文针对电抗器空充、LC 振荡以及匝间故障3 类工况，利用MATLAB 和实时数字仿真（RTDS）研究电抗器绕组的测量电感和电感变化之间的特征。电抗器参数如下:三相容量为55 Mvar，额定电压为230 kV，50 Hz 工频下的额定电感值为1.148 H。

2.2 电抗器空充时电感及其变化率分析

当电抗器进行空充和空充于B 相绕组7%匝间故障时，电抗器三相电感及电感变化率的仿真结果如附录A 图A3 所示。

由附录A 图A3（a）可知，在电抗器空充饱和时，饱和相电感值陡然变小，然后随着饱和消退，逐渐收敛于额定电感附近；电感变化率剧烈变化，逐渐收敛趋近于0，呈现稳态特征。

由附录A 图A3（b）仿真结果可知，在电抗器空充B 相7% 匝间故障时，B 相故障绕组电感计算值为0.409 H，电抗器电感值陡然降到额定值的50%以下，并收敛于该稳定值。电感变化率快速收敛趋近于0，呈现稳态特征。

2.3 电抗器谐振时电感及其变化率分析

当线路两侧开关由合到分、电抗器与线路发生LC 谐振时，电抗器三相电感及电感变化率仿真结果如附录A 图A4 所示。由图A4 分析可知，电抗器电压取线路电压互感器谐振时，电抗器电感值随着谐振能量的衰减，由某一小值逐渐收敛于额定电感附近；电感变化率剧烈变化，逐渐收敛趋近于0，呈现稳态特征。

对于线路电抗器电压取母线电压互感器的特殊工况，GB/T 14285—2020 标准中明确规定了“对于线路高压并联电抗器，匝间保护应使用并联电抗器所在线路间隔的三相电压互感器”，因此，不再展开分析。

2.4 电抗器匝间故障时电感及其变化率分析

当电抗器发生A 相3% 和5% 典型匝间故障时，电抗器三相电感及电感变化率仿真结果如附录A 图A5 所示。由图A5 仿真结果可知，发生A 相3% 和5% 匝间故障时，电感分别为0.657 6 H 和0.504 8 H。电抗器故障相电感值均快速下降到额定值的50%以下，并收敛于该稳定值。电感变化率快速收敛趋近于0，呈现稳态特征。

2.5 电感特征分析总结

由2.2～2.4 节中电抗器绕组电感值及其变化率的研究分析可知，电抗器绕组在发生空充饱和、匝间故障及低频谐振时，绕组电感值均小于额定电感值。因此，仅通过电感值的变化特征无法直接识别出匝间故障工况。

从附录A 图A3 至图A5 所示电抗器绕组电感变化率的特征可知:1）当电抗器空充时，饱和相绕组电感变化率经过约800 ms 大幅振荡后，收敛于0；2）电抗器空充匝间故障时，故障相电感变化率经小幅振荡后，快速收敛于0；3）电抗器低频谐振时，谐振相电感变化率经过约300 ms 大幅振荡后，收敛于0；4）电抗器正常运行发生3%～5%匝间故障时，故障相电感变化率经过约40 ms 振荡后，快速收敛于0。

综上，通过识别出电感值小于某一额定电感值且经短时间确认电感变化率均小于某一阈值时，就可以认为识别出发生了匝间故障；否则，认为未识别出匝间故障。

2.6 谐波辅助识别判据

电抗器绕组铁芯中带有大量气隙，往往可以起到有效抑制涌流的作用。在某些特殊的运行工况下，当电抗器由于外部干扰或自身结构的原因而发生铁芯饱和时，绕组相电流的饱和识别特征将会变得不再明显，如附录A 图A2 所示现场误动波形中，相电流二次谐波含量出现低于经验值15%的工况。

另外，电抗器三相绕组相电流中含有基波有效值为相额定电流的负荷电流，这将进一步降低相电流中的谐波含量，导致谐波含量不明显。

空充电抗器与变压器类似，受合闸角影响，三相铁芯不会同时出现严重饱和，往往至少有一相饱和特征不明显。因此，非对称饱和将会引起零序电流出现。

考虑到空充电抗器饱和特征的抑制性，结合以往的涌流识别经验，采用零序电流中的二、三次谐波含量及电感特征满足相的电流有效值一起进行饱和识别，提高绕组铁芯饱和识别的可靠性。

由上述分析可知，增加零序电流二、三次综合谐波小于阈值门槛或电感特征满足相电流阈值时的开放条件。零序电流综合谐波计算如式（10）所示；现场空充误动波形的二、三次综合谐波含量，如附录A图A6 所示。

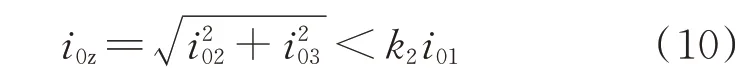
式中:i0z为零序电流综合谐波；k2为零序电流综合谐波系数；i01、i02、i03分别为零序电流的基波、二次谐波和三次谐波。

由附录A 图A6 可以看出，零序电流综合谐波含量均在20%以上，且最小值为21%。若单独使用零序电流中的二次谐波或三次谐波含量来识别铁芯饱和，可能会降低可靠性。

对电抗器发生A 相3%和5%典型匝间故障时相电流有效值关系进行分析，电抗器绕组额定电流Ie为0.16 A，结果 如附录A 图A7 所示。由图A7 可知，电抗器发生A 相3%匝间故障时，故障电流约为1.73Ie；电抗器发生A 相5%匝间故障时，故障电流约为2.24Ie。结合图A1 所示现场误动空投波形，最大相电流约为1.37Ie。因此，电抗器相电流有效值对于饱和与匝间故障识别也具有明显特征。

综上，只要对测量电感Lc和电感变化率LΔ设置合理的条件约束，配合零序电流综合谐波判据和电感特征满足相电流特征，考虑一定延时裕度，延时取50 ms，满足确认条件后，就可以准确识别出匝间故障，快速开放匝间保护。基于电感特征的匝间故障识别判别逻辑如图4 所示。

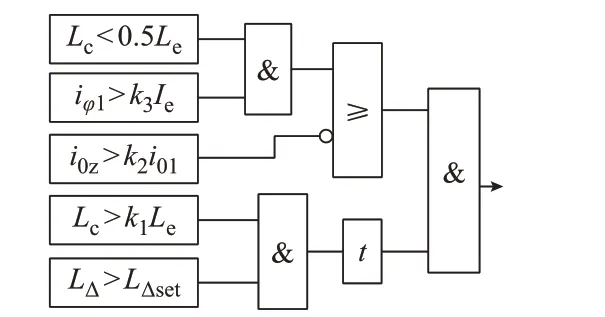
图4 匝间故障识别判据逻辑图Fig.4 Logic diagram of inter-turn fault identification criteria

图4 中:k1为约束电感系数；k3为相电流系数；LΔset为约束电感变化率阈值。图中判据参数的整定原则如下:1）考虑5%以上匝间故障保护可靠动作，3%匝间故障保护也有足够的灵敏度，k1按不小于额定电感值的70%整定；2）考虑5%以上匝间故障保护可靠动作，3%匝间故障保护也有足够的灵敏度，LΔset按不小于1.15%整定；3）k2整定值不大于20%即可，考虑可靠性，可按经验值取15%；4）考虑5%以上匝间故障保护可靠动作时k3可按不大于2 整定，考虑3%匝间故障保护有足够灵敏度时k3可按不大于1.5 整定；5）匝间故障保护的灵敏性和速动性不可兼得。因此，当相电流增加到大于2 倍或1.5倍额定电流（为保证可靠性建议按2 倍整定）且测量电感小于额定电感值的50%时，不再判别谐波，仅判别电感特征满足判据即出口。

2.7 仿真和动模验证

以220 kV 电压等级某输电线路电抗器参数为例，线路补偿度按45%整定，进行RTDS 建模仿真分析，验证基于电感特征的电抗器匝间保护的性能，电抗器模型参数如附录A 表A1 所示，工频50 Hz时，主电抗器额定电感为1.148 H。

为了验证本文中电抗器绕组电感模型及求解电感值的正确性，在电抗器正常运行工况下，分别利用本文算法和全周傅里叶算法，计算出电抗器绕组的电感值，进行对比验证，如附录A 图A8 所示。结果显示，本文算法计算出的电感值比全周傅里叶算法更逼近额定电感值1.148 H，这是因为本文算法在建模时考虑了电感线圈内阻的影响，验证了本文算法的正确性。

另外，针对高压并联电抗器模拟空投、空投匝间故障、线路开关分闸谐振以及正常运行发生典型5%匝间故障等工况，分别进行了多次动模试验。试验总结发现，在k1取值为0.7、LΔset取值为1.15%、k2取值为15%、k3取值为2 时，匝间保护均能可靠识别出故障。

并联电抗器发生谐振及饱和工况下，匝间保护均能可靠不动作。实验结果见附录A 图A9 至图A11，验证了基于电感特征的匝间故障识别方法的有效性。

另外，对附录A 图A3 中电抗器空充于B 相绕组7%匝间故障时零序电流综合谐波与相电流特征进行仿真，结果如图5 所示。

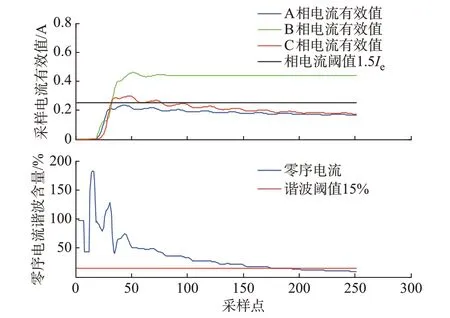
图5 电抗器空充故障时的零序电流特征Fig.5 Zero-sequence current characteristic of reactor during no-load charging fault

由图5 中可以看出，当空充于B 相7%匝间故障时，零序电流的综合谐波含量较高，直到170 ms 左右衰减到15%。但是B 相电流有效值在30 ms 处即达到了相电流阈值，匝间保护可以可靠开放，验证了相电流开放逻辑的正确性。

3 结语

分析了高抗绕组拓扑和仿真模型，构建了高抗绕组匝间故障的等效电路模型。通过自互感方程，推导出绕组电感与电抗器绕组端口电压、电流、短路环流、线圈内阻及中性点电抗之间的映射关系，提出了基于最小二乘法的电感值时域计算方法。

分析了传统零序功率方向原理的匝间保护在铁芯饱和时误动的原因以及铁芯饱和的机理。研究了高抗绕组发生匝间短路故障及铁芯饱和工况时，电抗器绕组电感值及电感变化率的收敛特征，提出了基于电感特征的并联电抗器匝间故障识别方法，并配合零序电流综合谐波及绕组相电流特征共同识别电抗器铁芯饱和。通过与全周傅里叶算法电感值计算结果进行对比，验证了本文方法的正确性。通过RTDS 仿真试验验证了方法在识别电抗器饱和工况时的安全性以及识别匝间故障工况时的可靠性。

本文方法不改变现有匝间保护原理，需在原有匝间保护故障识别判据与新方法故障识别判据同时满足情况下，才会开放匝间保护；当原有匝间保护故障识别判据不满足时，不再判别新方法判据，直接闭锁匝间保护。本文方法既提升了原有匝间保护原理的故障识别能力，又不降低原有匝间保护原理的可靠性，适用性强，有助于提升匝间保护的性能。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。