光伏电站高比例异常运行数据组合识别方法
2022-10-31崔宝丹赵永宁
叶 林,崔宝丹,李 卓,赵永宁,路 朋
(中国农业大学信息与电气工程学院,北京市 100083)
0 引言
截至2020 年底,中国累计光伏装机总容量已达到253 GW[1]。预计在“碳达峰·碳中和”背景下,光伏装机容量会持续大幅攀升。随着光伏装机容量的快速增长和光伏发电系统的智能化运行,光伏电站运行数据的研究已成为该领域研究的热门课题[2-3]。其中,准确、可信的光伏功率数据是光伏发电性能评估[4]、光伏功率预测[5]及光伏并网[6-7]等研究的基础。然而,由于设备故障、消纳能力有限等原因,许多光伏电站现场采集的功率数据中含有大量的异常数据,这不仅影响了光伏功率数据本身的数据质量,而且大大降低了相关实验和测试结果的准确性。因此,开展光伏功率高比例异常数据识别方法研究具有重要意义。
异常数据识别是各类数据分析的重要环节,现有的异常数据识别方法可分为单体异常数据识别方法和组合异常数据识别方法两类。单体异常数据识别方法中的常见方法包括基于统计指标[8-9]、聚类分析[10-11]以及回归分析[12]等方法;组合异常数据识别方法是采用多个单体方法分别识别不同类型的异常数据。这两类异常数据识别方法在风电功率异常数据识别[13-14]、负荷异常数据识别[15]及一次设备状态监测异常数据识别[16]等领域均有一定的应用。相关研究表明,组合异常数据识别方法相比于单体方法识别效果更好[17-19]。
随着光伏装机规模的增大,越来越多的学者开始研究光伏发电中的异常数据问题。文献[20]依据中心极限定理,将光伏功率数据分布视为正态分布,采用3-Sigma 方法对光伏功率异常数据进行识别。但已有研究表明,只有在晴天时光伏功率数据才接近正态分布[21],且高比例异常数据也会使光伏功率数据的分布发生变化,导致采用该方法进行异常数据识别效果不佳。文献[22-23]分别在仅考虑辐照度和考虑多种影响因素的情况下,通过Copula理论函数构建辐照度与光伏功率之间的概率曲线,实现光伏功率异常数据的识别。然而,大量的异常数据将会使Copula 分布参数发生畸形,从而影响异常数据识别的准确性。文献[24]提出利用异常数据和正常数据分界处滑动标准差突变的特点进行光伏功率异常数据识别的方法,但正常数据和异常数据间分界不明显的高比例异常数据会导致滑动标准差变化不明显,从而影响滑差阈值的选取和异常数据的识别效果。
由上述研究可知,目前的光伏功率异常数据识别方法仍具有一定的局限性。一方面,现有光伏功率异常数据识别方法受异常数据占比的影响显著,在正常数据和异常数据界限不明显的光伏功率高比例异常数据条件下,大部分光伏功率异常数据难以被有效识别;另一方面,现有文献大多采用单体方法进行异常数据的识别,忽略了组合方法对不同单体方法识别优势的整合,故在某些特殊异常数据条件下识别效果欠佳,且通用性较差。
基于上述分析,本文提出了一种适用于光伏功率连续型和离散型异常数据的组合识别方法。在对光伏功率数据进行相似日划分的基础上,首先,利用本文所提同时段均值对比算法对连续型异常数据进行识别,剔除高比例的连续型异常数据后,再采用四分位法对少量的离散型异常数据进行识别。同时,通过对比异常数据识别前后辐照度和光伏功率的线性相关程度,实现不同相似日聚类下同时段均值对比算法最优参数的选取和异常数据识别效果的评估。最后,将本文方法分别与四分位法[25]和3-Sigma 方法[26]进行对比,证明了本文所提组合异常数据识别方法在光伏功率高比例异常数据识别中的有效性。
1 光伏异常数据特征及高比例异常数据定义
1.1 异常数据分类
光伏功率受气象因素影响较大,且在各种气象因素中,受太阳辐照度影响最大[27]。在正常情况下,光伏功率数据与太阳辐照度基本呈线性正相关关系[28]。而在实际运行情况下,设备故障、通信故障、弃光限电及机组停机等事件的发生均会产生大量的异常功率数据。其中,大部分异常功率数据的主要特征是在连续一段时间内,光伏功率持续偏低,甚至功率数据持续为0,此种异常数据多由光伏限电、设备故障等在较长时间内难以恢复正常的情况导致。此外,少量异常数据是由通信短时异常导致光伏功率记录数据突变产生的,其通常具有较快恢复正常的特点[10]。本文将上述两种特征的光伏功率异常数据定义为连续型异常数据和离散型异常数据。标记典型连续型异常数据和离散型异常数据如图1 所示。
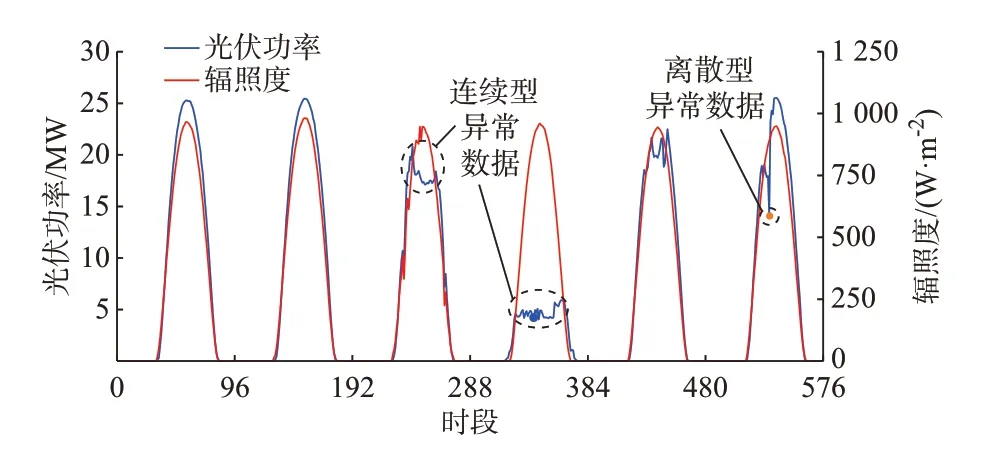
图1 相似辐照度下光伏功率时序示意图Fig.1 Schematic diagram of photovoltaic power time sequence under similar radiation
1.2 高比例异常数据定义
正常光伏功率数据和辐照度间呈线性正相关关系,但是随着异常数据占比的增大,两者间的线性相关程度会随之减小。本文利用皮尔逊相关系数计算方法来表征辐照度和光伏功率的线性相关程度[29]。线性相关程度r的计算公式如式(1)所示。

式中:Ri和Pi分别为辐照度大小和光伏功率大小;Rˉ和Pˉ分别为辐照度均值和光伏功率均值;m为辐照度-光伏功率数据对的数量。
本文实验所用3 个光伏电站的原始辐照度-光伏功率线性相关程度分别为87.78%、92.73% 和84.13%,与其他两个线性相关程度较低的光伏电站相比,利用四分位法和本文所提方法对线性相关程度为92.73%的光伏电站异常数据识别后线性相关程度提高相差较小。基于此先验知识,本文将辐照度和光伏功率线性相关程度小于90%的数据定义为含高比例异常数据的光伏功率数据。图2 分别展示了含低比例异常数据和高比例异常数据的辐照度-光伏功率散点图,两个光伏电站的辐照度和光伏功率线性相关程度分别为94.99%和87.78%。
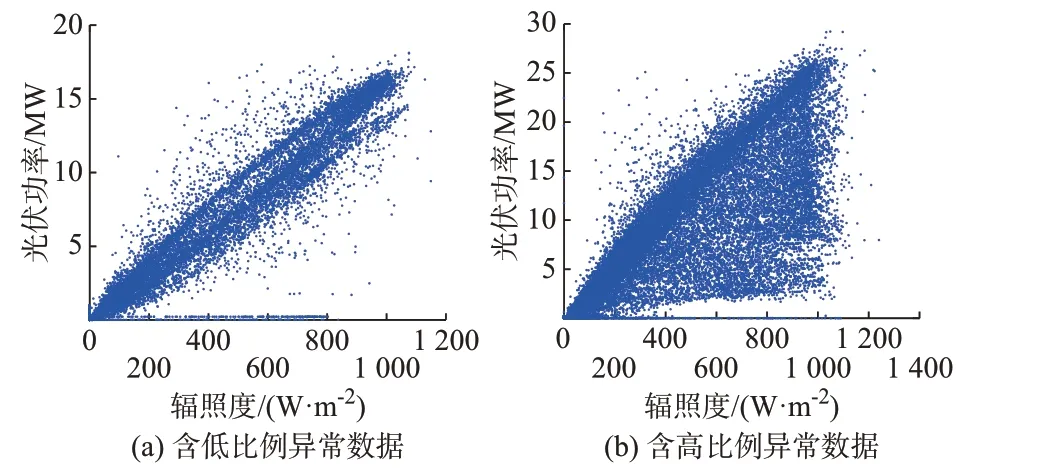
图2 含典型比例异常数据的光伏电站辐照度-光伏功率散点图Fig.2 Radiation-photovoltaic power scatter plots of photovoltaic power station with typical ratio of abnormal data
2 异常数据识别原理和总体识别框架
2.1 相似日划分
2.1.1k均值聚类算法
k均值聚类算法可实现大型数据集聚类,因其所得结果簇比较紧凑,各个簇之间可以实现明显的分离,故本文选取该聚类算法进行相似日划分。又因为k均值聚类算法是目前各种研究中常用且原理简单的聚类算法之一,故本文对该算法原理不作具体阐述,其具体使用方法见文献[17]。在相似日划分前,利用式(2)对辐照度数据进行归一化处理。

2.1.2 聚类个数确定方法
k均值聚类算法中,聚类个数k值大小对相似日划分的准确性会产生较大影响,因此,需在相似日划分前进行相似日聚类数目的确定。作为一种常用的聚类数目确定方法,手肘分析法通过对比不同聚类数目下聚类的损失函数下降程度来确定聚类数目。绘制不同聚类数目下聚类损失函数值的折线图,定义聚类损失函数值E在骤降和缓慢下降的转折点对应的k值为数据集的最佳聚类数目[30]。
为了定量确定最佳聚类数目,分析多个光伏电站在不同聚类数目下的损失函数变化情况,得到聚类数目确定方法如式(3)所示。

式中:Ea表示聚类数目为a时,聚类结果的损失函数值;ΔEa为从聚类数a-1 到聚类数a时损失函数值的下降数值;ΔÊa为从聚类数a-2 到a存在的两个损失函数下降数值的差值;kbest为选取的最优聚类个数;(ΔÊc)first<0.1 表示根据损失函数下降数值的差值第1 次小于0.1 时的聚类数c,可以得到最优聚类个数kbest。
2.2 组合异常数据识别方法
连续型异常数据大多由光伏电站主动弃光和机组停机产生,因此,连续型异常数据与正常数据相比,多是在相同辐照度下具有较低的光伏功率。又因为连续型异常数据在时间上具有连续性,提出通过对比相似辐照度下光伏功率均值大小的方法实现连续型异常数据的识别,并将该方法称为同时段均值对比算法。大部分异常数据在连续型异常数据识别阶段被剔除后,再利用四分位法对剩余少量离散型异常数据进行识别。本文对光伏功率数据采用实际光伏功率数据除以额定装机容量得到光伏功率标幺值的方法进行了归一化处理。
2.2.1 同时段均值对比算法
理论上,在相同辐照度下,光伏有功功率数据应基本相同,即在日辐照度相近的相似日聚类下,各时段的光伏功率数据应大小相近。所提方法采用各时段光伏功率均值作为相似日聚类下,各时段光伏功率数据相近性的表征指标。
以某相似日为例,同时段均值对比算法进行连续型异常数据的识别过程如下:历史光伏功率数据的采样频率为15 min,即每天的光伏功率数据包括96 个数据点。设该相似日聚类下包含的数据天数为n,则该相似日聚类和相似日聚类下某日包含的光伏功率数据可分别表示为式(4)和式(5)。
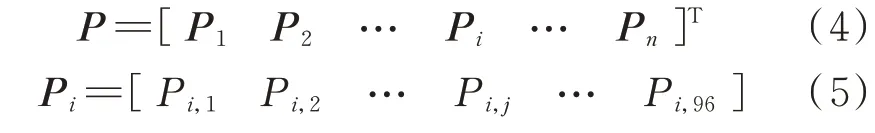
式 中:Pi,j为 第i天 第j个 时 段 的 光 伏 功 率 数 据;Pi为第i天的光伏功率数据;P为相似日聚类下n天的光伏功率数据。
对相似日聚类下n天的光伏功率数据划分时段。设每个时段包含m个光伏功率数据,则每日光伏功率可被划分为s个功率时段,且满足ms=96。相似日聚类下n天的光伏功率数据中,第j个时段的光伏功率数据可表示为:
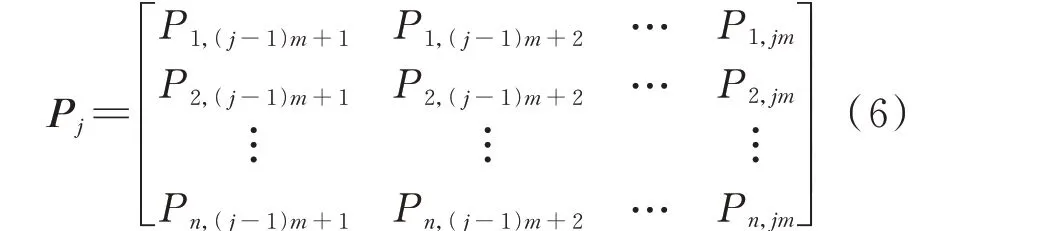
式 中:Pi,(j-1)m+1,Pi,(j-1)m+2,…,Pi,jm表 示 第i天 第j个时段各个时间点的光伏功率数据。
对第j个时段的光伏功率数据进行均值计算,得到相似日聚类下n天光伏功率数据中第j个时段的光伏功率均值为:

式中:Pˉi,j为第i天第j个时段的光伏功率均值,i=1,2,…,n。
称第j个时段的光伏功率均值的最大值为相应辐照度下的最大功率均值。在相似辐照度下,受温度、气压等其他气象因素的影响,正常光伏出力数据会存在小于最大功率均值的情况。又因为辐照度是影响光伏功率最重要的因素,故在相似辐照度下,温度、气压等气象因素不会导致光伏功率均值与最大功率均值间存在过大的差距。本文利用相似辐照度下的最大功率均值实现连续型异常数据均值的阈值划分,划分结果表示为:
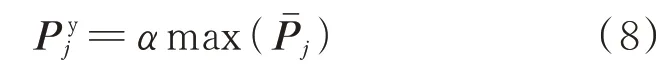
式中:Pyj为某相似日聚类下第j个时段的均值阈值;max(Pˉj)为某相似日聚类下第j个时段的最大功率均值;α表示连续型异常数据均值的阈值与该时段最大功率均值的比值大小,称为连续型异常数据的均值阈值系数。
因为连续型异常数据多由短时间内无法恢复的故障及因电网本身消纳能力不足引起的限电所致,故将光伏功率均值小于同时段均值阈值的光伏功率数据识别为连续型异常数据段。为了避免不同季节下,光伏起始出力和结束出力时间点的不同导致正常未出力光伏功率数据被误识别为连续型异常数据,依据光伏电站在一年中的最晚起始出力和最早终止出力时间,选取进行连续型异常数据识别的时间段,并仅对选取时间段下的光伏功率数据进行连续型异常数据识别。
2.2.2 同时段均值对比算法参数选取
相似日聚类下,功率数据划分的时段大小和阈值系数的选取均会对连续型异常数据的识别效果产生影响。为实现连续型异常数据的高质量识别,采用“定阈值系数,变时段大小”和“定时段大小,变阈值系数”的方法分别实现最优时段大小和最佳阈值系数的选取。“定阈值系数,变时段大小”是通过对比阈值系数固定的情况下,划分不同时段大小进行的连续型异常数据的识别效果,从而实现最优时段大小的选取;“定时段大小,变阈值系数”是通过固定最优时段大小,比较不同阈值系数下连续型异常数据的识别效果。
α值越大,由式(8)可知计算得到的连续型异常数据段的均值阈值越大,小于该均值阈值的数据段数据便会增多,即识别得到的连续型异常数据段越多,保留的正常数据段越少。不同阈值系数选取下,异常数据段均值阈值划分结果如图3 所示。
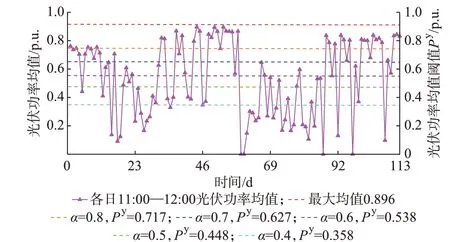
图3 不同阈值系数下的均值阈值划分结果示意图Fig.3 Schematic diagram of division results of mean threshold with different threshold coefficients
阈值系数的选取不仅要考虑最终异常数据识别后整体数据的线性相关程度大小,而且要考虑异常数据剔除率的大小。根据不同阈值系数下的异常数据识别效果分析可知,在各相似日聚类中不同阈值系数下,数据剔除率在高于20%后,辐照度和光伏功率的线性相关程度提高缓慢,甚至在相似日聚类3 中存在线性相关程度下降的结果。因此,本文为了保证在数据剔除率较低的情况下提高辐照度和光伏功率的线性相关程度,选取20%作为数据剔除率的限值。假设相似日聚类划分为k类,考虑到相似辐照度下的光伏功率基本相同,而各相似日聚类下的日辐照度数据在相似中又存在一定的区别,故均值阈值不宜取得过高或过低。本文为观察多个不同阈值系数下异常数据的识别效果变化,取每个相似日聚类下均值阈值系数的取值范围为[0.4,0.8]。设每个相似日聚类进行连续型异常数据识别的阈值分 别 为{α1,α2,…,αk},αi∈[0.4,0.8](i=1,2,…,k),则第i个相似日聚类在阈值系数为αi情况下异常数据识别后的正常数据为P͂αi。定义阈值系数的选取满足下式:
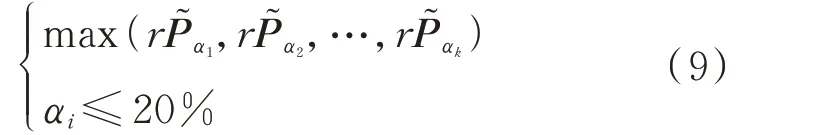
式中:P͂α1,P͂α2,…,P͂αk表示异常数据识别后整体的光伏功率数据;rP͂α1,rP͂α2,…,rP͂αk表示异常数据识别后整体辐照度和光伏功率的线性相关程度,即在满足各相似日聚类数据剔除率均小于20%的情况下,选取使整体数据线性相关程度最大的均值阈值系数。
2.3 异常数据识别总体框架
本文所提组合异常数据识别思路如图4 所示。
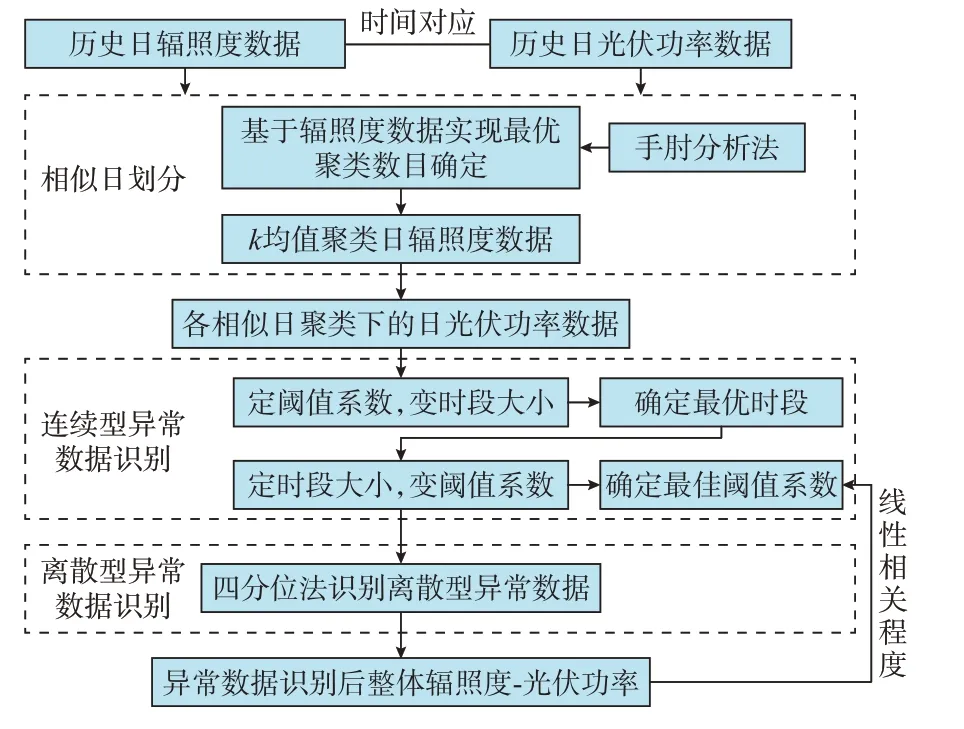
图4 异常数据识别框图Fig.4 Block diagram of abnormal data identification
具体步骤如下:
步骤1:划分相似日聚类。采用k均值聚类对日辐照度数据进行聚类,从而得到相应辐照度下的光伏功率相似日聚类。其中,相似日聚类个数利用手肘分析法进行确定。
步骤2:采用同时段均值对比算法进行连续型异常数据识别,通过“定阈值系数,变时段大小”确定最优时段大小。对不同的相似日聚类分别采用同时段均值对比算法进行连续型异常数据的识别,通过分析相同阈值系数、不同时段大小下连续型异常数据识别后的辐照度和光伏功率的线性相关程度,以及数据剔除率的增长速率确定最优时段大小。
步骤3:采用同时段均值对比算法和四分位法分别进行连续型和离散型异常数据识别,通过“定时段大小,变阈值系数”确定最佳阈值系数。基于步骤2 确定的最优时段大小,分别利用同时段均值对比算法和四分位法实现不同阈值系数下各相似日聚类下连续型和离散型异常数据的识别。通过比较不同阈值系数下两类异常数据识别后的整体辐照度和光伏功率的线性相关程度,实现各个相似日聚类下连续型异常数据识别的最佳阈值系数的选取。
3 算例分析
本文以中国新疆地区3 个光伏电站2017 年1 月2 日至2018 年10 月31 日的实测辐照度数据和光伏功率数据为研究对象,测试本文所提方法对各光伏电站连续型和离散型异常数据的识别和剔除效果。3 个光伏电站的额定装机容量分别为80、30、20 MW。
3.1 模型参数选取及结果分析
根据2.1.2 节中聚类数目的确定方法,得到3 个光伏电站的聚类数目分别为6、7、6。以光伏电站1为例,介绍异常数据识别和剔除过程如下,其原始辐照度-光伏功率散点图如图2(b)所示。
“定阈值系数,变时段大小”阶段,通过固定各时段的光伏功率均值阈值系数α=0.4,将各时段包含的光伏功率数据个数m分别设置为4、8、12,即划分时段大小分别设置为1、2、3 h。观察多个季节光伏电站功率起始出力和终止出力时间,发现光伏电站一年中最晚起始出力时间在08:00—09:00,最早终止出力时间在17:00—18:00。在上述3 种时段大小设置下,对连续型异常数据识别的时段j分别取9~18、5~9 和4~6,并仅对所选时段下的数据进行连续型异常数据识别。得到相似日聚类4 在不同时段大小下,连续型异常数据剔除后的辐照度-光伏功率线性相关程度和数据剔除率如图5 所示,其余5 个相似日聚类的识别效果见附录A。可知在给定阈值系数下,无论各时段大小设置为何值,异常数据剔除后的辐照度和光伏功率的线性相关程度均会提高,且时段大小取值越小,异常数据剔除后的辐照度和光伏功率线性相关程度值越大。当时段大小取1 h 时,异常数据识别效果最好,并且数据剔除率最低。
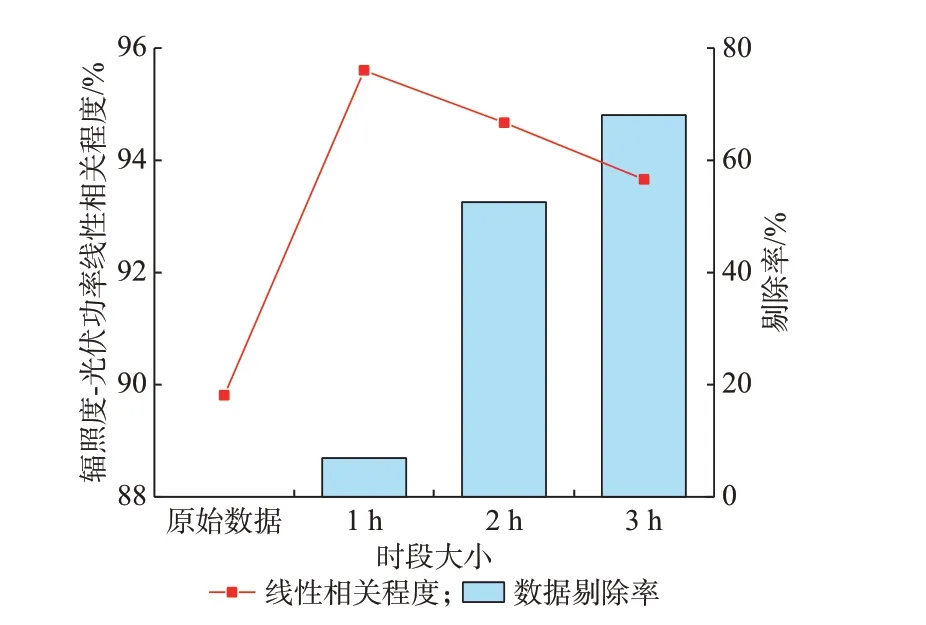
图5 不同时段大小下连续型异常数据识别效果Fig.5 Identification effect of continuous abnormal data with different time periods
基于以上结论,可以得到各相似日聚类下的最优时段大小均应固定为1 h。在“定时段大小,变阈值系数”阶段,固定划分时段大小为1 h,分别设置阈值系数α为0.4、0.5、0.6、0.7、0.8 进行连续型异常数据识别。离散型异常数据剔除过程中,将相似日聚类下的辐照度从小到大进行排序,并将辐照度数据划分成40 个辐照度区间,对每个辐照度区间内对应的功率数据集合采用四分位法[25],剔除功率数据集合中超过四分位上下限的功率数据。对比6 个相似日聚类在不同均值阈值系数下连续型异常数据和离散型异常数据的识别效果,得到相似日聚类4 的异常数据识别效果如图6 所示。其余5 个相似日聚类的识别效果见附录B。

图6 不同阈值系数下异常数据识别效果Fig.6 Identification effect of abnormal data with different threshold coefficients
基于2.2 节中的均值阈值系数确定方法得到光伏电站6 个相似日聚类下的均值阈值系数,分别设置为0.4、0.4、0.4、0.7、0.4、0.6。相似日聚类4 实现异常数据识别前后,辐照度-光伏功率的散点分布及线性拟合直线如图7 所示,其余5 个相似日聚类的识别效果散点分布及线性拟合结果见附录C。相似日聚类4 中,典型连续型异常数据和离散型异常数据识别效果的时序图如图8 所示。由异常数据识别后得到的散点图和时序图可以发现,光伏功率低发在时间上多具有连续性,且在异常数据总量中占比较大。连续型异常数据和离散型异常数据占整体数据量的比例和占异常数据量的比例统计如表1 所示。统计结果进一步证明了上述结论的正确性。
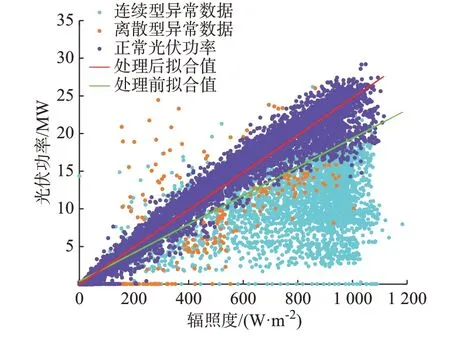
图7 异常数据剔除前后的散点分布和线性拟合Fig.7 Scatter plot distribution and linear fitting before and after removal of abnormal data

图8 典型连续型和离散型异常数据识别时序图Fig.8 Time sequence diagram of identification for typical continuous and discrete abnormal data
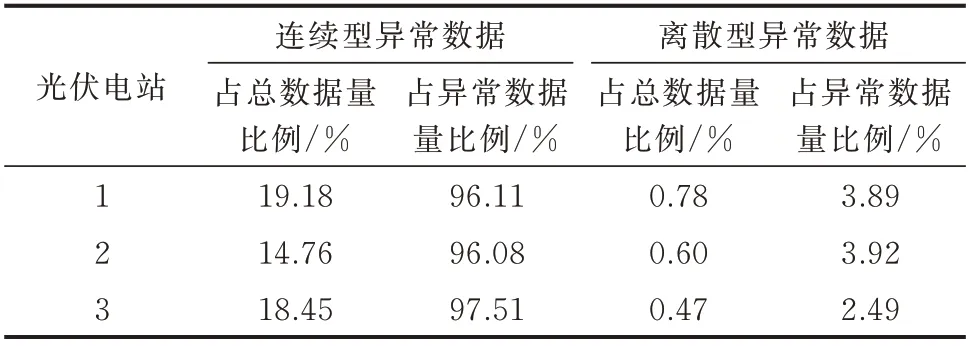
表1 不同类型异常数据占比Table 1 Proportion of different types of abnormal data
3.2 异常数据识别方法对比
采用四分位法、3-Sigma 识别方法与本文所提方法进行对比,3 种方法的识别效果对比如表2 所示。结果表明,本文所提方法对含高比例异常数据的光伏功率识别效果要明显优于四分位法和3-Sigma 方法,且原始数据含异常数据比例越大,本文所提方法的识别效果越好。证明了本文所提方法在异常数据和正常数据界限不明显的光伏电站高比例异常数据识别中的有效性。3 个光伏电站在采用不同异常数据识别方法时,异常数据剔除前后的整体辐照度-光伏功率散点图对比分别见附录D、E和F。

表2 不同异常数据识别方法效果对比Table 2 Effect comparison of different abnormal data identification methods
3.3 异常数据重构效果分析
本文所提方法虽然对与正常数据界限不明显的光伏功率高比例异常数据具有较好的识别效果,但是数据整体的剔除率较高,且容易因相似日划分精度不高导致将正常数据误识别为异常数据,较大程度地破坏了数据的完整性和连续性。为了减小这一影响,可利用异常数据识别后得到的辐照度-光伏功率的线性拟合值对异常数据进行重构。重构方法是采用异常数据剔除后光伏功率的线性拟合值代替识别得到的异常数据,并将小于0 的线性拟合数据置0。
对比数据重构前后,3 个光伏电站辐照度和光伏功率的线性相关程度变化如表3 所示。

表3 异常数据重构前后的线性相关程度对比Table 3 Comparison of linear correlation degree before and after abnormal data reconfiguration
基于图8 中的典型数据,对比异常数据剔除前后光伏功率拟合数据和原始数据如图9 所示。
由图9 可知,异常数据剔除后得到的拟合光伏功率与识别得到的正常光伏功率数据更为接近。由表3 中的结果可得,重构后的辐照度和光伏功率线性相关程度得到了进一步的改善。两种数据重构效果的评价结果均证明了将异常数据剔除后得到的拟合光伏功率数据作为异常数据重构值的可行性。
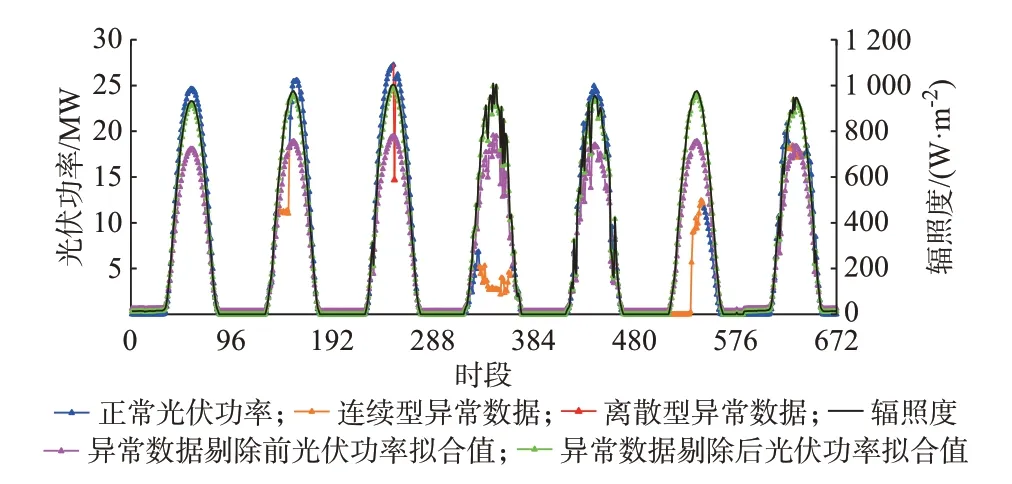
图9 异常数据剔除前后的辐照度-光伏功率拟合效果Fig.9 Radiation-photovoltaic power fitting effect before and after removal of abnormal data
4 结语
为解决以往光伏功率异常数据识别方法难以实现光伏功率高比例异常数据识别的问题,本文提出了基于同时段均值对比算法和四分位法的组合光伏功率异常数据识别方法。在此基础上,利用辐照度和光伏功率的线性相关程度对剔除数据进行了重构。通过实际算例分析得到如下结论:
1)基于光伏功率异常数据的产生原因和时序特性,本文将光伏功率异常数据分为两类,并分别定义为连续型异常数据和离散型异常数据。算例分析结果证明了光伏功率异常数据中,连续型异常数据占比明显高于离散型异常数据。
2)算例分析表明,以辐照度和光伏功率的线性相关程度为判别标准,本文所提异常数据识别方法对具有不同异常数据占比的光伏功率异常数据识别效果均优于四分位法和3-Sigma 法。其中,在高比例异常数据条件下,本文所提方法识别效果更为显著。
3)高比例异常数据条件下,较高的异常数据剔除率在很大程度上破坏了数据的完整性和连续性,采用异常数据剔除后的辐照度-光伏功率线性拟合值进行异常数据的重构,不仅保证了光伏功率数据的完整性和连续性,而且进一步提高了辐照度和光伏功率的线性相关程度,即提高了光伏功率数据质量。
本文在异常数据识别过程中,模型参数的选取仅参照了异常数据剔除率及辐照度和光伏功率的线性相关程度。后续将进一步探讨不同模型参数选取对光伏功率预测精度的影响。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
