基于SolidWorks六自由度机械臂的逆解求解与仿真
2022-10-30赵恩进仲梁维
赵恩进,仲梁维
(200093 上海市 上海理工大学 机械工程学院)
0 引言
近年来,工业机械手在航空航天、机械制造、核环境检测等领域的应用越来越广,因而其工作的高效性、稳定性和精确性也越来越为人所关注。大量科研人员投入精力研究机械手的优化设计及运动学分析,以期获得更稳定、更精确且效率更高的工业机器手[1]。
传统的仿真软件存在缺点。ADAMS 软件通过对末端执行器添加点驱动,设置期望轨迹参数方程,仿真测量得到各个关节角度变化的曲线,通过对曲线的拟合,最终得到运动学逆解[2],结果准确度不高。MATLAB 软件中使用 Robotics Toolbox,进行仿真实验[3],不能真实还原模型。
三维建模软件能够对整个机械手臂及其运动空间进行完整的建模,而且SolidWorks 具备了完善的可二次开发的功能,可以实现机械臂的逆解求解算法与求解后的仿真验证。
本文逆解求解算法采用基于后3 轴相交于一点的6 自由度机械手臂的Pieper's solution[4]解析法,适用于所有具有该种特性的工业机械臂。解析法拥有很高的求解精度[5],因此最适合本文机械臂的逆解求解。在实现逆解求解算法和仿真验证过程中,对于参数的获取和结果的计算主要是通过二次开发技术来实现。通过对SolidWorks 软件提供的API 接口的调用来提取模型特征[6],根据特征参数直接得到或间接求得逆解计算所需参数,将逆解求解结果通过接口对特征赋值来完成仿真验证。
1 机械臂运动学模型建立
本文采用那智不二越MZ07-1-3 型机械臂,该机械臂具有6 个自由度,后3 旋转轴相交于一点,满足3 个关节轴相交且平行的充分条件,可以应用Pieper 准则进行简化[7]。
1.1 机械臂关节坐标系建立和D-H 参数的求解
图1 为在三维模型中建立的D-H 坐标系,使用D-H 模型对机械臂连杆和关节进行建模是一种非常简单的方法,可用于任何构型的机械臂,而与机械臂的结构顺序和复杂程度无关[8]。

图1 模型中建立的坐标系Fig.1 Coordinate system established in the model
图2 为空间中建立的坐标系。每个关节的D-H 坐标系的x,y,z 轴的方向的确定方式为:zi轴为旋转轴的方向,xi轴为与zi,zi+1两轴垂直的方向,其中yi的方向根据右手法则可以进行确定[9]。对于基座坐标系0 让其和第一个关节的坐标系1 原点重合,且z0向和z1方向一致,该坐标系为固定的基座坐标系。
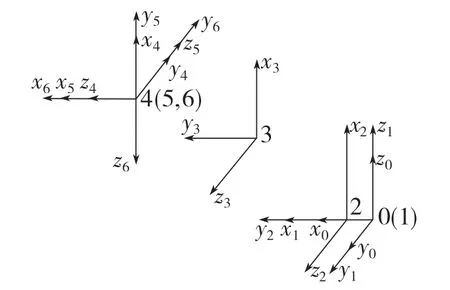
图2 空间D-H 坐标系Fig.2 Spatial D-H coordinate system
根据相邻两坐标系的关系,对坐标系特征进行提取计算求出每两个坐标系之间的D-H参数,表1 为D-H 参数表。其中αi-1表示两相邻坐标系中 zi和zi-1之间的夹角;αi-1表示两相邻坐标系中zi和zi-1之间的空间距离;di为两相邻坐标系中xi和xi-1之间的距离;θi为两相邻坐标系中xi和xi-1之间的空间夹角[10],即为所求逆解。
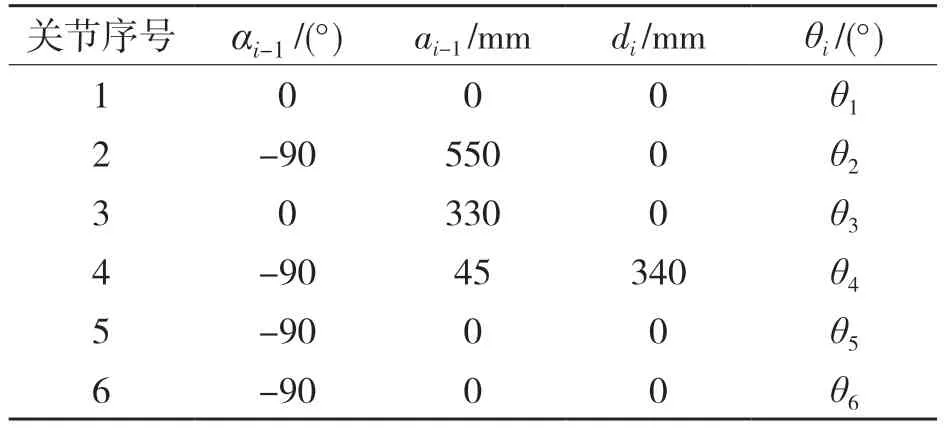
表1 D-H 参数表Tab.1 D-H table
1.2 运动学方程的建立
两坐标系之间的变换矩阵表达式为

SolidWorks API 内置定义的变换矩阵与上述矩阵之间存在转置关系。
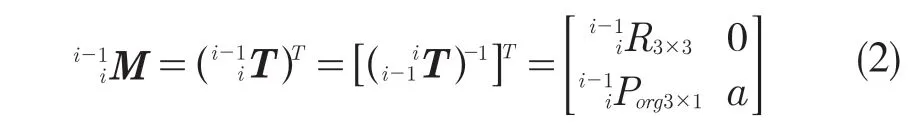
对于后三旋转轴相交于一点的六自由度机械手,满足Pieper 准则,存在封闭解[11]。故采用机械手求逆解的封闭解法。先经过齐次变换求出机械手臂末端坐标系6 和基座坐标系0 之间的齐次变换矩阵,根据位置矩阵求得前3 个角度,然后再根据旋转矩阵对姿态进行求解,求出后3 个解的值。
现根据已知的待求解位置和姿态建立坐标系7,基座坐标系0,坐标系6 相对于坐标系7 的变化矩阵表示机械手末端最后抓取物体时的姿态,是可以设定的常量矩阵。

对于三维模型中坐标系之间的变换矩阵的获取,首先用ModelDocExtension 对象的Ge tCoordinateSystemTransformByName 方法获取一个坐标系相对于世界坐标系的变换矩阵对象MathTransform,该对象是部件变化的接口对象[12]。然后使用MathTransform 对象的Inverse 方法和Multiply 方法完成对矩阵的求逆和乘法运算,以完成对公式的计算。
2 逆向运动学求解算法
2.1 位置角度的求解
机械臂到达的位置由机械手的前3 个角度确定,因此位置角度的求解主要是针对于前3 个角度的求解:

式中:x,y,z ——坐标系的位置坐标。
该机械手臂后三轴相交于一点,建立的坐标系4,5,6 原点相同,所以有
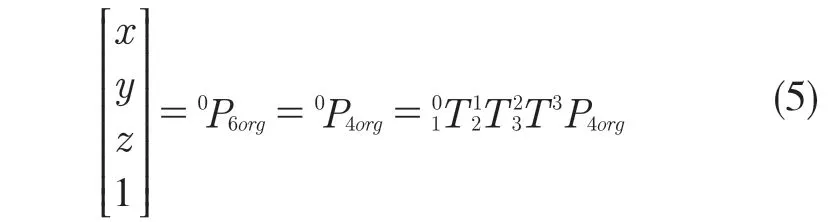
式中,3P4org——坐标系4 的原点坐标在坐标系3中的表达,即为中的第4 列。根据式(1)可得

按照上面的计算方法,依次再将01T12T 用式(1)代入计算得到

令r=x2+y2+z2=(k1c2+k2s2)2a1+k3,联立式(14)—式(16)推出

式(16)为关于角度3 的一元方程,求出角度3,根据r=x2+y2+z2=(k1c2+k2s2)2a1+k3,求出角度2,再根据x=c1u1(θ2,θ3)-s1u2(θ2,θ3)求出角度1。
2.3 姿态角度求解
姿态的求解即为后3 个角度的求解过程,后3 个关节的角度决定了最后的姿态,因此求姿态即为求解后3 个关节的角度。模型中的后3 个坐标系相交于一点,并且是建立在同一个原点的,所以求解后3 个角度即为求解旋转矩阵46R。根据转换关系得

求出旋转矩阵之后根据Z-Y-Z 欧拉角解法即可求出相应的解。
3 SolidWorks 逆解仿真验证
在求出所有的解之后即可用SolidWorks 二次开发技术进行仿真验证。
首先对旋转角度进行定义,定义的方式按照D-H 表达式中对θ角度的定义来进行定义,图3即为其中角度中的一个。

图3 模型中旋转角度的定义Fig.3 Definition of rotation angle in the model
对全部的6 个角度定义之后,利用API 中代表当前模型对象的ModelDoc 接口下的Parameter方法获取代表此尺寸的特征对象Dimension,再用该对象中的方法SetValue3 完成前面求得的角度的赋值。完成6 个角度的赋值,即完成一个给定目标点的仿真验证。图4、图5 给定了起点和终点位置。最终经过计算、运动,得到最后的姿态位置。从图5 看到最终的结果精准度很高。

图4 起始点位和终止点位Fig.4 Start and end points

图5 到达终止点位的姿态Fig.5 Attitude to the termination point
对于一条规划好了的路径,对路径上的每一个目标点,使用程序依次进行读取、计算,将所有计算的结果存储于数据库之中,然后从数据库中进行读取,完成对机械臂角度的赋值,从而实现对整个路径的仿真验证过程。仿真过程的部分图如图6 所示。
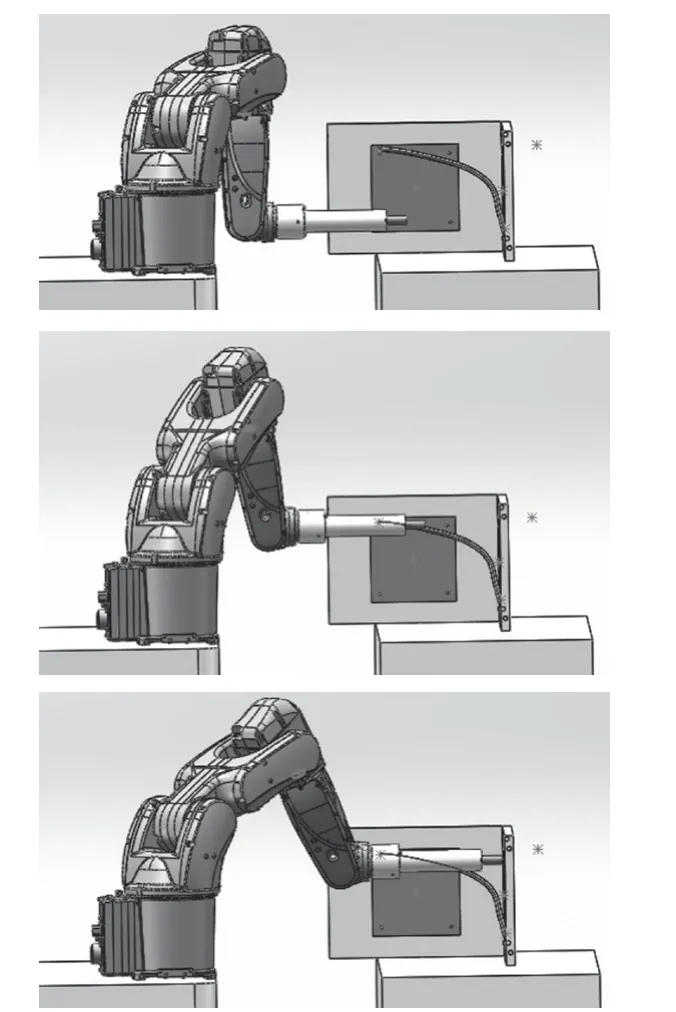
图6 给定路径的仿真过程Fig.6 Simulation process for a given path
图7 为程序的控制界面,首先对机械手的类型进行选择,然后选择是对一个点进行求解还是对整个路径进行求解,对单一路径求解需要输入6 个参数,对全路径进行求解需要选择包含整个路径的文本文件,对路径求解完成后点击移动即可完成最终程序的仿真。

图7 控制程序界面Fig.7 Control program interface
4 结论
利用SolidWorks 的二次开发技术,结合了六自由度机械的逆解求解的算法,实现了对六自由度机械臂的仿真,通过测量验证了仿真结果的可靠性,为六自由度的机械手臂的计算仿真提供了一种新的方法,能够进行真实可靠的模拟仿真实验,为后续路径规划的可靠性提供参考依据。
本文提出的方法还未实现干涉检查功能,路径规划,以及在仿真运动时间上的优化。因此,提高程序运行的效率、实时的运动干涉检查及后续的路径规划是进一步需要研究的方向。
