加筋板封闭矩形声腔的声振耦合特性研究

程传峰，金明，王项如，王园，朱英霞，王健，盘朝奉

（1.246001 安徽省 安庆市 安徽新富新能源科技有限公司；2.246001 安徽省 安庆市 安徽环新集团股份有限公司；3.212013 江苏省 镇江市 江苏大学 机械工程学院；4.212013 江苏省 镇江市 江苏大学 汽车工程研究院）

0 引言

加筋板封闭声腔结构在工程领域中有着大量的应用，如车辆乘座室及其电动汽车液冷板箱、船舶舱室、飞机乘座舱等。在这些加筋板结构与封闭声场构成的声振耦合系统中，板结构不仅要与封闭声场进行耦合，还要与筋进行耦合，导致对耦合系统理论模型进行构建和求解变得比较困难。因此，大量的学者对此类声振耦合系统进行简化研究，包括平板结构与封闭矩形声场构成的经典耦合模型。对于此简化的声振耦合模型，国内外有大量的研究报道，包括板的模态密度和阻尼变化对矩形声场的影响[1-2]，板结构与矩形声场间的耦合特性[1-3]，板的弹性边界约束对耦合系统自由振动和动态响应的影响[4-5]，以及声腔声场的主动控制研究[6-8]等。而对于加筋板结构与封闭声场间耦合的理论研究报道较少，仅有于士甲[9]等提出先利用ANSYS 获得加筋板结构的模态信息，然后再结合能量模态分析法计算加筋板结构与矩形声场所构成耦合系统的动态响应；以及Ma[10]等利用模态叠加法和声振耦合理论建立了双层加筋板与板间矩形隔腔间声振耦合模型，研究了此结构隔声的主动控制。且上述两文献均用耦合系数来表示加筋板结构与声腔声场间耦合强度，但耦合系数只能反映声振耦合在接触面处的模态匹配程度，不能反映真实的耦合强度[1-2]。

加强筋与平板间的耦合会改变板的模态特性，从而对与板结构耦合的封闭声场产生影响。对于筋与平板间耦合，高双[11]等采用里茨能量泛函变分原理对加筋薄板的模态进行求解，并与其它理论结果进行对比分析；Dozio[12]等基于模态叠加法研究了有限尺寸加筋薄板的自由振动特性；Lin 分别基于模态叠加法[13]、传播波法[14]研究了激励形式和激励到筋的距离对加筋板结构动态响应的影响，研究表明激励到筋的距离和板的振动响应密切相关。此外，还有微分求积法[15]、改进的傅里叶级数法[16-17]等用于筋与板间耦合分析。由上述文献研究可知，加筋对板结构与矩形声场间耦合强度的影响，以及激励到筋的距离对与板结构耦合的封闭声场响应的影响，国内外鲜有这些方面的报道。

本文对加筋板结构与封闭矩形声场间的声振耦合特性进行详细研究，首先利用模态叠加法建立加筋板结构的理论模型；然后利用声振耦合理论建立加筋板结构与声腔声场间耦合模型，并通过软件仿真验证所构建理论模型的准确性。基于构建的声振耦合模型研究了激励到加强筋的距离对耦合系统中板振动能量和声腔声场能量的影响。此外，推导了反映加筋板结构与矩形声场间耦合强度的传递因子计算公式，研究了板实施加筋对耦合强度的影响。

1 模型建立

设矩形声腔z=Lz处为加筋弹性壁面，其余为刚性壁面，板的边界实施简支约束。加强筋位于板的一侧，并设筋与板之间为不可滑动的线连接，在连接处xb存在相互作用的线力Fc和线力矩Me，如图1 所示。矩形声腔内声场波动方程和基板的振动微分方程分别为[10]

图1 结构-声耦合系统模型Fig.1 Structure-acoustic coupled model

式中：p，c0——矩形声腔内声场声压和声场声速；D，ρ，h，w——板的弯曲刚度、密度、厚度和振动位移；fp——作用在板上（x0，y0）处的点力。

对于加强筋，其弯曲、扭转振动微分方程分别为[12]

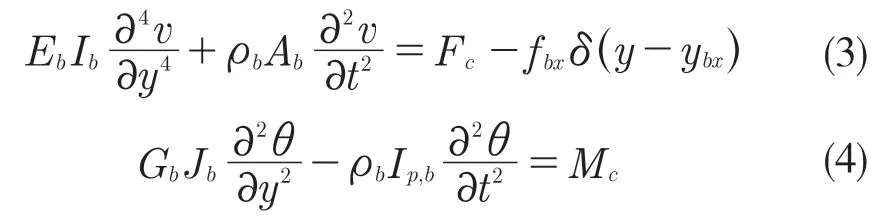
式中：v，θ——加强筋的弯曲位移和扭转角度；Eb，Ib，ρb，Ab——筋的杨氏模量、截面惯性矩、密度和横截面积；Gb，Jb，Ip,b——筋的剪切模量、圣维南扭曲常数、极惯性矩；fbx——作用在加强筋的ybx处点力。

矩形声场p 可通过模态叠加法扩展得到[2]

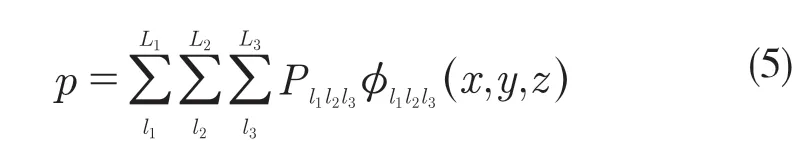
解法六：由函数图象的对称性可知函数图象上与对称轴距离相等两点的函数值相等，即：，则在中，任取可求出a=-1.

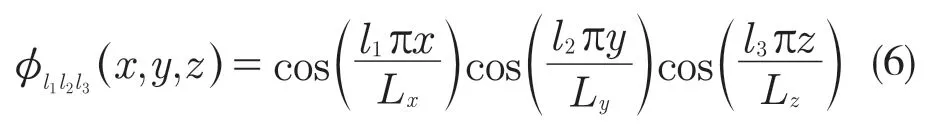
基于模态叠加理论，基板振动位移w（x，y，t）和加强筋振动位移v（y，t）、扭转角度θ（y，t）可分别扩展为[12]

式中：φij（x，y）=φi（x）φj（y），φi（x）=sin（iπx/Lx），φj（y）=sin（jπy/Ly）；Wij，Vj，θb,j——对应的基板振动位移模态幅值、筋振动位移和扭转角的模态幅值。

对于矩形声腔内声场，考虑其边界条件，利用声模态函数的正交性和第二格林定理，并引入模态损耗因子可得

将梁的弯曲和扭转运动方程式（3）和式（4）代入式（2），再代入基板和梁的模态振型函数式（7）、式（8）和式（9），然后方程两侧乘以板的模态振型函数，并对板面进行积分，利用模态振型的正交性，以及基板和加强筋在接触处转角和位移连续性条件[12]

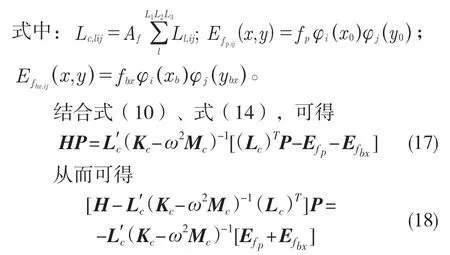
通过式（18）可得到矩形声腔内声场声压模态幅值，将此声场模态幅值代入式（14）即可得到加筋板的振动位移模态幅值。然后将求得的矩形声场和加筋板振动位移的模态幅值分别代入式（5）和式（7）即可得到声场声压和板振动位移。

2 理论计算与分析

如图1 所示，设简支约束加筋板的尺寸为：Lx=0.78 m，Ly=0.91 m，声腔高度Lz=0.55 m。基板厚度h=0.003 m。筋是截面为Ab=0.003×0.036 m2的矩形。基板和筋材料均为铝，密度ρ=2 770 kg/m3，杨氏模量为E=71 GPa，泊松比为μ=0.33。设声腔声场和板的模态损耗因子分别为0.001 和0.01。在板（0.1，0.8）m 处作用一幅值为1 N 的法向简谐点力fp，且分析过程中点力保持不变。

本文用于矩形声场、基板、筋间耦合计算的模态个数上限分别取为L1×L2×L3=5×5×5，I=J=10，J=10。为验证准确性，用商业软件对声振耦合系统进行建模仿真，设筋位于基板xb=Lx/4 m 处。图2 为两种方法计算的点力激励下声腔内场点1（0.1，0.1，0.1）m，2（0.39，0.455，0.275）m 处的声压级，可知结果吻合较好，说明此理论模型是准确的。

图2 解析法和数值法结果对比Fig.2 Comparison of analytical and numerical results

2.1 加筋板结构与矩形声场间模态耦合特性

2.1.1 耦合系数

模态耦合系数是声腔声场模态和加筋板结构模态在接触面上的匹配程度[1-2]。板实施加筋后，其模态振型变得比较复杂，使得加筋前后板的耦合选择性发生变化。因此这里推导了加筋板结构与矩形声场间模态耦合系数公式，定义第l1l2l3阶矩形声场模态和第ij 阶加筋板模态间的耦合系数为

表1 为加筋板结构（xb=Lx/4 m）与矩形声场间的耦合系数，可知加筋板结构与矩形声场间的耦合系数在Y 轴向仍然满足只有模态序数之和为奇数时，其耦合系数才不为零。而在由于加筋改变模态振型的X 轴向，其模态序数之和为偶数时，加筋板模态和矩形声场模态间也有可能存在耦合，如声腔模态（0，0，0）和板模态（2，1）、声腔模态（1，0，0）和板模态（1，1）等在加筋后其耦合系数变为非零。

2.1.2 传递因子

平板结构与矩形声场间可用传递因子反映模态间的耦合强度[1-2]。由于平板结构与矩形声场间传递因子公式不再适合于加筋板时情况，因此本文推导了加筋板结构与矩形声场间传递因子公式。定义第l1l2l3阶矩形声场模态和第ij 阶加筋板模态间的传递因子为：

表2 为加筋板结构（xb=Lx/4 m）与矩形声场模态间的传递因子，相较于平板与矩形声腔间耦合，可得

（1）加筋后更多的板模态与声场模态间产生了耦合，如声场模态（1，0，0）和板模态（1，1）、（5，1）、（1，3）间传递因子均不为零，对应表1中它们间的耦合系数在板实施加筋后亦不为零；但加筋后新出现耦合间传递因子均较小，如表2所示。

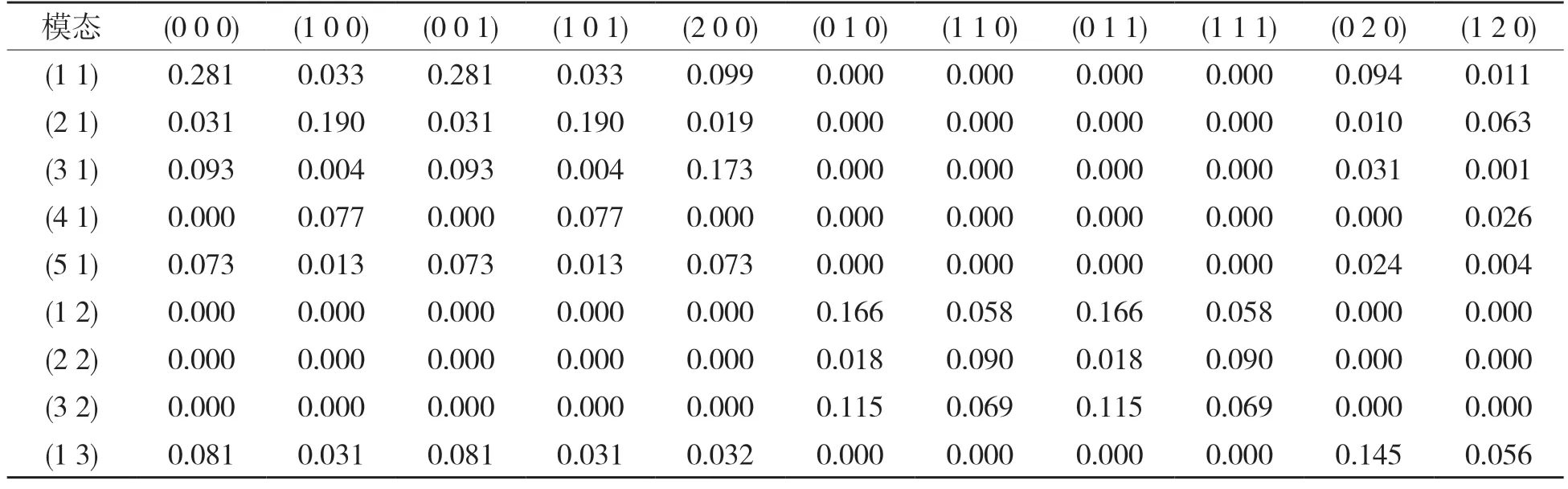
表1 加筋板与矩形声场间模态耦合系数,xb=Lx/4 mTab.1 Coupling coefficients between modes of rectangular cavity and ribbed plate,xb=Lx/4 m

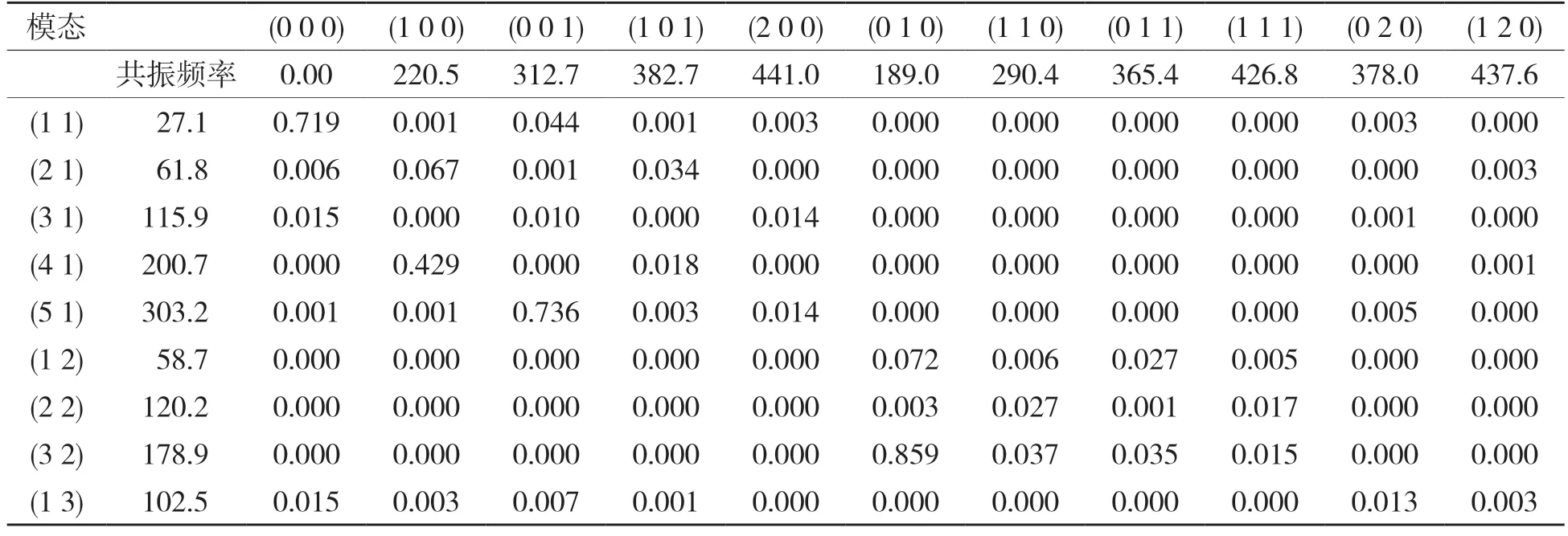
表2 加筋板结构与矩形声场模态间传递因子，xb=Lx/4 mTab.2 Transfer factors between modes of ribbed plate and rectangular cavity,xb=Lx/4 m

（2）传递因子越大，耦合越强，对应耦合前共振频率差越小；例如声腔模态(0,1,0)和板模态(3,2)间传递因子加筋前后分别为0.084 和0.859，对应耦合前共振频率差分别为45.84，10 Hz。

2.2 筋到激励的距离对耦合系统动态响应的影响

设加筋后的板振动能量衰减级LTp[13]和矩形声腔声场声势能衰减级LEe分别为

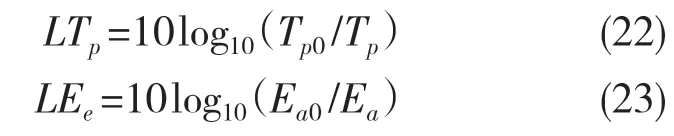
式中：Tp，Ea——加筋板与矩形声腔构成耦合系统中板振动能量和声腔声势能[2]；Tp0，Ea0——平板与矩形声腔构成耦合系统中各部分对应能量。

图3、图4 分别为耦合系统中基板振动和矩形声场的能量衰减后及衰减前的曲线，横坐标分别采用1/3 倍频程和连续频谱的形式。令筋在基板上布放位置分别为xb=0.1，xb=Lx/4，xb=3Lx/4 m，对应点力激励加强筋上、点力距筋较近和较远三种情况。由于加强筋位于 xb=Lx/4 m 和xb=3Lx/4 m时关于板是对称的，可知两加筋板的共振频率一样，模态振型对称。由图3 和图4 分析可得：

（1）当点力作用在加强筋上时（xb=0.1 m），相较于平板，除了中心频率63 Hz 处以外，矩形声场和基板振动的能量级在整个分析频段出现了衰减现象（正LEe和LTp值），如图3（a）和（b）所示。此时加筋板的动态响应是由筋弯曲刚度所控制[13-14]，且筋的弯曲刚度是基板的4.6 倍，从而板振动和与其耦合的声腔声场的能量均在加筋后变小。由图4（a）知，板控模态（2，1）的共振频率从加筋前的56 Hz 变为加筋后的58 Hz，分别位于中心频率50 Hz 和63 Hz 内，使得加筋后中心频率63 Hz 处出现能量放大的现象。

图3 声场声势能衰减级和振动能量衰减级Fig.3 Attenuation level of acoustic potential energy and plate vibration energy

（2）加强筋位于xb=Lx/4 m 时，相较于平板，除中心频率63，160 Hz 外，声腔声场和板振动的能量在200 Hz 以下其他中心频率处出现了明显的衰减现象；中心频率200 Hz 范围内的202 Hz对应板的1/4 弯曲波长λp/4=0.095 m，为点力到筋的距离；由文献[13,14]可知，此时加筋板的振动响应是由筋的弯曲刚度所控制的，且筋的弯曲刚度远大于板的，因此导致加筋后的板振动能量以及与其耦合的声腔声能量在此中心频率下出现衰减现象；类似于筋位于xb=0.1 m 处，中心频率63 Hz 处出现能量放大现象是由于加筋使板控模态（2，1）的共振频率出现转移导致的，如图4（b）所示；但中心频率160 Hz 处出现的能量放大现象是由加筋后板控模态（3，2）产生较大的声势能导致的，板控模态（3，2）加筋前后的共振频率142，175 Hz均在中心频率160 Hz范围内。

图4 加筋前以及不同加强筋位置时，矩形声场声势能级Fig.4 Acoustic potential energy level with unribbed and ribbed of different locations

（3）当加强筋位于xb=3Lx/4 m 时，声腔声能量和板振动能量相对于平板时没有在整个频段连续出现能量衰减现象；这是因为此时点力到筋的距离远大于板的1/4 弯曲波长，导致加筋板振动响应是由基板的弯曲刚度所控制；且加筋会使板控模态的共振频率从一个中心频率转移到另外一个中心频率范围内，从而使加筋前后能量出现波动现象，如图4（c）所示。相较于筋位于xb=Lx/4 m 时，虽然两个加筋位置处板的自由振动特性一样，但它们到激励的距离不同，导致对应耦合系统的响应也不同。

3 结论

本文基于模态叠加法和声振耦合理论构建了加筋板结构与矩形声场间耦合模型，研究了加筋对声振耦合特性和受激励后动态响应的影响。结论如下：

（1）由于加筋导致的板结构与矩形声场间耦合特性变化与筋的布放位置有关；在与筋平行的轴向，板结构与矩形声场间模态耦合仍然具有选择性，而在其它轴向耦合不再有选择性；加筋后板结构与矩形声场间耦合强度（传递因子）发生了改变，但由于耦合选择性改变而增加的板结构与声场模态耦合间能量传递较少。

（2）由于加筋而产生的矩形声场声势能和加筋板振动能量的衰减程度与点力到加强筋的距离密切相关，当筋的弯曲刚度远大于板的弯曲刚度，且点力直接作用在加强筋上或者点力到筋的距离小于板的1/4 弯曲波长时，声腔声势能和板振动能量在所分析的大部分频段都得到了衰减；反之则不会出现连续衰减现象。从而可为工程中的加筋板封闭空腔这类声学结构设计时筋的合理布置提供了指导。