基于Workbench的双转子系统临界转速的求解与分析

2022-10-30刘杰

农业装备与车辆工程 2022年6期

刘杰

（200093 上海市上海理工大学机械工程学院）

0 引言

旋转机械，如航空发动机、风机涡轮机、发电机组等在现代工业中占有举足轻重的地位。航空发动机更是当今我国需要大力发展的项目之一，双转子结构又是需要重点研究的对象，其中临界转速作为双转子的一个重要动力学特征，引发了学者的广泛研究。由于发动机的正常工作转速通常要跨过系统的1 阶甚至2 阶转速，因此了解双转子系统的临界转速以及系统参数对它的影响，对于研究双转子结构的动态特征有显著作用。

近几十年来，针对航空发动机双转子系统临界转速的求解，许多学者做了大量研究。杨喜关[1]等人采用ANSYS 软件推导的有限梁模型建立了双转子系统，然后基于固定界面模态综合法的模型降阶，讨论了模态截止频率和瞬态分析的影响；孙传宗[2]等人借助Craig-Bampton 模态综合并通过对比临界转速和振型说明了所组建模型的准确性；YANG[3]等人针对非对称模型，为减小矩阵的大小，采用有限元法和模态转换技术进行建模求解；GUSKOV[4]等人通过有限元仿真模拟和实验研究了双转子系统的自然特性；FERRARIS[5]等人利用坎贝尔图和质量不平衡响应，分析了非对称双转子系统的动态特性；林荣洲[6]借用有限元方法，研究了机匣参数的变化对双转子结构系统的影响；戚胜[7]等人分析了转子在正转和反转的情况下，系统动力学特征的变化；石怀涛[8]等人为了降低传统求解临界转速方法带来的误差，采用Riccati 传递矩阵法将求解精度大幅度提高；王存[9]针对临界转速的求解问题，提出了直接法和完全法，并通过谐响应分析进行了验证。

本文针对双转子系统动力学响应求解问题，采用ANSYS Workbench 进行有限元仿真求解，得到双转子系统的主振型图和Campbell 图，同时通过改变支撑刚度探究了支承刚度对临界转速的影响。

1 双转子系统模型

1.1 三维模型

采用SolidWorks 三维软件建立了如图1 所示的航空发动机双转子模型。该双转子系统由低压转轴、高压转轴以及2 个支撑轴承和1 个中介轴承组成。低压转轴上有2 个圆盘，高压转轴上有8 个圆盘，其中低压转子和高压转子通过中介轴承3 连接，低压转子通过轴承1 和轴承2 进行支撑。

图1 双转子系统三维模型Fig.1 Three-dimensional model of dual rotor system

1.2 有限元模型

1.2.1 动力学模型

由于航空发动机双转子系统的内部结构太过复杂，因此很多研究学者采用简化版的双转子系统有限元模型进行建模分析，建模后得到系统的动力学方程如下：

式中：M——质量矩阵；C——阻尼矩阵；K——刚度矩阵。

1.2.2 有限元简化模型

在计算系统临界转速前，为了计算的方便与快捷，首先需要将系统的三维模型进行简化。在该模型中，转轴采用Beam188 单元代替，圆盘采用集中质量单元Mass21 进行代替，支撑轴承和低压和高压的中介轴承采用combin14 单元进行代替。其中，转子的整体简化模型如图2，combin14 单元模型的结构示意图如图3 所示。

图2 双转子系统有限元模型Fig.2 Finite element model of dual rotor system

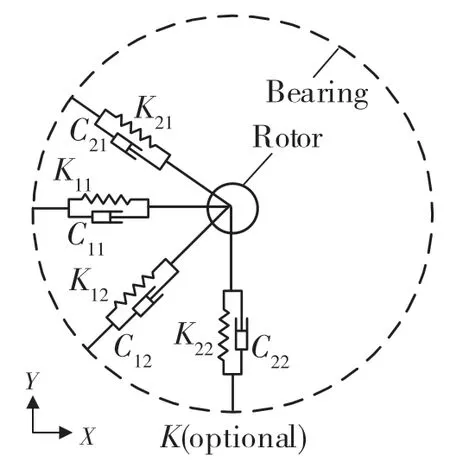
图3 Combin14 单元模型Fig.3 Combin14 cell model

2 仿真结果

求解临界转速之前，第1 步要确定系统中零件的材料属性。双转子系统中转轴的材料为2Cr13，其材料属性如表1 所示；第2 步进行网格划分；第3 步在低压转子两端设置支撑刚度，Kyy=Kzz=1×107N/m；第4 步在低压转子两端设置约束。

表1 材料2Cr13 的属性Tab.1 Properties of material 2Cr13

2.1 模态分析

当转子系统没有阻尼时，此时系统的固有频率求解。系统的运动微分方程为

式中：M——系统的质量矩阵；C——系统的阻尼矩阵；K——系统的刚度矩阵；X——位移响应量；F——激振力。

当式（2）中的阻尼C=0 时，方程如下：

故可得方程的解为

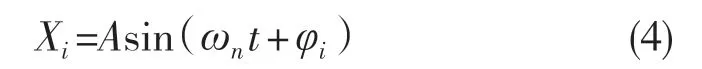
将式（4）代入式（3），可得式（5）：

因为一个振动系统的振幅不全为零，必有

通过ANSYS Workbench 软件采用QR 阻尼法分别计算了双转子前6 阶模态。其中低压转子振型图如图4，高压转子振型图如图5 所示。

图4 低压转子振型图Fig.4 Vibration mode diagram of low-pressure rotor

图5 高压转子振型图Fig.5 Vibration mode diagram of high-pressure rotor

从图4 可见，随着模态阶数的增大，转子系统的变形程度愈加严重。在1 阶模态内，转子沿Y-Z平面振动弯曲，变形最严重的位置在圆盘上。在2 阶模态内，转子沿着X-Z平面振动弯曲，变形最严重的位置在靠近圆盘处。在3 阶模态内，转子沿着Y-Z平面振动弯曲，变形最严重的部位在转轴上。在4 阶模态内，转子出现了沿着X-Z平面向内凹陷的变形。在5 阶模态内，转子出现了沿着X-Z平面凹陷的变形，在6 阶模态内，转子沿着X-Z振动弯曲，且转轴上呈现严重的变形现象。

从图5 可知，随着主振型的阶数增大，转子的变形程度愈加严重。在1 阶模态内，转子出现了沿着Y-Z平面向内凹陷的现象；在2 阶模态内，转子出现了沿着Y-Z平面向内凹陷的现象；在3阶模态内，转子沿着X-Z平面向内凹陷的现象；在4 阶模态内，转子沿着X-Z平面向内凹陷；在5 阶模态内，转子沿着X-Z平面向内凹陷，且转轴出现明显变形；在6 阶模态内，转子沿着X-Z平面向内凹陷。

2.2 临界转速

通过有限元方法求解得到的Campbell 图中，转子系统会出现正进动（FW）和反进动（BW），最后绘制得到的低压与高压转子的Campbell 图如图6、图7 所示。

图6 低压转子Campbell 图Fig.6 C ampbell diagram of low-pressure rotor

图7 高压转子Campbell 图Fig.7 Campbell diagram of high-pressure rotor

通过图6 和图7 可以得到系统的临界转速如表2 所示。

表2 转子的临界转速Tab.2 Critical speed of rotor

3 系统参数对临界转速影响的分析

转子的工作转速在临界转速范围内会发生振动现象，严重时会使转子系统发生破环，造成机毁人亡的事故，因此关于系统固有因素对临界转速影响的研究就显得格外重要。本文中双转子系统的低压转轴采用轴承支撑，这导致低压转子的临界转速一定与支撑轴承特性之一的支撑刚度有关。研究临界转速随支撑刚度的变化趋势，就可以通过改变支撑刚度来调整转子系统临界转速，使转子系统远离临界转速，达到系统平稳运行的安全要求。

由图8 可知，随着刚度由1×107N/m 增加到1×108N/m，系统的临界转速也在逐渐增大。刚度为1×107N/m 时，系统的2 阶转速为97.35 rad/s，而3 阶转速突然增长到180.3 rad/s；刚度为3×107N/m时，系统的2 阶转速为143.76 rad/s，此时3 阶转速为199.3 rad/s；刚度为5×107N/m 时，系统的2 阶转速为159.51 rad/s，此时3 阶转速为210.91 rad/s；刚度为1×108N/m 时，系统的2 阶转速为169.8 rad/s，此时3 阶转速为222.24 rad/s。对比不同刚度下的转速可以看出，刚度逐渐增大，转速增值不断减小。