股骨假体仿生微结构设计与分析

李佳意，董万鹏，陈秋平，任梦，张吉超

（201620 上海市 上海工程技术大学 材料工程学院）

0 引言

髋关节炎属于骨关节炎性疾病，是如今十分常见的一种慢性关节疾病。人工髋关节置换术（Total Hip Arthroplasty,THA）是目前最主要的手术治疗方法，可以直接有效地恢复病人的关节功能，还可以避免一系列的临床并发症[1]。人工髋关节置换术虽然成为了一种成熟的治疗手段，但是仍然存在着一些问题，最常见的是假体不匹配和假体松动，引起假体松动和不匹配的主要是假体的标准化设计以及假体缺少自然骨中的松质骨结构[2]。常用的金属假体Ti-6Al-4V 弹性模量为109 GPa，比股骨硬6～7倍，高硬度的假体容易产生骨生长不良、应力屏蔽、骨折等风险[3]。众多研究通过使用复合材料、多孔生物材料及功能梯度材料降低股骨假体的硬度[4-5]，但很少有研究通过多孔结构的设计降低刚度[6]，本文通过采用仿生设计理念对髋关节模型进行定制化设计，借鉴晶体结构设计理念，通过设计不同的孔隙结构来降低假体的弹性模量，从而降低硬度。并通过有限元分析方法验证结构的弹性模量、屈服强度和强度极限。

1 模型建立

1.1 仿生微结构模型

建立的仿生微结构分别为六面体立方仿生微结构、面心立方仿生微结构以及体心立方仿生微结构。仿生微结构的单元结构通过SolidWorks 建立模型，每个单元的边长以1.45 mm 为基础，建立的单元结构模型如图1 所示。

图1 单元结构模型Fig.1 Unit structure model

1.2 仿生微结构参数设计

1.2.1 模型总体尺寸

MEHBOOB[7]等对不同数量的BCC 立方体单元模型进行了有效力学性能的灵敏度分析，每个立方体组合后尺寸分别为4×4×4，8×8×8，12×12×12，16×16×16（mm）的BCC 结构。研究发现，不同尺寸BCC 结构没有改变单元模型有效的机械性能。因此，本研究分别对单元模型进行整列及整合，得到目标模型，如图2 所示。以7 为单位进行阵列，建立10.15×10.15×10.15（mm）模型。利用SolidWorks 把模型合并为一个实体，并导出为xt 文件格式。

图2 合并模型图Fig.2 Merged model diagram

1.2.2 孔隙率

研究表明，仿生多孔结构内部空洞相互连通，有利于骨的生长，也有利于具有刺激细胞生长的生长因子和营养物质进入结构的内部，促进骨细胞的生长繁殖[8]。BRAGDON[9]等研究认为，满足骨骼生长的仿生多孔结构的孔隙率应当大于40%；美国医疗药物管理局（FDA）认为，多孔股骨假体的孔隙率范围在30%～70%有利于骨细胞的生长[10]。SIMONEAU[11]等认为仿生多孔结构的孔隙率在30%～50%更有利于骨重建，可提高结构的比表面积。

本研究从模型的质量公式入手，通过选用相同的材料，质量比与体积比一致。质量与体积的关系为

式中：M——模型质量；ρ——材料密度；V——模型体积。

由于材料一致，各模型的材料密度相同。模型孔隙度的公式为

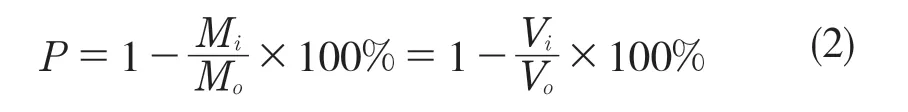
式中：P——孔隙率；M0——实体模型的质量；Mi——仿生微结构的质量（1≤i≤3）；V0——实体模型的体积（为1 045.7 mm3）；Vi——仿生微结构的体积。

通过计算得到的3 种模型的体积和孔隙率如表1 所示，通过控制单位模型的支柱尺寸保证3 种仿生微结构，六面体立方、面心立方、体心立方的孔隙率一致。

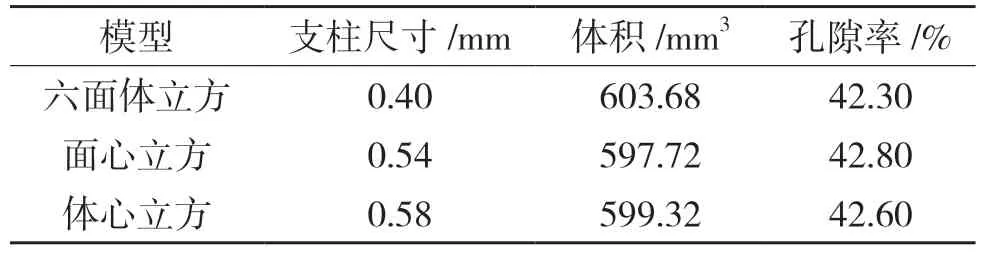
表1 模型基础参数Tab.1 Basic parameters of model

2 ANSYS 有限元模拟

2.1 材料

常用髋关节股骨假体材料很多，主要包括超高分子量聚乙烯、医用金属材料和医用陶瓷材料[12]。Ti-6Al-4V 具有良好的耐磨性能，使其在生物医疗领域中起着至关重要的作用，常用作于髋关节植入物[13]，其密度为4 440 kg/m3，弹性模量为109 GPa，泊松比为0.34[14]。Ti-6Al-4V 材料的塑性采用多线性各向同性分布，如图3 所示。

图3 Ti-6Al-4V 塑性属性Fig.3 Plastic properties of Ti-6Al-4V

2.2 边界条件与载荷

为了探究微仿生结构的力学性能，本研究通过ANSYS 模拟结构在万能试验机上的压缩实验。在仿生微结构的上表面施加4.5 mm 的垂直位移载荷，下表面采用完全约束[15]，模拟计算仿生微结构的弹性模量[16]、强度极限[17]和屈服强度[18]。

2.3 有限元分析结果

在ANSYS 中分别对六面体立方、面心立方和体心立方的基础分析参数设置，划分网格大小为0.3 mm。发现在3 种模型孔隙率类似的情况下，六面体立方的网格数量最少，比面心立方减少了23.8%，比体心立方减少了8.3%。模型的计算时间从低到高分别为六面体立方、体心立方和面心立方。面心立方节点数量和网格数量大是由于面心立方单元结构复杂，模型在转连接处的网格生成困难，节点增加。

六面体立方、面心立方和体心立方的米塞斯应力以及变形如图4 所示。六面体立方(图4（a）和图4（b））最大位移量为4.514 3 mm，达到屈服时的最大von Mises 应力为1 127.2 MPa；面心立方(图4（c）和图4（d））最大位移量为4.663 7 mm，达到屈服时的最大von Mises 应力为1 083.7 MPa；体心立方(图4（e）和（f））最大位移量为4.894 6 mm，达到屈服的最大von Mises 应力为1 227.2 MPa。在位移分布上，六面体立方变形在压力方向呈现线性分布，层次分明；面心立方和体心立方变形在压力方向呈现非线性分布，变形局部不均匀；在应力分布上，3 个模型的应力分布总体均匀，六面体立方和面心立方结构的最大应力皆呈现在模型表面，体心立方结构最大应力分布在模型内部（单元模型连接处）。

图4 模型应力与变形云图Fig.8 Model stress and deformation nephogram

3 种模型的应力应变曲线如图5 所示，结构的应力应变通过式（3）和式（4）计算得。

图5 应力应变曲线Fig.5 Stress-strain curve

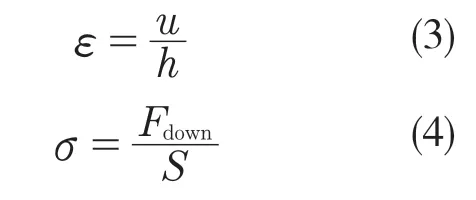
式中：ε——结构的应变；u——模拟完成后结构上表面的位移；h——结构的高度；σ——结构的应力；Fdown——结构下表面总的反作用力；S——结构的底面积。

弹性模量是用来衡量物体抵抗弹性变形的能力，将假体的弹性模量通过结构优化降低到与真实骨骼的模量相近，可有效避免应力遮挡反应。HUISKES[19]通过实验证明股骨假体刚度越低，界面应力越大，越容易使假体产生微动，提出了假体材料的弹性模量在40.0 GPa 时，应力遮挡最小、界面应力最合适。计算得到：六面体立方的弹性模量约为24.6 GPa；面心立方的弹性约为24.2 GPa，比六面体立方减少1.6%；体心立方的弹性模量约为22.2 GPa，比六面体立方减少9.8%。人体真实皮质骨的弹性模量为17.0 GPa[20]，本文研究的3 种仿生微结构模型的弹性模量与人体真实骨骼相近，能有效降低应力遮挡，在相同的孔隙率的条件下，体心立方的弹性模量最小。

屈服强度是指结构出现屈服现象时的屈服极限，屈服强度越大，结构越稳定，越不易发生破坏。本文取塑性应变为0.2%时对应的应力为模型的屈服应力[21]。六面体立方的屈服强度为435.7 MPa；面心立方的屈服强度为428.8 MPa；体心立方的屈服强度为393.3 MPa。六面体立方的屈服强度最大，面心立方次之，体心立方最小。分析显示，六面体立方的稳定性最大，体心立方更容易失稳。

强度极限是指物体在外力作用下发生破坏现象时产生的最大应力，本文所做压缩模拟，强度极限即为抗压强度极限。根据应力-应变曲线可得：抗压强度极限面心立方＞六面体立方＞体心立方，分别为483.3，471.2，468.3 MPa。

3 讨论

本文设计和分析3 种仿生微结构，在外力作用下，对3 种仿生微结构的性能进行了有限元分析，分析结果如表2 所示。

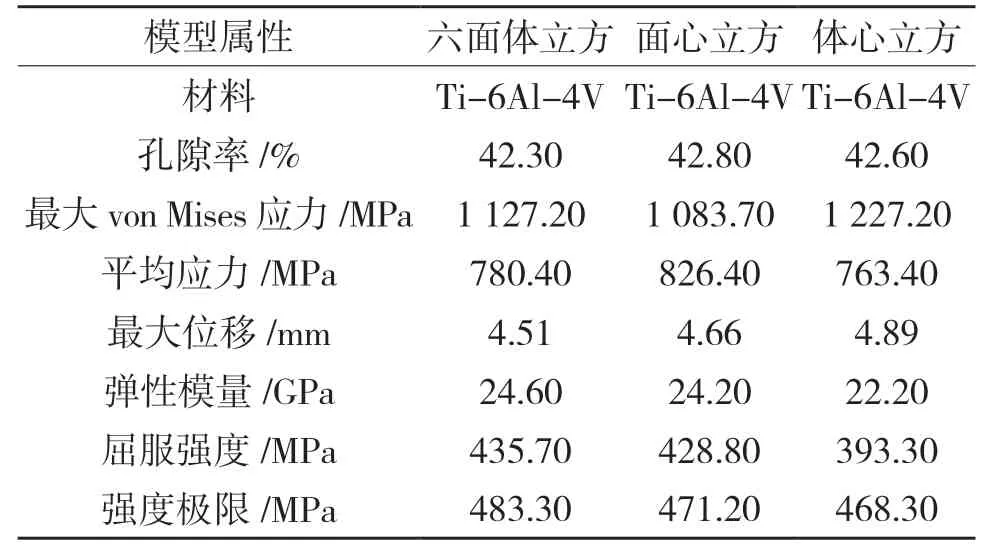
表2 有限元分析结果Tab.2 Results of finite element analysis

由表2 可知，3 种模型的孔隙率保持在42.5%左右。相关研究表明，在术后骨骼重建中，多孔结构的孔隙率在40%～80%有利于促进骨骼的内生长，有利于假体与骨骼的融合[22]。WANG[23]等通过研究股骨柄的骨-植入物界面的相对微动和骨密度损失发现，具有50%和60%孔隙率模型的多孔杆增加了过度微动的风险，导致植入物不稳定。本文所设计的体心立方、面心立方以及六面体模型符合要求，有利于促进骨骼生长。

表2 中六面体立方、面心立方和体心立方的弹性模量分别为24.6，24.2，22.2 GPa，在相同的边界条件下，体心立方能够获得更低的弹性模量，即能够更有效降低假体的弹性模量，减少应力遮挡不良现象。MEHBOOB 等研究孔隙率为18%、30%、47%、63%、77% 和90% 的Ti-6Al-4V 体心立方多孔结构的[24]力学性能，所对应的弹性模量分别为76.7，53.8，31.5，18.3，9.1，3.8 GPa；钟望坤[25]等通过有限元仿真发现，随着孔隙率的增高，梁单元直径变小，受力更易变形，模型的等效弹性模量减少；HUISKES[26]通过实验证明假体的刚度越低，则在股骨界面应力越大，而界面应力越大，越容易使假体产生微动，提出假体材料在 40.0 GPa 时，应力遮挡最小、界面应力最适合这一观点。本文所设计的孔隙率42.6%的体心立方结构的弹性模量符合MEHBOOB，HUISKES 等研究的结论，证实了本实验的可行性。

表2 中3 种模型中最大屈服强度以及最大强度极限都为六面体立方结构，证实六面体立方在3 个模型中的刚度最大，即承载能力最强，等效弹性模量最高。证实了六面体立方在压缩实验中的力学性能优良且稳定性较好，但剪切性能较差[27]。以弹性模量为参考标准而言，在符合假体所要求的屈服强度下，屈服强度与弹性模量越低，应力遮挡越少。本文所设计的3 种模型的屈服强度都符合股骨假体（150～500 MPa）[28]的性能要求，3 种模型都有效降低了弹性模量，其中体心立方结构比起其余两种更适合作为假体模型。

4 结论

本研究提出并设计3 种新型仿生微结构，保持3 个设计模型的孔隙率一致，通过ANSYS 分析模型的变形，von Mises 应力，通过相关公式比较3种模型的弹性模量、屈服强度以及抗压强度极限。实验结果显示，孔隙率为43%的3 种仿生微结构的弹性模量有效降低到了人体皮质骨弹性模量附近，可有效减少应力遮挡现象。通过比较3 种模型的屈服强度、位移等，六面体立方的稳定性和抗压强度高于其他两种结构，体心立方的等效弹性模量最小，在强度合适的条件下，体心立方结构更适合充当股骨假体的设计模型。本研究所设计的仿生微结构模型对股骨植入物的设计有一定的参考价值，能够有效降低模型等效弹性模量，减少应力遮挡。

但本研究只牵涉到理论设计与分析，没有涉及实际制造。选择性激光熔融（SLM）是一种常用于制造复杂模型的增材制造方法，在后续的研究中，通过SLM制造仿生微结构可以作为一个研究方向。