基于惯导技术的水田拖拉机下陷深度检测方法

孙恒辉，宿宁，张耀文，张雷，黄伟

（1.230031 安徽省 合肥市 中国科学院合肥物质科学研究院；2.230031 安徽省 合肥市 中科合肥智慧农业谷有限责任公司）

0 引言

下陷深度是反映拖拉机通过性能的重要指标。拖拉机行驶过程中出现下陷时，其行驶阻力随下陷深度增加而增加[1-3]。水田环境下的土壤水分过大、土壤坚实度小呈烂泥状，拖拉机在此类土壤上行驶时容易发生过度滑转和严重下沉，轻则增加能耗和操作难度，重则导致拖拉机无法行驶。

对下陷深度的实时监测不仅有助于提高水田拖拉机的实时操作性，以降低油耗、提高作业效率，同时也可以为研究水田行走机具与水田泥土之间的作用关系提供必要的实验数据，有助于设计通过性更好、作业效率更高的水田拖拉机[4-8]。

水田环境中一直有水的存在，受到拖拉机运动的干扰，水面会产生大幅度波动，此时传统的光、超声波、视觉等测距方法不能应用到水田环境。此外，拖拉机在烂泥状水田土壤上行驶时容易出现车体向一侧倾斜的现象，这使得适用于旱地等硬质地面的接触式检测方式如五轮仪由于轮面不能贴合地面而产生很大的检测误差。水田环境具有的独特特征，增加了水田拖拉机下陷深度检测的难度。

本文基于惯导技术，实时检测了水田拖拉机行驶过程中的三维加速度和三维姿态角，基于欧拉角坐标系的变换，计算出某一时刻水田拖拉机实时的下陷深度。该方法是一种非接触式的测量与计算方法，不受水面扰动、水体泼溅、车体随意倾斜的影响，实验与计算结果显示，是一种稳定、有效、实时检测水田拖拉机下陷深度的方法。

1 检测方法

1.1 坐标系的建立

建立如图1 所示的坐标系。图中，在惯导安装的位置上设置惯导坐标系O-XYZ，为右手坐标系。其原点O位于惯导装置的几何中心；Y轴正向指前，即指向拖拉机向前运动方向；Z轴垂直地面正向指天；X轴正向垂直于YZ平面并指向拖拉机外侧。建立大地坐标系G-XYZ，同样为右手坐标系。大地坐标系G-XYZ的X、Y、Z轴分别与拖拉机静止时惯导坐标系O-XYZ的X、Y、Z轴方向平行；坐标系G-XYZ的Z轴垂直于大地表面。大地坐标系G-XYZ原点G位于地面上，大地坐标系G-XYZ原点G与惯导坐标系O-XYZ原点O之间的距离在大地坐标系G-XYZ的Z轴上的投影即为惯导相对地面的高度。

图1 惯导与下陷深度检测点的坐标系示意图Fig.1 Schematic diagram of coordinate system of inertial navigation and subsidence depth points

在拖拉机前进方向的右侧的行走系履带下部设置下陷深度检测点坐标系O'-X'Y'Z'，为便于测量和人眼直观辨识，将坐标系O'-X'Y'Z'原点O'设置在履带行走系中间的承重轮轴线中心上，坐标系O'-X'Y'Z'原点即下陷深度检测点。同理，在拖拉机前进方向的左侧的行走系履带下部设置下陷深度检测点坐标系O"-X"Y"Z"。拖拉机两侧运动方向即为拖拉机运动方向，因此坐标系O'-X'Y'Z'和坐标系O"-X"Y"Z"的X、Y、Z轴的正向均与坐标系O-XYZ的一致。

坐标系O'-X'Y'Z'原点O'在坐标系O-XYZ中的位置可表示为：=[x'，y'，z']T，坐标系O"-X"Y"Z"原点O"在坐标系O-XYZ中的位置可表示为：=[x"，y"，z"]。当拖拉机组装完毕后，拖拉机两侧履带相对主体的位置是固定不变的，即坐标系O'-X'Y'Z'原点O'在坐标系O-XYZ中的位置和坐标系O"-X"Y"Z"原点O"在坐标系O-XYZ中的位置是2 组和拖拉机几何尺寸相关的常数，其空间尺寸精度通过加工和装配公差来保证，且该位置参数值并不随拖拉机的运动而发生改变。

1.2 水田拖拉机三维姿态的表示

由于水田土壤烂滑的独特性，水田拖拉机行驶过程中时常会发生前后倾斜、左右倾斜，即其三维姿态时刻在发生变化，此时需要借助三位姿态角和坐标系变换的方法，将拖拉机行驶过程中其姿态相对大地坐标系的变化值表示出来。

如图2 所示，坐标系G-XYZ表示大地坐标系，坐标系O-XYZ表示拖拉机的初始静止位置0，坐标系O1-X1Y1Z1表示拖拉机行驶一段时间t后的位置1。

坐标系O-XYZ原点O在大地坐标系G-XYZ的Z轴上的投影点为OGZ，坐标系O1-X1Y1Z1原点O1在大地坐标系G-XYZ的Z轴上的投影点为OGZ1。坐标系O-XYZ的X、Y、Z轴与大地坐标系G-XYZ的X、Y、Z轴方向平行。平移坐标系O1-X1Y1Z1到其原点和大地坐标系G-XYZ原点重合的位置、且保持X、Y、Z三轴的方向不变后，得到坐标系O1'-X1'Y1'Z1'。

采用欧拉角表示转换矩阵的方法[9]，坐标系O1'-X1'Y1'Z1'的X1'、Y1'、Z1'三轴方向距大地坐标系G-XYZ的X、Y、Z轴的角度分别为：φ、θ、ψ，坐标系O1-X1Y1Z1的X1、Y1、Z1三轴的方向距大地坐标系G-XYZ的X、Y、Z轴的角度也分别为：φ、θ、ψ。

车体发生前后倾斜可视为车体绕大地坐标系G-XYZ的X轴旋转角度φ，该向余弦矩阵Rot（x1，φ）可表示为

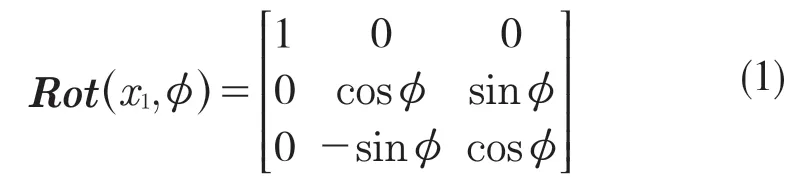
而车体发生左右倾斜可视为车体绕大地坐标系G-XYZ的Y轴旋转角度φ，该向余弦矩阵Rot（y1，φ）可表示为

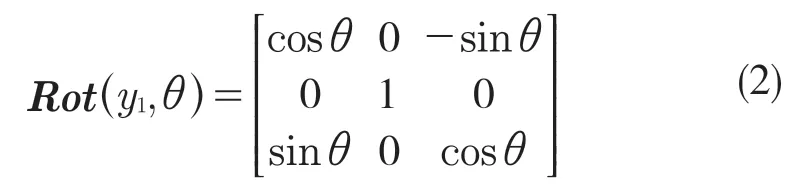
按先绕X轴再绕Y轴再绕Z轴的旋转顺序，此时水田拖拉机位置1 相对位置0 的坐标转换矩阵Rot（0，1）可表示为

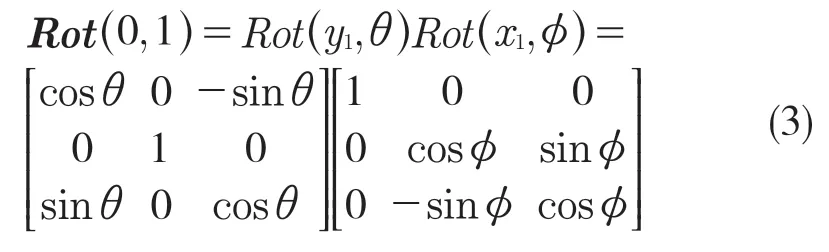
1.3 下限深度的计算

由于水田土壤烂滑的独特性，从实际操作中发现，水田拖拉机的下陷可分为两部分：一部分是车体整体呈直线上下的下陷；另一部分是车体发生前后倾斜或左右倾斜时，水田拖拉机行走系不同局部位置的不同深度的下陷。

如图2 所示，拖拉机行驶一段时间t后，车体整体的下陷深度可表示为水田拖拉机位置0 与位置1 的距离在大地坐标系G-XYZ的Z轴上的投影距离，即线段的长度，其可以通过与大地坐标系Z方向上垂直加速度的关系式求出。该关系式可表示为

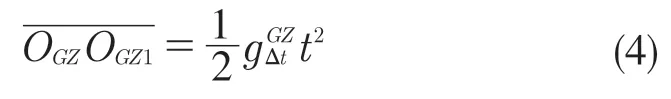
然而由于惯导装置是固定在拖拉机上，在行驶过程中，惯导装置和水田拖拉机的三维姿态一样时刻在发生变化。从惯导读取的加速度值是以其自身坐标系为基准，需要经过转换矩阵Rot（y1，φ）转化后，才能表示出大地坐标系Z方向上垂直加速度。垂直加速度的计算公式为

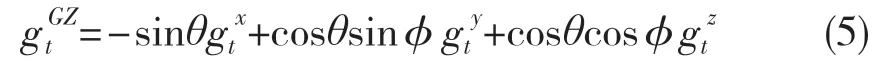
式中：gtx——沿惯导坐标系x轴测量的加速度分量；gty——沿惯导坐标系y轴测量的加速度分量；gtz——沿惯导坐标系z轴测量的加速度分量。

为具体地说明水田拖拉机车体发生前后倾斜或左右倾斜时，不同局部位置具有不同下陷深度的情况，对图1 中水田拖拉机行走系两侧下陷深度检测点的位置变化进行以下计算公式的推导。

此时处于位置1 的水田拖拉机的右侧的下陷深度检测点在坐标系O-XYZ下可表示为

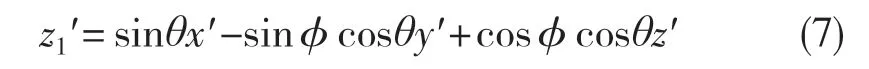
处于位置1 的水田拖拉机左侧的下陷深度检测点在坐标系O-XYZ下可表示为

则水田拖拉机行走系的右侧下陷深度为

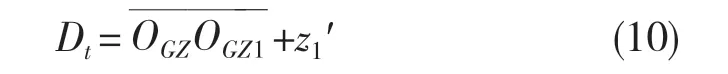
水田拖拉机行走系的左侧下陷深度为

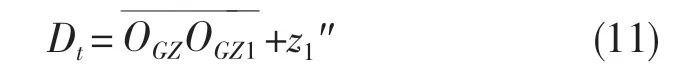
1.3 PLC 程序

PLC 具有可靠性高、抗干扰能力强、易于扩展、寄存器和计数器数量巨大等特点，适用于构建采集、通讯、计算、存储下陷深度检测数据的主要电气系统[10-11]。

系统程序采用ispsoft-DELTA IA-PLC 语言进行编写[10-11]，在梯形图程序中通过 PLC 功能函数接收惯导发出的测量值信号，实现下陷深度测量值的自动采集、通讯、计算和存储，PLC 控制的技术特点保证了本检测系统的可控制性能、抗干扰能力及自动化程度等。

图3 为在某一时刻t采集惯导发送的在其自身坐标系下X方向上加速度值的PLC 梯形图，采集Y方向上加速度值和Z方向上加速度值的PLC 梯形图与之类似。图4 为采集惯导发送的三维姿态角的PLC 梯形图。其中，D 脚标700 表示航向角数据的采集，D 脚标702 表示俯仰角数据的采集，D脚标704 表示横滚角数据的采集。航向角表示车体绕坐标系O-XYZ的Z轴旋转角度ψ，俯仰角表示车体绕坐标系O-XYZ的X轴旋转角度φ，横滚角表示车体绕坐标系O-XYZ的Y轴旋转角度θ。

图3 采集X 方向上加速度值的PLC 梯形图Fig.3 PLC ladder diagram for collecting acceleration value in X direction

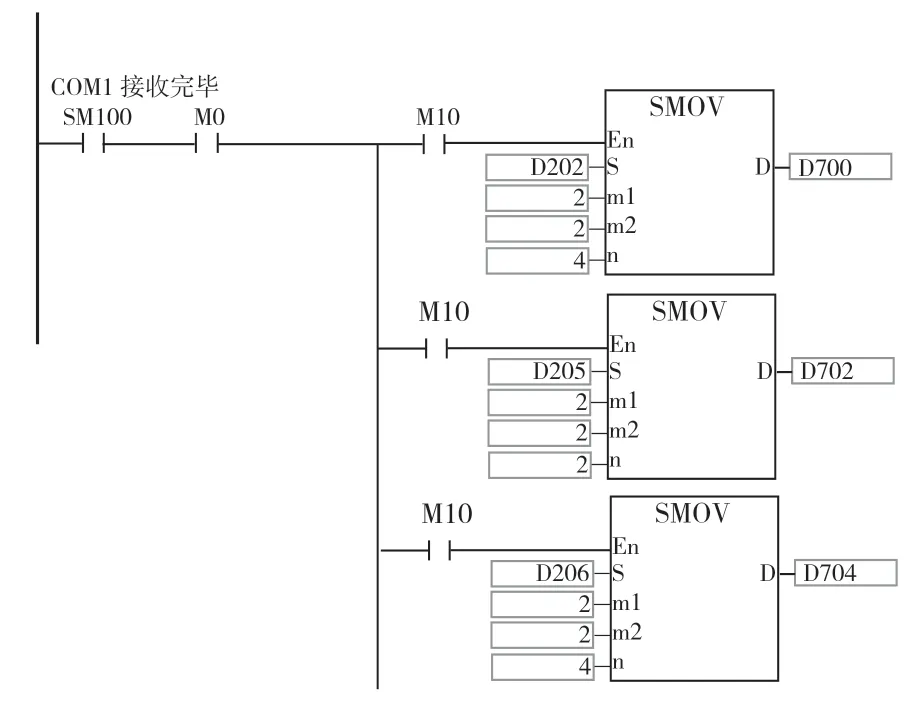
图4 采集三维姿态角的PLC 梯形图Fig.4 PLC ladder diagram of collecting 3D attitude angle

本系统采用开环控制的方式读取各传感器采集的数据。采用开环控制方式最大的优点是无反馈环节，即输出量C（s）受控于输入量R（s），且不能对控制量反施影响。

采集到惯导发送的加速度值和旋转角度φ和旋转角度θ，利用PLC 内嵌的st 语言编写功能块，计算沿大地坐标系Z方向上垂直加速度，并计算水田拖拉机车体发生倾斜时拖拉机行走系各不同局部检测点的下陷深度。部分程序代码如图5 所示。

图5 计算下陷深度的st 语言程序Fig.5 st language programs for calculating subsidence depth

程序中设置屏蔽段的原因是由于受到地球运转和惯导加工工艺与检测原理的影响，即使放置在人眼视为静止的地面，惯导输出的读数仍然是持续小范围变化的值，而不是一个静止的常数值。数值波动会被错误地认为是合理的沿大地坐标系Z轴的下陷引起的加速度变化，从而会对整体下陷深度的测量产生误差。本文采用设置屏蔽段上下区间值的方法，将有可能产生检测误差的细小波动值舍去。

2 实验与分析

将惯导安装在某型拖拉机上开展实际测试，车身高度2.556 m。设置3 种地形特征：（1）台阶式下沉地面；（2）台阶式上升地面，台阶高度2 mm；（3）斜坡式上升地面，斜坡角度19.35°，高度0.27 m。根据惯导输出的三维加速度值和三位姿态角，按式（4）—式（11）依次计算和记录在3 种地形上行驶时车体高度的实时变化曲线，如图6—图8 所示。曲线是计算左右侧下限深度变化曲线的重要中间参数。为了便于与地面高度形成直观的比较，图中实际计算数据已减去车体高度。实验中，车速设为8 km/h，惯导数据采样间隔0.1 s。

如图6—图8 所示，细实线表示实际地面值，带星号的细实线为未加屏蔽段计算的车体高度值，带圆圈的细实线表示在程序中增加屏蔽段和合理设置屏蔽段上下区间值后计算的车体高度值。图6 中细实线表示一半为地面一半为下沉2 mm 地面的台阶式下沉地面，下沉在拖拉机前进方向1 m 处。图7 中细实线表示一半为地面一半为上升2 mm 地面的台阶式上升地面，上升在拖拉机前进方向1 m 处。图8 中细实线表示角度为斜角19.35°高度0.7 m 的斜坡式上升地面。

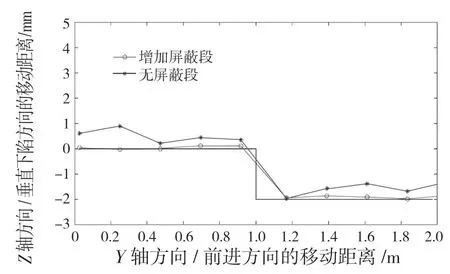
图6 台阶式下沉地面行驶时车体高度的变化曲线示意图Fig.6 Variation curve of tractor body height when driving on stepped sinking ground

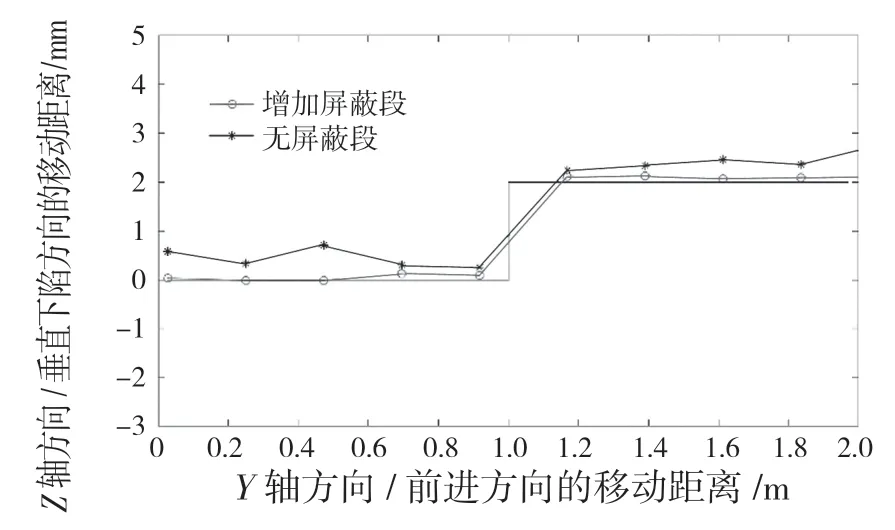
图7 台阶式上升地面行驶时车体高度的变化曲线示意图Fig.7 Variation curve of tractor body height when driving on stepped up ground

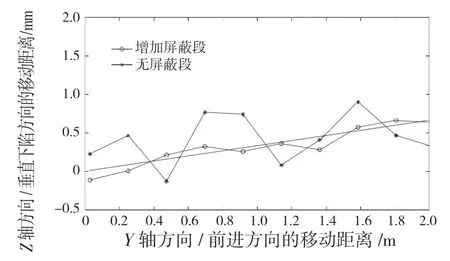
图8 斜坡式上升地面行驶时车体高度的变化曲线示意图Fig.8 Variation curve of tractor body height when driving on sloping rising ground

如图6—图8 所示，在地面情况变化不大的情况下，如水平路面和斜角19.35°高度0.7 m 缓慢上升的斜坡式上升地面，未加屏蔽段计算的车体高度值偏离细实线所标识的实际地面值较大，增加了累计误差，甚至会出现严重失真的情况。增加屏蔽段计算的车体高度值偏离细实线所标识的实际地面值较小，同时也较为稳定。

此外，在经过台阶式下沉或上升明显的地面，由于此时沿大地坐标系Z轴的加速度作用时间相对较长，垂直方向的位置落差较明显，采用增加屏蔽段和未加屏蔽段的计算方法计算出车体高度值均在有效范围内。

3 结论

本文基于惯导技术提出了一种间接的、不接触水面实时检测拖拉机行驶过程中下陷深度的方法，避免了水体和烂泥对检测精度的影响。

（1）计算下陷深度的关键参数是计算垂直方向的加速度，基于欧拉角推导的拖拉机静止和移动位置之间相互表示的转换矩阵，是将从惯导读取的基于其自身坐标系的加速度转化为计算垂直方向的加速度的关键。

（2）PLC 作为构建采集、通讯、计算、存储下陷深度检测数据的主要电气系统，具有结构简单、运行稳定可靠等优点，大幅度降低了检测过程所需的时间和人力。

（3）实验结果表明，通过设置屏蔽段上下区间的值，有助于稳定检测。此外，拖拉机行走系不同位置的下陷深度是不一样的。