应用于换热网络优化的并行双层RWCE算法

2022-10-30刘洪彬崔国民周志强肖媛张冠华杨其国

化工进展 2022年10期

刘洪彬，崔国民，周志强，肖媛，张冠华，杨其国

（1 上海理工大学能源与动力工程学院，上海 200093；2 上海市动力工程多相流动与传热重点实验室，上海 200093）

换热网络优化是过程工业节能的重要途径，可为企业提供显著的节能效果和经济效益。换热网络优化属于混合整数非线性规划模型（mixedinteger nonlinear programming，MINLP），具有严重的非凸性、非线性和不连续性，求解极为困难。目前，换热网络问题的求解方法主要分为夹点技术法和数学规划法。夹点技术法是基于热力学原则提出的优化方法，具有简单实用的特点，但受限于变量维数，难以应对大型换热网络问题的优化需求。随着计算机技术和优化方法的发展，数学规划法在求解复杂的换热网络问题中备受关注。

启发式算法因具有强鲁棒性和易操作性的优点，已逐步成为换热网络的主要优化方法。过去，如遗传算法（GA）、粒子群算法（PSO）、模拟退火算法（SA）等经典启发式算法应用于换热网络综合并表现出巨大的潜力。近年来，为应对换热网络优化需求，提升优化质量和效率，许多学者开发了混合算法、双层算法及并行算法。Pavão等提出了SA-RFO 混合算法，采用SA 算法和火箭尾焰优化算法（rocket fireworks optimization，RFO）同步优化整型变量和连续变量，提高了大型网络的优化效率。刘凯等提出一种双层优化算法，采用Alopex 进化算法（Alopex evaluation algorithm，AEA）优化结构的分流比，PSO 算法优化换热量，通过分离变量提高结构组合变异能力，同时结合不可行解修复策略提高算法局部搜索能力。Aguitoni等提出的双层算法，其中SA 算法提供网络拓补，差分进化算法（DE）则在固定结构上优化连续型变量，取得良好效果。Santos 等则提出一种双层算法，其中外层使用SA 算法优化整型变量而内层使用PSO算法优化连续变量，并基于一种减少决策变量的新模型，有效降低了优化难度。为提高求解效率，康丽霞等提出了CPU+GPU 异构系统下的并行GA算法，大幅降低了求解时间，但未应用于大型换热网络。姜楠等提出了并行BB/SQP 混合算法，其中利用分支定界算法（BB）筛选可行结构，采用序贯二次规划算法（SQP）对初始结构进行非线性规划，并结合GPU 并行计算获得了显著加速效果。Pavão等将一种GA/PSO混合算法并行化处理，极大提高了个体单次迭代速度。周志强等则提出了RWCE-GA 混合算法，其中强制进化随机游走算法（RWCE）进行同步优化，GA 算法则周期性杂交个体增强整型变量搜索能力，结合多核并行计算，提高了算法优化质量和效率。

强制进化随机游走算法（RWCE）是肖媛等提出的一种新型启发式算法，种群间无信息交流，独特的接受差解机制可跳出局部陷阱，具有极强的全局搜索能力，避免了算法过早收敛问题。但RWCE算法在保证全局搜索能力时，难以兼顾局部搜索。算法因接受差解而难以搜索到局部最小极值点，存在差解代替优解情况。为弥补这一缺陷，肖媛提出了一种精细搜索的后处理方法，将获得的固定结构再次精细搜索。该策略提高了算法局部领域的搜索精度，但未能解决优化过程优解被替代问题。因此鲍中凯等提出一种结构保护策略，通过建立对应的平行种群接收过程结构并实时精细搜索，保护了过程优解，但因平行种群消耗了计算机算力而严重限制源种群规模，削弱了算法全局搜索能力。

基于此，为平衡算法的全局与局部优化能力并降低大型换热网络优化时间，本文提出并行双层RWCE 算法。算法基于OpenMP 并行技术，通过分配线程构建层级关系，其中基础层保持强悍的全局优化能力，精细层则采用精细搜索策略提高算法的局部搜索能力。最后，优化2个大型换热网络算例进行验证，结果表明并行双层RWCE 算法提高了局部搜索精度，保护了过程潜在优解，同时在并行计算加持下，全局搜索能力也大幅提高。

1 换热网络数学模型

本文基于节点非结构（node-wise nonstructural superstructure，NW-NSS）模型优化换热网络，模型初始化时为空节点网络，冷热流股呈逆流布置，各流股节点数量、分流分支数及分支上节点数均可自主预设。模型结构如图1 所示，具有2热流股和2条冷流股，分别以和表示；冷热流股上设有3 主节点，分别用和表示；冷流股上3 支分流和热流股2 支分流，分别以和表示。换热器由冷热流股上的空节点随机匹配连接形成，图中有4个换热器，如连接的实心点所示；冷公用工程和热公用工程处于流股末端，以调节未到达目标温度的流股。换热器节点匹配关系和换热量的随机游走实现换热网络的全局优化。

图1 模型

1.1 目标函数

该模型以年综合费用（total annual cost，TAC）最小为优化目标，目标函数如式(1)。其中前3项为换热器和公用工程设备的固定投资费用、面积费用；后两项为冷热公用工程能源消耗费用。

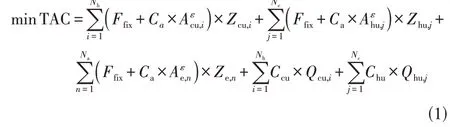
式中，、分别为热、冷流体股数；为流股总节点数；为0-1 变量，值为1 时表示该节点上存在换热器或冷热公用工程，值为0时表示为空节点；为固定投资费用；为面积费用系数；为面积费用指数；、为冷、热公用工程的运行费用系数；、、为换热器和冷热公用工程的面积；、为冷热公用工程热量消耗量。

换热面积计算如式(2)。

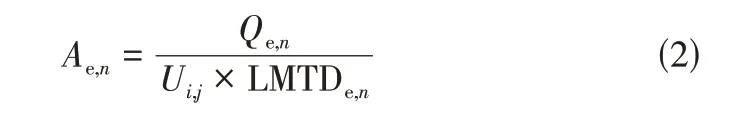
式中，为换热器总传热系数；LMTD 为对数平均温差。

1.2 相关约束

流股热平衡如式(3)、式(4)所示。

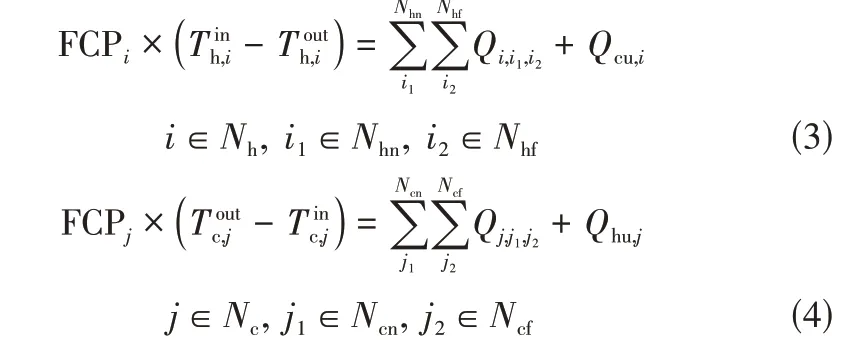
式中，和分别为热流股和冷流股温度；in和out代表流股上节点的进口和出口温度；和分别代表冷热流股的主节点数；和分别代表冷热流股分流数。

换热器及公用工程热平衡如式(5)～式(8)所示。

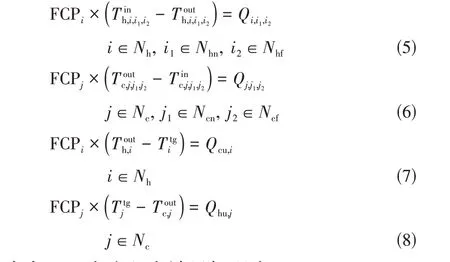
式中，为流股末端目标温度。

分流汇合温度约束如式(9)、式(10)所示。

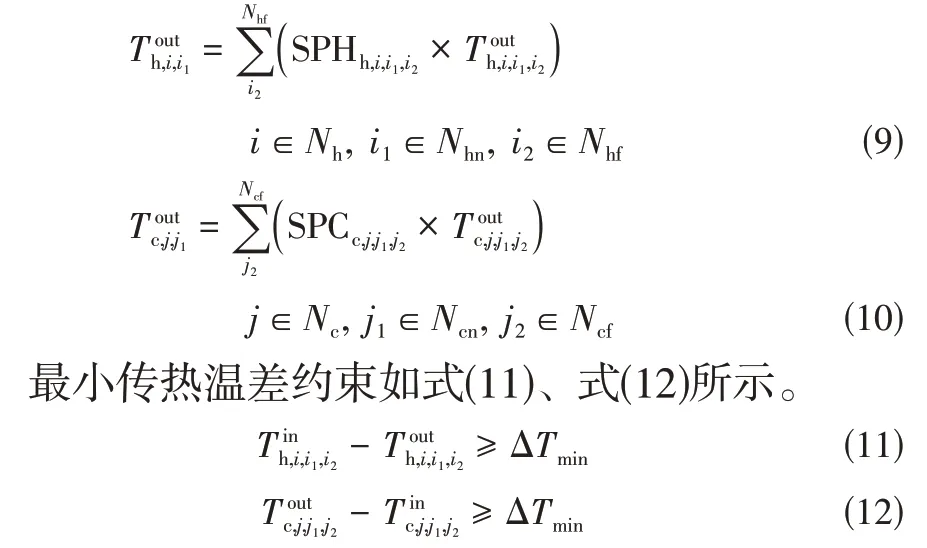
式中，Δ为最小传热温差。在追求最小年综合费用时，目标函数的换热面积费用作为隐含约束，杜绝了换热面积无限大等不合理情况，同时为更好与其他文献优化结果对比。因此文中最小传热温差设定为0℃，旨在于拓宽算法的搜索路径，实际上优解均不会出现过小温差，优化时出现违反温差约束则采用惩罚函数进行纠偏。

2 并行双层RWCE算法

2.1 基础算法及不足

RWCE 算法是肖媛等提出的新型启发式算法，割裂种群间个体信息交流以保持种群多样性，独特的接受差解机制可有效跳出局部极值陷阱，对于高度非凸非线性的换热网络优化难题具有极强的全局搜索能力。应用于换热网络时，算法详细步骤见下文2.3节，基础RWCE算法流程如图2所示。

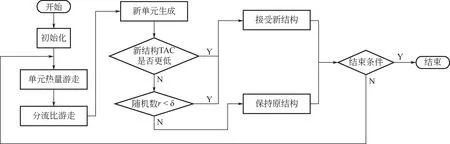
图2 基础RWCE算法流程

图2 中以随机数决定是否接受新结构这一步骤，是基础RWCE 算法的接受差解机制，是跳脱局部陷阱的关键，可有效提高算法的全局搜索能力。也正因如此，该机制在局部领域搜索时，难以搜寻到最小极值点。在具有众多极值的解空间内，基础算法搜寻到的解均与其领域内的极值点存在一定差距。因此，算法最后得到的解不一定为该解空间的最小极值，存在最小极值被替代的现象。换热网络规模越大，极值点越多，则越容易出现差解代替优解的现象。

基础算法因局部搜索精度低造成了该不良现象，增强局部搜索能力则可有效避免。若为了提高局部搜索精度，简单地降低接受差解概率或减小游走步长，则破坏了全局搜索能力，易致使算法早熟收敛。因此，最佳方案是建立另一层算法，持续对基础算法的当前解进行精细搜索，既保持了基础算法的强全局搜索能力，又能提高搜索精度，避免优解被替代。但另一方面，换热网络优化时间随问题规模增大而急速增加，一些大型换热网络算例因优化时间长而严重限制了算法的种群数量，致使算法的全局搜索能力大幅削弱。若简单地建立双层算法，会额外消耗算力再度降低算法全局搜索能力，导致全局与局部搜索能力失衡加剧。

基于上述分析，本文提出一种并行双层RWCE算法。一方面基于多核并行技术，极大增加初始种群基数，降低优化时间。另一方面，根据该技术特点，通过线程分配构建双层算法，不干扰基础算法强大的全局搜索能力的情况下提升局部搜索能力，同时可根据需求调整线程分配，平衡算法全局与局部搜索能力。

2.2 多核并行OpenMP技术

采用Fortran+OpenMP并行编程模型实现算法并行化。OpenMP 是基于线程共享内存体系的并行编程模型（图3）。对于多核计算机而言，单个CPU核心可包含一或多个线程，并行时可将计算机内存划分为所有线程可访问和仅特定线程可访问的共享存储空间和私有存储空间，以此进行线程间的信息互通与保护。基于OpenMP模型的程序运行时采用的是Fork-Join并行执行方式，如图4所示。当程序开始时只有主线程进行串行计算，进入并行域后则开辟其他线程共同执行域内任务，离开并行域后则只保留主线程串行运行。

图3 内存共享模型

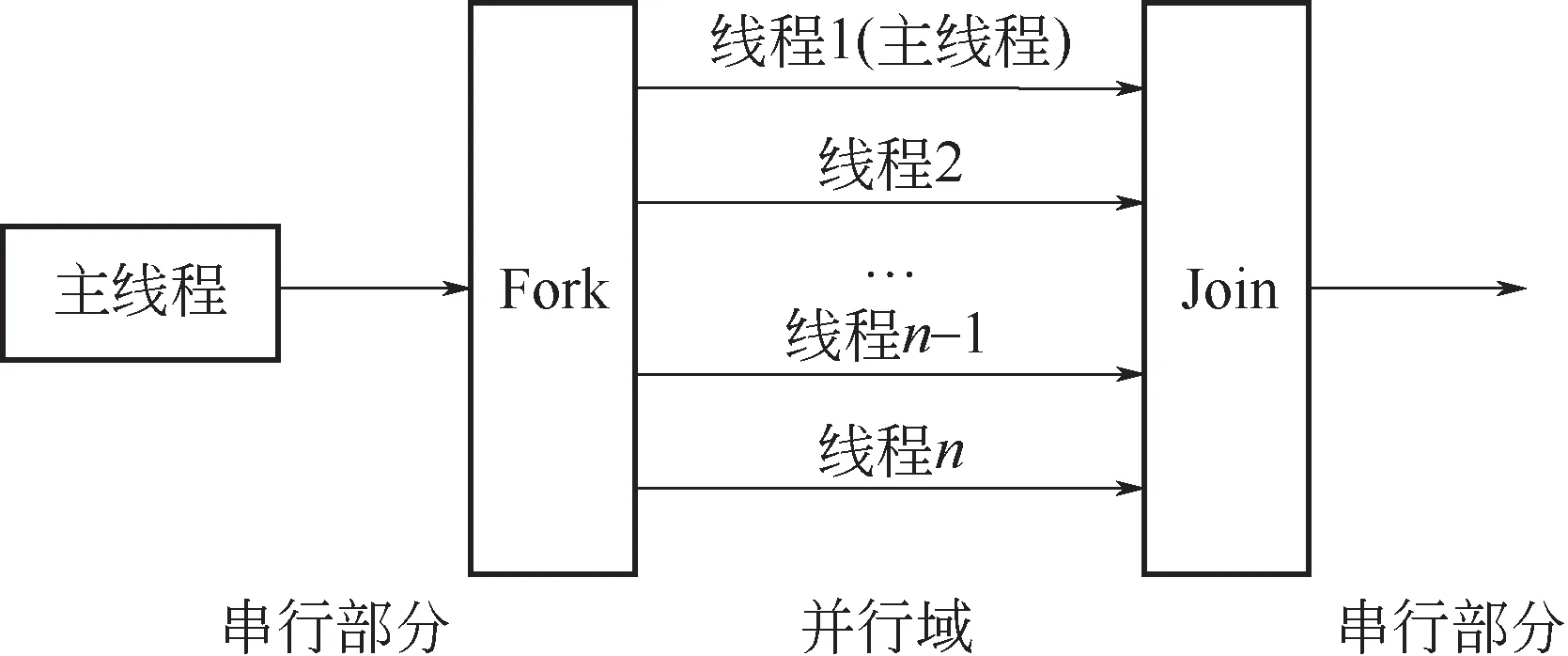
图4 OpenMP程序并行执行方式

2.3 并行双层RWCE算法

2.3.1 层级关系

并行双层RWCE 算法分为基础层和精细层，基础层与精细层分属不同线程，均开辟各自私有变量存储空间，避免线程变量冲突。精细层从属于基础层，两层间通过共享变量建立信息单向传递通道，当基础层更新最优解时向精细层传递结构信息，精细层对该结构精细搜索并记录当前最优解和历史最优解。

大型换热网络解空间内遍布二元变量和连续型变量的局部陷阱，若算法缺乏全局搜索能力则易导致早熟收敛。肖媛和鲍中凯等均证实换热网络解的优良程度主要取决于全局寻优能力。算法可根据全局与局部搜索需求自主分配线程，本文中精细层分配一个线程，剩余线程全部分配给基础层以增大种群规模。基础层以全局搜索能力为主，在全局范围内搜寻费用最低的解空间，当基础层搜寻到费用更低的解则传递给精细层。精细层则对该解的局部领域进行高精度的精细搜索，以局部解空间的最小极值点为目标。基础层与精细层能力互补，相互配合平衡全局与局部搜索，并行双层RWCE 算法流程如图5所示。

图5 并行双层RWCE算法流程

2.3.2 基础层

基础层为基础RWCE 算法，并设置较大的游走步长和接受差解概率，保持强劲的全局搜索能力。算法主要流程不变，增设一信息单向传递环节。当基础层更新其最优解时，将其传递给精细层进行精细搜索。主要步骤如下。

Step1：种群初始化。随机产生个初始种群，各种群内有个体，个体起始状态为空网络结构。

Step2：随机游走阶段。个体以一定概率对现有换热单元热负荷或分流比SPH、SPC任一变量进行游走。当任一变量小于阈值时消除该换热器。如式(13)。

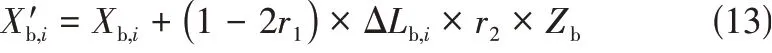
式中，、为在(0,1)均匀分布的随机数；为判断是否执行的0-1变量；Δ为最大游走步长。

Step3：新单元生成阶段。个体以一定概率在冷热流股空节点上形成新单元，并赋予新单元初始换热量、冷热流股上的分流比。如式(14)～式(16)。

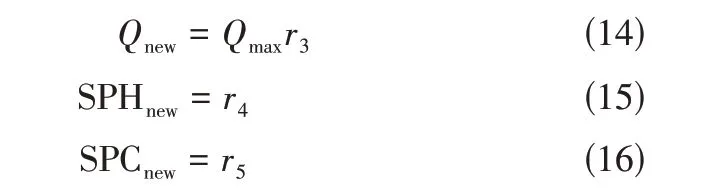
冷热流股的初始分流比由随机数给定，因此各分支分流比之和可能不为1，在计算时需归一化处理。以热流股为例，如式(17)。

式中，、、为(0,1)均匀分布的随机数；为最大初始热量。

Step4：选择与变异阶段。个体游走后成为新的状态点，此时以TAC 作为评判指标，费用降低则选择此状态作为下一次迭代的起点；若费用反而升高，则返回游走前原状态点，或者以一定概率接受该状态点继续迭代。如式(18)。

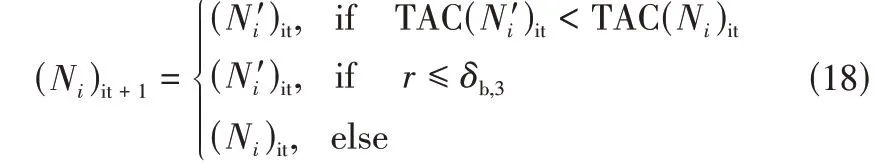
式中，和′分别为游走前后的状态点；为游走变量；为接受差解概率；it为迭代次数。

Step5：结束条件。当满足迭代步数时结束程序，否则返回Step2继续迭代。

2.3.3 精细层

精细层沿用RWCE 算法，但不产生初始结构，当基础层最优解更新时则接收结构信息并进行精细搜索，主要步骤如下。

Step1：种群初始化。由于仅单线程工作，因此只有单种群个体。采用发散搜索策略，将接收的结构或精细层自身结构赋值给所有个体，利用RWCE算法个体独立进化特点，使各个体初始点发散分布在局部领域范围内，更快搜索到最小极值点。

Step2：随机游走阶段。相对于基础层，精细层采用降维搜索策略。游走步长较基础层缩小1～2个量级，并以换热单元数量为指标降低决策变量游走频率，游走时选择部分换热单元中、SPH和SPC 任一变量，减少变量间同步优化引起的干扰，提高局部搜索精度，如式(19)、式(20)。

式中，为当前结构换热器数量；为精细层优化变量；Δ为精细层游走步长；为0-1 为变量。

Step3：换热单元生成阶段。操作同基础层，但新单元的生成概率和数量需大幅降低，避免对结构造成频繁干扰，阻碍优化进程。

Step4：选择与接受差解阶段。操作同基础层，但接受差解概率较基础层大幅降低。

Step5：终止条件判断。当种群最优个体费用在一定迭代步内降幅小于设定值时终止精细搜索程序；否则，返回Step2 继续迭代，或定周期筛选精细层最优解返回Step1再循环。

3 算法效能探究

算法采用Fortran 编程，计算机操作系统为Windws10，CPU 为Intel(R) Xeon(R) Gold 6226R@2.90GHz（2处理器），最大核心数为32核，CPU可处理超线程运算。

现优化H6C10算例验证并行双层RWCE算法的优化性能，该算例包含6热流股和10冷流股。节点非结构模型参数设置如下：冷热流股上10 个主节点，冷热流股分别设3 和8 分流，分流上均设1个节点。并行双层RWCE算法仅启用最低2线程测试基本性能，分别为基础层和精细层。基础层参数：基础层共5 个体，换热量游走步长1500kW，初始生成热量2000kW，换热单元生成概率0.2，接受差解概率0.01；精细层参数：精细层共20个体，换热量游走步长5kW，初始生成热量25kW，换热单元生成概率0.01，接受差解概率0.0001，千万步内TAC 降幅小于0.02%时终止。其优化结果如图6所示。

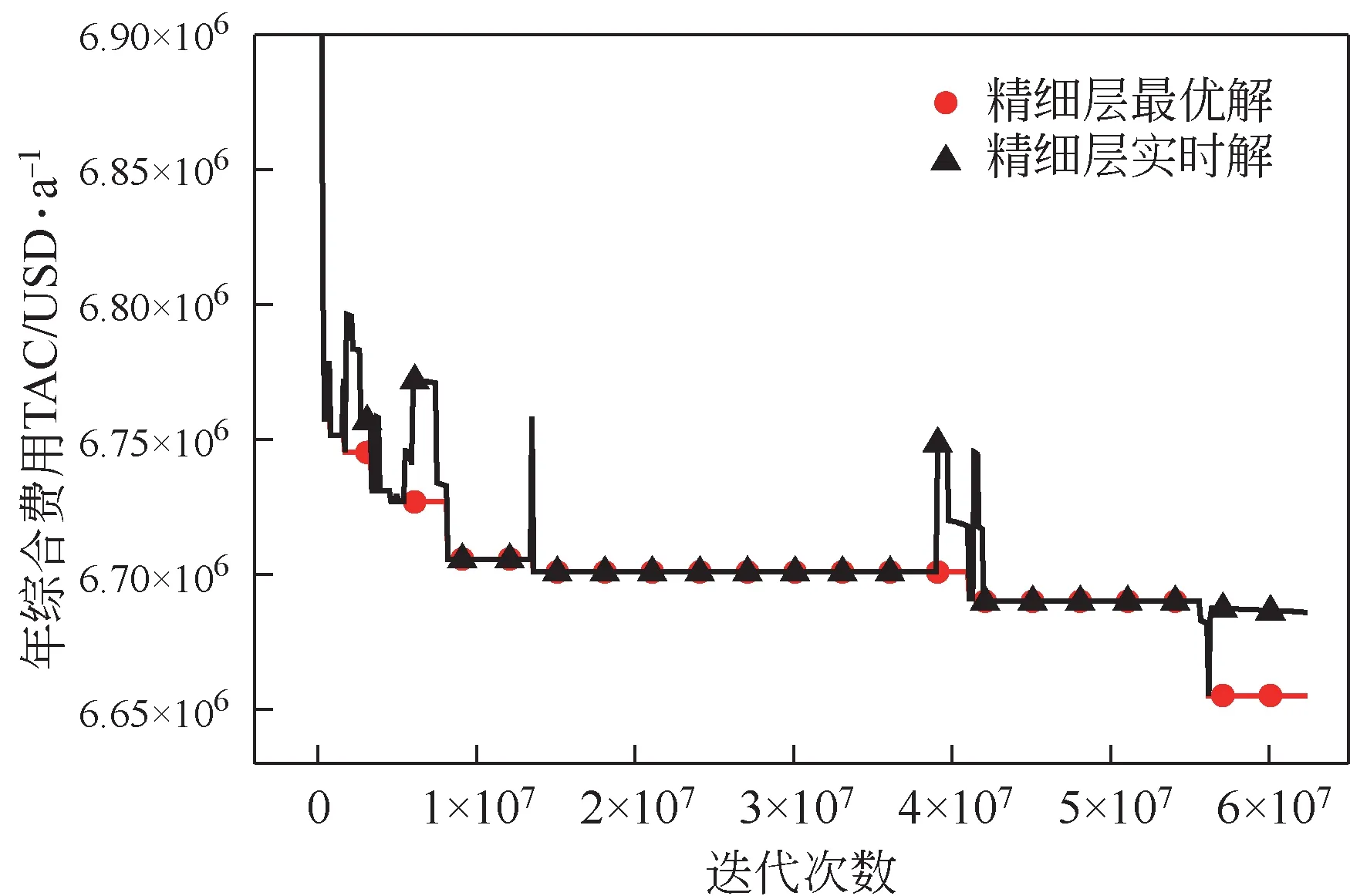
图6 精细层最优费用和实时费用下降曲线

优化时基础层将所有过程最优解传递给精细层精细搜索，因此精细层的解中包含当前优化的实时精细解及记录的历史最优解。观察图6发现，精细层实时解多次出现费用上升的情况。即基础层看似找到了费用更低的新解，但实际交由精细层精细搜索后发现较前一解费用更高，反映为优解被差解替代现象。如5.62×10步更新后的实时精细解6686047USD/a 高于6655243USD/a 的最优精细解，虽然两个结果均优于绝大部分文献，但这种现象却是基础层的异常现象，若无精细层则会导致上述差解替代优解的情况。正如图6所示，精细层起到了保护优解的作用。

加速比是考究并行计算的重要指标，加速比为相同计算量下并行运算时间与串行运算时间的比值，加速比越接近启用线程数则算法加速效率越高，加速比越大则程序加速性能越好。现优化H6C10 算例，保持相同参数设置，对并行双层RWCE算法加速性能进行探究。并行双层RWCE算法分别开辟5、10、15、20、25、30个线程，每个线程优化1个个体。串行计算的基础RWCE算法则相应优化同等总个体数，分别是5、10、15、20、25、30 个个体。经过测试得，不同总个体数下每十万次迭代的运行时间及加速比如图7所示。

图7 串并行运行时间和加速比

由图7可看出，在相同的个体总数下，相较于串行计算，并行运行时间极短，计算时间都下降了1个量级，极大降低优化时间成本。加速比随着并行计算开辟的线程数呈先增后减趋势，当启用的线程数较少时，加速比接近于线程数，效率高；但随着启用线程数增加，加速比增长减缓甚至倒退。呈现该现象主要原因是线程开辟越多越逼近计算机性能极限，导致并行运算时间增加，使加速比增幅减缓。因此，在计算机有算力盈余情况下，并行计算加速比随线程数增加而增加，但加速效率随线程数增加而降低。运算时间较串行计算大幅降低，可增大算法的种群数量从而提升全局搜索能力。

综上所述，并行双层RWCE 算法因种群规模扩大而具有更强的全局搜索能力，且获得了高精度的局部搜索能力，解决了原算法差解代替优解的问题。

4 算例验证

4.1 算例1

20SP含有10股热流体和10股冷流体，是大型换热网络的通用算例之一，具体参数详见源文献。换热器和冷热公用工程费用计算公式为8000+800(USD/a)，冷热公用工程能耗费用分别为10USD·(kW/a)和70USD·(kW/a)。

采用并行双层RWCE 算法优化该算例，模型参数：网络设置10个主节点，3分流数，分流上1节点。算法参数如下，基础层分配60 线程而精细层1 线程，共启用61 线程。基础层参数：共1200优化个体，换热量游走步长100kW，初始生成热量150kW，换热单元生成概率0.2，接受差解概率0.01；精细层参数：共10优化个体，换热量游走步长5kW，初始生成热量25kW，换热单元生成概率0.01，接受差解概率0.0001。

并行双层RWCE 算法优化程序运行时间共17812s，加速比为26.0，精细层得到最优解为1717405USD/a。表1 中文献[22]采用遗传模拟退火算法，获得有分流的结果为1827772USD/a，运行时间为2786s，本文在相同时间的结果为1726858USD/a；文献[23]采用一种混合遗传算法获得最优结果为1753271USD/a，优化时间为2460s，本文在相同时间的结果为1727940USD/a；文献[24]建立了一种随机摄动机制，对换热单元的随机增减促进网络结构变异，获得结果1739079USD/a；文献[25]采用落后个体更新策略，引导落后个体进化，加强了个体间的竞争，获得结果为1730674USD/a；文献[26]为解决换热单元固定投资费用阻碍网络结构变异问题，提出一种固定投资松弛策略，其结果为1726399USD/a。

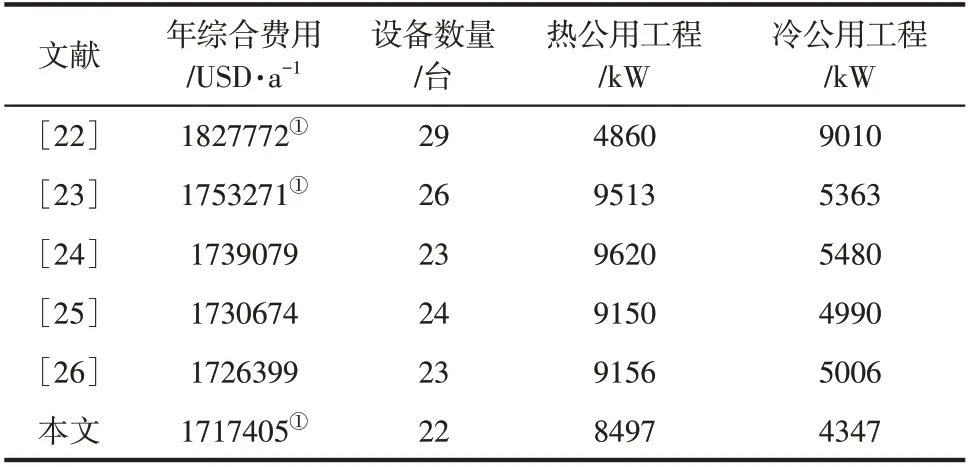
表1 算例1优化结果与文献结果对比

图8 为算例1 网络结构，其中传热温差最小的换热器是H10 热流股上第1 个单元，为14.47℃，符合实际情况。本文结构与文献[26]的结构相比，换热器数量多1 个共13 个、加热器减少2 个共4个，冷却器数量相同，但热源和冷源的消耗量均减少了659.9kW。虽然换热器的投资费用高出51726USD/a，但形成的结构更好回收了更多热能，减少了公用工程投资和能耗费用共60720USD/a，使总费用降低了8994USD/a。本文结构换热器更多，耦合关系更复杂，但年综合费用更低，证明并行双层算法的搜索能力更强。

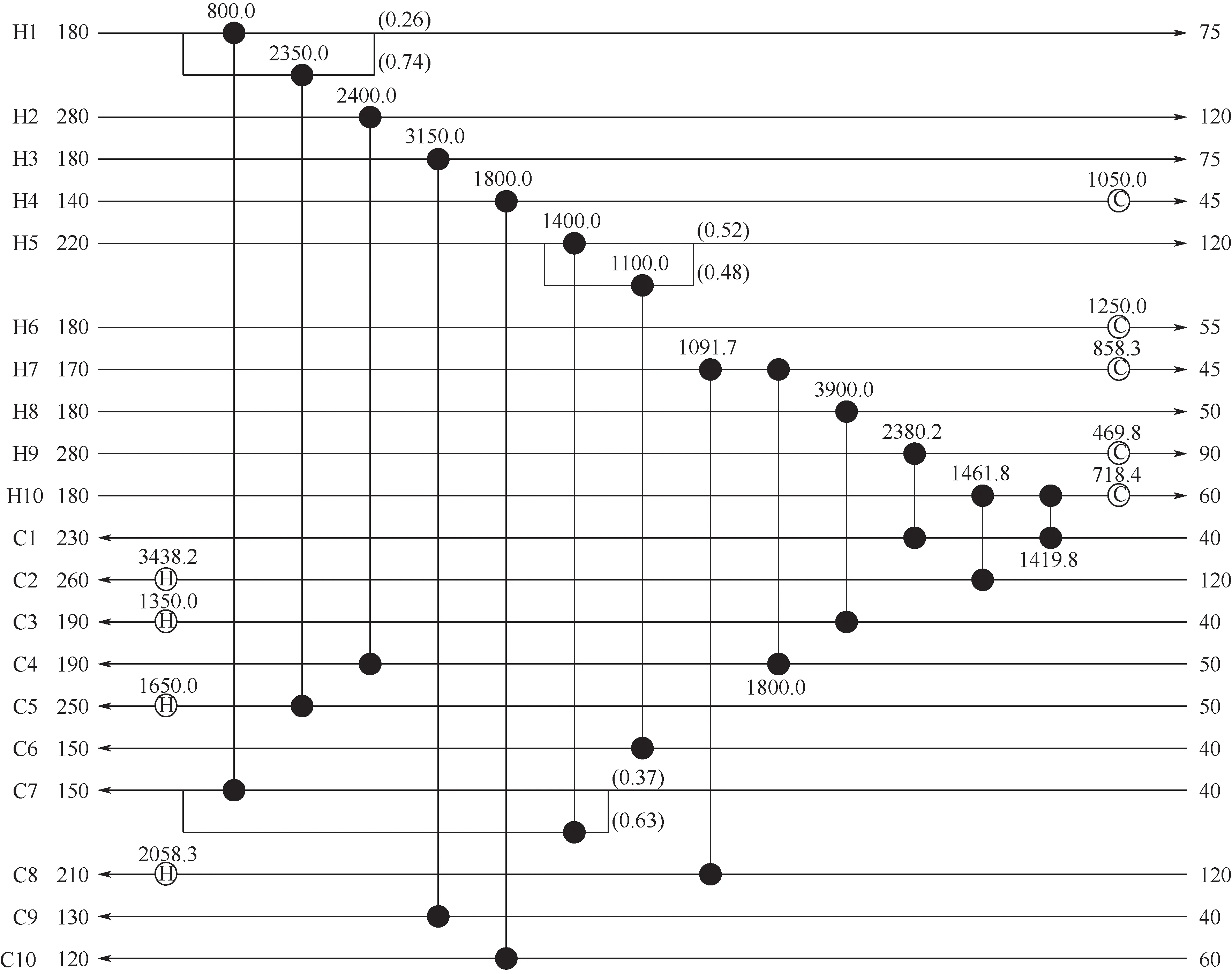
图8 算例1对应网络结构

4.2 算例2

39SP包含22 股热流体和17 股冷流体，是目前网络规模最大的通用算例，流股参数可参考源文献。换热器和冷热公用工程费用计算公式为8000+800(USD/a)，冷热公用工程能耗费用分别为10USD·(kW/a)和70USD·(kW/a)。该算例在优化时，因网络规模和结构复杂性导致计算量指数性增长，优化时间十分长，即便是基于节点非结构模型，串行计算时其优化个体数往往少于5个。对于十分依赖种群规模的RWCE 算法，时间成本极大限制了优化个体数，严重抑制了全局搜索能力。同时也因为该算例存在众多结构，极值点更是星罗棋布，差解代替优解现象更为频繁，对于高精度的局部搜索能力需要更加紧迫。

优化该算例时，模型参数：网络设置5个主节点，冷热流股分别为2 和3 分流，分流上1 节点。并行双层RWCE 算法参数如下，基础层分配60 线程而精细层1线程，共启用61线程。基础层参数：共600个体，换热量游走步长120kW，初始生成热量150kW，换热单元生成概率0.2，接受差解概率0.01；精细层参数：共5 个体，换热量游走步长5kW，初始生成热量25kW，换热单元生成概率0.01，接受差解概率0.0001。优化时算法基础层个体总数高达600个，远超串行计算种群规模，全局搜索能力得到大幅提升。现对比串行RWCE 算法与并行双层RWCE 算法的TAC 下降曲线，探究其优化性能。

如图9，在相同迭代步数内，并行双层RWCE算法的基础层最优解为1895715USD/a 远优于串行计算的原RWCE 算法获得的1925005USD/a，而且优化全程都处于大幅领先地位，再次佐证并行双层算法基础层具备更强的全局搜索能力。如前文所述，RWCE算法个体独立进化，种群规模是影响全局搜索能力的重要因素，通过并行技术在优化大型换热网络时可大幅增加种群规模，在相同优化时间内可获得更优的解。

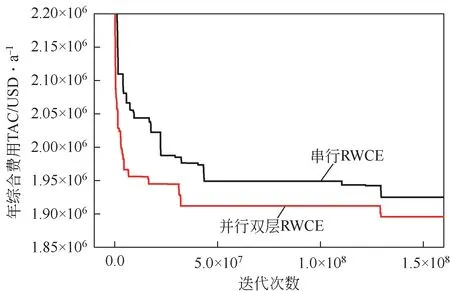
图9 并行双层算法基础层与原算法串行的性能比较

图10 中为精细层实时解与最优解的对比，可反映基础层差解代替优解的现象，由精细层记录。图中精细层一直存在实时解高于最优解费用的现象，如5×10步时TAC为1894191USD/a覆盖了TAC为1886613USD/a。这种现象由于基础层误判最小极值点而将差解替代了优解，表明基础层的搜索精度不足。但增加精细层可准确搜索到最小极值点并加以保护，避免被差解覆盖。对比图6和图10可发现，H22C17 较H6C10 算例基础层差解代替现象更为严重。由此可知，网络规模越大，基础层差解代替优解的异常现象越频繁，精细层则越显重要。

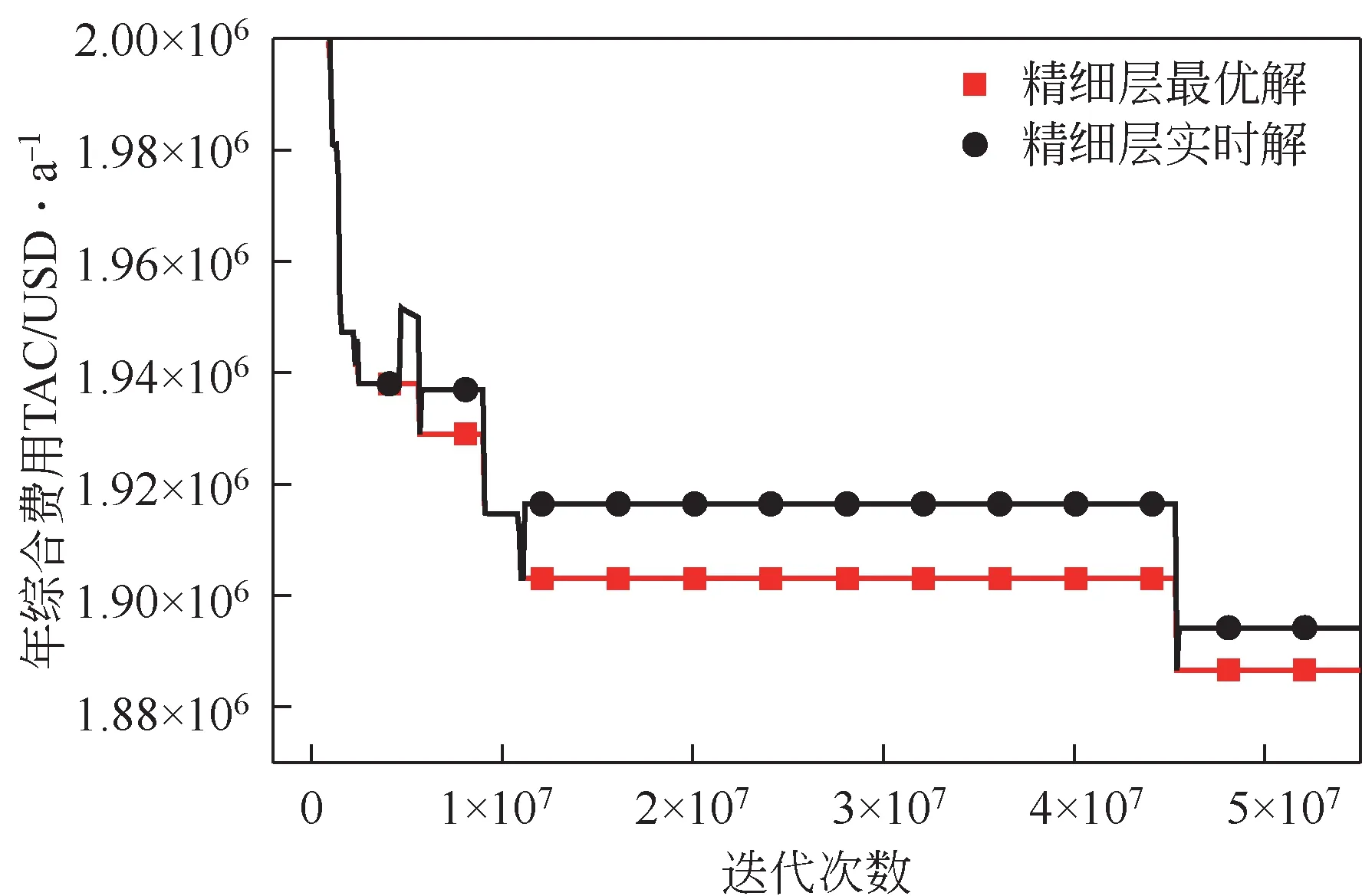
图10 精细层实时费用于最优费用曲线

精细层最优结果为1886613USD/a，耗时34071s，加速比为26.6，文献结果对比见表2，网络结构如图11 所示。39SP 算例目前的最优结果由文献[32]保持，采用子网络重组策略和公用工程重置策略，在已知网络结构上优化得1852913USD/a，优化时间为23832s，由于依赖已知结构，普适性略显不足。文献[6]采用SA-RFO 混合算法优化所得，结果为1900614USD/a，优化时间为24492s。文献[31]则通过动态节点策略减少模型计算量，获得优化结果1910630USD/a。通过与文献结构对比发现，除本文和文献[32]外，均存在C4流股公用工程未消去或C5 上公用工程过大的情况。而本文结构则是形成巧妙的耦合关系消去C4 的公用工程和减少了C5 公用工程能耗，且最小传热温差只出现在H6 和H22 流股上的换热器，为15.0℃，符合实际情况。其他文献由于全局搜索能力不足或局部搜索精度不足，导致结构耦合程度差，或热量分配不合理未能消去或减少C4、C5 上公用工程。相比文献[31]，虽然设备投资费用增加了13163USD/a，但是公用工程能源消耗费用下降了37180USD/a，总费用减少了24017USD/a。

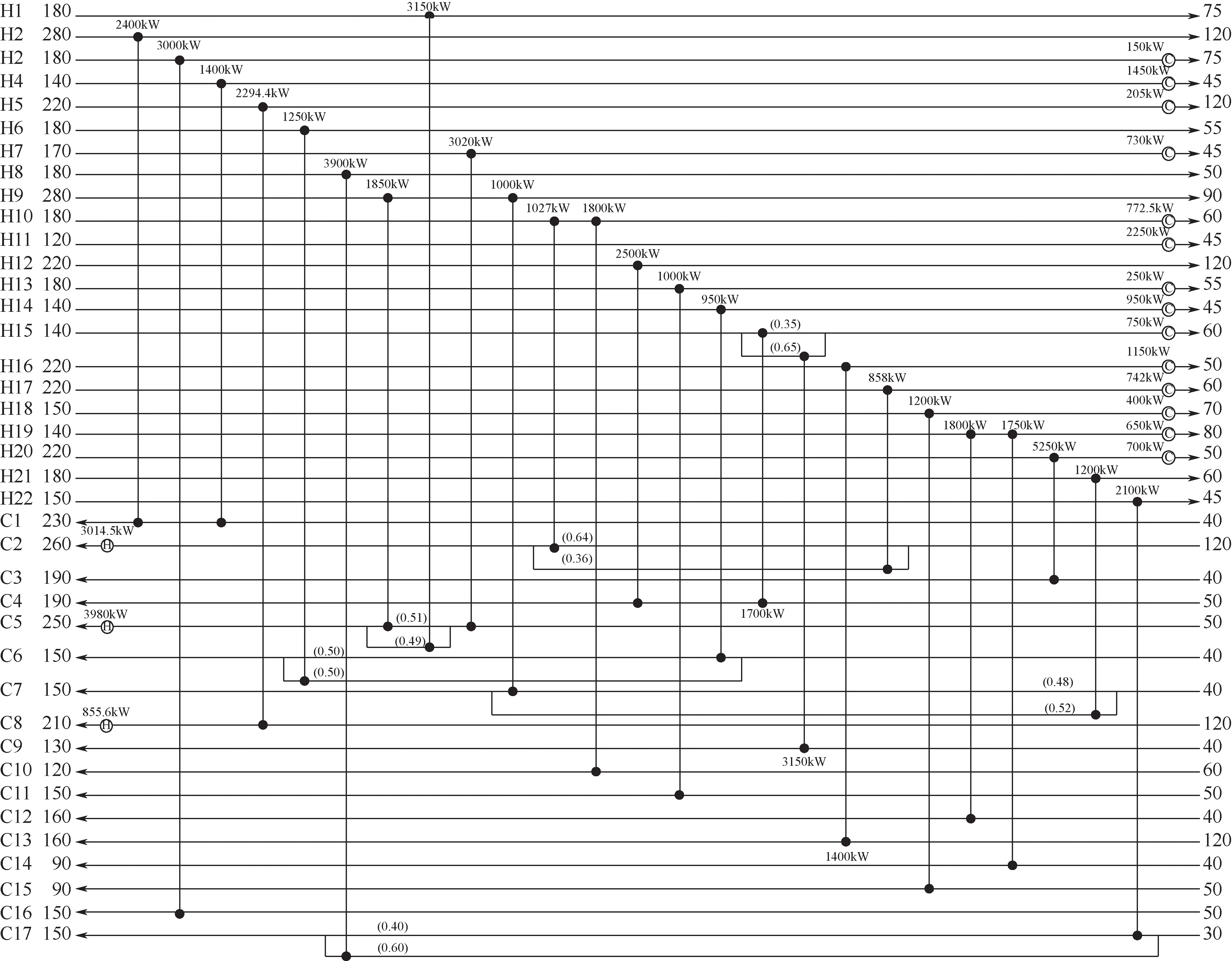
图11 算例2对应网络结构

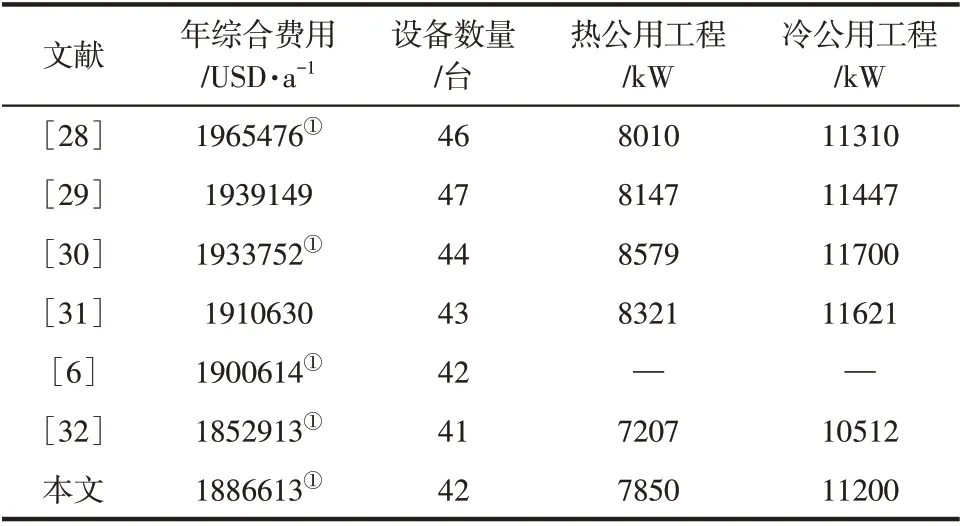
表2 算例2优化结果与文献结果对比

并行双层RWCE 算法加速比理论上限为32（计算机核心为32），实际试验中最高加速比是27.2，为启用45超线程运算时获得。算例1加速比是26.0，算例2 加速比是26.6，均为61 超线程运算，说明相同线程时问题规模越大，加速比也越大。但由于十分接近计算机性能极限，因此问题规模对加速比的增幅有限。线程数和问题求解规模均能影响加速比，原因在于问题规模越大，产生不同类型的运算指令越丰富越及时，在超线程处理下，可大幅减少CPU 不同计算部分的闲置时间，从而提高加速比。因此，在合理的并行线程数下，问题规模越大，加速比越大。

5 结论

针对基础RWCE 算法求解大规模换热网络时局部搜索精度不足的问题，本文提出了基于OpenMP 并行计算的并行双层RWCE 算法。该算法结合了并行技术和原算法特点，通过线程分配构建基础层和精细层，在优化全程兼顾全局与局部搜索能力。此外，本文检验了并行双层算法优化质量与效率，相比于基础算法，消除了差解代替优解的不良现象，大幅提升了大型网络的优化效率。最后优化20SP和39SP算例进行验证，计算结果表明，算法全局搜索能力和局部搜索能力都得到强化，同时发现加速比随线程数和问题规模增大而增大。这些特征对于大型换热网络优化问题的高效准确求解具有重要指导意义。

然而，本文未与并行计算特点结合，研究相关优化策略。作者将在此基础上，充分发挥并行计算与RWCE 算法特性，进一步开发出提高换热网络质量的策略。

，，——换热器、冷、热公用工程的换热面积，m

——换热面积费用系数

，——冷、热公用工程的运行费用系数

——设备固定投资费用，USD/a

FCP——流股的热容流率，kW/℃

Δ——最大游走步长，KW

LMTD——对数平均温差，℃

——流股总节点数

，——冷、热流体股数

，——冷、热流股的主节点数

，——冷、热流股分流数