边界压力波动对液膜端面机械密封空化及性能的影响

2022-10-30张金亚张家祥沈宗沼陈逸

化工进展 2022年10期

张金亚，张家祥，沈宗沼，陈逸

（1 中国石油大学（北京）机械与储运工程学院，北京 102249；2 中国石油大学（北京）过程流体过滤与分离技术北京市重点实验室，北京 102249；3 合肥通用机械研究院有限公司，安徽合肥 230031）

机械密封因其良好的密封特性被应用于泵、风机和压缩机等旋转机械中，随着工业技术的发展，泵用机械密封逐步应用于混相介质、压力波动及高温等严苛环境中。离心泵在运行过程中产生的压力波动原因有泵内旋转叶片和静止部件互相干扰所产生的压力波动以及气液两相流动条件下产生的压力波动，前者产生的压力波动幅值较小，后者则相对较大。压力波动的产生将改变密封端面的受力及密封端面的空化分布，使得密封环发生振动，易造成机械密封损坏，因此对机械密封在压力波动工况下进行研究有着重要意义。

目前，离心泵内压力波动的研究较为广泛，池忠煌对低比转速离心泵进行了研究，其压力波动的实验测量结果近似呈现三角函数波动。王松林等研究了离心泵瞬态空化流动及压力脉动特性，叶轮内压力脉动最大幅值由进口至出口逐渐增大，且空化流动时压力脉动最大幅值大于非空化工况。陈轲等对侧流道泵内压力脉动特性进行了研究，侧流道泵内部流动复杂、湍流强度极大，会产生较强的压力脉动。刘厚林等对双流道泵内压力脉动进行了CFD 计算及测试，表明叶轮流道内不同位置处点的压力波动在一个周期内呈现周期性变化规律。而压力波动工况下泵用机械密封的研究鲜有报道，近年来的研究主要集中在空化试验、空化机理及空化算法。彭旭东等综述了近五十年来汽液两相端面机械密封的研究现状，归纳出了机械密封的典型热源及其热传播途径，阐述了机械密封的相变原理，总结了端面流体膜参数的测量技术与方法。孟祥铠等基于液体润滑理论和小扰动法，建立了考虑液膜空化的密封微扰膜压控制方程，采用有限单元法对端面液膜三自由度微扰下的液膜刚度和阻尼系数进行了数值求解，分析了不同参数对液膜密封动力系数的影响，并对空化条件下凹陷表面的黏度楔效应进行了研究，旨在深入研究机械密封的压力分布和承载力的作用。马学忠等基于遵循质量守恒的JFO 空化边界条件，采用SUPG 有限元方法求解Reynolds 方程，研究了反向螺旋槽的空化效应，并提出了一种新型的正反向螺旋槽组合端面密封结构。

Tokunaga等进行光滑平环和微造型环的空穴可视化对比实验，实验过程中发现密封环表面产生大量的微小空穴区，且空穴区的位置和液体流动路径随着时间的变化一直在波动。在机械密封端面空化机理方面，Zeus指出局部的流速改变导致局部压力降低是空化发生的必要条件。Etison 等认为空化是形成端面开启的重要原因。此外，由于液膜端面产生空泡，能够有效阻止端面的泄漏和减少端面摩擦，实现空化减阻。Findlay通过研究短轴承近似法对带波纹度的密封端面液膜压力分布问题，提出了空化是形成液膜承载力的重要原因。Li等、Hao 等对螺旋槽密封端面液膜空化机理和流体动压润滑性能进行了探索，指出膜厚较小时在槽内膜厚发散处，液膜开始破裂形成空化区，同时进行了可视化试验。徐鲁帅等利用Matlab 建立密封环端面间隙液膜三维模型，采用有限差分法离散基于JFO空化边界条件的雷诺方程，分析了工况连续变化及压力扰动对密封瞬态特性的影响，相比于转速瞬时变化，压力瞬时变化过程中挤压效应对密封性能的影响更为显著。在机械密封端面空化算法方面，Xue 等等研究发现JFO 空化边界条件预测螺旋槽机械密封的分离速度比Reynolds空化边界大，而且更接近实验结果。

本文针对压力波动出现在液膜密封的内外径侧进行研究，并设定内、外径侧压力遵循三角函数变化，采用CFD 方法，基于Mixture 多相流模型中的Zwart-Gerber-Belamri 空化模型进行数值计算，探究压力波动条件下液膜密封端面空化演变及其密封性能变化，并进一步分析不同波动幅值及波动周期对液膜密封的影响，为机械密封在压力波动工况下运行提供理论基础。

1 物理模型及网格划分

1.1 物理模型

泵出型机械密封在动环端面开槽的几何模型如图1所示，分为槽区、堰区和坝区，槽型线采用对数螺旋线，如式(1)所示。

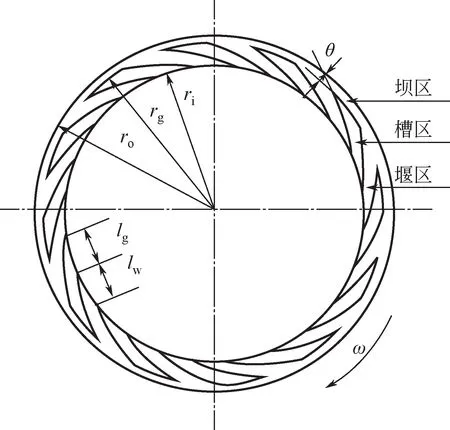
图1 螺旋槽机械密封示意图

式中，为密封环内径，mm；为螺旋线展开角，(°)；为螺旋角，(°)。

为了提高对数螺旋线的精度，采用MATLAB计算螺旋线的点坐标。根据文献[29]的密封尺寸可知，密封环内径为44.25mm，外径为53.25mm，螺旋角为18°，槽径比为0.7，槽宽比为1，槽数为12，膜厚为3μm，槽深为8μm，运行工况中的转速为5000r/min，空化压力为3.54kPa，考虑到温差对机械密封有较大影响，需安装冷却装置来保证机械密封端面的温度稳定。机械密封按照补偿环是否随轴转动分为旋转式机械密封与静止式机械密封，机械密封的安装形式如图2所示，红框内流体为研究对象，即机械密封液膜，图2(a)中泵内介质与机械密封的外径侧相接触，即发生压力波动的位置出现在机械密封的外径侧；同理，图2(b)中泵内的压力波动作用在机械密封的内径侧。

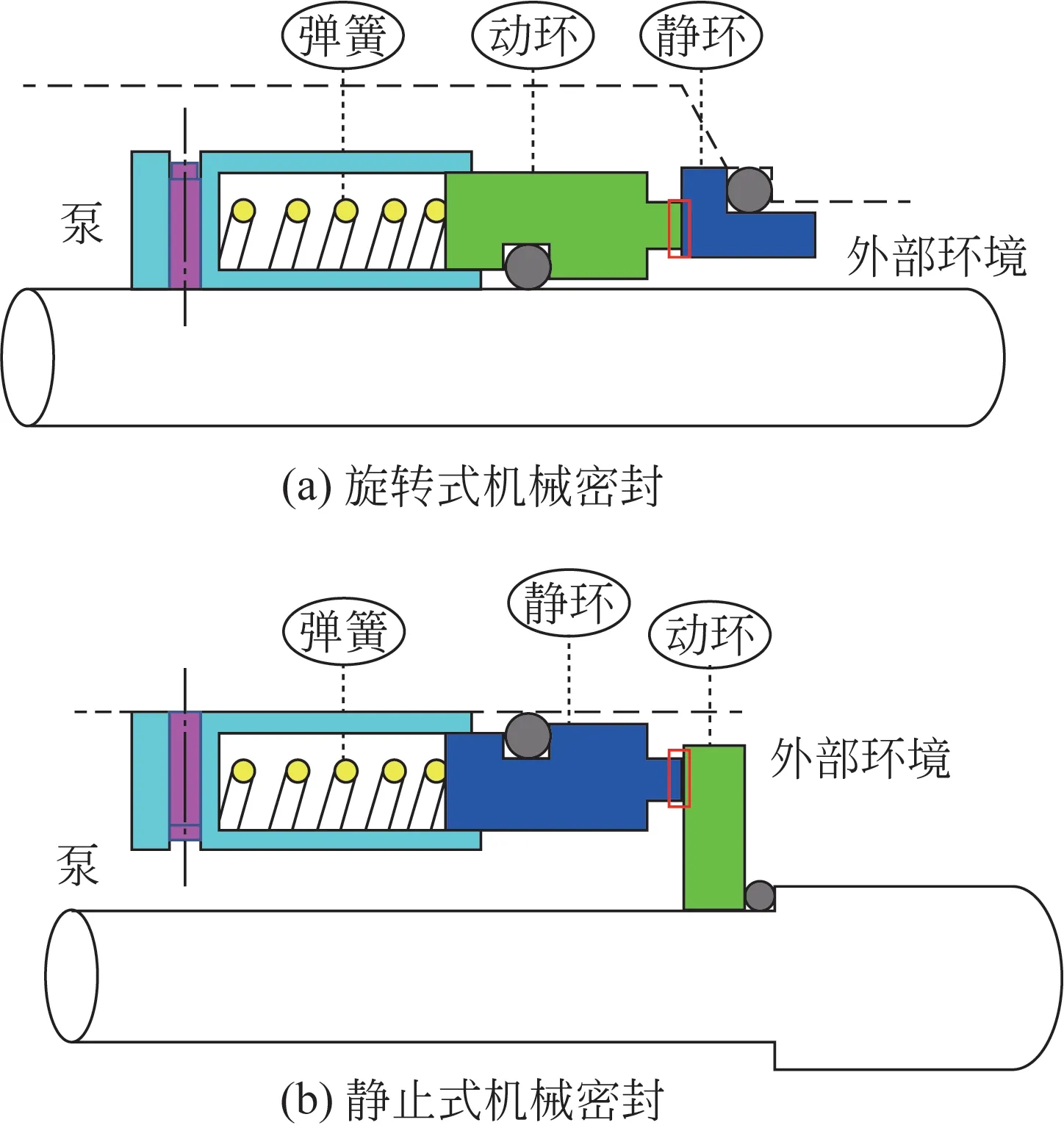
图2 机械密封示意图

1.2 网格划分及验证

为了提高计算效率，选取1/个周期进行网格划分。采用Gambit进行网格划分，如图3所示，视图中将液膜厚度方向上放大了1000 倍。由于空化在密封端面受局部压力影响，故而受端面网格尺寸影响较大。设定网格层数不变，即膜厚方向上网格为6层，槽深方向网格为16层。通过改变端面网格尺寸来进行空化条件下的网格无关性验证，此时外径侧压力设定为大气压力，如图4所示。随着网格数的增加，气相体积分数逐渐减小，网格数约为37 万时基本稳定，因此选择约37 万网格开展下一步数值计算。

图3 单螺旋槽网格划分策略

图4 网格无关性验证

为了验证空化模型的正确性，建立斜线槽模型，密封压力0.03MPa，并与文献[30]所观察到的空化现象作对比，如图5所示。从图中可以看出模拟中的空化位置与文献现象较为接近，且空化区域的外形也基本一致，模拟与文献中实验出现偏差的原因在于模拟中忽略了重力以及端面粗糙度的影响。此外，对机械密封端面的压力分布进行验证，如图6 所示，进一步说明本文数值模拟的正确性。空化分布及压力分布的验证说明模拟结果与文献结果吻合较好，可以开展后续研究。

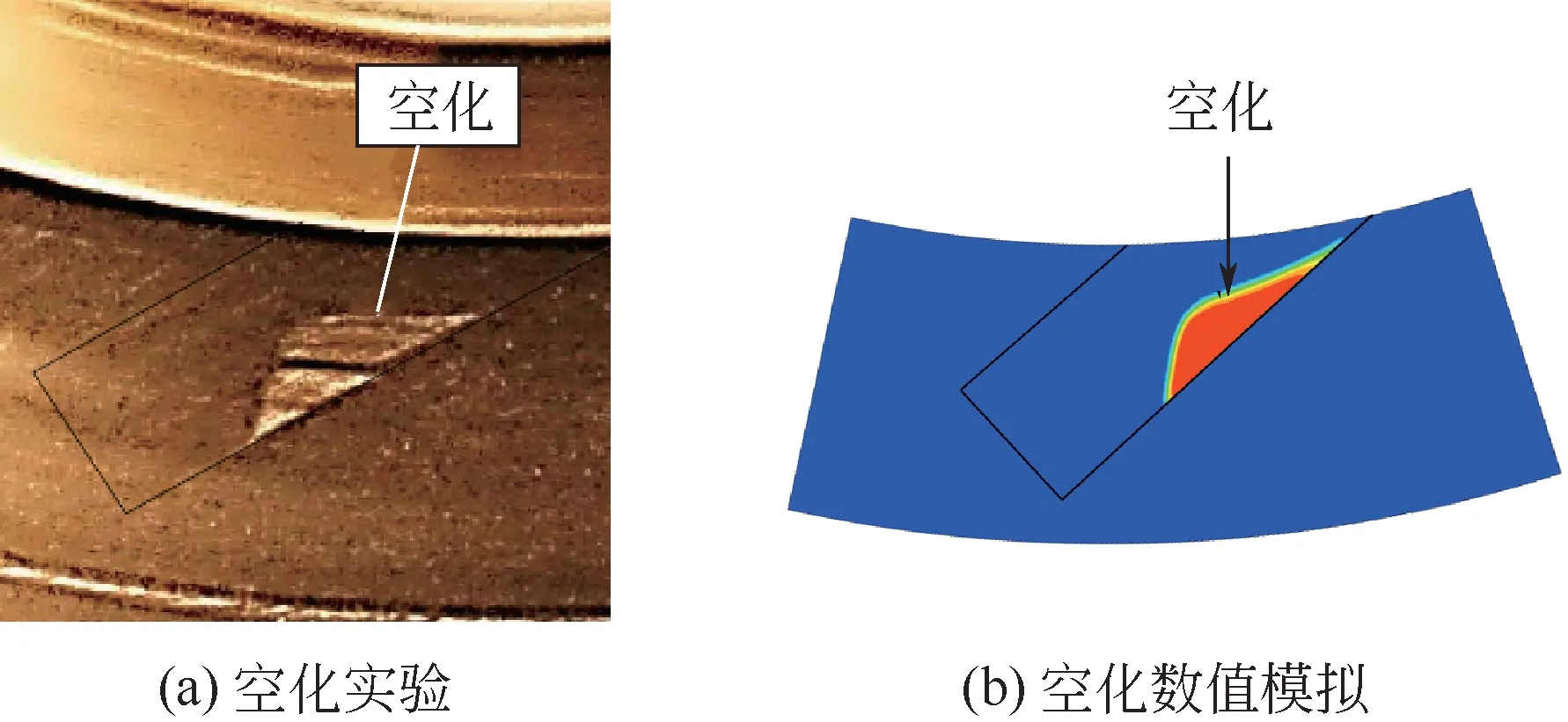
图5 密封端面空化分布验证

图6 密封端面压力分布验证

2 数值计算模型及边界条件设定

2.1 计算模型

为了降低压力波动条件下机械密封混相润滑膜的复杂性，忽略对计算影响较小的因素，并作如下假设：

①润滑膜间隙为层流且不可压缩；

②忽略密封环端面粗糙度的影响；

③不考虑摩擦热对介质的影响，认为是等温状态，温度为300K；

④边界处介质流体与密封端面无滑移，忽略密封环微变形对流场的影响。

ANSYS FLUENT中提供了三种多相流模型，分别为VOF（Volume of Fluid）模型、混合（Mixture）模型和欧拉（Eulerian）模型。密封间隙的空化是由螺旋槽底部的局部低压产生的，故选Mixture 模型更为合适。空化模型选择Mixture 多相流模型中与实验值更为接近且稳定性较好的Zwart-Gerber-Belamri模型。

基于空化的连续性方程、动量方程及气相传输方程如式(2)～式(4)所示。

液膜内气相体积分数为液膜内的空化产生的气相体积与液膜总体积之比[式(7)]。

式(2)～式(7)中，为混合物密度；为质量平均速度；为混合黏性系数；、分别为气泡产生、溃灭源项；下角标v为气相，l为液相；为气相体积分数；为密封膜体积；为密封膜空化的气体体积；为密封膜液体体积。

2.2 边界条件

受现场运行过程中流量调节、流体激振等因素影响，泵内压力出现大幅度的波动且呈现出一定的规律，经密封通道传递至密封腔内，进而作用在机械密封的边界处。本文中设定压力波动遵循三角函数变化，遵循式(9)、式(10)。

为了探究压力波动对机械密封的影响，波动时间为3，即经历三次压力波动峰值。压力波动停止时，考虑到压力波动对端面空化及密封性能具有迟滞效应，计算结束时间设定为6。由文献[6]中实验可知，低比转速离心泵流量为70m/h时，压力波动范围为1.8～3.2MPa，泵内的压力波动较大，此外，泵内遭遇极端工况（进口含气、流量调节、流体激振等因素）时，将会使泵内压力波动继续抬高，考虑到密封通道的压降作用，本文将机械密封边界处的压力幅值设定为0.8MPa。模拟计算中离散格式则采用SIMPLEC算法，其有助于计算收敛，梯度空间离散采用Green-Gauss Cell Based，压力项采用PRESTO!格式，体积分数项采用一阶迎风格式，其余采用二阶迎风格式。嵌入压力波动前需保证端面稳定的空化区域，计算流程如图7所示。

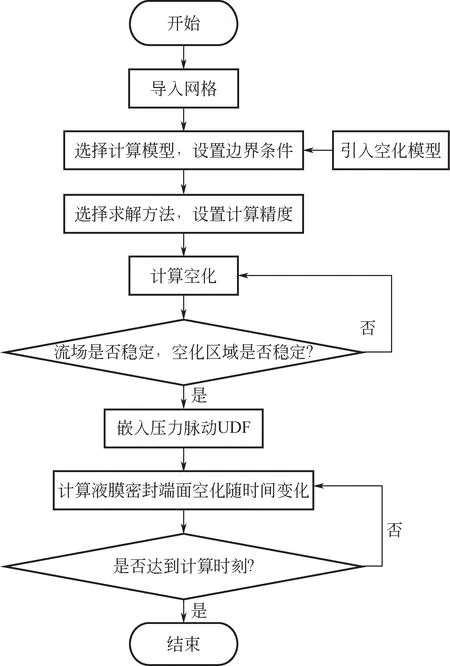
图7 计算流程

3 结果及讨论

液膜密封在压力波动工况下，膜内的气相体积分数随时间变化，密封性能参数（开启力、泄漏量）也随时间变化。探究内、外径侧压力波动条件下对密封端面空化及密封性能的影响，并进一步分析压力波动幅值与波动周期产生的影响。

3.1 压力波动下的端面空化演变过程

3.1.1 外径侧压力波动

内径侧压力为0.1MPa、波动周期为0.5s、波动幅值为0.2MPa 时，外径侧压力波动对端面空化及密封性能的影响如图8所示，可以看出，气相体积分数与密封性能参数均与压力波动规律一致，气相体积分数与外径侧压力波动之间存在相位差，迟滞时间约为0.1s，而密封性能参数与外径侧压力波动之间有着较好的跟随性。内径侧压力波动幅值为0.2MPa，气相体积分数的波动幅值约为0.05%，波动峰值略小于初始时刻的气相体积分数，泄漏量的波动幅值约为3mg/s，开启力的波动幅值约为16N，此波动工况下，三者的波动幅值均不大。

0～0.3s 端面空化变化如图9 所示，空化聚集在螺旋槽内的背风一侧，此区域的压力低于饱和蒸气压，说明液膜密封中的空化主要是压降导致的，气体受到周向力及离心力的共同作用而聚集，图9中的4个时刻处在图8中气相体积分数曲线中初始时刻至第一个波谷时刻之间，端面空化区域的变化较小。此外，密封润滑膜膜厚为3μm，压力在膜厚方向上变化较小，空化产生的气体主要聚集在槽区，端面空化区域尺寸要比膜厚大得多，因此可用气相体积分数的变化来评价端面空化的变化情况。

图9 外径侧压力波动密封端面空化演变

3.1.2 内径侧压力波动

外径侧压力为环境压力，内径侧压力波动对端面空化及密封性能的影响如图10所示，并与图8对比，内径侧压力波动时，气相体积分数与密封性能参数也与压力波动规律一致，但内径侧压力波动与气相体积分数、密封性能曲线均产生了迟滞现象，气相体积分数与泄漏量的同步性较好，与外径侧压力波动的迟滞时间约为0.25s，开启力的迟滞时间约为0.1s。气相体积分数与泄漏量的同步性较好的内在原因在于液膜内的压力变化，液膜内的压力变化直接影响低压区域的大小，进而影响空化气体的生成，液膜内的压力也会影响泄漏量的变化。其外在表现为空化生成的气体会占据一部分液膜体积，即空化气体体积增大时泄漏量也增大。外径侧压力波动幅值为0.2MPa，气相体积分数波动幅值约为2%，其峰值小于初始时刻的峰值且变化幅度较大，波动幅值为外径侧压力波动条件下的40 倍。泄漏量的波动幅值为6mg/s，波动幅值为外径侧压力波动条件下的2倍。开启力的波动幅值为50N，波动幅值为外径侧压力波动条件下的3倍。

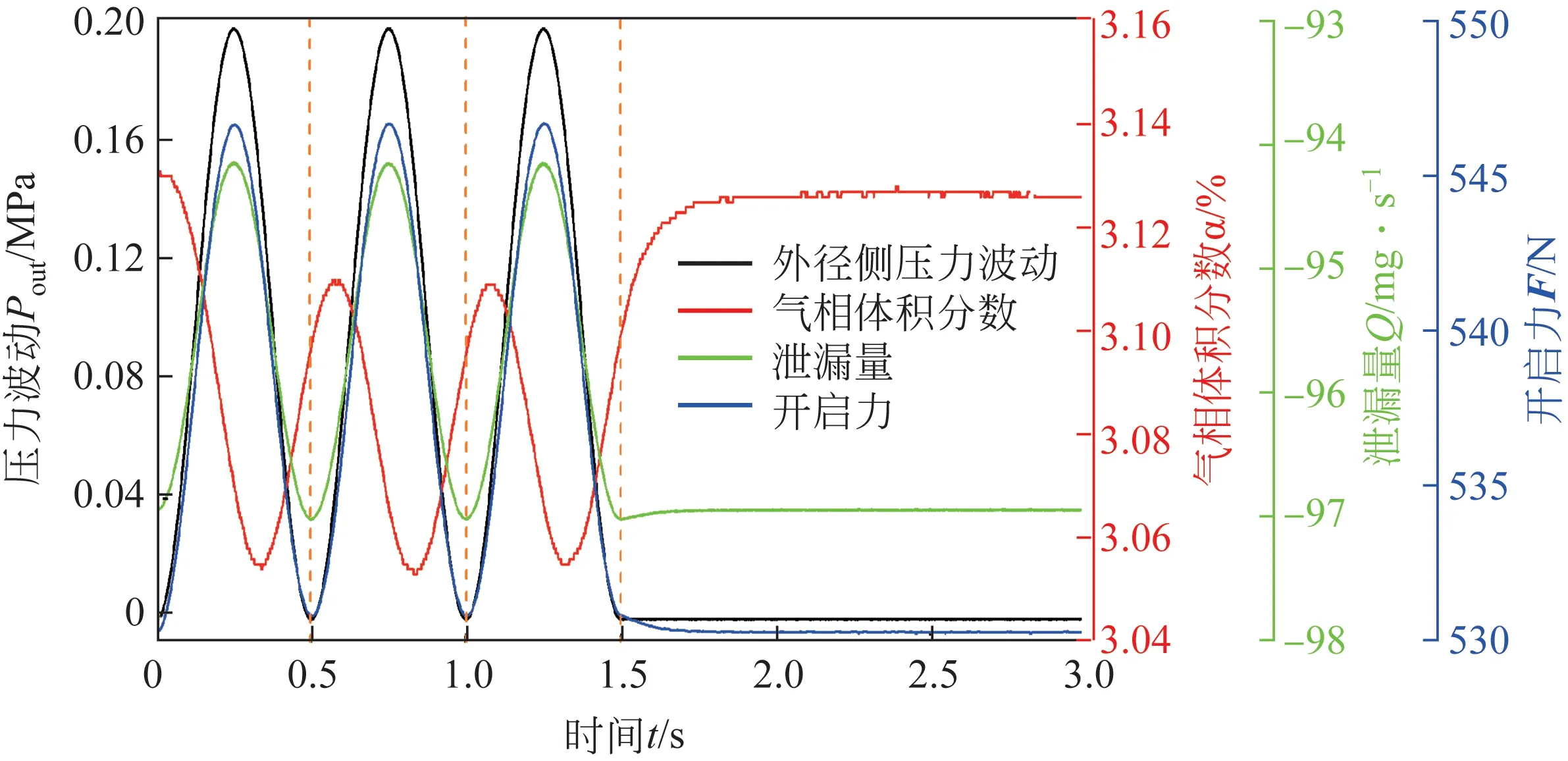
图8 外径侧压力波动对空化及密封性能的影响

图10 内径侧压力波动对空化及密封性能的影响

0～0.3s 端面空化变化如图11 所示，时刻取值与图9一致，气相体积分数曲线中初始时刻至第一个波谷时刻逐渐降低时，端面空化区域也在逐渐变小，但其外形近似一致，气相体积分数变化幅值较大，空化区域也随之明显变化。端面压力分布如图12 所示，低于设定的饱和蒸气压时将产生空化气体，由密封端面的压力分布可知空化气体主要聚集在槽内的低压区域。随着内径侧压力的升高，低压区所占面积逐渐减小，端面的空化区域也在逐渐减小。波动周期为0.5s，波动幅值为0.2MPa 下内径侧压力波动与外径侧压力波动相比，内径侧压力波动对端面空化的影响更大。

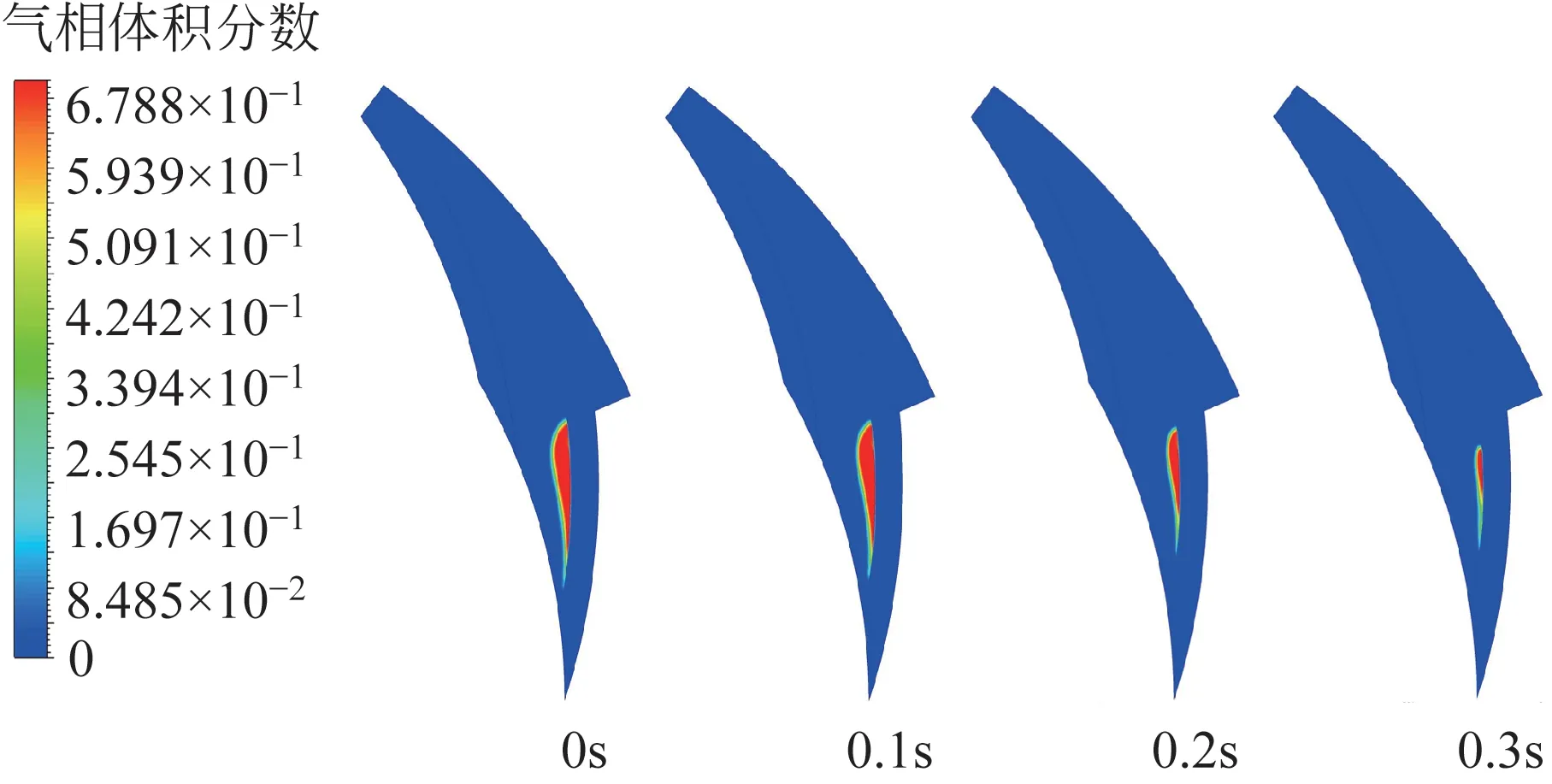
图11 内径侧压力波动密封端面空化演变

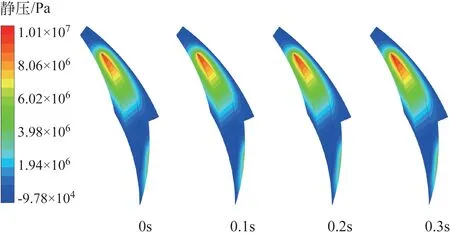
图12 内径侧压力波动密封端面压力分布

3.2 外径侧压力波动对端面空化及密封性能的影响

为了探究外径侧压力的波动幅值与波动周期对端面空化及密封性能的影响，对不同波动幅值及波动周期进行数值计算。监测的外径侧压力波动如图13所示，外径侧压力波动由UDF功能定义。

图13 外径侧压力波动

气相体积分数随时间变化如图14 所示，随着波动幅值的增大，气相体积分数逐渐降低；随着波动周期的增大，气相体积分数的波动逐渐接近压力波动变化规律，且波动的最小值表现为先减小后基本稳定，但整体的变化幅度不大。定义波动结束时恢复稳定所需时间与波动周期的比值为波动恢复系数，随着波动周期的增大，逐渐减小。

图14 气相体积分数随时间变化

波动周期为0.1s时，在压力波动曲线处于波谷时，气相体积分数并非处于波峰，表现为迟滞现象。此外，其峰值表现为逐级降低，气相体积分数的最小值为2.95%，相较于初始时刻减小了约0.175%。波动幅值越大，气相体积分数的波动程度也越大，并不遵循三角函数变化。至0.6s时，气相体积分数逐渐趋于平稳，说明设定计算周期为0.6s 的合理性。波动周期为0.25s 时，气相体积分数依然与外径侧压力波动保持着一定的相位差，但迟滞时间有所减小。气相体积分数的波动趋近于三角函数变化，其波动峰值相比于图14(a)有所减小，最小值接近2.9%，波动时间约为1.1s 时，气相体积分数基本保持不变。波动周期为0.5s时，气相体积分数的波动遵循三角函数变化，与压力波动的相位差与图14(a)、(b)相比有所减小，波动最小压力的峰值接近2.85%，气相体积分数的最小与最大波动幅值约为0.01%与0.23%，随着压力波动峰值的增大，气相体积分数最小值逐渐减小且变化较大，其最大值则处于3.07%～3.12%之间。至1.8s时，气相体积分数基本稳定。波动周期为0.75s 与1s 时，其变化特征基本与图14(c)一致，不同之处在于图14(d)、(e)中的最小值均为2.83%左右，说明在0.5～1s 时间内存在着临界周期，使得气相体积分数的最小值基本稳定。

机械密封的主要评价指标为开启力与泄漏量，外径侧压力发生波动下的密封性能随时间变化如图15、图16所示。可以看出，开启力与压力波动的跟随性很强，即外径侧压力处于波谷时，开启力也处于波谷，而泄漏量与压力波动之间存在较小的相位差。随着波动幅值的增大，开启力与泄漏量波动幅值均有所增大，压力波动增大一倍时，开启力与泄漏量的波动幅值也增大一倍。此外，外径侧压力的增大有助于提高机械密封性能，即增大了开启力，降低了泄漏量。当波动周期在0.5s以上时，如图16(c)～(e)所示，泄漏量波动与压力波动跟随性良好。压力波动幅值为0.8MPa，而开启力波动的最大波动幅值约为63N，泄漏量波动的幅值为11mg/s，密封性能参数的波动较小。当外径侧压力发生波动时，液膜密封的气相体积分数与密封性能参数变化较小，当机械密封的结构阻尼与弹簧弹力能够克服开启力带来的变化时，液膜密封的补偿环则不会发生振动，由于外径侧压力与密封性能的跟随性良好，可用外径侧压力来预测密封性能的变化。

图15 开启力随时间变化

图16 泄漏量随时间变化

3.3 内径侧压力波动对端面空化及密封性能的影响

为了探究内径侧压力的波动幅值与波动时间对端面空化及密封性能的影响，设定外径侧压力为环境压力，对不同波动幅值及波动周期进行数值计算。监测的内径侧压力波动如图17 所示，其压力波动由UDF功能定义。

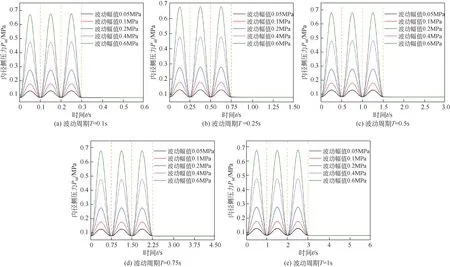
图17 内径侧压力波动

压力波动时，气相体积分数随时间的变化如图18 所示，可以看出波动曲线中存在气相体积分数为0，即端面空化消失现象，并且随着波动周期的增加，空化消失时间先增大后基本不变，说明内径侧压力在0.28～0.68MPa 之间存在临界压力使得端面空化消失。随着波动幅值的增加，气相体积分数的逐渐降低且幅值较大，与图14 对比，说明内径侧压力波动对气相体积分数的影响更大。波动周期增大，气相体积分数与压力波动的相位差逐渐减小，气相体积分数的最小值呈现先减小后基本不变的趋势，波动恢复系数逐渐减小。

波动周期为0.1s时，气相体积分数波动变现为逐级递减，波动幅值为0.6MPa 时出现端面空化消失，即气相体积分数为0，但其维持的时间较短，说明临界压力与波动周期有关。气相体积分数波动并不遵循压力波动的变化规律，与图14(a)一致，但其变化的幅值较大。至0.6s时，液膜密封内气相体积分数波动基本稳定。波动周期为0.25s 时，如图18(b)所示，气相体积分数波动遵循近压力波动变化规律，波动幅值为0.4MPa 与0.6MPa 时，在波动上升期间基本重合，此波动幅值下均存在临界压力，且波动幅值为0.6MPa时的端面空化时间更长，波动时间约1.1s，端面空化基本稳定。波动周期0.5s 及以上时，如图18(c)～(e)所示，气相体积分数波动遵循三角函数变化，与压力波动存在相位差。波动幅值为0.4MPa 与0.6MPa 时，端面气相体积分数为0 的时间较长。波动周期为0.75s 与1s 时，气相体积分数的波动峰值基本一致，说明在0.5～0.75s 之间存在临界周期，使得气相体积分数波动峰值保持不变。

内径侧压力波动时，端面开启力与泄漏量的变化如图19、图20 所示，端面空化消失时，使得开启力与泄漏量出现突增现象，随着压力波动幅值的增大，开启力与泄漏量均增大，说明空化的产生有利于减小泄漏量。对比图18～图20可以看出，密封端面的空化对压力波动具有抑制作用。即端面空化消失时，密封性能曲线出现急剧变化；液膜内发生空化时，其密封性能曲线变化近似呈现三角函数变化（与给定的边界压力波动函数形式一致）。波动周期为0.1s 与0.25s 时，密封性能参数波动并不遵循三角函数变化，而波动周期大于0.25s 时，波动幅值为0.05MPa、0.1MPa 及0.2MPa 时，其波动变化遵循三角函数变化。与此同时，密封性能波动与压力波动存在相位差，且随着波动时间的增大，波动恢复系数逐渐减小。

图18 气相体积分数随时间变化

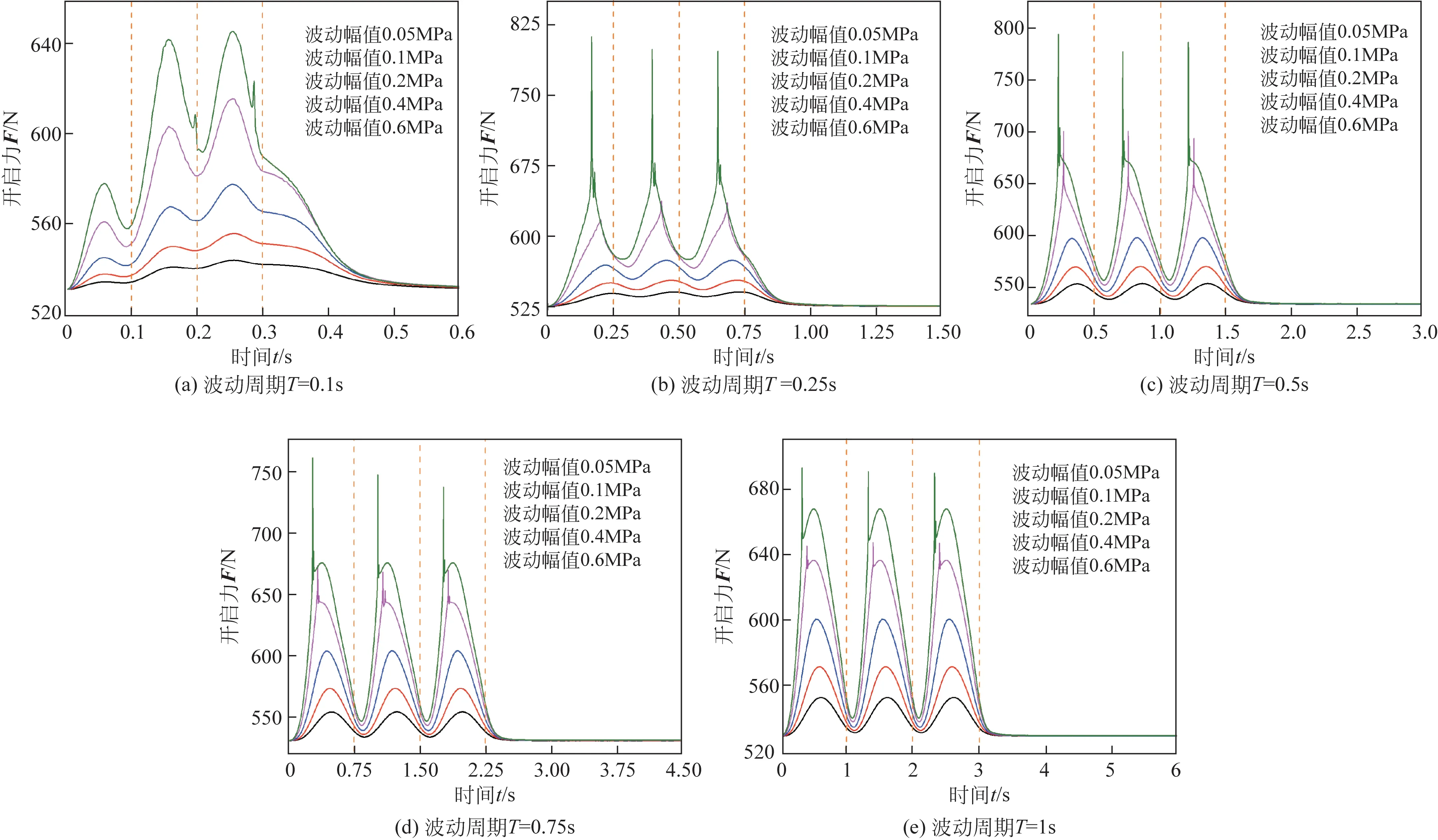
图19 开启力随时间变化

图20 泄漏量随时间变化

波动周期为0.1s 时，端面空化消失时间较短，在波动时间0.2s及0.3s附近存在小幅度的突增，开启力的波动峰值逐渐增大，其波动最大值约为110N，与图15(a)差别较大，泄漏量的波动最大值约为12mg/s，与图16(a)的差别较小。而波动周期为0.25s 时，端面空化消失，导致开启力与泄漏量变化曲线急剧变化，开启力峰值接近825N，泄漏量的峰值接近-118mg/s，此时将使得补偿环发生振动，导致密封环失稳。波动周期逐渐增大时，开启力与泄漏量的峰值均逐渐减小。内径侧压力波动对液膜密封端面空化的改变较为明显，当端面空化消失时，对密封性能参数的改变较大，开启力将克服机械密封结构阻尼与弹簧弹力，继而致使补偿环发生振动，从而改变液膜密封性能。