大跨度变截面连续箱梁桥气动特性CFD研究

刘想，王若宇，何源涛

(中国水利水电第五工程局有限公司，成都，610066)

0 引言

大跨度变截面连续箱梁桥[1-3]由于其跨越能力强，造价低及结构刚度大等诸多优点被广泛应用于公路及铁路桥梁的建设中。然而，随着桥梁跨度和桥墩高度的不断增大，在悬臂施工过程中，最大悬臂施工状态下桥梁的静风稳定性是一个不可忽视的问题。

马玉娟[4]针对某超高墩连续刚构桥开展静风稳定性分析，发现最大双悬臂阶段桥梁结构不会发生扭转发散；李永乐等[5]采用CFD分析方法讨论了某大跨斜拉桥主梁截面的气动特性，并对主梁截面开展了优化分析；赵天野等[6]研究了侧风作用下桥上车辆的气动力特性，考虑了车辆位置及风速等因素的影响。可以看到，以往大部分学者通常采用单一的主梁跨中截面气动力系数开展静风稳定性计算，但是大跨度变截面桥梁在跨中截面和悬臂根部截面处的主梁高度往往相差较大，可能进一步会导致其气动特性有较大的变化。因此，需要研究不同高宽比对主梁截面气动系数变化的影响。

本文依托某大跨度变截面预应力连续箱梁桥为背景，基于流体动力学分析软件FLUENT[7]开展不同高宽比下主梁气动力系数数值仿真分析，建立了不同位置处主梁截面的CFD计算分析模型，并进一步研究了主梁周围气动力特性随主梁高宽比的变化，讨论风攻角对主梁气动力系数的影响，可以为大风环境下大跨度变截面连续箱梁桥的静风稳定性分析和施工安全提供必要的理论依据。

1 数值分析方法

1.1 CFD分析模型

本文用大型流体力学计算软件FLUENT对大跨度变截面宽幅箱梁桥的典型断面进行数值风洞仿真模拟，从而获得不同高宽比断面结构的流场形式并计算得出桥梁的气动力系数。其中，桥梁计算模型无缩尺，桥梁结构断面简化计算模型如图1所示。为满足阻塞比要求，计算区域高度大于20H，长度大于30D，其中H为主梁高度，D为主梁宽度。应用CFD网格技术，将迎风左侧边界设置为速度入口边界，来流设置为均匀流，来流速度为15m/s，其中湍流强度按照一般风洞试验对均匀流场的要求设置为0.5%；背风右侧边界设置为压力出口边界；上下边界采用对称边界条件。桥梁表面定义为光滑壁面。

由图2可以看出，本模型采用非结构化四边形网格形式划分网格，网格最小尺寸为0.002m，网格总数达到90万左右。将计算区域分为内部和外部网格区域，靠近桥梁结构附近范围内的网格较密，外部区域的网格逐步放大，这种网格划分方式既保证了结果精度又兼顾了计算成本。湍流模型选用SSTk-ω，采用SIMPLE算法解决压力和速度分量耦合的问题。为提高求解精确性，动量方程、湍动能方程以及湍流耗散率方程都选择二阶离散格式。采用非定常模型进行模拟，计算步长取0.0005s。

图1 CFD分析模型计算区域示意

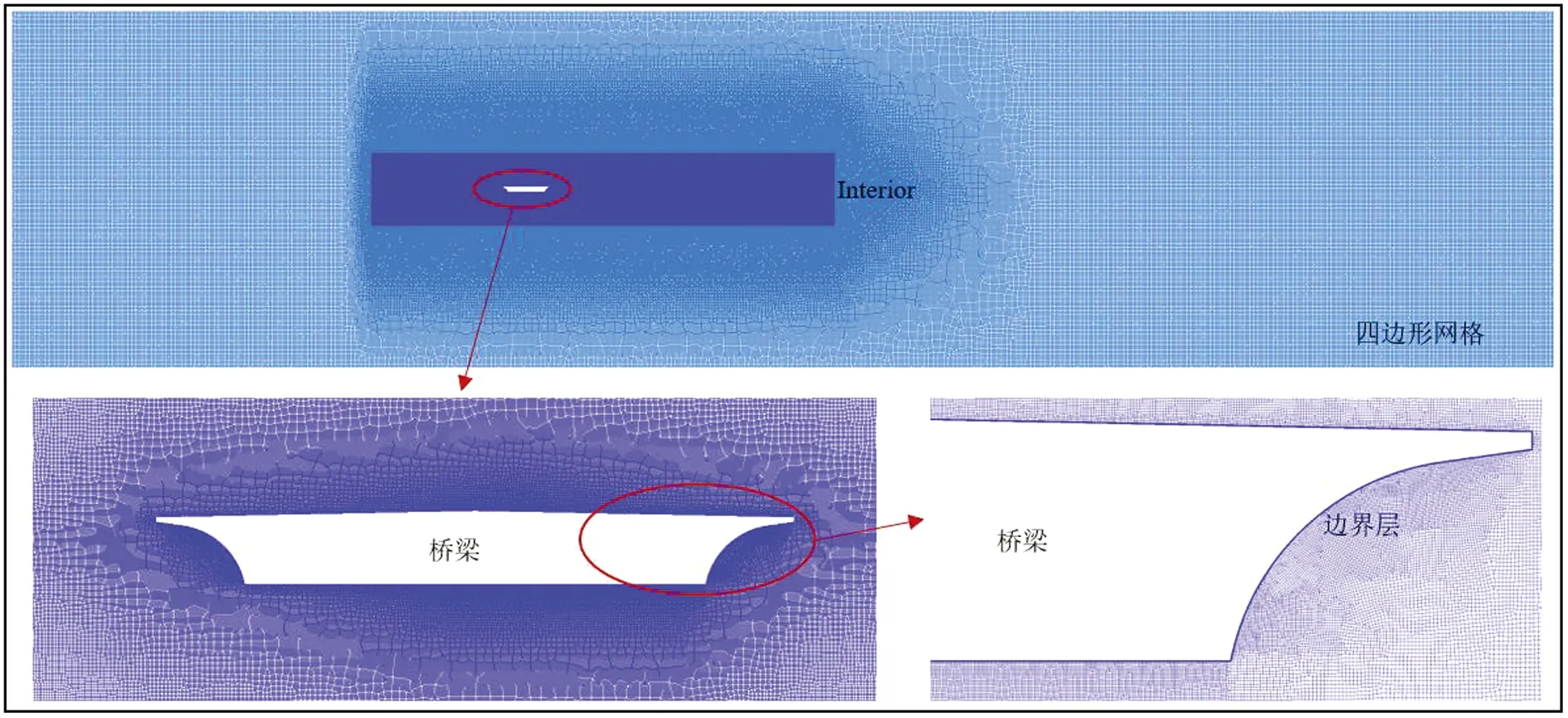
图2 CFD分析模型整体和局部网格划分

1.2 三分力系数计算

主梁三分力系数是表征桥梁结构断面在来流风作用下单位面积受力大小的无量纲系数。作用于主梁断面上的三分力系数通常按照坐标系的不同分为体轴坐标系和风轴坐标系，如图3所示。

图3 三分力系数坐标系

其中，风轴坐标系下的阻力系数、升力系数和力矩系数可以分别根据下式定义：

阻力系数：CD(a)=FD(a)/(0.5ρU2HL)；

升力系数：CL(a)=FL(a)/(0.5ρU2DL)；

力矩系数：CM(a)=MZ(a)/(0.5ρU2D2L)。

式中，a为来流风攻角；U为来流平均风速，m/s；ρ为空气密度，取1.225kg/m3；H，D，L分别为主梁截面的高度、宽度和长度，m；FD、FL、MZ分别为主梁所受的阻力、升力和力矩。

采用流体力学分析软件FLUENT对某大跨度预应力宽幅变截面箱梁桥(59m+100m+59m)开展流场分析及气动力系数研究，主梁桥面宽度为26m，本文选取高度分别为300cm(跨中截面)、395cm、495cm和590cm(根部截面)的桥梁截面开展研究，对应的高宽比分别为1∶83、1∶66、1∶53和1∶44。计算得到0°攻角下风速为15m/s时主梁截面的三分力气动系数分别如表1所示。

表1 风轴坐标系下主梁截面气动力系数

由表1可以看出，随着主梁截面的高度不断增大(高宽比逐渐增大)，主梁的阻力系数由1.278逐步增大到1.811，升力系数也随之增大，其大小由-0.101增大到0.519。相反地，主梁截面的力矩系数随高度增大而减小，其大小由-0.132减小到-0.254，但主梁截面力矩系数的绝对值随着高宽比增大而增大。当主梁高度从跨中截面处的300cm逐渐增大到悬臂根部的590cm后，截面阻力系数的差异达到29.43%，因此，在变截面箱梁桥静风稳定性计算中，有必要分段考虑不同高宽比下主梁截面的气动力系数。

进一步可知，对于箱型主梁截面而言，随着主梁高宽比的增大，主梁截面附近的气动绕流会发生一定改变，导致主梁的阻力系数、升力系数和力矩系数绝对值增大。其中高宽比的变化对主梁气动阻力系数和气动升力系数的影响较大，对主梁力矩系数的影响较小。同时，主梁高度的增大进一步引起迎风面特征尺寸的增加，导致作用在主梁上的风荷载显著增加，在后续有必要对不同高宽比的主梁截面气动绕流特性开展研究。

2 风攻角的影响

选取跨中主梁截面(H=300cm)和悬臂根部截面(H=590cm)开展不同风攻角对气动力系数的影响分析，其中风轴坐标系下三分力系数随攻角变化规律分别如图4和图5所示。

由图4和图5可知，在两种不同主梁高度的模型下，桥梁气动力系数随着风攻角的变化趋势基本一致，可以看到主梁的阻力系数CD均为正值，而且其大小随着风攻角绝对值的增大而增大。随着风攻角从-6°增大到+6°，主梁升力系数CL由负值变为正值，即攻角为负角度时，桥梁升力系数为负值，风攻角为正角度时，桥梁升力系数为正值。主梁阻力系数和升力系数随着攻角变化的变化量较大，而风攻角对主梁力矩系数的影响较小。

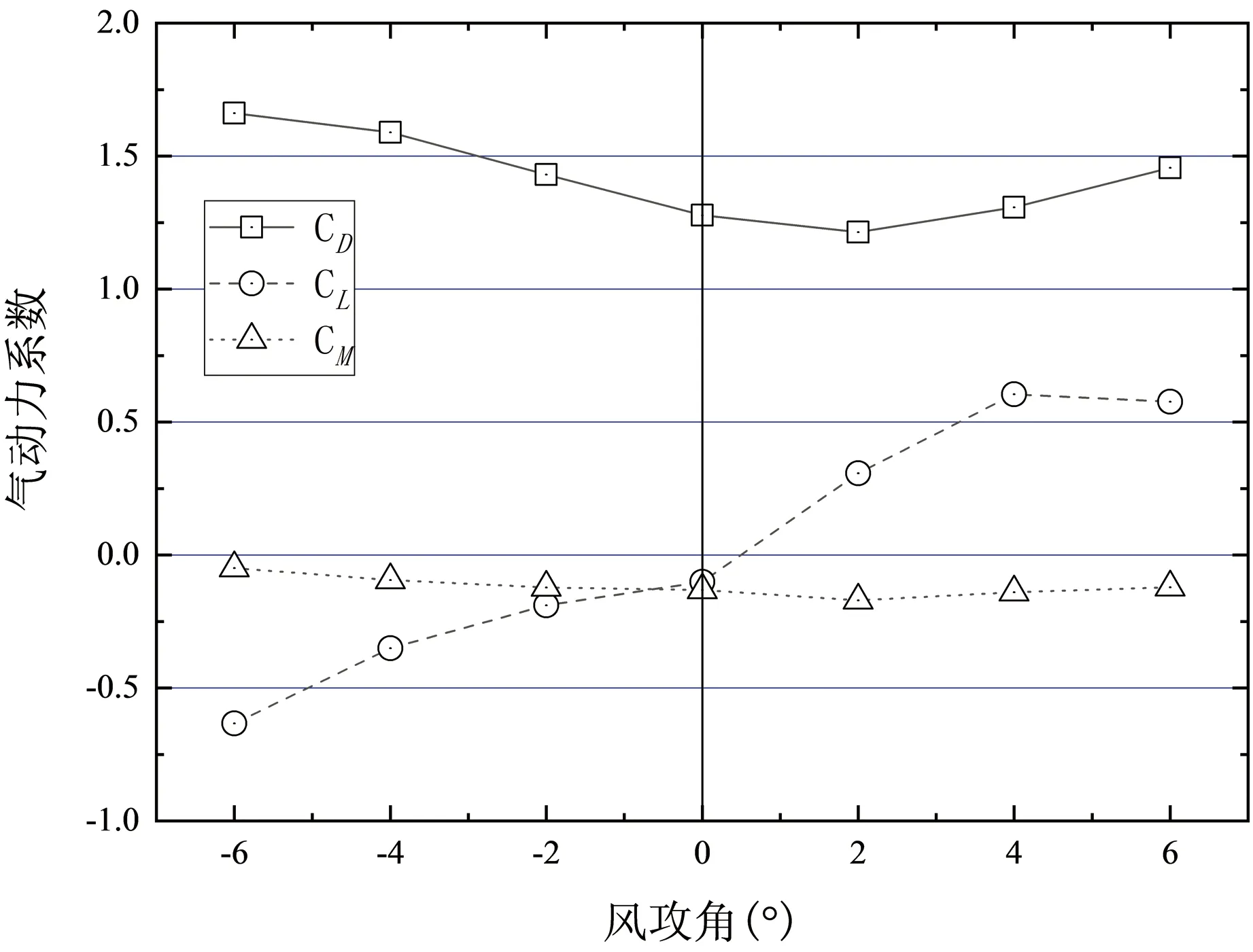
图4 跨中截面三分力系数曲线(H=300cm)

图5 悬臂根部截面三分力系数曲线(H=590cm)

当主梁断面为跨中截面(H=300cm)时，0°风攻角下主梁的升力气动系数为负值，需要对其流场特性进一步开展研究。主梁的力矩系数CM在所有风攻角工况内均为负值，其绝对值大小基本上随着攻角的增大而减小，即主梁力矩系数基本在0°风攻角附近出现最小值。

3 不同高宽比主梁断面的流场分布研究

为了分析不同高宽比桥梁断面气动绕流特性的变化，进一步对主梁截面所处的局部流场进行分析，0°攻角下不同高宽比主梁截面的流线图及压力云图如图6-图9所示。

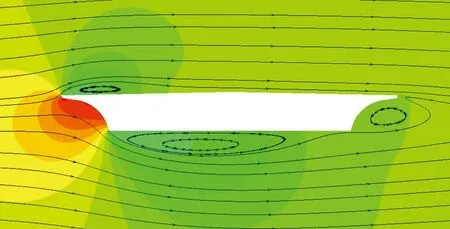
图6 主梁断面流线及压力云图(H=300cm)

图7 主梁断面流线及压力云图(H=395cm)

图8 主梁断面流线及压力云图(H=495cm)

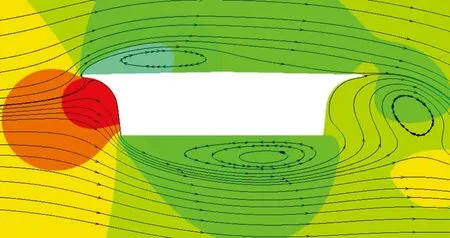
图9 主梁断面流线及压力云图(H=590cm)

由图6-图9可知，来流风经过桥梁上游处的上翼缘后发生分离，在主梁上方、下方及后方位置处产生了多处旋涡。随着高宽比的增加，主梁上方的旋涡尺寸逐渐增大，并向主梁中间移动。当主梁高度H=300cm时，主梁上方旋涡尺寸较小，而下方尺寸较大，且下方旋涡分离后又重新附着在了主梁下表面，这是导致上节中0°风攻角下该截面的升力气动系数为负值的原因。主梁下方的旋涡尺寸同样随着高宽比的增加而增大，且逐渐远离主梁下表面，向下游方向移动。

特别的是，当主梁高度H=495cm时，在主梁后下方生成了一个小漩涡，是主梁下方旋涡的一部分。主梁后方的旋涡随着高宽比的增大而逐渐向下游方向移动，并生成了两个旋涡，而当高宽比增大到一定值后，两个旋涡变成了一个旋涡，且远离了主梁后方。由结果可知，随着高宽比的增大，主梁断面逐渐呈现出了钝体的气动特性。

4 结论

本文通过建立某大跨度变截面预应力连续箱桥主梁截面的CFD分析模型开展数值模拟，讨论了不同高宽比和风攻角下主梁截面的气动力系数，进一步研究了变截面主梁周围的气动绕流特性，得出了以下结论：

(1)不同高宽比的主梁三分力系数差别较大，跨中截面和悬臂根部截面的阻力系数分别为1.278和1.811，两者相差29.43%。因此，在变截面箱梁桥的静风稳定性计算中，应该考虑不同高宽比下主梁气动力系数的变化。

(2)来流风攻角对主梁截面的三分力系数影响较大。随着风攻角从-6°增大到+6°，主梁升力系数随着风攻角的增大而逐渐从负值变成正值。主梁气动阻力和力矩系数均随着风攻角绝对值的增大而增大，但主梁阻力系数和升力系数随着攻角变化的变化量较大，而风攻角对主梁力矩系数的影响较小。

(3)随着主梁高宽比的增加，主梁上方旋涡尺寸逐渐增大，并向主梁中间移动，流体重新附着在主梁上的横向距离增大；主梁下方的旋涡尺寸同样逐渐增大，且向远离主梁下表面，向下游方向移动；主梁背风侧旋涡则逐渐沿下游方向移动，主梁截面逐渐呈现出了钝体的气动特性。