使用动态规划结合有限元应力场对湿陷性土坝进行瞬态稳定性分析

2022-10-29邓伦宇

四川水利 2022年5期

邓伦宇

(南昌市防洪排涝工程事务中心，南昌，330009)

0 引言

小型湿陷性土坝常见于我国半干旱地区[1]。这些水坝的建造是为了提供一个水库，可以在短暂的雨季积累降水，在漫长的旱季为农业和公共用水提供用水[2]。由于缺乏合适的压实设备和水，这些大坝中存在一些在干燥的最佳亚稳态条件下压实很差的情况[3]。因此，在第一次蓄水过程中，压实土在湿润状态下会发生较大的坍塌和抗剪强度损失。破坏机制通常以上游边坡的楔状破坏为特征，并结合下游边坡的管道破坏。

本文对某典型小型湿陷性土坝进行了稳定性分析。为了进行分析，将动态规划法(DPM)代码SAFE-DP与全耦合流体力学有限元代码COUPSO相结合。假设使用的本构参数从状态表面和非线性完美塑性弹性行为获得，对土坝的上游和下游的斜坡进行了研究。本文介绍了对滑移面形状和位置的演变以及施工结束、快速蓄水池充填和充填后阶段安全因素演变的分析。此外，在文中讨论了DPM的性能。

1 动态规划法

动态规划法(DPM)是线性泛函最大化和最小化的通用方法[4-5]。Baker(1980)介绍了DPM在边坡稳定性分析中的应用。Baker(1980)提出的程序使用了DPM，同时保留了关于层间力的假设。后来，几位研究人员提出了Baker程序的扩展，使用了有限元应力场。

1.1 优化过程

DPM是一个通用的优化程序，可用于确定故障机制和相应的最小安全系数[6]。如图1所示，滑移面由一系列由阶段和状态点定义的线性段形成。安全系数Fs可以以离散形式定义，如下所示：

(1)

图1 用动态规划进行稳定性分析的解析方案

其中，n为段数；τfi为沿i段土体的抗剪强度；△Li为i段的长度；τi为沿段i作用剪应力。由于该方法不适用于非加性泛函，所以不能用DPM最小化泛函Fs。Fs的最小化可以通过最小化以下辅助泛函来实现：

(2)

式中，G的最小化是利用最优原则来实现的。根据最优性原则，后一阶段最优函数Hi+1(j)是前一阶段最优函数Hi(k)的函数，如下所示：

Hi+1(j)=min[Hi(k)+DGi+1(j,k)]

(3)

式中，DGi+1(j，k)是连续阶段在两个状态点之间通过的“成本”。初始阶段的最优函数值(H1(k)=1)在任何状态点都等于零。在最后阶段，最优函数对应于G的最小值，如下所示：

(4)

其中，Ri为沿线段i的阻力；Si为沿线段i的剪切力。一旦确定了最后阶段的最优函数，通过连接从最后阶段追溯到最后阶段的最佳状态点，找到最佳路径。临界滑动面对应于最佳路径。

由式(1)可以看出，优化过程是非线性的。对于给定的容错性，必须假定F的初始值，并且必须重复计算，直到F的值收敛。

图2 连接两个状态点的线段上的最佳变量

1.2 计算在分析中使用的应力

可根据抗剪强度包络线并使用应力状态变量定义沿任何段“i”的抗剪强度。可以使用有限元方法获得两个正交平面在x和y方向(σx、σy和τxy)上的应力状态场。根据σx、σy和τxy定义的应力状态场，可使用以下方程式计算作用于以θ角倾斜的任何管段上的法向应力σθ和剪切应力τθ(见图2)：

σθ=σxsin2θ+σycos2θ-τxysin2θ

(5)

(6)

2 控制水力学土壤行为的耦合微分方程

用于湿陷性坝稳定性分析的应力状态场已使用有限元程序COUPSO计算。该程序COUPSO以完全耦合的方式求解二维平面应变条件的平衡方程和水守恒方程。分析非饱和土的行为，饱和条件是一种特殊条件。本构模型和参数基于状态表面概念和非线性弹性、理想塑性行为。使用应力状态变量定义孔隙比、饱和度、水力传导率和泊松比的状态表面以及剪切强度包络线；即净总应力(σ-ua)和基质吸力(ua-uw)。基于空气相是连续的并与大气接触的假设，空气流动被忽略。

2.1 静力平衡

通过考虑作用在代表性土壤元素体积(REV)上的力的平衡，可以获得控制静态平衡的偏微分方程。微分方程中的应力可以使用应力-应变关系(广义胡克定律)替换为应变。分别针对x和y方向获得以下等式：

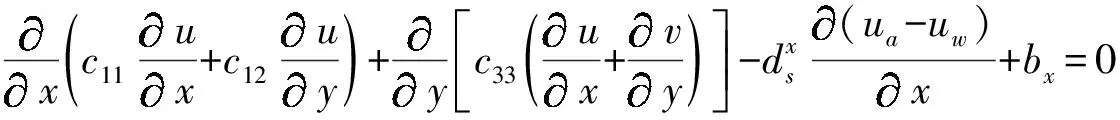
(7)

(8)

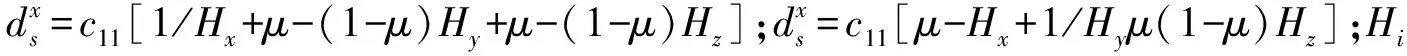
2.2 水质量守恒

考虑水在土壤中的进出流动，利用水流的达西定律，可以得到水的二维流动和守恒的偏微分方程。得到的方程如下：

(9)

其中，βw1=(m1w/m1s)；βw2=m2w-(m1wm2s/m1s)；m1w=[2(1+μ)/Ew]；m2w=[1/Hw-(E/H)/Ew]；m1s=2(1+μ)(1-2μ)/E；m2s=[1/Hx+1/Hy+2μ/Hz]；Ew为相对于净平均应力变化的水相体积模量，σ-ua；Hw为相对于基质吸力变化的水相体积模量；εv为总体积应变；为发散算子；k为导水率；γw为水的容重；y为高度。

3 小型亚稳态大坝稳定性分析

所分析的假设土坝代表了我国半干旱地区遇到的典型小型亚稳坝。以下章节将介绍分析中使用的土壤特性、问题几何、初始和边界条件以及稳定性分析的结果。本文给出的结果将集中于使用SAFE-DP程序和获得的应力状态有限元场获得的稳定性分析结果。

3.1 土壤性质

本研究使用三轴仪、测力仪和直剪仪，在有无基质吸力控制的情况下，对土壤性质进行了实验测定。

此处总结的土壤特性基于在单调润湿路径下进行的测试，基质吸力从370到0kPa分阶段变化。已有学者提出了适合实验结果的数学函数，这些函数基于应力状态变量(σ-ua)和(ua-uw)。所采用的数学函数能够拟合获得的实验数据，是连续的，并且具有连续的导数。用于定义空隙率e和饱和度S状态曲面的函数如下：

(10)

(11)

其中，eu=0.7697-0.0073ln(σm-ua)，为崩前阶段的孔隙比；ef=0.752+{[-0.142/(1+(σm-ua)/75)-3.5]}，为塌陷后阶段的孔隙比；b=39.01(σm-ua)-0.6103，是控制坍塌相形状的参数；c=0.00094(σm-ua)2+0.07465(σm-ua)+11，是塌陷中期基质吸力的对应参数；(σm-ua)为净正常平均应力；S0=0.375，为初始饱和度；d=0.9769，为参数，定义了塌陷阶段润湿曲线的斜率；cm=20，是塌陷阶段中期基质吸力对应的参数。

水导率的实验结果采用以下函数拟合：

(12)

其中kp=-1.4×10-7+6.26×10-8ln(σm-ua)，表示总平均应力变化时导率的变化；ψcr=3.0，为进气量；λ=2.1，为经验常数。

剪切强度包络线利用具有基质吸力控制的直接剪切仪获得。由于较高的吸力值的贡献被发现是可以忽略的，所以基质吸力值在100kPa到0kPa之间变化。用以下函数表示剪切强度包络线：

τff=a1+b1(σ-ua)+c1(ua-uw)
+d1(σ-uu)(uu-uw)p

(13)

其中，a1=5.0，是有效内聚截距；b1=0.1944，为有效摩擦角的正切；并且c1=0.3238、d1=0.09319和p=4.307×10-7是拟合参数。

3.2 几何问题、边界和初始条件

图3显示了用于分析施工、水库快速填充和后填充阶段的几何问题和有限元网格。施工阶段使用5层进行模拟，并考虑线性弹性行为，μ=0.3和E=5800kPa。施工阶段唯一的作用荷载是与土壤单位重量相对应的体荷载(γnat=14.75kN/m3)。下边界的边界条件对应于刚性基础，没有相对滑动(x和y方向没有位移)。施工阶段的孔隙水压力变化被忽略。

假设370kPa的基质吸力和施工阶段模拟获得的应力为快速水库蓄水阶段模拟的初始条件。通过零检验获得初始基质吸力值后，采用相同的基质吸力值和从快速水库蓄水分析中获得的应力作为蓄水后阶段模拟的初始条件。填充后分析假设的水流边界条件如图3所示。在快速蓄水过程中，不允许出现水渗透和孔隙水压力变化。时间离散包括17d的初始时间步，然后是0.2d的较小时间步。为了防止数值不稳定，需要较大的初始时间步长。

图3 大坝横截面、有限元网格和边界条件

3.3 结果与讨论

图4和图5分别为上、下游边坡临界滑面形态和位置的演化。可以看出，施工阶段结束时，上下游边坡的临界滑移面和安全系数是一致的，且与预期一致。

水库快速填筑阶段后上游边坡的临界滑动面略深于施工阶段结束时的临界滑动面。这是由于水库荷载导致上游边坡附近的围压较高。水库荷载的另一个影响是，由于摩擦产生的较高剪切强度，安全系数显著增加。考虑到水库荷载引起的围压增加随上游边坡距离的增加而减小，施工结束和快速填筑阶段获得的相关结果是正确的。水库快速蓄水阶段后，下游边坡的临界滑动面和安全系数没有发生任何显著变化。

图4和图5还显示了充填后阶段的临界滑动面。湿润锋提前导致大坝不均匀沉降。因此，应力分布会发生变化，以适应此类沉降。水库蓄水后58d内，上游临界滑动面相对较浅。这一结果与湿润锋的位置以及该区域剪切强度的相应降低一致。在此阶段，下游边坡的临界滑动面没有显著变化。

水库蓄水后98d的上游临界滑动面比前一个滑动面(58d)更深。滑动面的形状与圆形相差很大。临界滑动面的加深和安全系数的降低是由于湿润锋的进一步推进。下游斜坡再次受到湿润锋的显著影响，湿润锋仍然局限于上游斜坡附近的区域。

图4 上游边坡稳定性分析结果

图5 下游边坡稳定性分析结果

水库蓄水后138d内获得的上游临界滑动面对应于大坝理论失效的阶段(Fs<1)。随着湿润锋的推进，获得的临界滑动面比之前的表面更深。滑动面形状明显偏离圆形，由刚性坝基础的位置控制。未观察到下游边坡安全系数和临界滑动面的显著变化。由于不均匀沉降引起的应力重新分布，安全系数几乎没有降低。图6总结了上述安全演变因素。