基于CFD方法的矩形窄缝通道内过冷流动沸腾模型研究
2022-10-29李林峰王明军田文喜秋穗正苏光辉
刘 凯,李林峰,王明军,*,章 静,田文喜,秋穗正,苏光辉
(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;2.西安交通大学 核科学与技术学院,陕西 西安 710049)
板型燃料元件具有活性区比功率大、结构紧凑等优势,在众多研究堆、材料辐照堆中获得了应用。其堆芯冷却剂通道截面形状为矩形窄缝,具有宽高比大的几何特征,在发生过冷沸腾时,汽泡运动行为将受到高度方向上更陡峭的速度分布的影响而发生改变。
在加热壁面上的汽泡行为中,汽泡滑移现象受到很多学者的关注。Thorncroft和Klausner[1]对竖直通道中冷却剂FC-87的沸腾换热系数进行了测量,结果表明,向上流动沸腾的换热系数显著高于向下流动工况,分析认为向上流动时壁面附近汽泡的滑移运动增强了换热。Li等[2]进行了运行压力0.1 MPa、高2 mm的窄矩形通道内竖直向上的流动沸腾实验,同样观察到了频繁的汽泡滑移。Yuan等[3-4]在运行压力0.3~1 MPa工况的2 mm高窄缝通道实验中观察到了汽泡滑移现象,并对滑移汽泡的瞬态换热项建模,结果表明滑移汽泡对换热的贡献可达静止汽泡的10倍。Yoo等[5]使用热成像记录了滑移汽泡的影响面积,结果表明汽泡滑移过程中影响面积与汽泡直径相关。
计算流体力学(CFD)目前已广泛应用于工程模拟中[6-7],包括棒束通道的两相沸腾模拟[8-9],但对窄矩形通道内沸腾分析时往往不能采用已有模型和关系式,因此,开发适用于矩形窄缝通道的沸腾模型具有相当的重要性。
本文针对矩形窄缝通道中的汽泡滑移对沸腾换热的影响,构建包含滑移热流的壁面热流分配模型,并建立机理性的汽泡受力模型和滑移模型计算汽泡脱离直径、浮升直径和滑移距离等辅助参数,开发一套适用于矩形窄缝通道内竖直向上流动沸腾的壁面沸腾模型。选用Nuthel窄缝通道沸腾实验进行数值模拟,通过对比壁面过热度的计算结果与实验结果,验证本文模型对矩形通道内中低压过冷沸腾流动换热特性模拟的有效性。
1 数学物理模型
本文基于欧拉两流体六方程模型,分别对气、液两相建立质量、动量、能量守恒方程,并考虑相间相互作用,引入相间质量、动量、能量交换模型[10]。相间动量交换中的作用力包括曳力和非曳力,非曳力又包含升力、湍流耗散力、壁面润滑力,相间质量和能量交换包括近壁面沸腾换热和相界面上的蒸发、冷凝过程。
此外,本文考虑汽泡滑移现象对沸腾换热的影响,构建包括滑移热流的壁面沸腾模型,并建立机理性的辅助模型计算相关汽泡关键参数,以对模型整体进行封闭,形成壁面热流密度和壁面温度的计算关系。
1.1 考虑汽泡滑移的壁面沸腾模型
Kurul和Podowski[11]提出的RPI壁面沸腾模型广泛应用于流动沸腾计算,该模型仅考虑了汽化核心当地的汽泡行为,认为壁面热流包括对流换热、蒸发、淬灭热流3部分。
本文针对窄矩形通道中的汽泡滑移行为,采用以下过程描述汽泡生长的周期,如图1所示。汽泡在脱离汽化核心后将垂直于壁面浮升或平行于壁面滑移。滑移过程中由于其与壁面接触处的微液膜蒸发,并与其他汽化核心处汽泡融合,汽泡直径持续增大,当达到一定值后汽泡浮升进入主流区域。该过程中,汽泡离开汽化核心处、开始滑移时的直径为脱离直径dd,汽泡垂直壁面运动、远离壁面并进入主流时的直径为浮升直径dl。
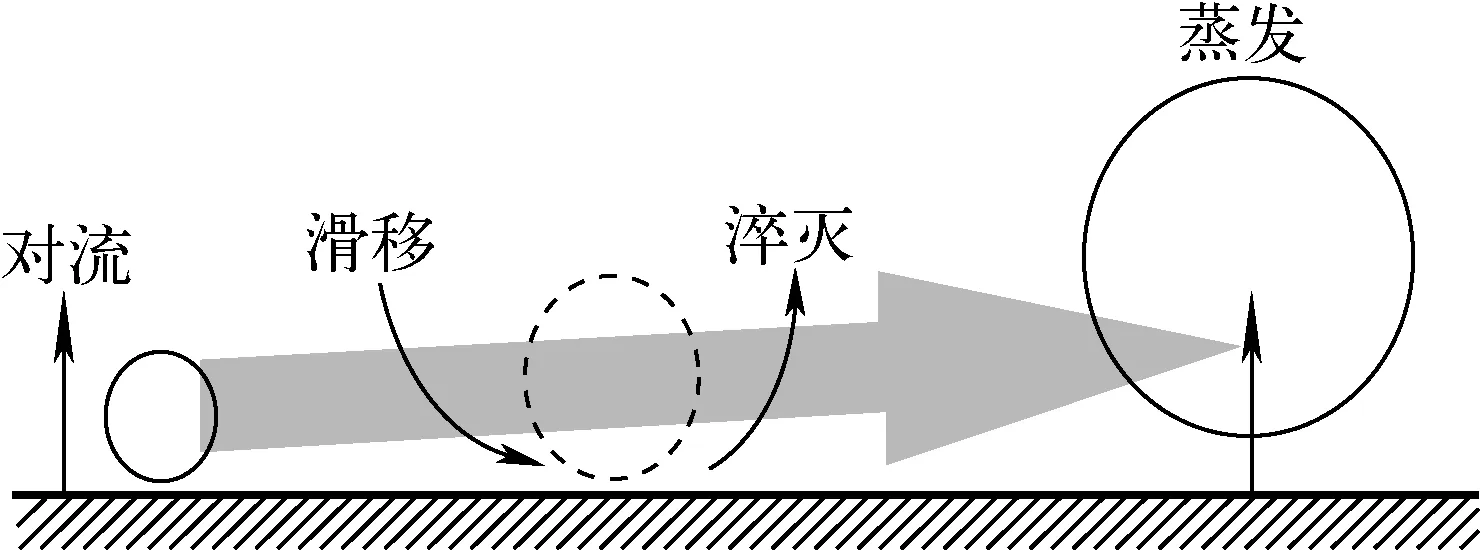
图1 壁面沸腾模型对汽泡生长周期的描述Fig.1 Description of bubble period by wall boiling model
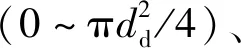
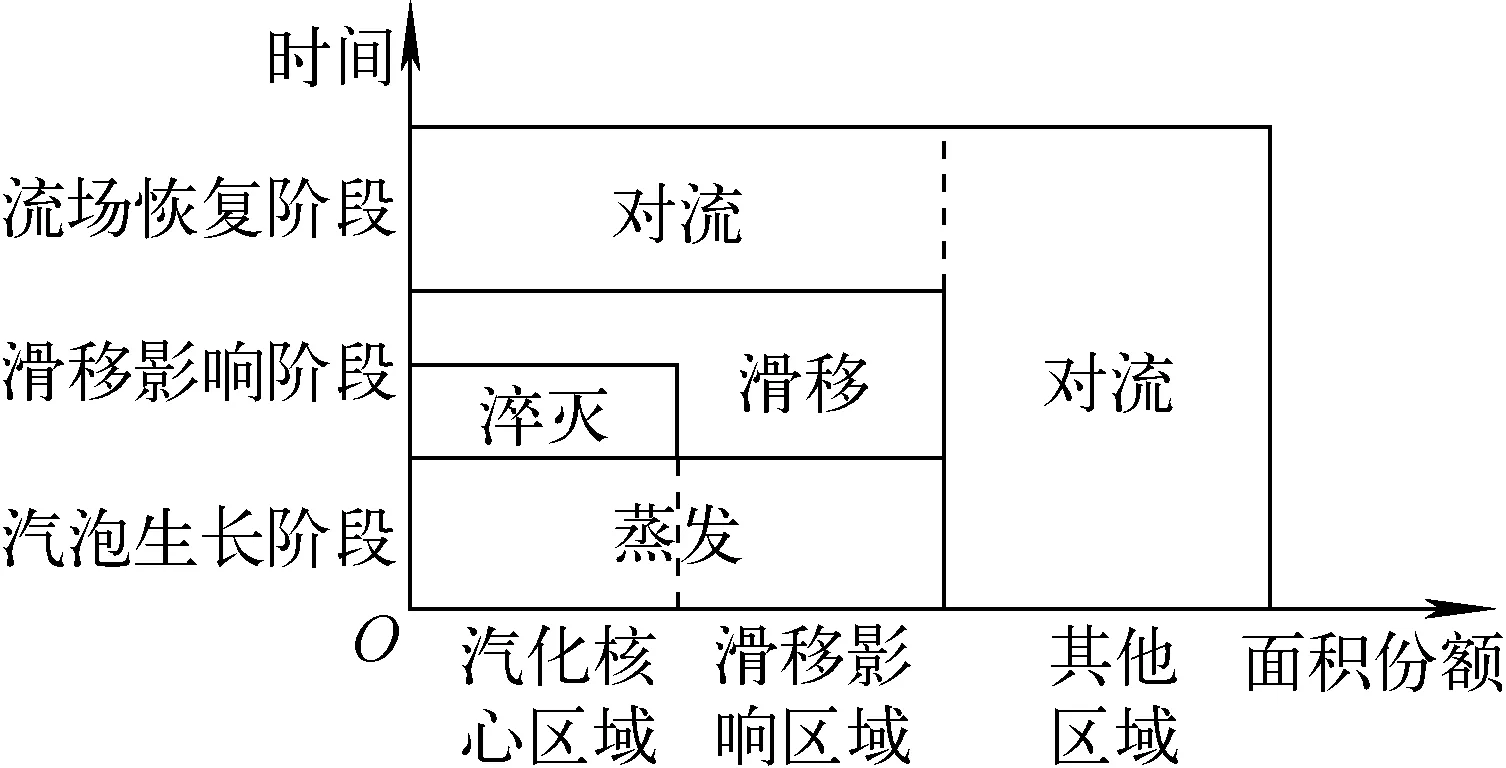
图2 壁面沸腾模型对总热流的分配Fig.2 Distribution of total heat flux by wall boiling model
1) 汽泡生长阶段(0~tg,其中tg为汽泡生长时间)中,汽化核心区域的相变和滑移影响区域的微液层蒸发计入蒸发热流。
2) 滑移影响阶段(tg~t*,其中t*为换热增强效果消失时刻)中,在汽化核心区域,固体侧由淬灭热流主导,而流体侧为由于汽泡扰动的滑移热流。在滑移影响区域,由汽泡滑移的扰动带来的额外换热增强计入滑移热流。
3) 在流场恢复阶段(t*~1/f,其中f为汽泡脱离频率)中,单相对流换热重新占据主导,而其他区域在整个汽泡周期中仅存在单相对流换热过程。
据此,本文所开发的壁面沸腾模型将壁面总热流qt分为4项热流,分别为单相对流热流qc、蒸发热流qe、淬灭热流qq和滑移热流qs,其表达式为:
qt=qc+qe+qq+qs
(1)
蒸发热流的表达式为:
(2)
式中:hfg为汽化潜热;f为汽泡脱离频率;N*为汽化核心密度。
由于汽泡滑移扰动,来自主流区域的较低温度流体补充汽泡原先占据的位置,并与过热壁面接触换热。将其简化为半无限大区域冷却平板瞬态导热问题,则壁面瞬态热流表达式为:
(3)
式中:kl为液相导热系数;Tw为壁面温度;Tl为流体温度,此处取液相近壁面温度;ηl为液相热扩散率;τ为瞬态过程时间,即滑移热流的影响时间,从汽泡滑移开始至换热增强效果消失,即瞬态导热系数与单相对流换热系数相等时为止,记作0~τ*。令瞬态导热系数与单相对流换热系数相等,得到滑移影响时间表达式:
(4)
式中,hfc为当地流动恢复时的单相对流换热系数。
考虑汽泡影响时间和影响面积,积分可得滑移过程中的瞬态导热热流,即滑移热流:
(5)
式中,asl为汽泡的影响面积。
单相对流热流根据近壁面对流换热系数hfc计算:
qc=hfc(Tw-Tl)·(1-aslN*+aslN*(1-τ*f))
(6)
Gilman等[12]认为,汽泡生长时底部存在高温干斑;当汽泡脱离后这部分壁面显热会释放到流体中,组成新的淬灭热流。具体地,认为汽泡底部干斑呈圆形,其直径为汽泡脱离直径的1/2。干斑下的半球形高温区较其他区域温度高ΔTh,淬灭点与周围壁面的温差约为3 K。因此淬灭热流表达式为:
(7)
1.2 辅助模型
1) 汽泡受力模型
由于现有经验关系的适用范围有限或未区分汽泡脱离直径和浮升直径,本文建立汽泡受力模型计算汽泡脱离直径和浮升直径。采用Sugrue和Buongiorno[13]推荐使用的受力表达式和系数组合列于表1,其在反应堆典型应用场景内得到了一定的验证。1个倾斜壁面上汽泡受力情况如图3[13]所示,图中x方向平行于壁面为流动方向,y方向垂直于壁面为浮升方向,θ为壁面水平倾角。

表1 汽泡所受作用力表达式Table 1 Expression for force acting on bubble
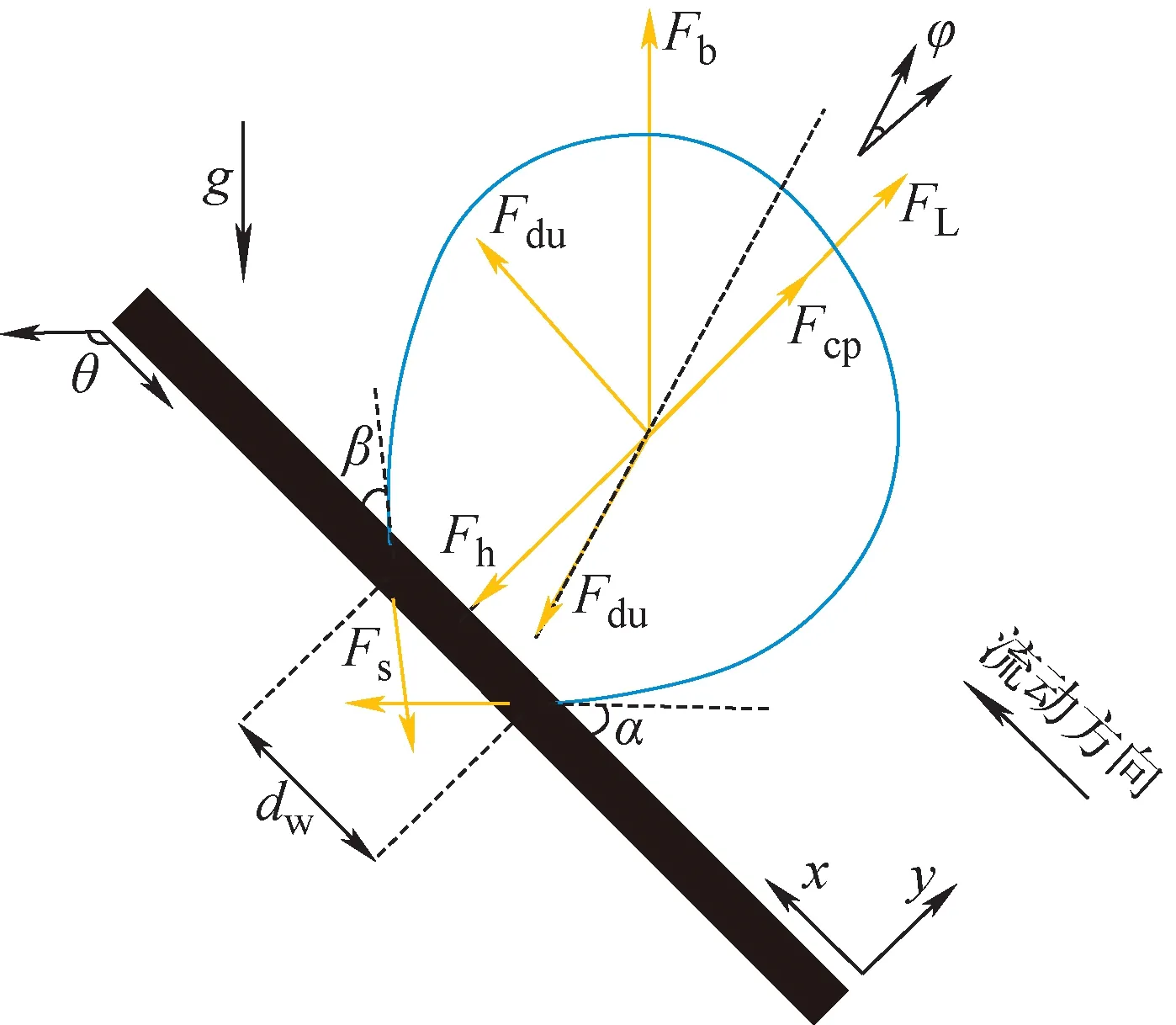
图3 单个静止汽泡受力示意图Fig.3 Diagram of force on single static bubble
对于静止汽泡,两方向上的合力分别为:
(8)
式中:θ为加热壁面的倾角;φ为汽泡偏向流动方向的倾角,一般假设汽泡生长方向与壁面法向的夹角为π/15。当ΣFx>0时,汽泡达到dd并平行于壁面运动;当ΣFy>0时,汽泡达到dl并垂直于壁面运动。
2) 汽泡滑移模型
通过滑移过程中汽泡生长方程计算汽泡滑移时间,进而得到汽泡滑移距离,本文使用Maity[14]拟合的汽泡直径关系式计算,如下:
(9)
式中:d1和d2分别为汽泡滑移起始和终止时的直径;τs为滑移时间;Jasup和Jasub分别为壁面过热度和液相过冷度雅各比数;Reb为以汽泡平均直径、汽泡滑移速度计算的雷诺数。
根据Basu[15]对滑移汽泡的建模,在汽泡由上一个汽化核心与当地汽泡融合并向下一个汽化核心滑移过程中,汽泡直径由dN-1不断增大,在该过程中判断汽泡是否脱离即可得到汽泡滑移距离:
l=Nms+ldN-1~dl
(10)

滑移过程中单个汽泡的影响面积为:
asl=l(dd+dl)/2
(11)
此外,当浮升直径小于汽泡脱离直径时,汽泡将不发生滑移而直接浮升。此时,汽泡行为实际上与RPI模型的描述相同,汽泡影响面积按下式计算:
(12)
式中,K为影响范围因子。根据Valle和Kenning等[16]对汽化核心处汽泡的观测分析使用以下公式计算:
(13)
3) 汽泡脱离频率模型
汽泡脱离频率使用Cole[17]关系式计算,其表达式如下:
(14)
式中,g为重力加速度。
4) 汽化核心密度模型
汽化核心密度使用Lemmert-Chawla[18]公式计算:
Nw=[n0(Tw-Tsat)]m
(15)
式中,参考密度n0和指数m分别取210和1.805。根据汽泡滑移距离,汽泡融合个数可以按l/s估计,则修正后的汽化核心密度为:
(16)
2 实验模拟与结果分析
2.1 实验介绍
选取西安交通大学反应堆热工水力研究室(Nuthel)梁振辉[19]的过冷沸腾实验进行模型验证。实验回路主要由屏蔽泵、稳压器、预热器、实验段、直流加热电源、冷却器和相应的数据测量系统组成。实验段为竖直放置的窄矩形通道,宽度为50 mm,高度为1.5 mm和2.5 mm。实验段的加热方式为电加热,有效加热长度为0.8 m。工质是去离子水,实验压力范围0.5~5 MPa,入口过冷度范围50~80 K,质量流量13.3~266.7 kg/(m2·s),热流密度范围10~300 kW/m2。实验段外壁面上点焊热电偶,测量外壁温度计算得到内壁温度。焊点选择在矩形壁面宽边的中心线位置,布置间距为100 mm。实验段参数列于表2[19]。本文选取截面尺寸为2.5 mm×5 mm通道内4组不同压力下的实验工况进行模拟,具体运行参数列于表3。
2.2 模拟方法
1) 计算区域选取
由于窄缝通道具有较大的宽高比,除接近边缘处,在宽度方向上参数分布基本均匀。为降低计算量,通过选取通道中心的纵截面进行二维模拟的方法简化。为验证该简化的合理性,对工况Nuthel-659分别进行三维和二维计算,计算条件保持一致。
三维与二维计算结果的对比如图4所示,可见,二维与三维计算得到的中心纵截面上的壁面温度计算结果相差不大;除边角非加热区域外,三维计算结果的空泡份额分布在宽度方向上分布均匀。因此采用通道中心纵截面进行二维模拟的简化方法可行。
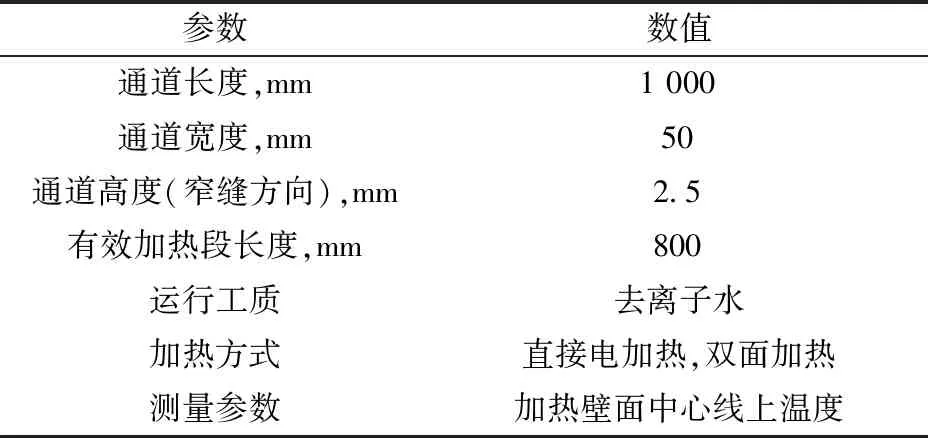
表2 Nuthel窄缝通道沸腾实验段参数Table 2 Parameter of Nuthel narrow rectangular channel boiling experiment section

表3 模拟工况运行参数Table 3 Operating parameter of simulation case
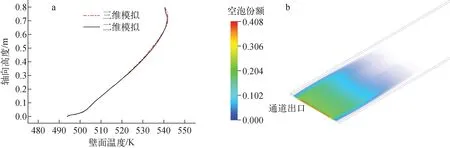
a——壁面中心线温度分布对比;b——三维模型出口处空泡份额分布图4 二维模型有效性验证Fig.4 Validation of 2D model
2) 网格划分
使用四边形结构化网格对矩形流道进行空间离散。为进行网格敏感性分析,划分7套不同网格,具体划分方式和计算结果列于表4,测试工况是Nuthel-627号。
对比网格#1、#2、#5和#7的结果可知,高度方向均匀划分5个控制体时计算发散,将节点分布改为非均匀布置,使近壁面网格厚度为0.25 mm时则计算收敛;当划分10或15个控制体时结果较为接近,但后者壁面网格y+值低于10,第1层节点落在速度过渡层内,不适用标准壁面函数。因此,计算中高度方向划分10个控制体。对比网格#3~#7的结果可知,长度方向上网格数量对壁面过热度影响较小。综上,选取#3网格对Nuthel实验进行模拟。

表4 网格敏感性分析Table 4 Grid sensitivity analysis
3) 材料物性
计算中使用运行压力下的水物性。由于实验中入口过冷度较高,因此液相物性使用入口温度和饱和温度两点线性插值方法确定。过冷沸腾中气相温度几乎维持在饱和温度,因此气相物性使用饱和状态下的水蒸气物性。
本文模型中的淬灭热流考虑了壁面材料的影响,而两实验中沸腾区壁面材料均为钢,因此取不锈钢的物性典型值,密度8 000 kg/m3,比热500 kJ/(kg·K)。
4) 边界条件
入口边界为流量入口,给定液相质量流量和温度,气相体积份额为0;出口为压力出口,表压为0。入口和出口非加热段为绝热边界;认为加热功率均匀分布,即加热段为均匀热流密度边界。
2.3 计算结果分析
1) 壁面过热度和近壁面空泡份额
分别使用本文模型和RPI模型进行模拟,得到壁面温度和近壁面空泡份额的计算结果如图5所示。
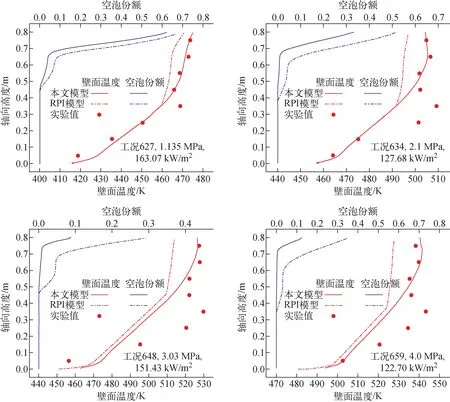
图5 壁面温度和近壁面空泡份额计算结果Fig.5 Calculation results of wall temperature and near-wall void fraction
由于过冷沸腾阶段的高换热效率,壁面温度沿流动方向出现拐点,壁温上升减缓,出现一段壁温平台,近壁面空泡份额相应上升。通道壁面自沸腾起始点的平均过热度计算结果与实验结果的对比列于表5,可见RPI模型的计算结果偏低,而本文模型计算得到的沸腾区过热度与实验值符合良好,对壁面过热度的预测精度较高。此外,本文模型近壁面空泡份额的计算值较低。
单相对流区的壁温计算结果存在较大偏差,导致沸腾起始点的预测不准确。分析认为偏差主要由热效率不稳定造成:单相对流区的壁面温度与壁面热流密度约为线性关系,预先通过单相换热实验测量的热效率可能在沸腾实验过程中改变,因此模拟中的给定热流与实验条件存在偏差。而在过冷沸腾区域热流偏差的影响较小,其原因为:过冷沸腾区壁面过热度与壁面热流约为0.25~0.3次幂函数关系,例如Jens-Lottes公式中ΔTsup∝q0.25,相同的热流偏差在过冷沸腾区域引起的壁面过热度误差较小,仅为单相区域的2.4%。
2) 热流密度分配
热流密度分配的计算结果如图6所示。本文模型的计算结果中,滑移热流和单相对流热流占据主导,蒸发热流份额相对较小。而RPI模型的计算结果中,蒸发热流在通道后段占据主导,单相对流热流和淬灭热流份额都相对较小。
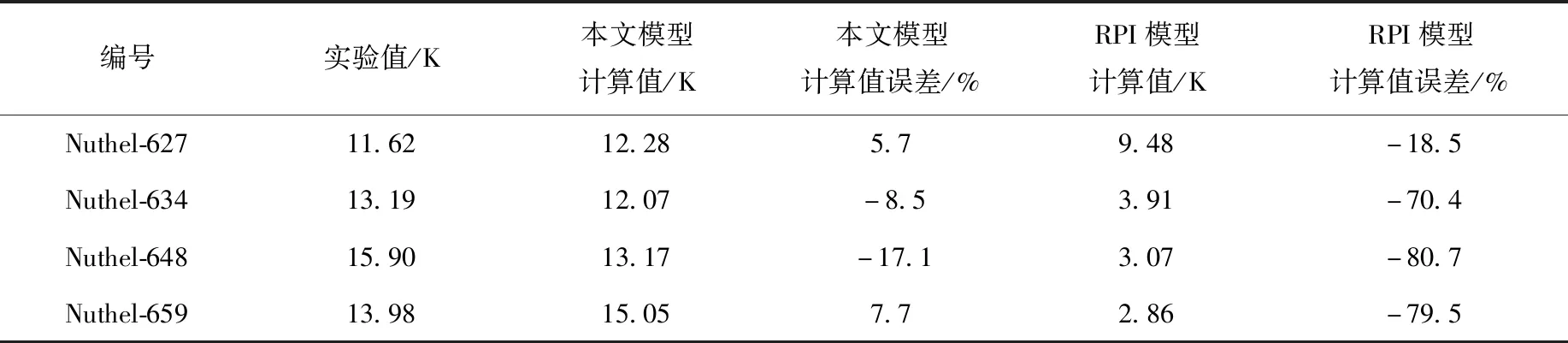
表5 壁面平均过热度计算结果与实验结果的误差Table 5 Error between calculated and experimental results of average superheat of wall
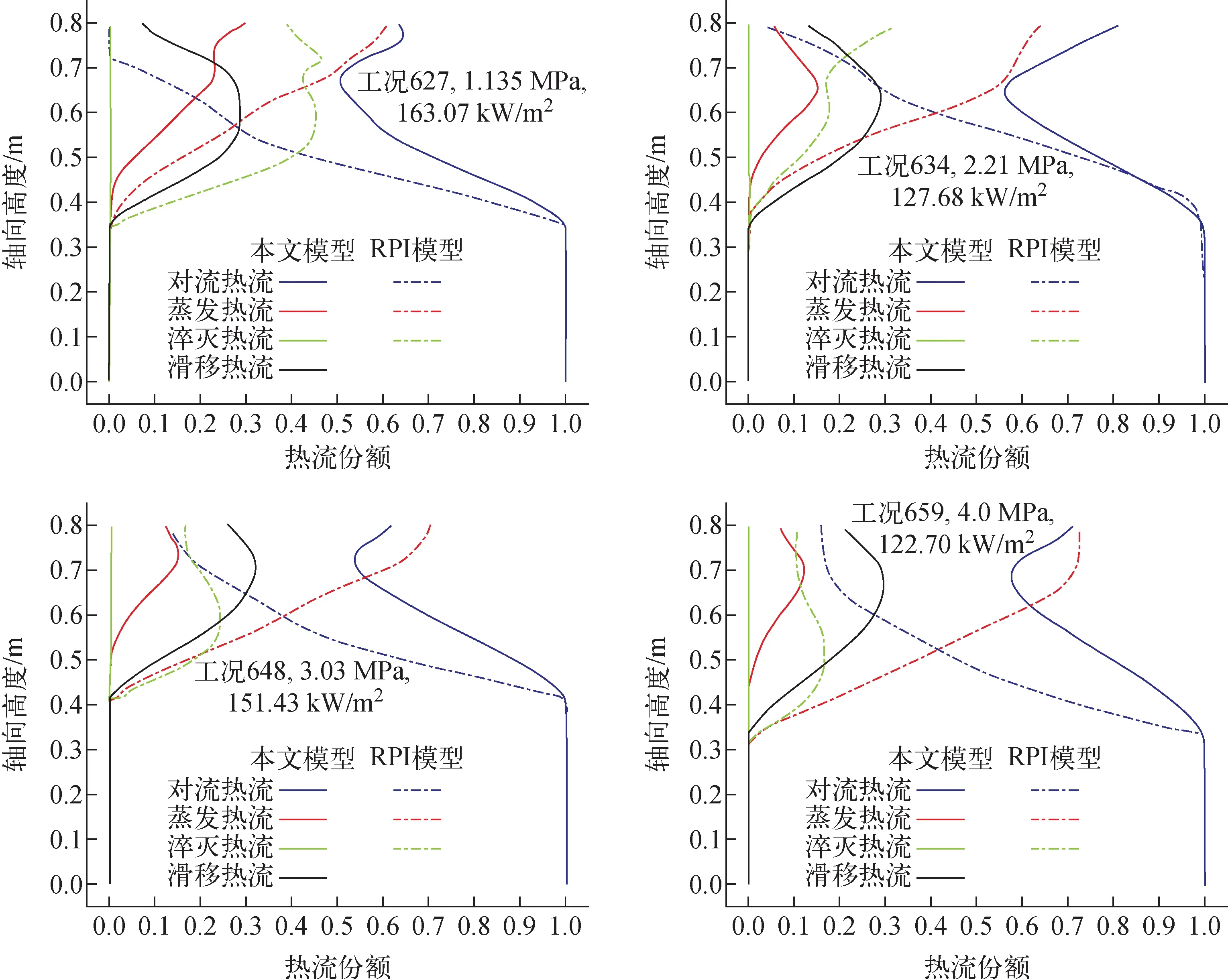
图6 热流密度分配计算结果Fig.6 Calculation result of wall heat flux distribution
本文模型的蒸发热流份额较小,导致近壁面蒸发率较低,因此近壁面空泡份额的计算结果较小。此外,本文模型计算结果中淬灭热流所占份额较小,几乎可以忽略,说明在模拟工况中壁面显热的影响较低。
3 结论
本文针对矩形窄缝通道中的汽泡行为,考虑汽泡滑移现象对沸腾换热的影响,构建了包含滑移热流的壁面热流分配模型,并建立机理性的汽泡受力模型和滑移模型计算汽泡脱离直径、浮升直径和滑移距离等辅助参数,开发了一套适用于矩形窄缝通道内向上流动沸腾的壁面沸腾模型,选用Nuthel窄缝通道沸腾实验的1~4 MPa中低压过冷沸腾工况进行验证,主要结论如下:
1) 本文模型的壁面温度计算结果相比RPI模型较高,模拟工况中沸腾区的壁面平均过热度误差由最大80%降至最大17%,说明滑移热流的引入可以更精确地预测矩形窄缝通道内向上流动沸腾的壁面温度;
2) 本文模型的热流分配计算结果中,滑移热流和单相对流热流份额占据主导,蒸发热流份额较低,蒸发率较低,因此近壁面空泡份额计算结果相比RPI模型较低;淬灭热流所占份额较小,说明在模拟工况中壁面显热的影响较低。
