基于k近邻平均距离的异步航迹关联算法
2022-10-29衣晓,曾睿,2,*
衣 晓, 曾 睿,2,*
(1. 海军航空大学, 山东 烟台 264001; 2. 中国人民解放军92325部队, 山西 大同 037001)
0 引 言
对于分布式多传感器多目标跟踪系统,由于各局部节点独立工作,每个局部节点一般都有多条目标航迹信息,如何判断来自不同局部节点的航迹是否对应同一个目标,即航迹关联,是融合中心需要解决的关键问题之一。而各局部节点配置传感器的采样周期不一致或者开机时机不同,使得融合中心收到的局部航迹往往是异步不等速率的,增加了航迹关联的难度。
对异步航迹关联问题,传统的解决思路是进行时间配准,将异步航迹转换为同步航迹进行处理。常用的时间配准方法有最小二乘法和内插外推法。文献[8]通过伪测量技术,将来自不同传感器的测量值和滤波值重建到一个合适的时间点,再利用经典分配算法实现异步关联。文献[9]利用匀角速度变换率插值法,将多传感器的时间对齐,再用局部寻优方法进行关联。文献[10]基于灰色关联的思想,以先整体后局部的次序分两级关联修正灰色关联矩阵,并利用灰色关联度最大值方法实现关联。文献[12]针对分叉轨迹、交叉轨迹和组合轨迹在关联中正确率不高的问题,基于加权思想获取关联质量,引入信息散度构造加权关联图进行关联。文献[13]基于模糊理论,选取部分关联影响因素进行加权处理,计算得到综合模糊隶属度曲线,利用双门限检测确定关联对实现关联。但文献[8-13]算法均需以时间配准为前提,导致航迹数据的误差累加,影响航迹关联算法的性能。文献[14]把不等长实数序列转换为等长区间数序列,再运用灰关联模型和最大关联准则进行关联,算法无需时域配准,但航迹点被区间数取代,引入了一定的误差,影响关联的正确率。
针对上述问题,本文提出一种基于近邻平均距离的航迹关联算法,定义一种新的序列距离度量,通过计算航迹序列与单一航迹点相距最近的个平均距离作为航迹序列与单一航迹点的距离,进而得到不等长航迹序列之间的灰色关联度,利用多维分配实现航迹关联。该方法无需时域配准,可对异步不等长航迹序列进行直接关联,并且很大程度保证了航迹信息的原始性与完整性,可显著提高正确关联率。
1 序列相似度度量
坐标序列与坐标点间的近邻平均距离
设非空坐标序列={(1),(2),…,()},其中坐标点()=((),(),())∈,=1,2,…,,若对任意坐标点=(,,)∈,有距离
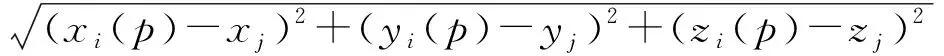
设≤≤…≤≤…≤按非减次序排列,则称
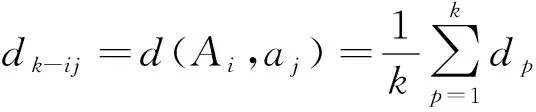
(1)
为坐标序列与坐标点间的近邻平均距离。
不等长坐标序列间的相似度
设坐标序列集合={,,…,,…,}和坐标序列={(1),(2),…,()},其中坐标点()=((),(),())∈,且序列与长度不等,则坐标序列与坐标序列的相似度定义为
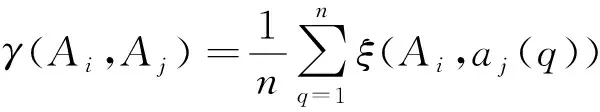
(2)
式中:
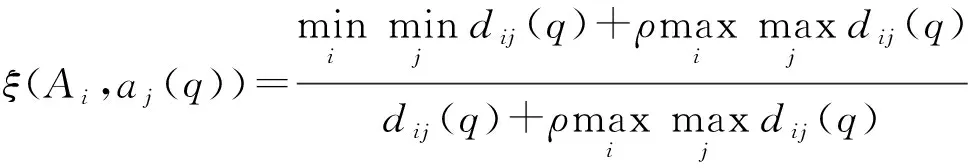
(3)
表示坐标序列与坐标序列的灰关联系数。其中,=1,2,…,;=1,2,…,;实数∈[0,1]表示分辨系数;()=-()=(,())。
定义1与定义2中坐标变量均为三维坐标,因此适用于三维空间;若定义1与定义2中坐标变量用二维坐标表示,则可适用于二维平面。
2 基于k近邻平均距离的航迹关联算法
2.1 基本思想
假设两局部节点、对公共观测区域内的多批目标实施跟踪,输出的航迹号集合分别为
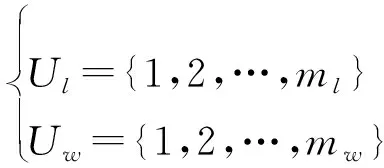
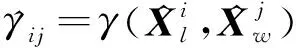
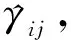
2.2 异步航迹相似度的计算
假设各局部节点异步且采样速率不同,为融合中心固定的一个时间处理周期,以融合中心第个处理周期[(-1),]为例,局部节点、跟踪上报的航迹批数分别为,,则上报的目标航迹集合()可记为
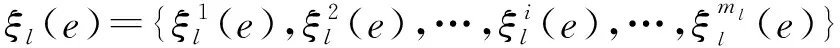

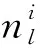
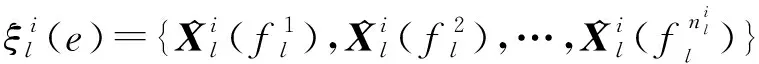
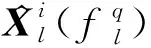
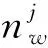
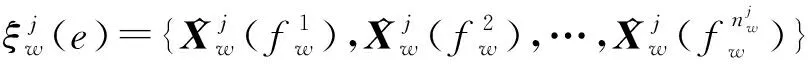
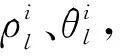
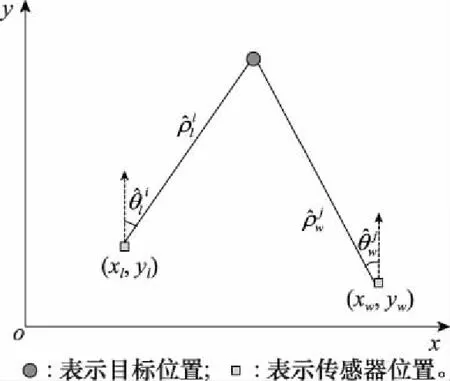
图1 局部节点对目标的测距和测角示意图Fig.1 Diagram of cocalnode ranging and angle measurement of target
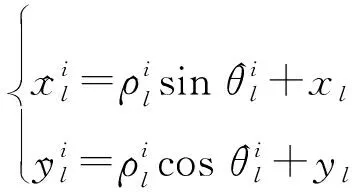
(4)
利用式(4),可将局部节点的第条航迹序列记为
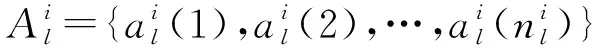
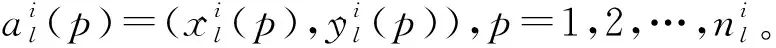
则来自局部节点的第条航迹可记为
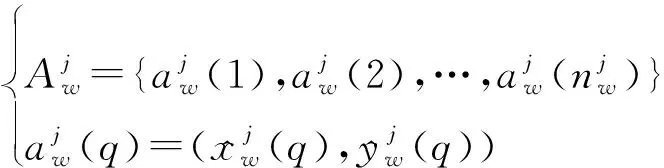
以局部节点的全部航迹作为比较序列,局部节点的第条航迹作为参考序列,利用坐标序列定义航迹点坐标关联列向量为
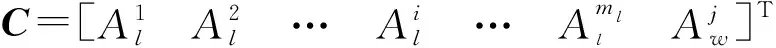
(5)
式中:前行表示比较序列的航迹数据;第+1行表示参考序列的航迹数据。
根据航迹异步不等速率的不同情况讨论的取值问题。
(1) 局部节点采样速率一致、开机时机不一致
如图2所示,可以看出,局部节点、的航迹点交叉分布,因此,可用局部节点的航迹点与局部节点航迹中对应时刻前后的临近两个航迹点的平均距离作为局部节点航迹点与局部节点航迹序列的距离,故取2时关联效果最佳。
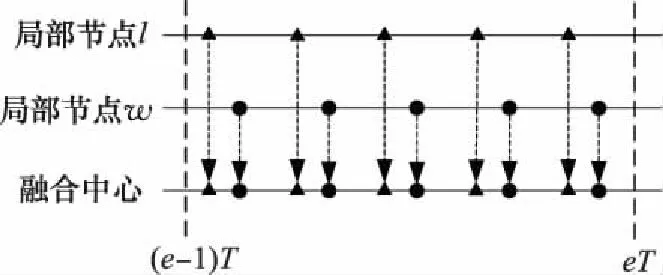
图2 局部节点时延示意图Fig.2 Diagram of local node delay
(2) 局部节点开机时机一致、采样速率不一致
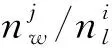
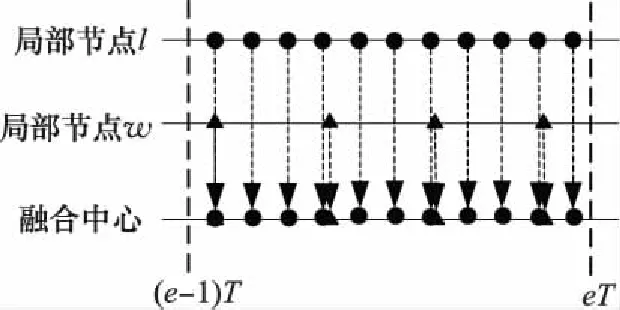
图3 不等长航迹示意图Fig.3 Diagram of unequal length track
(3) 局部节点采样速率和开机时机都不一致
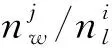
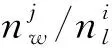

(6)
式中:INT[]表示不小于的最小整数。
根据定义1中对坐标点与坐标序列间距离的定义,计算比较序列与参考序列间的近邻平均距离矩阵为
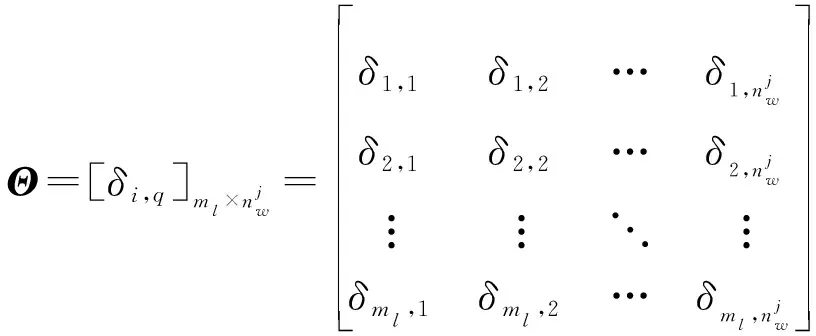
(7)
式中:
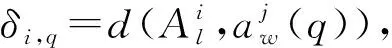
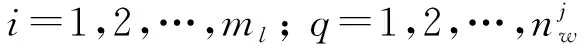
(8)
进一步利用定义2可以求得局部节点的第条航迹与局部节点的第条航迹间的灰色关联度为
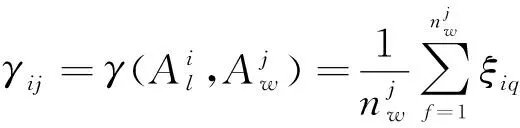
(9)
式中:
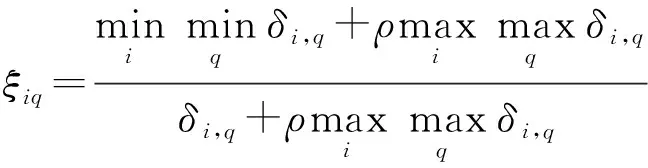
(10)
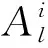
2.3 异步航迹关联判决
利用经典分配法对灰色关联度进行航迹关联判决,先分别对局部节点上报的条航迹和局部节点上报的条航迹计算灰色关联度,将其组成×维灰色关联度矩阵,通过对分配问题的求解找出全局最优航迹关联对即可。
令变量

(11)
将目标函数记为
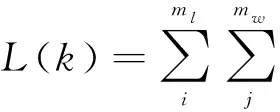
(12)
构成以下二维分配问题
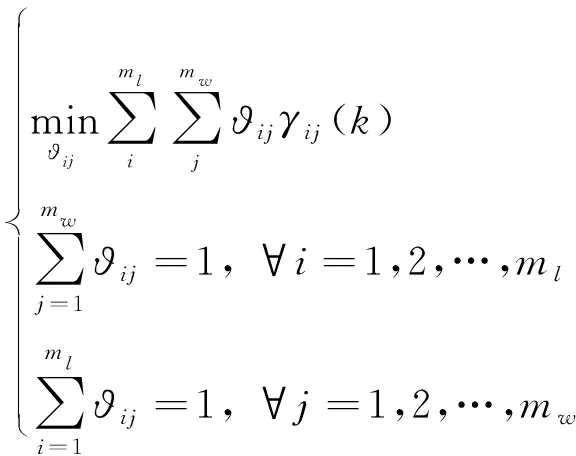
(13)
图4给出了基于近邻平均距离的异步航迹关联算法流程图。
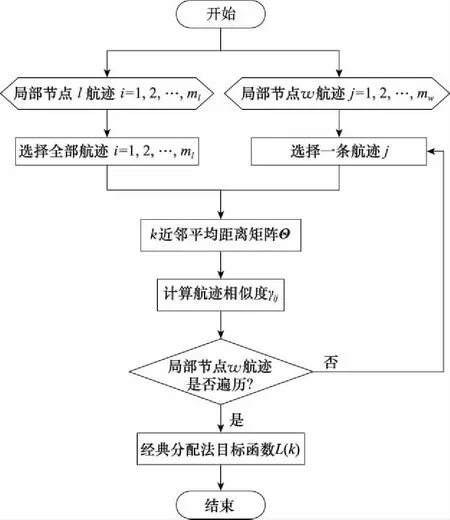
图4 异步航迹关联算法流程图Fig.4 Flow chart of asynchronous track-to-track association algorithm
3 仿真分析与验证
3.1 仿真环境
假设分布式系统中有两个2局部节点对公共区域内的20批目标持续跟踪观测35 s,若局部节点1、2异地配置,坐标分别为(0,0)km、(100,0)km,局部节点1的采样周期为=02 s,局部节点2的采样周期为=05 s,局部节点2开机时机比局部节点1延迟02 s。
假设所有观测目标都处于二维平面匀速直线运动状态,且起始运动方向和初速度随机分布在0~2π rad、200~400 m/s内。局部节点1的测距和测角误差分别为1=150 m、1=003 rad;局部节点2的测距和测角误差分别为2=180 m、2=002 rad。
采用正确关联率作为航迹关联结果的评价指标:
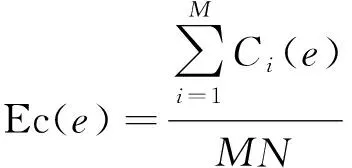
(14)
式中:()为融合中心在第个处理周期内正确关联的航迹批数;为仿真实验的蒙特卡罗次数;为局部节点观测目标航迹的总批数。
3.2 k的取值分析
对取值做出简要理论分析:如若取值为1,相当于未对异步航迹情况做出处理。
表1给出了≥2时的正确关联率和耗时对比。可以看到,随着取值由2增加到7,耗时增加明显,这是因为取值增大会导致计算量明显增加。

表1 k取值不同的耗时变化Table 1 Change in time for different values of k
表2给出了不同取值和采样周期的正确关联率。可以看到,若局部节点1、2采样周期比值小于等于1,则正确关联率在取值为2时最大;若局部节点1、2采样周期比值大于1小于等于2,则正确关联率在取值为3时最大;若局部节点1、2采样周期比值大于2,则正确关联率固定在取值为4时最大。这是由于若采样周期比值较小,则说明获得的航迹序列数目相差甚微,此时若取值过大,则与参考航迹序列点距离较远的比较航迹序列点也会参与航迹距离的计算,使关联正确率降低;若采样周期比值较大,则表示航迹序列数目相差甚多,此时若取值过小,则相当于用较少的航迹点间距离代替整条航迹间距离进行计算,易因数据不够充分而导致正确率降低。
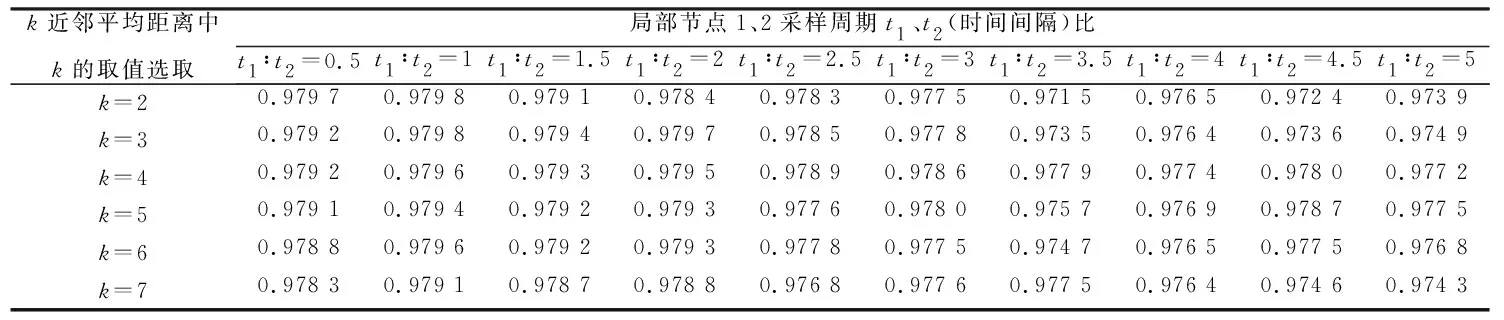
表2 不同k取值和采样周期比的正确关联率变化Table 2 Comparison of correct associating rates for different values on k and the ratio of sampling periods
3.3 算法性能比较与分析
为验证本文算法的可行性和优越性,实施120次蒙特卡罗仿真实验,改变实验条件,对不同算法之间的性能进行比较分析。
图5给出了不同算法的航迹正确关联率对比。可以看到,由于文献[16]算法中的离散度属于统计学度量,需要一定的数据量作为前提,因此正确关联率受采样时间长短的影响较大;文献[17]算法利用最小二乘法实现异步航迹同步化,估计误差传播会导致正确关联率较低;文献[14]算法由于采用虚实混合变换方法对异步航迹进行同步,没有误差传播,因此正确关联率较高,但将实数序列变换为区间数和实数的混合序列会使航迹计算精度降低;本文算法利用序列距离度量,对异步航迹直接关联,没有误差的传播和引入,因此从采样初期起就一直保持很高的正确关联率。
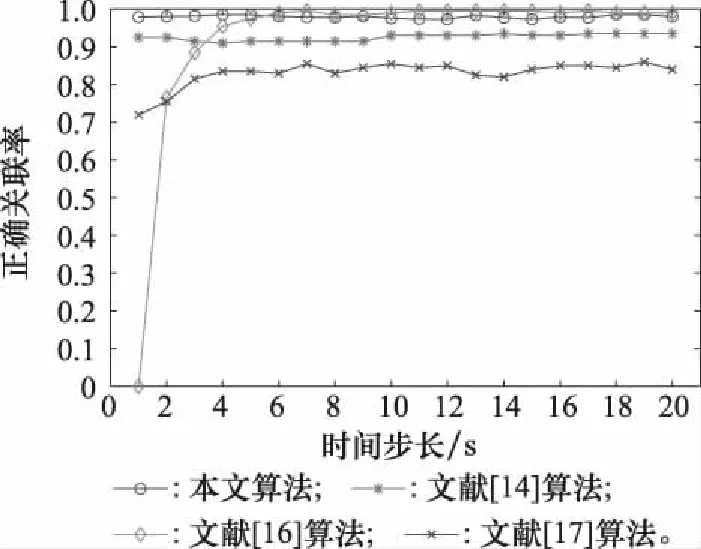
图5 不同算法的正确关联率对比Fig.5 Comparison of correct associating rates for different algorithms
图6给出了不同目标航迹数目下4种算法的耗时对比。可以看出,随着目标数目从10增加到40,各算法的耗时也在逐步增大,其中文献[14]算法耗时最长,这是由于该算法需要对航迹序列的大部分航迹实数点做区间数变换处理,过程较为繁琐;文献[16]算法耗时较高,因为算法中的离散度求取包含标准差计算,因此计算量较大;文献[17]算法作为早期经典算法,较为简单,因此耗时最短;而本文算法没有对异步航迹序列做变换处理,只需对不等长航迹序列直接计算出航迹点距离的最短平均值即可,因此耗时也较短。
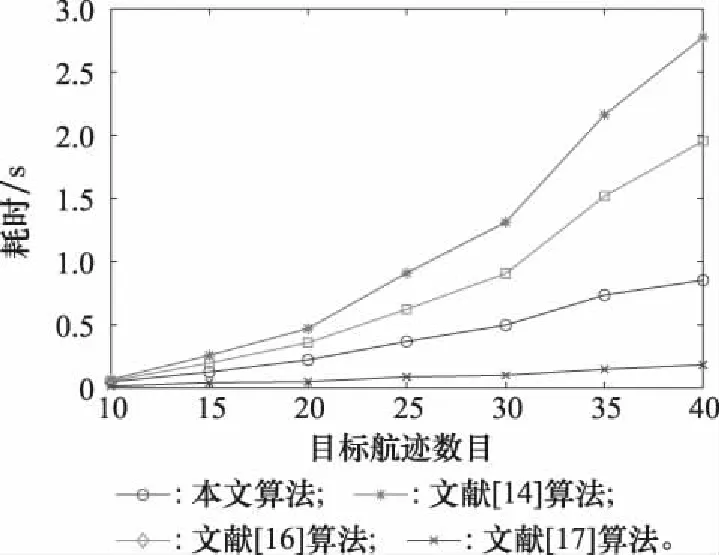
图6 不同目标航迹数目的耗时Fig.6 Time consum for different target track numbers
3.4 异步航迹关联有效性分析
图7比较了两局部节点采样率不同情况下4种算法的正确关联率。随着采样率相差越来越明显,即异步航迹序列点的数目相差变大,可以看出,文献[16]算法主要比较两条航迹的空间位置相似性,当航迹点数目不满足一定的统计学数据量时,正确关联率会有一定波动;文献[17]算法的正确关联率下降最为明显,这是因为通过最小二乘法对异步航迹序列同步化,需要对两条不等长航迹序列进行插值补齐,异步航迹点数目相差越大,需要补齐的航迹点越多,估计传播越大;而本文算法和文献[14]算法的正确关联率受其影响不大,稳定性较佳,因为两个算法都是利用距离度量来判断两条航迹的相似性,对航迹点数目差异不敏感。
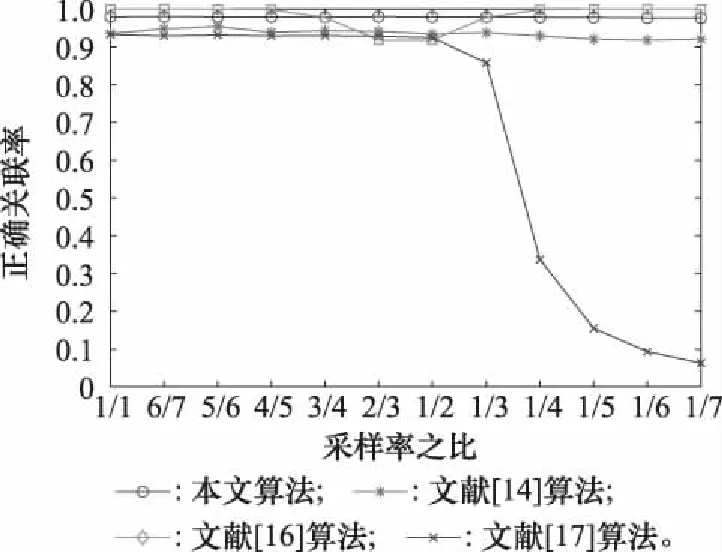
图7 正确关联率随采样率之比的变化Fig.7 Change of the correct correlation rate with the ratio of the sampling rate
由表3可知,无论是开机时间还是采样周期,对本文算法的正确关联率都无明显影响。这是因为采样周期不同只是导致航迹点数目不一致,但本文算法核心是计算单一航迹点与其他航迹序列的近邻平均距离,并不要求航迹等长;局部节点开机存在时间差异会导致上传的航迹点时间不一致,但本文算法中对航迹序列间距离的求解并未利用时间信息,所以不需要航迹点的时刻一一对应。
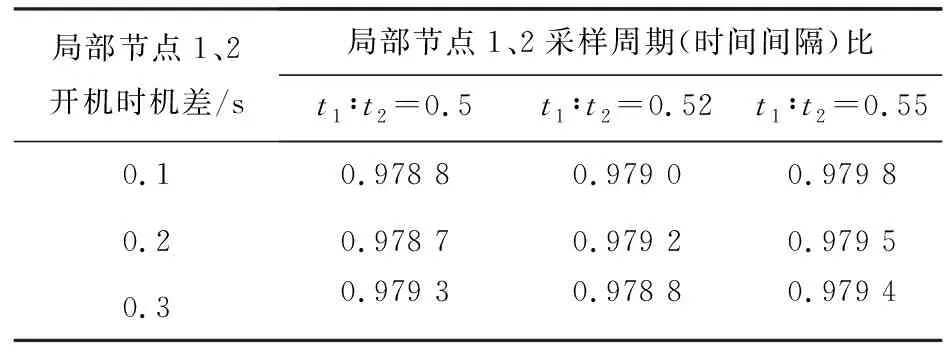
表3 不同采样周期和开机时机的正确关联率对比Table 3 Comparison of correct associating rates for different sampling periods and startup times
3.5 算法其他性能分析
改变仿真环境中目标航迹总数,目标密集程度对算法正确关联率的影响如图8所示。可以看出,在目标数目增多时,文献[14]算法的正确关联率下降最为明显,这是因为异步航迹区实变换后,区间重合度较高,以航迹全部数据点求解的传统距离容易在数值上接近,难以辨别;文献[17]算法虽然比较稳定,但正确关联率较低;文献[16]算法正确关联率较稳定,这是因为该算法基于离散度,涉及均值与方差的求解,单一数据对其影响较大,故即便航迹数目增加,只要航迹非同源,离散度对其辨别能力一直较高;本文算法仅取距离最近的个点计算近邻平均距离,可有效增加非同源航迹间距离的差异度,故正确关联率受目标数目影响较小。
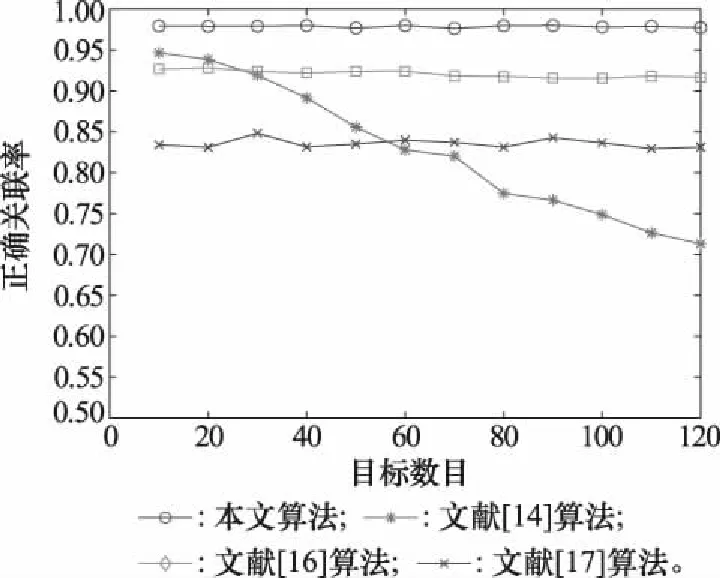
图8 不同目标数目的正确关联率Fig.8 Correct associating rates of different targets number
改变仿真环境中的噪声分布形式,算法正确关联率的变化如表4所示。由表4中数据可知,本文算法在高斯、瑞利、指数和均匀4种噪声分布形式下均能保持较高的正确关联率,基本不受噪声分布形式的影响。

表4 不同噪声分布形式的正确关联率Table 4 Correct associating rates of different noise distributions forms
4 结 论
为解决异步不等速率航迹关联问题,本文给出不等长航迹序列间的距离计算规则,用航迹序列与航迹点的距离取代传统两航迹点间距离,可对目标航迹序列直接计算距离,最大程度保证了航迹信息的完整性和原始性,避免了误差的引入,具有很高的关联正确率。
算法无需时域配准,可对异步航迹直接关联,能有效克服来自局部节点采样周期不一致和开机时间不同造成的影响,且不受目标数目密集程度影响,不受噪声分布影响,具有良好的抗噪能力。
