基于数据质量评估的自适应序贯航迹关联算法

张 瑜, 吴 凯, 郭 杰,*, 葛志闪, 张宝超

(1. 北京理工大学宇航学院, 北京 100081; 2. 上海机电工程研究所, 上海 201109)

0 引 言

航迹关联是分布式多传感器信息融合系统中的关键步骤,用于判断各传感器的局部航迹是否来自同一目标。良好的关联效果是航迹跟踪的基础,其结果将直接影响后续航迹融合精度。基于统计的方法是一类经典的航迹关联算法,主要有加权法、修正法、经典分配法、序贯关联法和双门限法等。这类方法通常实现简单、计算量小,工程应用潜力大。其中,序贯航迹关联算法(sequential track-association algorithm, STA)是对加权法和修正法的改进,在没有明显增加计算负担的前提下提高了算法在密集目标环境下的关联效果。

但在实际工程应用过程中,传感器本身存在测量误差,增大了关联难度,尤其是在传感器受到干扰、环境遮挡等因素的影响下,测量误差进一步增大,往往会出现与先验信息不匹配、不同传感器对同一目标探测数据不一致等问题,使得STA在应用时出现错、漏关联的情况,不能对传感器的局部航迹进行有效的判定。针对传感器误差存在时的航迹关联问题,文献[11-13]从观测数据中提取目标间的拓扑信息实现误差存在下的航迹关联,文献[14-16]借鉴了图像处理中的方法将航迹关联问题转化为图像配准问题。然而,上述研究认为传感器量测误差是非时变的,难以应用于真实场景下量测误差时变的情况。文献[17-21]考虑航迹评估结果,在数据预处理时进行了数据剔除、择优操作,但只是航迹融合前的预处理,没有考虑航迹质量对关联的影响,融合精度有待进一步提高。

也有部分研究者利用航迹质量对关联门限进行调整,一定程度上可以适应量测误差变化或目标机动的情况。文献[22]采用熵权法分析数据的不确定性,对最近邻域算法中的统计距离关联准则进行优化。文献[23]以量测数据与系统航迹间的误差信息及其变化率为依据,对联合数据关联算法的关联门进行调整。然而,现有方法往往是针对点迹关联问题提出的,难以应用于分布式传感器网络。且大多只从距离衡量量测数据与系统航迹间的差异,若出现传感器精度下降、不同传感器间探测数据不一致等情况,数据本身的不确定性较大,难保证根据距离差异调整门限的合理性,因此有必要设置合理的门限调整策略。

为应对传感器精度下降时的航迹关联问题,提出了一种自适应STA(adaptive STA, ASTA),以实时航迹质量评估结果为依据调整经典STA中的门限大小。采用含有历史信息的距离指标衡量局部滤波质量,进一步将传感器性能考虑在内,采用Sage-Husa估计器对传感器距离、方位角及高低角量测精度进行实时估计,利用熵值法确定各个量测分量的权重,结合效用函数法得到传感器性能评估结果;采用模糊方法构建两项指标与算法显著性水平之间的关系,进而实时调整关联门限的大小,保证传感器精度下降时的有效关联。

1 问题描述

1.1 系统方程

设线性离散系统的状态方程和量测方程分别为

()=(-1)(-1)+(-1)(-1)

(1)

()=()()+()

(2)

式中:()为系统状态向量;()为系统观测向量;(-1)是系统状态转移矩阵;(-1)为系统噪声矩阵;()为系统量测矩阵;()为系统噪声向量,服从零均值高斯分布,协方差矩阵为();()为量测噪声向量,服从零均值高斯分布,协方差矩阵为()。

三维运动下,目标状态向量为

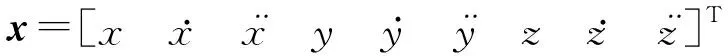
(3)

式中:、、为东北天坐标系下目标的位置分量。

雷达直接探测得到的实际量测为球坐标系下目标与探测源的距离、方位角和高低角,其观测噪声满足协方差矩阵:

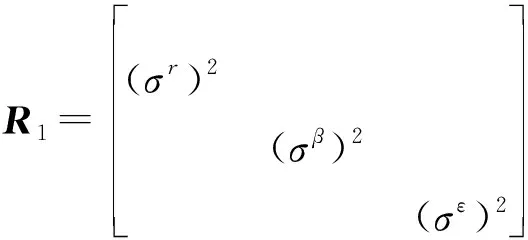
(4)

式中:,,分别为距离、方位角、高低角测量误差的标准差。

由于滤波处理在直角坐标系下进行,因此将东北天坐标系下的3个位置分量[,,]作为虚拟量测输入到滤波器中,依据几何关系即可得到实际量测与虚拟量测之间的转化关系:

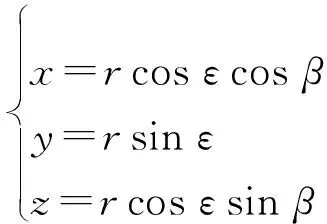
(5)

根据协方差传播理论,可以得到虚拟量[,,]的协方差矩阵与之间的转换关系:

=

(6)

式中:

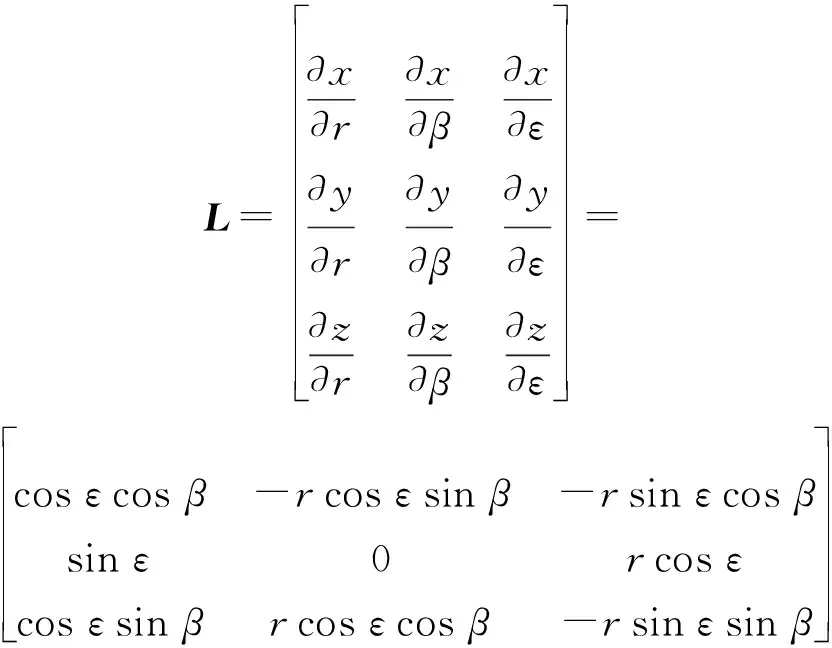
1.2 STA原理

考虑空间内存在多台雷达传感器的情况,在分布式传感器网络中,将各个节点经滤波处理过的局部航迹送入融合中心与系统航迹进行关联。

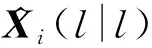
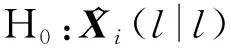
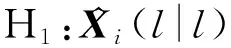
何友等借用雷达信号检测中的序贯检测思想,提出了STA。该方法把航迹当前时刻的关联与其历史联系起来,关联性能较加权法和修正法有了较大的改善,主要步骤如下。

设时刻传感器节点处的局部滤波信息与目标的预测航迹之差为

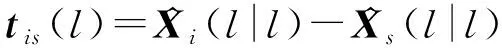
(7)

假设在H的条件下时刻的估计误差()服从高斯分布,将其方差表示为(|),即()～N(0,(|)),同时假设状态估计误差独立,可以得到:

(|)=D(()())=(|)+(|)

(8)

至时刻序贯航迹关联使用的统计量为

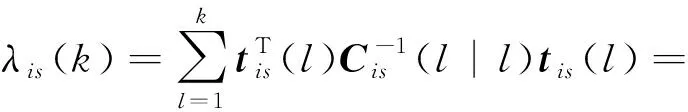
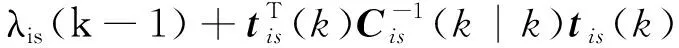
(9)

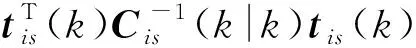
计算传感器局部航迹与当前时刻每一条系统航迹的关联统计量,选取()=min{()|=1,2,…,},然后对H和H进行假设检验,将传感器对应的关联门限表示为(),即:如果

()≤()

(10)

则接受H,否则接受H。其中,阈值满足:

(()>()|H)=()

(11)

式中:()为时刻假设检验时传感器的显著水平。在经典的STA中,()为常值,通常取005、001或01等,当传感器精度下降时,常值门限不足以适应探测环境的变化,需进行进一步调整。

2 ASTA

为对STA中的门限大小进行有效设定,选取数据质量评估指标,并构建指标与算法显著性水平之间的模糊关系,将实时数据质量引入关联门限的调整,使得算法可以适应变化的探测环境,提高关联正确率。

2.1 实时数据质量度量

传统的航迹质量评估指标主要以精确度为主,常用的指标有位置均方根误差、速度均方根误差等。但上述评估指标主要用于离线的算法效果和参数设置评估,计算需要获取目标真实信息,不能应用于在线航迹质量评估。

为了对算法参数进行实时调整,需要构建不依赖于目标真实状态的指标,从数据处理步骤以及影响关联效果的因素出发,一方面,数据质量受传感器探测精度的影响,若在传感器探测精度较低时将门限设为较小值,不能对偏差较大的数据进行有效关联,若在传感器精度较高时将门限设为较大值,则会增大引入干扰的可能性;另一方面,数据质量也受滤波的影响,滤波参数或模型选择会影响滤波质量,门限设置若不考虑滤波质量,关联效果难以提升。因此,需根据传感器性能及局部滤波质量合理调整关联门限大小。

211 传感器性能指标

(1) 传感器性能估计

实际情况下,量测误差具有实时变化、不确定的特点,Sage-Husa估计器可以对量测噪声误差方差的实时估计,给出当前探测环境的参考信息,将量测噪声的估计结果作为传感器性能评估指标引入关联门限的调整。

Sage-Husa估计器是基于极大后验的最优估计器。针对原始算法中滤波易发散的缺点,文献[27]对其进行改进提出了Sage-Husa次优无偏极大后验估计器。对于第个传感器,采用改进Sage-Husa估计器对虚拟量测误差协方差进行估计,并将估计结果引入卡尔曼滤波,其表达式为

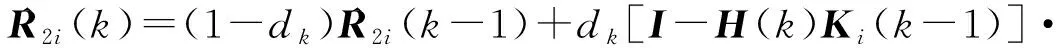
(12)

式中:=(1-)(1-+1),0<<1,为遗忘因子,其选取需在跟踪性能与对噪声的敏感性之间权衡考虑。

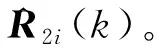
(2) 效用函数法确定效用值

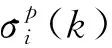
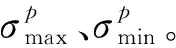
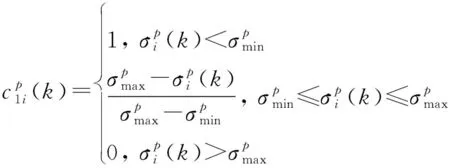
(13)

式中:=1,2,…,；=,,。

(3) 熵值法确定权重

在实际滤波过程中,Sage-Husa估计器对不同分量估计的敏感度会由于目标与探测源的相对位置和目标运动形式的不同有所差异。采用熵值法对各个量测指标进行赋权,即某个量测量的熵值越小,则该指标的离散程度越大,该指标所含的信息量越大,则对传感器性能的综合评价结果影响越大。熵值法确定权重的过程如下。

至时刻传感器的量测精度估计结果组成矩阵为

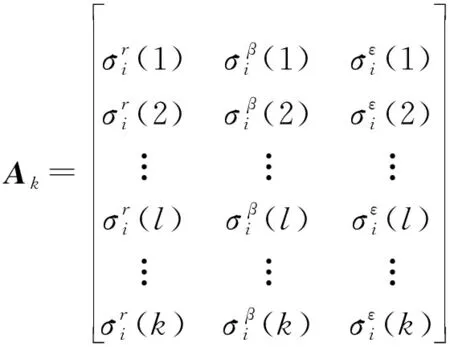
(14)

计算传感器在第项量测估计值下第个时刻所占的比重:

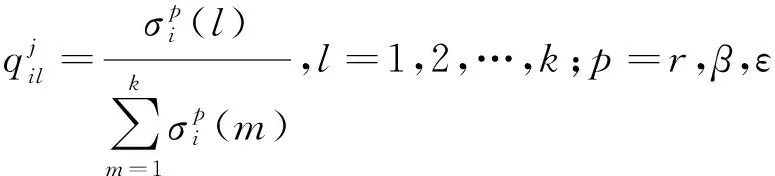
(15)

则时刻量测的熵值为

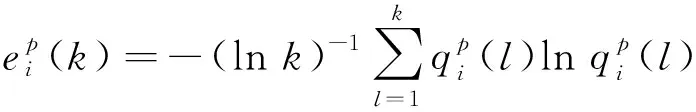
(16)

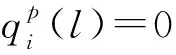
某项指标的信息效用价值的定义为1与熵值之间的差值,效用价值直接影响权重大小,信息效用值越大,对评价的重要性越大,权重越大。时刻量测量的信息效用价值为

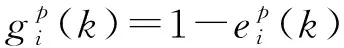
(17)

利用信息效用价值计算各个指标的权重,时刻传感器第项量测的权重为

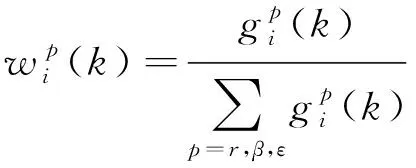
(18)

采用加权求和的方式得到时刻下传感器性能的评估结果:

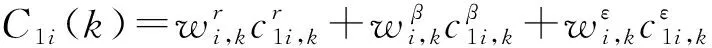
(19)

212 局部航迹质量

利用滤波中新息的协方差信息对局部航迹质量进行评估,对于第个传感器,时刻的新息为

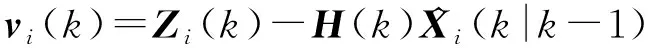
(20)

其协方差为

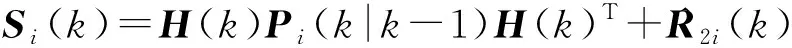
(21)

采用标准化距离衡量局部航迹质量,表示为

()=()()()

(22)

将历史航迹质量考虑在内,则时刻传感器的局部航迹质量指标为

()=(-1)+(1-)()

(23)

式中:为历史权因子,取值范围为0～1。

与传感器性能类似,局部航迹质量指标也为成本型指标,设有效值上下限分别为、,由于局部航迹质量仅有一项指标,由效用函数可直接得到评估结果,其表达式为

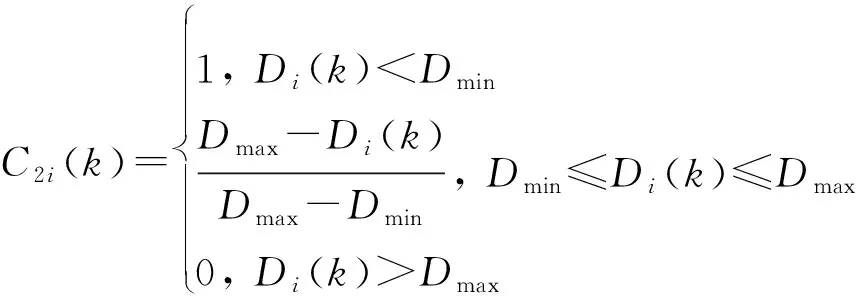
(24)

式中：=1,2,…,。

2.2 模糊关系建立

航迹关联结果受传感器量测精度、局部航迹质量影响,根据数据质量评估结果自适应调节算法参数。但由于传感器性能与局部航迹质量之间存在耦合关系,采用传统的层次分析法分级构建指标体系并进行综合评估是不合理的,违反了构建指标体系构建原则。因此,采用模糊控制器建立以上两项指标与算法显著性水平之间的模糊关系。

时刻时,将传感器的数据质量评估结果1()和2()作为模糊控制器输入量,将检验的显著水平()作为输出量,隶属度函数设置如图1～图3所示。其中,将PS、PMS、PM、PMB和PB用来分别表示小、较小、中、较大和大。

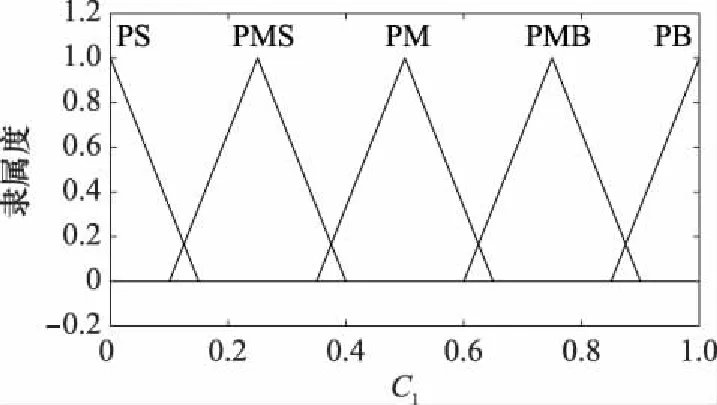
图1 C1隶属度函数Fig.1 C1 affiliation function

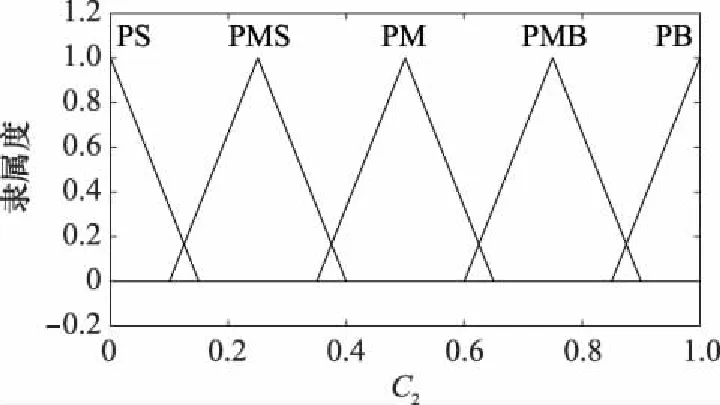
图2 C2隶属度函数Fig.2 C2 affiliation function

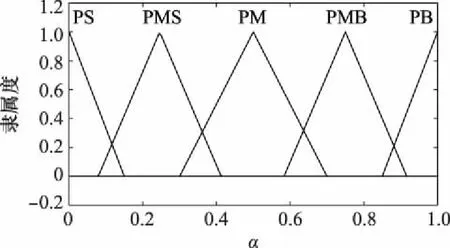
图3 α隶属度函数Fig.3 αaffiliation function

对于传感器性能指标,测量误差越小,传感器性能越好,数据的不确定性越小,应当将门限设置为较小值以减少其他因素的干扰;反之,若传感器的测量误差较大,传感器性能较差,数据的不确定性较大,此时应当将门限设置为较大值以降低漏关联的可能;而局部航迹质量是后续多源信息关联与融合的基础,若局部航迹质量较差,则可能无法对航迹对进行成功关联,在这种情况下,将门限放宽减小漏关联概率;反之当局部航迹质量较好时,则应将门限设置为较小的值以防止错关联发生。

综合上述分析,模糊逻辑设置为:传感器性能指标越大、局部航迹质量指标越大,显著性水平取值越小;反之,传感器性能指标越小、局部航迹质量指标越小,显著性水平取值越大。模糊控制器规则如表1所示,模糊控制面如图4所示。

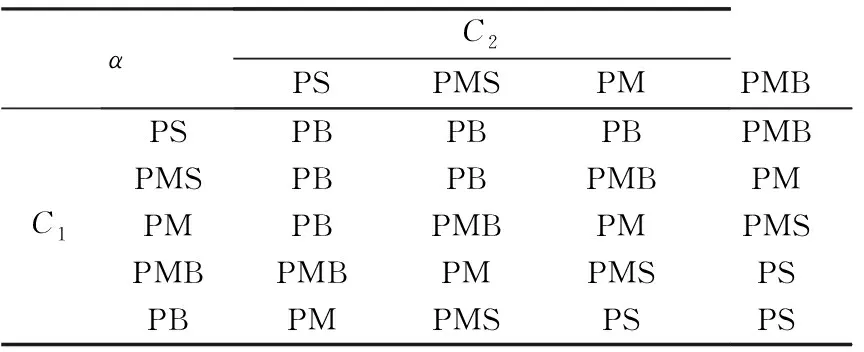
表1 模糊控制器规则Table 1 Rule of fuzzy controller

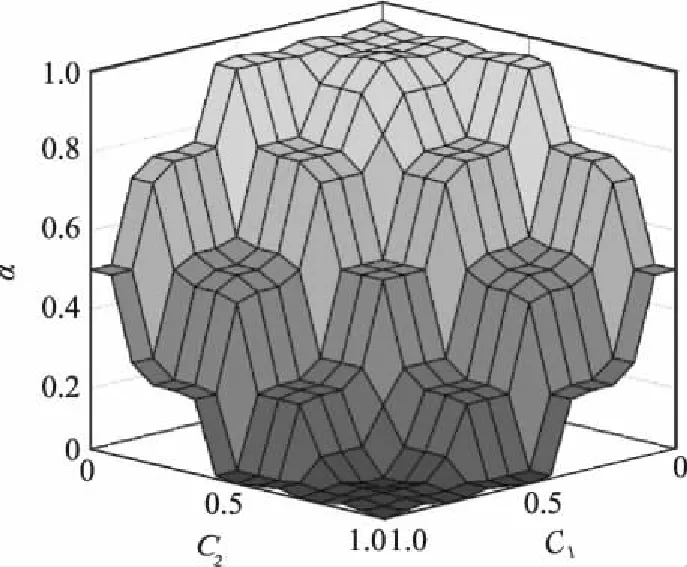
图4 显著性水平的模糊控制面Fig.4 Fuzzy control surface for significance level

根据表1和图4所示的模糊规则,由时刻传感器的性能评估值1()以及局部滤波航迹质量评估值2()可以自适应调整显著性水平()的取值,再由式(11)即可计算得到该时刻的门限值,实现关联门限的动态调整。

3 仿真分析

3.1 仿真场景

为验证本文算法的有效性,在雷达受到干扰的情况下对算法进行仿真实验,假定传感器的观测数据已经完成时空配准环节,比较本文改进的ASTA、传统STA以及文献[30]中序贯灰色关联算法(用Grey算法表示)的性能。ASTA中,设置指标有效上下限值如表2所示;STA中,设置显著性水平=0.05。完成关联处理后,均采用交叉协方差加权融合算法进行航迹融合。

表2 有效上下限取值Table 2 Upper and lower bounds of effectiveness value

滤波模型设置为Singer模型,其状态转移矩阵及系统噪声矩阵分别为

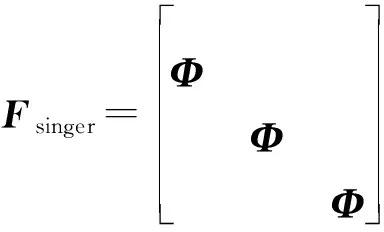
其中，

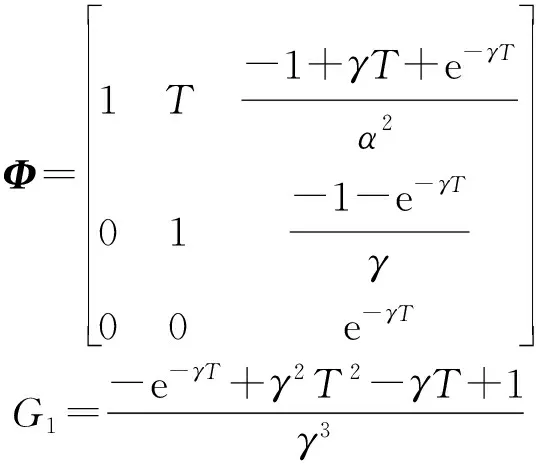
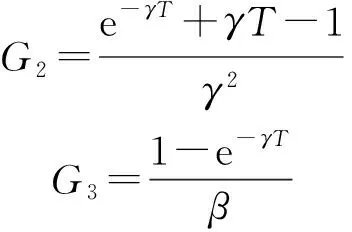
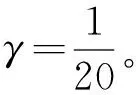
考虑对单个空中目标进行跟踪,设置匀加速直线运动和正弦机动两种运动形式,目标真实运动轨迹分别如图5和图6所示,目标机动的加速度形式见下式,相关参数如表3所示。

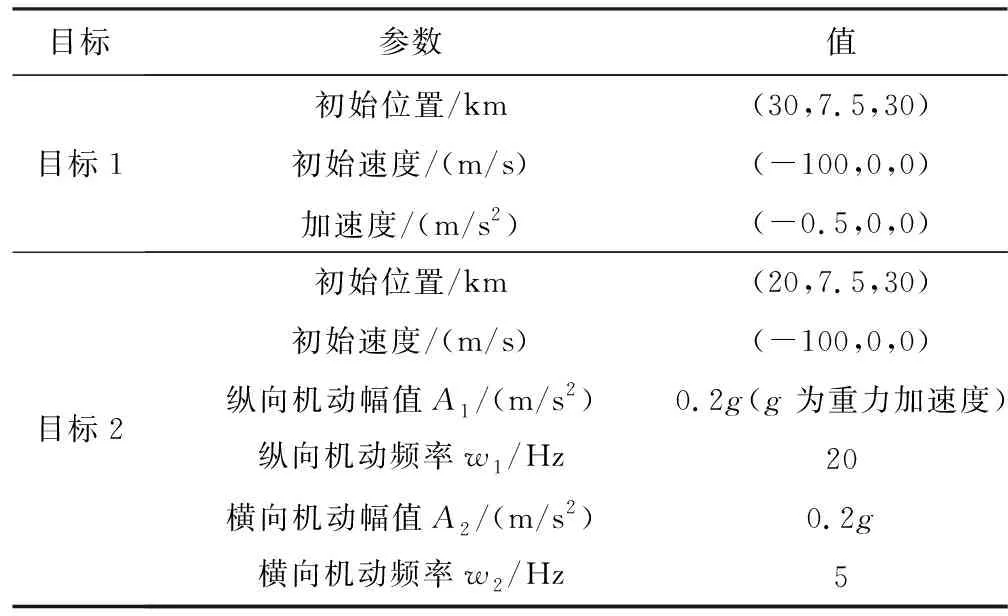
表3 目标参数设置Table 3 Set of target parameters

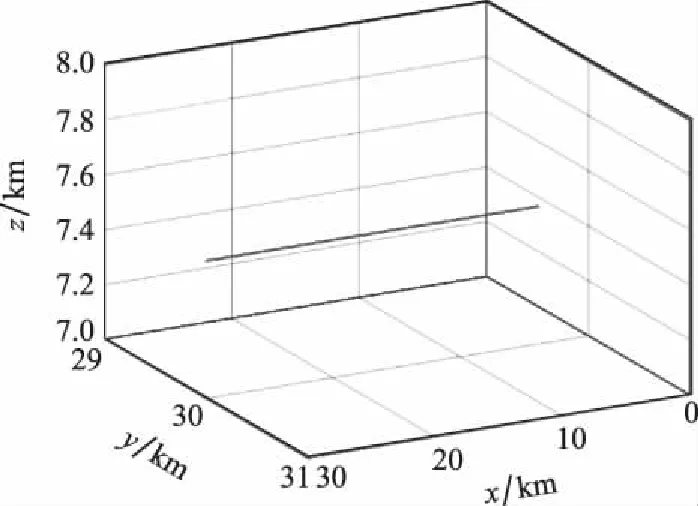
图5 匀加速运动目标Fig.5 Uniformly accelerated motion target

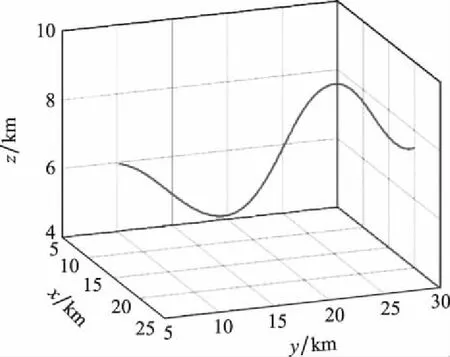
图6 正弦机动目标Fig.6 Sine maneuver target

=cos()，=1,2

(25)

采用两台雷达设备对目标进行探测跟踪,观测时长为180 s,采样周期和融合周期均为1 s,雷达的位置分别为(-10,10,0)km、(0,0,0)km,量测噪声服从高斯分布。假定雷达1在15～45 s时受到干扰,量测精度下降,两台雷达设备的量测精度设置如表4所示。

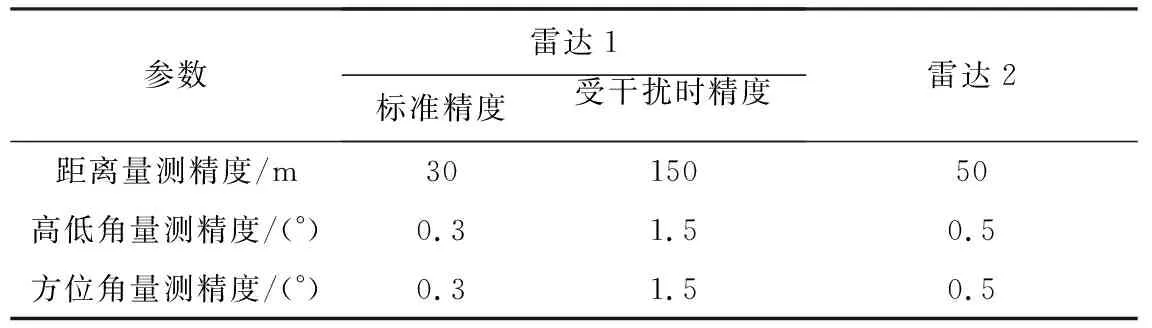
表4 传感器参数设置Table 4 Set of sensor parameters

选取关联正确率作为衡量关联算法性能的指标,对比距离、方位角和高低角均方根误差(root mean squared error, RMSE)，进一步比较关联性能对融合结果的影响。

3.2 仿真对比

3.2.1 仿真场景1

对于匀加速直线运动的目标,采用3种算法分别进行航迹关联,进一步进行融合处理,融合后航迹如图7所示,关联正确率如图8所示,两项数据质量评估结果及参数自适应结果如图9所示。可知,传感器在15～45 s内受到干扰,量测精度下降,此时STA无法对不同传感器的局部航迹信息与系统航迹进行有效关联,在航迹中段将两个雷达对同一目标的局部滤波结果误判为两个目标,且由于STA采用的检验量为历史信息的累计结果,在干扰消失后的一段时间内也不能实现局部航迹的有效关联,关联正确率持续下降。相较而言,Grey算法的正确关联率有所提升,但在15 s、47 s和132 s处出现了航迹中断的现象,不利于对当前目标态势做出准确判断。ASTA的关联效果优于Grey算法和STA,可以实时对数据质量进行评估,在雷达1的数据质量较差时相应地增大假设检验的显著性水平,能较好地实现航迹的有效关联,得到相对稳定、连续的目标航迹。

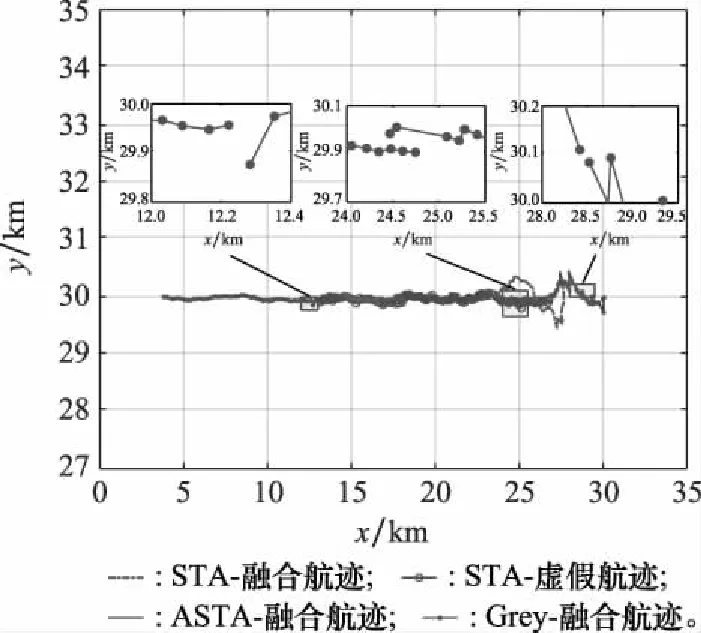
图7 场景1融合航迹Fig.7 Fusion track of case 1

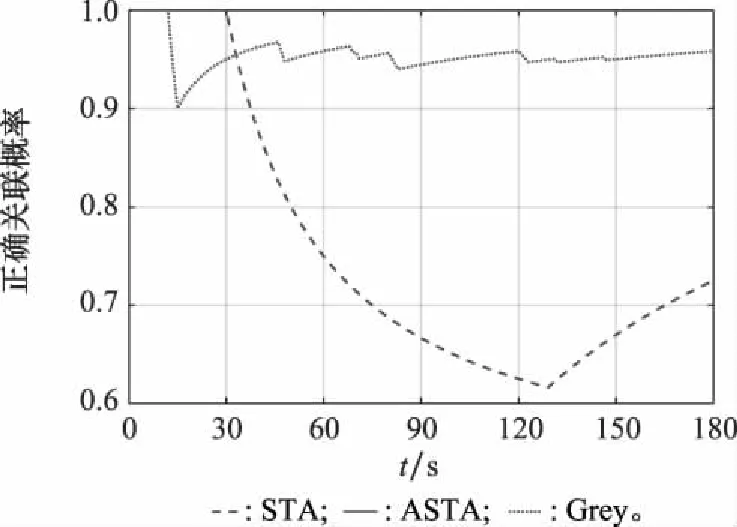
图8 场景1关联正确率Fig.8 Association accuracy of case 1

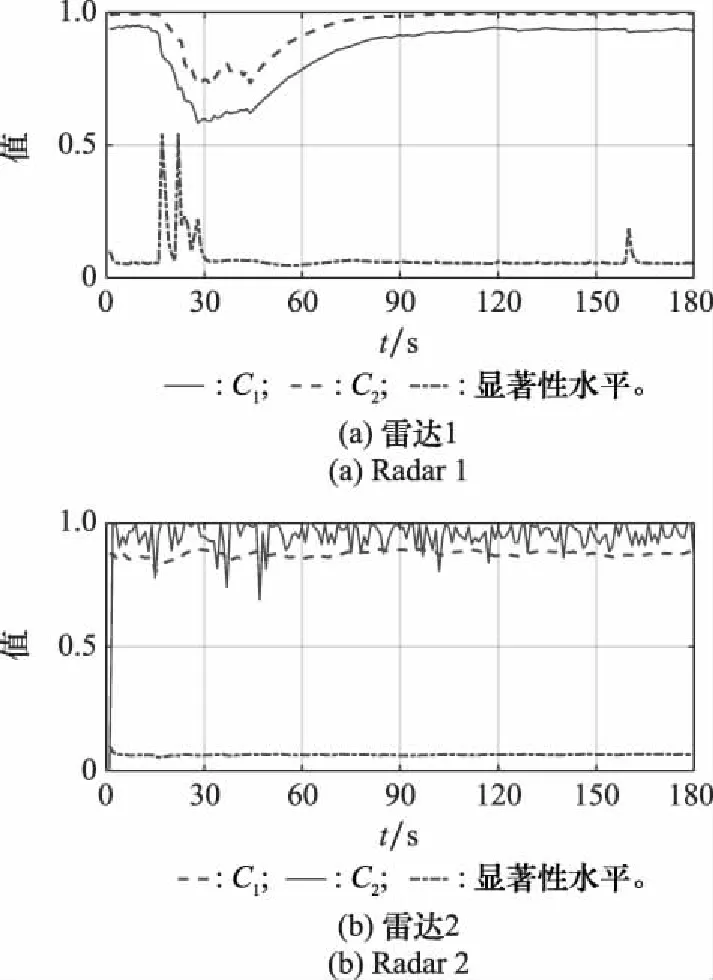
图9 场景1数据质量评估结果及参数自适应曲线Fig.9 Data quality assessment results and parameter adaption curves of case 1

在完成对目标局部航迹的关联后,进一步地采用交叉协方差加权融合算法进行航迹融合,融合后距离、高低角和方位角误差曲线如图10所示,统计RMSE结果如表5所示。对比可知,在受干扰时间段内,STA的距离、方位角、高低角误差及误差波动均明显增大,采用ASTA和Grey算法关联得到的航迹精度有明显的提升,ASTA的效果在总体上又优于Grey算法。对比统计结果,ASTA的距离RMSE、方位角RMSE、高低角RMSE相较于STA分别提升了33.93%、38.50%和41.73%,可见准确的关联结果有助于融合精度的提升。

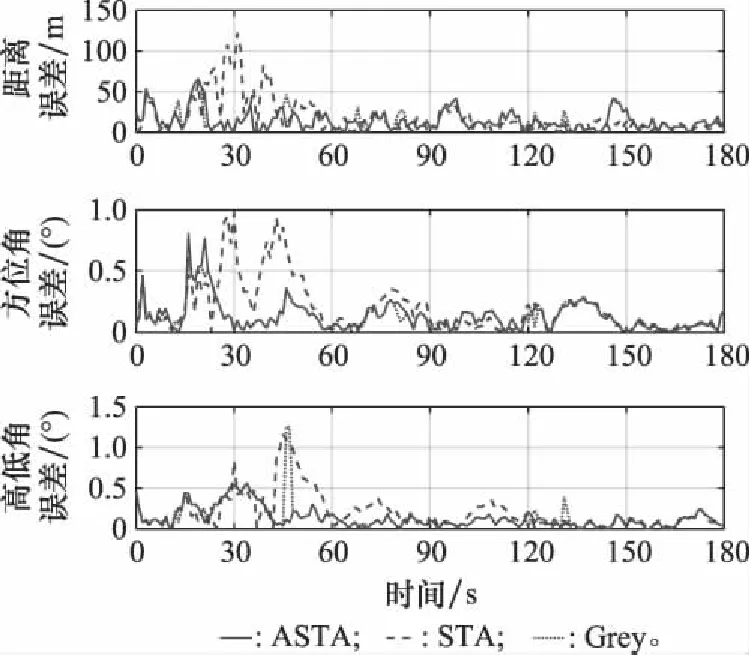
图10 场景1误差曲线Fig.10 Error curves of case 1

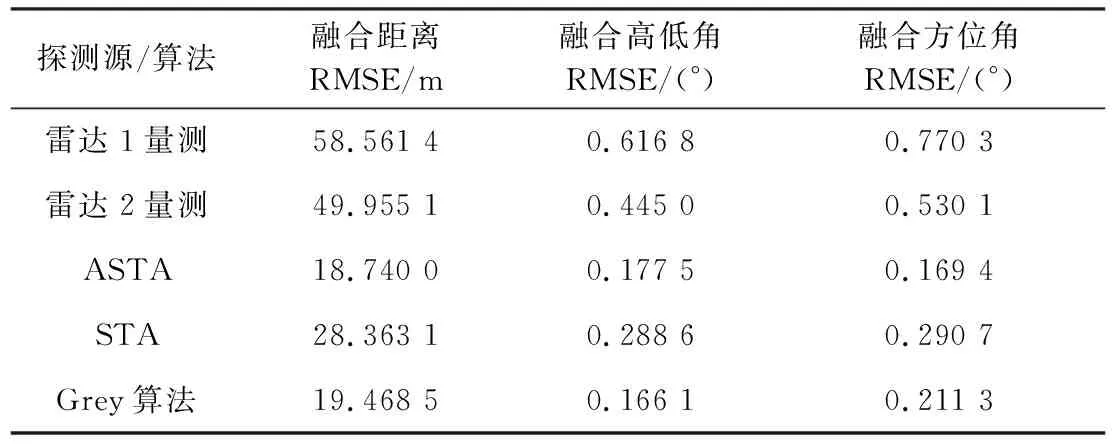
表5 场景1融合精度统计结果Table 5 Statistical results of fusion accuracy of case 1

3.2.2 仿真场景2

对于作近似正弦机动的目标,同样采用3种方法对雷达量测数据进行滤波、关联和融合处理,融合后航迹如图11所示,正确关联概率如图12所示,两项数据质量评估结果及参数自适应结果如图13所示。与场景1情形类似,STA无法对局部航迹进行有效关联,且由于初期滤波误差较大,在航迹起始及航迹中段航迹分裂为多个目标;采用Grey算法的关联结果有所改善,但在10 s、37 s、45 s、58 s、76 s、107 s及146 s处均出现了航迹中断现象。图11中展示了107s处航迹中断的局部放大情况;ASTA的航迹关联结果优于STA和Grey算法,但由于目标机动运动的存在,滤波数据质量评估结果波动较大,量测精度估计结果也不能完全与实际情况匹配,影响了算法关联性能,出现了数据点漏关联的现象。

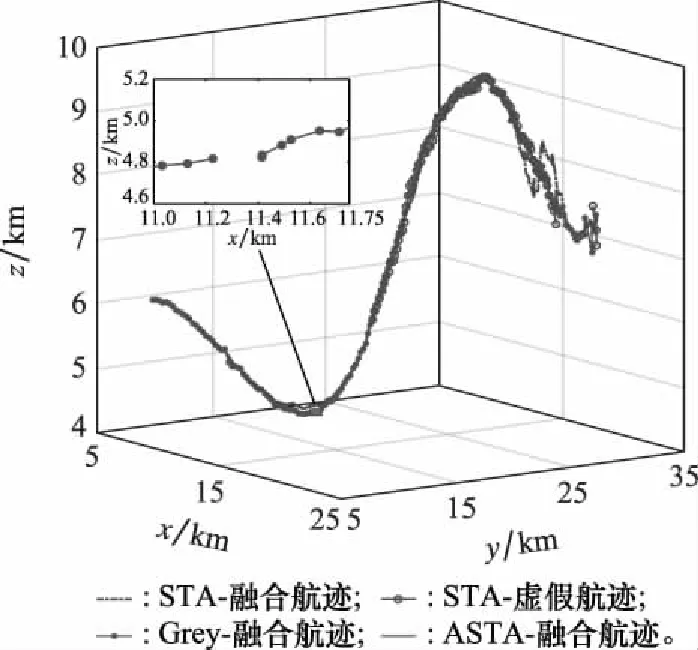
图11 场景2融合航迹Fig.11 Fusion track of case 2

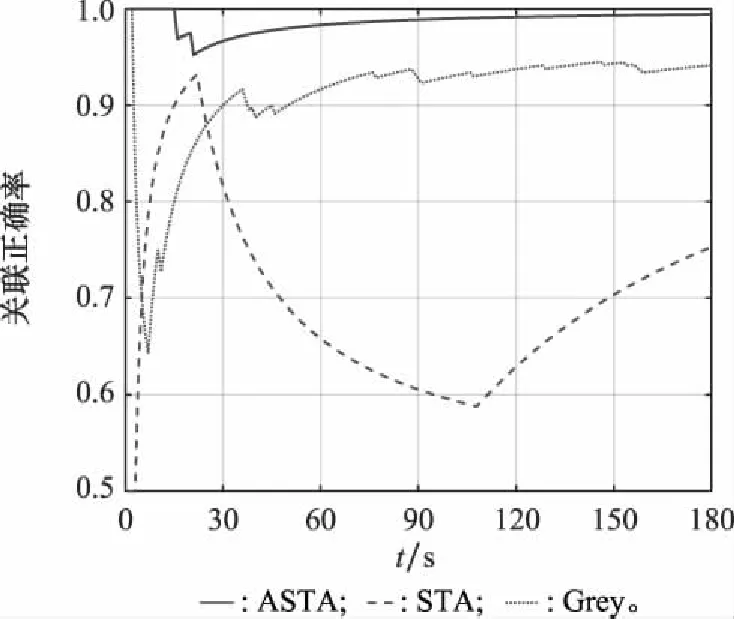
图12 场景2关联正确率Fig.12 Association accuracy of case 2

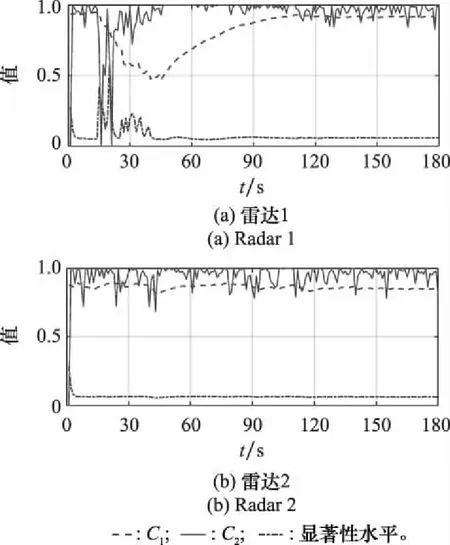
图13 场景2数据质量评估及参数自适应曲线Fig.13 Data quality assessment and parameter adaption curves of case 2

融合得到的距离、高低角和方位角误差曲线如图14所示,统计结果如表6所示。采用ASTA关联得到的航迹相比Grey算法和STA具有更高的精度,距离RMSE、方位角RMSE、高低角RMSE相较于STA分别提升了30.32%、28.68%和28.70%,这说明改进的ASTA对于机动目标的关联与融合也具有一定的效果。

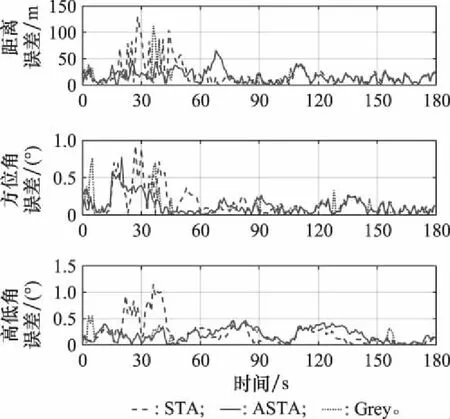
图14 场景2误差曲线Fig.14 Error curves of case 2

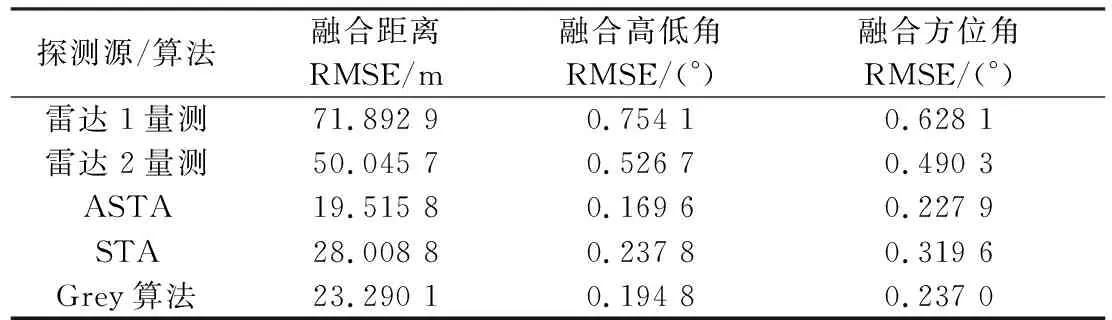
表6 场景2融合精度统计结果Table 6 Statistical results of fusion accuracy of case 2

但在噪声干扰消失后,ASTA出现了局部误差增大的情况,对比如图15所示的量测精度估计结果可知,采用Sage-Husa方法对量测噪声的估计是一个逐渐收敛的过程,在噪声干扰消失后的一段时间内并不能实时与实际量测精度匹配,因此在这段时间内融合误差易出现尖点。在120～140 s之间,改进的ASTA高低角融合误差也出现了较大的情况,这是由于目标在高低角方向上有较大的机动,对量测噪声估计结果产生影响,进而导致目标状态估计不准确。

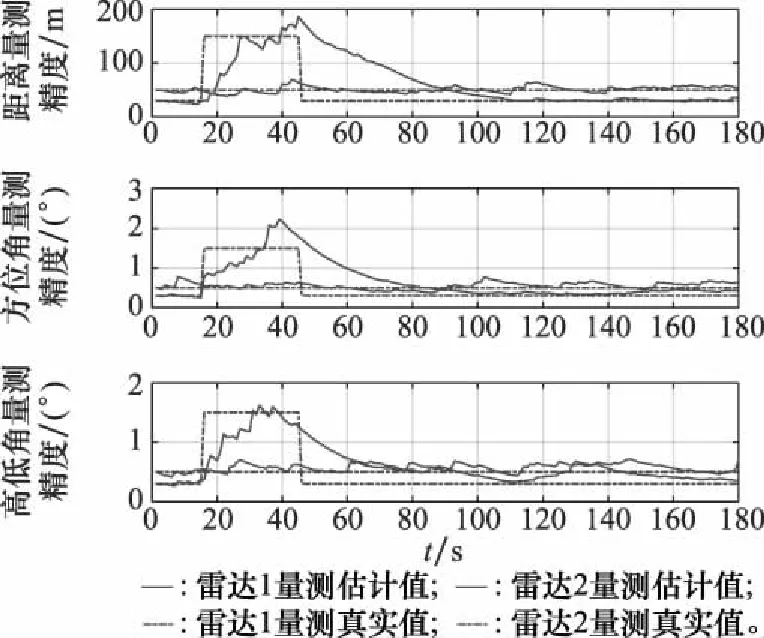
图15 场景2量测精度估计结果Fig.15 Measurement accuracy estimation results of case 2

4 结 论

(1) 为提高传统航迹关联算法在工程应用时的关联正确率,进一步提高融合精度,实时地将数据质量评估结果引入关联算法,实现关联门限的自适应调整,将实际探测环境的动态变化考虑在内,改善了关联效果。

(2) 在传感器受干扰的场景下,改进的ASTA对于匀加速运动目标能实现较好的关联效果,相比于STA,距离、高低角和方位角融合精度分别提升了33.93%、38.50%和41.73%;对于近似正弦机动的目标也具有较好的适应性,距离、高低角和方位角融合精度相较于STA分别提升了30.32%、28.68%和28.70%。

为进一步提高航迹关联算法在实际问题中的关联性能,可将探测数据不连续、起伏大、传感器异构等情形综合考虑在内。