基于改进得分函数和前景理论的区间值毕达哥拉斯模糊多属性决策

尹东亮, 崔国恒, 黄晓颖, 张 欢

(海军工程大学作战运筹与规划系, 湖北 武汉 430033)

0 引 言

多属性决策作为一种常用的决策方法,由于决策人知识水平等方面的局限和事物本身的模糊性,往往难以用精确值对事物进行评价。针对这一问题,1965年Zadeh首次提出模糊集以对信息的不确定性进行刻画。Atanassov在其基础上扩展,提出了包含隶属度、非隶属度和犹豫度的直觉模糊集(intuitive fuzzy sets, IFS),三者总和为1。但当隶属度、非隶属度分别由决策人独立给出时,由于决策本身的模糊性和事物刻画的细致程度不同,可能就会存在其总和大于1的情况。因此,Yager等提出毕达哥拉斯模糊集(Pythagorean fuzzy set, PFS),隶属度、非隶属度的平方和不大于1,拓展了其空间范围。而随着决策复杂性和不确定性不断提高,决策人可能难以用一个具体值准确给出隶属度或非隶属度。

针对该情况,结合区间数的相关知识,区间值毕达哥拉斯模糊集(interval-valued Pythagorean fuzzy set, IVPFS)的概念被提出,可用区间的形式表示隶属度或非隶属度。在多属性决策领域,文献[9]基于IVPFS对产品设计要求和客户需求进行衡量和排序,结合质量功能展开 (quality function deployment，QFD)在太阳能光伏发电发展应用过程中开展评估决策;文献[10]针对共享电动自行车回收供应商选择问题,定义了区间值毕达哥拉斯模糊偏好关系(interval-valued Pythagorean fuzzy preference relation, IVPFPR)的概念,提出一种考虑信任程度的毕达哥拉斯模糊决策方法;文献[11]针对如何有效分析和提取网络评论中相关意见,引入IVPFS来表示区间值,提出了一种结合特征-意见IVPFS的产品排序方法;文献[12-14]利用IVPFS中隶属度、非隶属度的相关测度,分别对无人驾驶汽车风险评估、可持续供应商选择以及高技术项目组合评价等问题开展了决策分析和研究。

以往研究中,一般都假设决策人是完全理性的,未考虑其偏好习惯等因素对决策的影响;同时区间值之间难以精确比较,给决策带来不便。前景理论针对决策人面对风险时“有限理性”的心理状态,以前景价值函数的形式来体现决策人由于损益表现出的主观感受价值,在多属性决策中应用广泛;得分函数可以将区间数转化为精确单一数值,便于对比决策。文献[20]针对PFS现有得分函数的不足,定义了一种新得分函数,提出了基于新得分函数和累积前景理论的毕达哥拉斯模糊熵权逼近理想解排序法(technique for order preference by similarity to ideal solution, TOPSIS);文献[21-22]针对IVPFS环境,利用得分函数进行排序优选开展了多属性决策工作。

从相关研究可以看出,得分函数虽然便于对比,但并未考虑犹豫度对决策的影响,一般决策人希望最优决策的犹豫度越小越好,同时犹豫度往往会偏向于受支持程度较大的方案,这都会对决策结果产生一定的影响。

综上,本文针对得分函数未体现犹豫度的问题,提出了改进后的新得分函数,涵盖犹豫度对决策的两方面影响,并证明了其相关定理和性质,同时引入前景理论描述决策人的主观感受对决策的影响,在区间值毕达哥拉斯模糊环境下,基于TOPSIS法,假设决策属性的权重已知,利用前景价值函数得出正负理想方案的新得分函数值,对不同备选方案和理想方案的得分函数贴近度进行分析,得出各方案的综合损益值和损益比,对损益比进行排序,确定最优决策结论。最后,利用算例对本文改进方法进行正确性和有效性验证,并与以往其他方法对比分析,证明该方法的优越性。

1 相关基础知识

设为一个论域,则该论域中的一个PFS可表示为

={〈,(),()〉|∈}

(1)

一个PFS的某一元素((),())称为毕达哥拉斯模糊数(Pythagorean fuzzy numbers, PFN),也可表示为=(,)。

(2)

1979年,Kahneman和Tversky提出了前景理论,定义前景价值由价值函数和概率权重函数确定。1992年,两人又提出价值函数的定义如下:

16令表示某一参考点,数偏离的大小为Δ,则Δ≥0表示相对于获得收益,Δ≤0表示相对于有所损失,设置的价值函数为

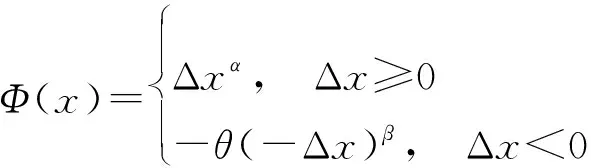
(3)

式中:>0,表示决策人对收益的敏感度;<1,表示决策人对损失的敏感度;>1,表示相对于收益,一般对损失更敏感。

2 区间值毕达哥拉斯模糊得分函数

2.1 现有得分函数分析

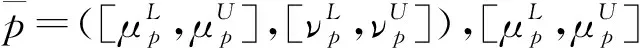
(4)

由于该得分函数在某些情况下难以区分IVPFN的大小,Zhang提出了精确函数的定义：

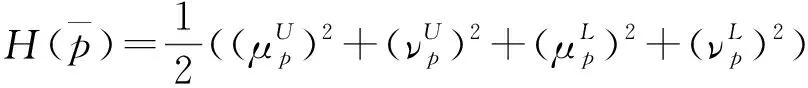
(5)

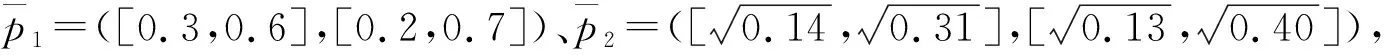
在现有得分函数和精确函数计算都存在一定特例难以区分IVPFN大小的情况下,Garg提出了现有方法并没有考虑区间犹豫度对IVPFN大小的影响,将区间犹豫度引入了精确函数中,定义了考虑区间犹豫度的精确函数:

(6)

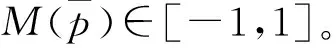
该函数中犹豫度越小,精确函数越大,体现了不论受支持或反对的事件必定期望其犹豫度越小越好。而在实际决策中,犹豫度一般受到隶属度和非隶属度的影响。隶属度占比越大,说明该事件受支持的概率更大,则犹豫度往往会偏向于支持,对隶属度存在一定的激励作用,反之亦然。式(6)这种判断方法并未考虑这一影响,故在一定条件下会存在与常理相悖的情况。

2.2 改进得分函数

通过对上述得分函数和精确函数的分析,现有研究主要存在以下不足:① 计算步骤多,遇到特殊情况,一般要通过3次计算判断才能区分IVPFN的大小;② 由于式(4)～式(6)都是通过平方计算对值进行比较的,一定程度上数值通过平方后会被压缩而偏小,值比较时差距也更接近,故依然存在一定的特殊情况无法区分;③ 式(6) 仅体现了受支持的事件必定期望其犹豫度越小越好,并未体现出犹豫度对隶属度或非隶属度的激励或惩罚作用。

为解决这一问题,本文提出一种改进后的新得分函数,既涵盖现有得分函数和精确函数的优点,又弥补其不足。

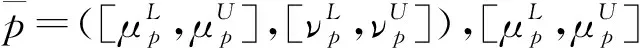
(7)

整体来看,改进后的新得分函数仅需要1步计算即可判断IVPFN的大小,不需要两次比较,也考虑了决策人一般都希望决策事件的犹豫度越小越好的心态和犹豫者的从众心理,解决了上述现有得分函数的问题。下面对改进后的得分函数相关性质和定理进行证明,以验证该函数的正确性。

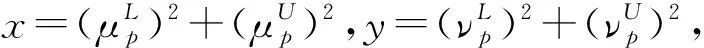
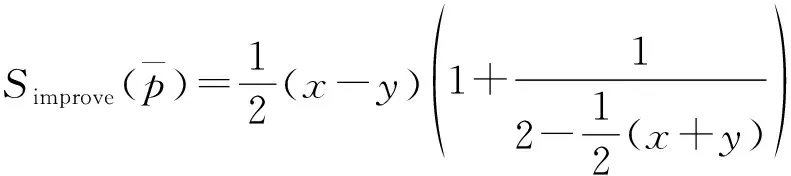
(8)

证毕

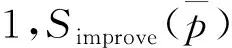
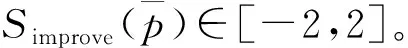
证毕

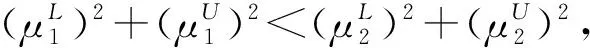
艺体类术课与技能技巧课程：不断加大学生自学自训的任务与要求，以获得核心技能技巧或技能技巧的核心环节在技能技巧形成过程中的迁移能力并进行自学自训为主要目标。

证毕

3 基于前景理论的区间值毕达哥拉斯模糊TOPSIS法

根据本文提出的改进后新得分函数的相关定义和性质,可将IVPFN转换为改进后的得分函数,从而开展决策工作。而区间值毕达哥拉斯模糊多属性决策一般都是假设决策人完全理性的,但在实际决策中,人是有一定的主观判断和非理性心理的,尤其是对风险的偏好所造成的得失心理对决策影响较大。因此,依据本文提出的新得分函数,利用前景理论考虑决策人的主观感受,提出了基于改进得分函数和前景理论的区间值毕达哥拉斯模糊TOPSIS法,具体描述如下。

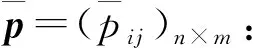
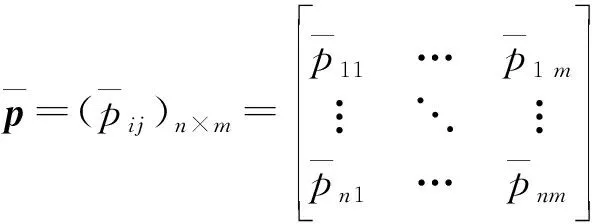
(9)

(10)

确定正理想方案和负理想方案相对应的得分函数集()、()。由于得分函数已将区间模糊数精确化,且具有一定的单调性,故不需要再对效益型属性和成本型属性进行区分,可直接得出()、()如下:

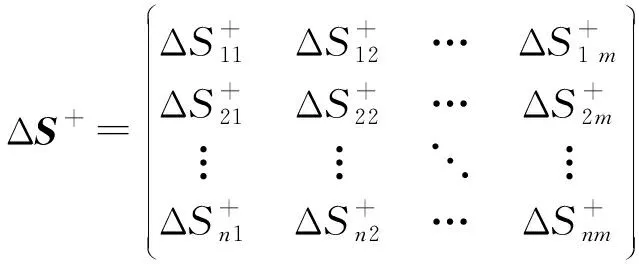
令Δ表示各个备选方案与正理想方案得分函数集()的贴合矩阵如下:

(11)

由于各备选方案相对于正理想方案的贴合度表示损失值,相对于负理想方案的贴合度表示收益值,则根据前景理论价值函数的定义,结合各属性权重由式(3)可得各备选方案的综合损失值()和综合收益值() 如下:

(12)

(13)

由文献[16]可知,根据经验数据,一般取==088、=225。

4 算例分析

算例分为两部分:① 以校企间研发项目合作为对象,利用本文方法对备选研发项目进行多属性决策,得出项目排序以供校企合作参考,验证本文方法的正确性和适用性;② 以上述数据为基础,将本文方法与基于原得分函数的区间值毕达哥拉斯模糊多属性决策方法,即式(4)相对比,验证本文方法的有效性。

4.1 多属性决策应用

为进一步促进科研成果转化,加强校企合作,某高校和企业之间计划开展一系列研发项目,现有4个备选研发项目={,,,},依据5个决策属性战略、技术、经济、资源、风险开展多属性决策,属性权重已知且相等,均为02。

首先,以区间值毕达哥拉斯数给出各备选研发项目在各属性下评价信息,如表1所示。

表1 备选研发项目在各属性下的区间值毕达哥拉斯数评价信息Table 1 Evaluation information of interval Pythagorean number under each attribute of candidate research and development projects

再次,确定正负理想研发项目的得分函数集()=(1860,0228,1295,1045,0334)、()=(-1846,-1686,-0769,-1417,-1846),继而由式(11)得出贴合矩阵Δ、Δ,根据式(12)和式(13)得出各备选项目的综合损益值和综合损益比如表2所示。

表2 备选研发项目综合损益值Table 2 Comprehensive profit and loss value of alternative research and development projects

最后,根据综合损益比对各备选项目进行排序,顺序为>>>,最佳项目为。根据结果进行分析,可以看出本文方法能有效区分各备选研发项目,得出其中比较具有优势的项目,差异度明显,验证了本文方法的正确性和有效性。

4.2 得分函数改进前后对比分析

为进一步验证本文方法的有效性,采用第4.1节原数据,基于原得分函数式(4),以第3节方法为依据开展多属性决策得出各备选项目综合损益值和综合损益比,如表3所示。

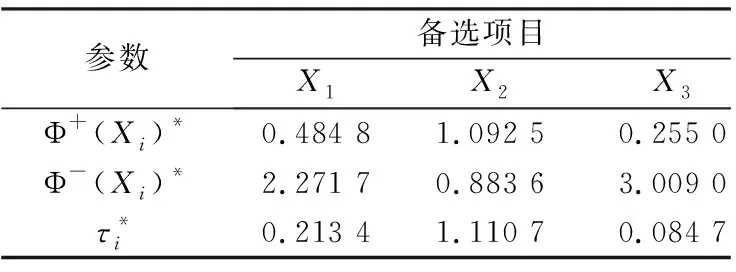
表3 基于原得分函数的备选研发项目综合损益值Table 3 Comprehensive profit and loss value of the candidate research and development projects based on the original score function

根据综合损益比,同样得出排序为>>>,最佳项目为,与本文方法一致。对两种方法所得综合损益比进行分析,如图1所示。

图1 得分函数改进前后综合损益比对比图Fig.1 Comparison chart of comprehensive profit-loss ratio before and after score function improvement

对图1进行分析可以看出,虽然两种方法所得项目排序一致,但基于原得分函数的计算方法所得各项目综合损益比值之间的差距较小,难以确定最佳项目。在特定情况下,可能会存在各项目综合损益比难以区分的问题。而本文方法最佳项目的区分度较为明显,综合损益比远大于其他备选项目,具有较高的有效性。

5 结 论

本文针对多属性决策过程一般未考虑决策人偏好习惯的问题,在区间值毕达哥拉斯模糊环境下引入前景理论,为解决现有得分函数忽略区间犹豫度对决策影响的情况,对得分函数进行改进,在假设决策权重已知的前提下,提出了基于改进得分函数和前景理论的区间值毕达哥拉斯模糊多属性决策方法。

与以往研究相比,本文研究的主要创新之处为:① 针对现得分函数的不足,考虑区间犹豫度对多属性决策的影响,提出了一种改进后的新得分函数,并证明了相关定理和性质;② 针对以往决策中假设决策人一般都是完全理性的,引入前景理论价值函数来体现决策人由于损益表现出的主观感受价值;③ 借鉴TOPSIS法,优化多属性决策流程,利用综合损益比来进行方案排序优选,更符合实际决策过程。