基于频控阵MIMO雷达的低复杂度稳健波束形成算法

刘奕彬, 王春阳, 宫 健,*, 谭 铭

(1. 空军工程大学防空反导学院, 陕西 西安 710051;2. 国防科技大学信息通信学院, 湖北 武汉 430010)

0 引 言

相控阵形成的波束由于无法分辨主瓣范围内不同距离的目标,因此在抑制与距离相关的干扰方面存在局限性。频控阵(frequency diverse array, FDA)由Antonik等在2006年IEEE雷达国际会议上首次提出,其独特的阵列特性一经提出就得到了国内外学者的关注。与相控阵不同, FDA通过在阵元间引入一定的频偏增量,使其波束方向图具有时间-距离-角度相关特性。通过与多输入多输出(multiple input multiple output, MIMO)技术结合,FDA-MIMO雷达能够在接收端形成等效的发射天线方向图,可以将发射信息整合到接收端,从而实现更加灵活的距离维自由度利用并提升距离-角度二维联合信号处理的能力。充分利用FDA-MIMO的距离-角度二维相关特性,可以实现距离-角度二维目标定位、抗主瓣假目标干扰等。

自适应波束形成是一种常用的空域自适应滤波算法,能够通过自适应地调整阵列天线的权值进而对干扰进行自适应地抑制。但自适应波束形成算法往往对阵列失配具有较高的敏感度,这将导致算法的性能急剧降低。稳健自适应波束形成算法的提出极大地提高了自适应波束形成对阵列失配的鲁棒性,但这些算法中仍存在需要改进的地方。在对角加载算法中,在输入信噪比(signal to noise ratio, SNR)较高时将会出现对期望信号的“自消”现象,同时最优对角加载因子的选择仍是一个需要研究的问题。特征空间法能有效降低噪声子空间扰动带来的不利影响,但在低输入SNR条件下的子空间塌陷现象将导致算法性能严重下降。基于最差性能最佳化(worst-case performance optimization, WCPO)的算法能有效应对导向矢量随机误差的问题,但算法中的误差范数上界与真实导向矢量失配范数不匹配时,算法的稳健性将严重降低。为能根据真实导向矢量失配范数的变化而自适应地设置误差范数上界,一种基于期望信号无失真响应的概率约束 WCPO 算法被提出来以获得与真实导向矢量失配范数更匹配的等效误差范数约束上界,从而改善 WCPO 算法的保守缺点。

以上对自适应波束形成的研究一般基于相控阵体制,因此将自适应波束形成技术应用于FDA体制对于抗干扰技术的拓展具有重要意义。目前,基于FDA的干扰与抗干扰技术受到学者的广泛关注和研究,文献[25]提出了一种基于FDA-MIMO雷达体制的距离维干扰抑制自适应波束形成方法,使得目标定位性能得到了进一步提升。文献[26]提出了一种主瓣保形功能的稳健波束形成方法,有效提升了抗杂波干扰性能。对于量化误差、角度误差与频率增量误差等降低干扰抑制性能的因素,文献[27]提出了一种在等效发射天线方向图的零点附近人工加宽零陷的波束形成方法。文献[28]通过对多种稳健波束形成算法进行分析,提出了一种强稳健性的改进特征空间(eigenspace-based, ESB)算法,但算法的核心仍是对角加载处理,并未充分利用特征子空间的优势。因此,本文通过分析FDA-MIMO雷达体制下的各类稳健波束算法的优势与不足,提出了一种低复杂度的稳健波束形成算法,在低采样快拍数和低SNR条件下均具备良好的鲁棒性,为技术实现提供一定的参考意义。

本文的内容架构如下:首先介绍了FDA-MIMO雷达的信号处理模型,其次对经典的稳健自适应波束形成算法进行了分析,进而提出一种低复杂度的稳健波束形成算法并证明了方法的合理性,然后通过仿真实验对比了各算法在FDA-MIMO雷达中的波束性能,进而验证了所提出方法的优越性,最后对全文工作进行了总结。

1 FDA-MIMO信号模型

考虑一个发射和接收阵列均为均匀线阵FDA-MIMO方案,其结构如图1所示。

图1 FDA-MIMO雷达的结构示意图Fig.1 Schematic diagram of FDA-MIMO radar structure

发射阵列的相邻阵元间的间距为,接收阵列的相邻阵元间的间距为。发射阵列和接收阵列的阵元数分别为和。第一个阵元为参考阵元。发射载频为,第个阵元的发射信号可以表示为

(1)

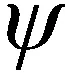
(2)

式中:[·]为共轭运算。

对于坐标位于(,)的目标点,与第个发射阵元和第个接收阵元相关的接收信号可以表示为

(3)

式中:,为从第个发射阵元到第个接收阵元的传播时延,可以表示为

(4)

式中:c为光速。

由于考虑了往返双程距离,在远场窄带条件下,式(3)可以近似表示为

(5)

式中:()可表示为

(6)

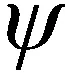
图2 接收端的信号处理步骤Fig.2 Signal processing steps at the receiver

于是,与第个发射阵元和第个接收阵元相关的输出信号可以表示为

(7)

式中:为经过匹配滤波后的信号复系数;′=-2c。于是,阵列因子可以表示为

(8)

于是,导向矢量可以表示为

=(,)⊗()

(9)

式中:⊗为Kronecker积,(,)和()作为发射和接收导向矢量可以分别写为

(10)

(11)

由式(10)可知,在FDA-MIMO体制下,发射导向矢量是与距离参数相关的,时间参数被成功消去。当探测一个坐标为(,)的远场点目标时,权矢量应设置为

=|=,==(,)⊗()

(12)

则发射-接收天线方向图可以表示为

(13)

式中:[·]为共轭转置运算。根据发射端和接收端产生的不同效果,发射-接收天线方向图可以进一步分解为发射方向图和接收方向图。需要注意此处的发射天线方向图是接收端的等效发射天线方向图,可以表示为

=

(14)

可知,距离剖面的波束主要受频偏设置的影响,当采用线性频偏时,式(14)可改写为

(15)

从上式可知,线性频偏的波束在距离维度上存在周期性,周期为=cΔ。同理,接收天线方向图可以表示为

(16)

由此,通过采用接收端多匹配滤波器的FDA-MIMO方案产生的天线方向图是具有距离相关性的时不变波束。

2 稳健波束形成算法

本节中将介绍对角加载(loading sample matrix inversion, LSMI)算法等。

2.1 LSMI算法

最小均方无畸变响应(mimimum variance distortionless respinse, MVDR)准则在不存在期望信号导向矢量误差的情况下能形成最优波束,但在采样协方差矩阵中含有的期望信号会导致信号自消现象的产生。LSMI算法是在MVDR的基础上对采样协方差矩阵进行对角加载,则FDA中带约束的MVDR优化问题可以表示为

由拉格朗日乘子法解得

(17)

LSMI算法相当于给环境中添加了白噪声,通过减小实际信号的SNR减弱最小化目标函数对信号的抑制并增强对噪声的抑制,信号的自消程度得到减弱,并达到了降低和稳定旁瓣的效果。LSMI算法的缺点是无法在实际环境中确定最优加载量,加载量过小将无法形成稳健波束,而加载量过大将影响对干扰的抑制效果。

2.2 ESB算法

ESB算法的核心是将期望信号导向矢量向干扰和信号特征子空间投影,进而实现改善信号自消的效果。将采样协方差矩阵进行特征值分解为

=+

(18)

式中:是信号和干扰特征向量构成的矩阵;是信号和干扰特征值构成的对角矩阵;是噪声特征向量构成的矩阵;是噪声特征值构成的对角矩阵。将期望信号的导向矢量向干扰和信号特征子空间投影后得到的FDA自适应权矢量为

(19)

式中:=为干扰和信号子空间的投影矩阵。ESB算法在高SNR的情况下能有效地抑制由导向矢量失配引起的信号自消现象。但在低SNR条件下,子空间缠绕导致不能有效分离出干扰和信号子空间,波束的性能降低。

2.3 WCPO算法

方向图的不稳健主要是由导向矢量失配引起,WCPO算法的核心是构造一个使期望信号导向矢量尽可能无衰减通过的自适应波束形成器,同时该波束形成器可使得其他方向的干扰和噪声功率最小。考虑实际信号的导向矢量为,期望信号导向矢量为,可将表示为

=+

(20)

式中：表示导向矢量的误差。权矢量的求解可表示为

可以由拉格朗日乘子法解得

(21)

式中:≥0为拉格朗日乘子,通过将式(21)代入等式约束条件进行迭代可以求解出的值,进而求解出最优权矢量。然而在实际应用中,导向矢量的误差上界无法确定,过大将导致主瓣变宽,分辨率降低;而过小将使得导向矢量误差时的波束无法保持稳健。

3 低复杂度稳健波束形成算法

本文提出了一种低复杂度稳健波束形成算法,能在低SNR与高SNR的条件下使波束均具有很好的稳健性。文献[28]提出了一种改进的ESB波束形成算法,通过干扰子空间重构协方差和对角加载电平实现了低SNR条件下的波束保形效果,其自适应权矢量为

(22)

式中:是干扰特征向量构成的矩阵;是干扰特征值构成的对角矩阵。该算法的核心是利用协方差矩阵中的干扰子空间,将协方差矩阵重构为

(23)

本文基于采样协方差矩阵,将新的协方差矩阵重构为

=

(24)

式中:为采样协方差矩阵。此时的矩阵近似为奇异矩阵,为使算法求逆环节有效,在矩阵求逆环节引入对角加载电平,则FDA的自适应权矢量为

(25)

可以发现,相比于改进的ESB算法,本文提出的算法中将进行求逆的矩阵由+ζ替换为了+ν,方法的合理性证明如下。

由于算法中重构的协方差矩阵和均为Hermitian矩阵,因此考虑加载电平之后存在等式:

+ν=+ζ+

(26)

式中:表示等式两边的差异矩阵,属于Hermitian矩阵。于是式(26)可以简写为=+。根据矩阵求逆法则,可将所提出方法中的求逆过程表示为

(27)

(28)

将式(28)代入自适应权矢量可得

(29)

因此,本文提出的算法仅基于采样协方差矩阵与其共轭转置实现了协方差的重构,相比文献[28]简化了特征值分解构建干扰子空间这一步骤,由此得到的低复杂度波束形成算法的具体步骤如下:

权矢量初始化,发射阵列向目标空域发射信号;

将接收到的目标相关数据在FDA-MIMO的接收端进行下变频、数模转换和多匹配滤波处理,使等效波束仅与距离角度相关;

将采样协方差矩阵与其共轭转置进行相乘得到重构得协方差矩阵,在对角加载固定电平后根据MVDR准则求解自适应权矢量。

输出信干噪比(signal to interference plus noise ratio, SINR)随输入SNR的变化曲线可以用于检验不同算法下FDA-MIMO雷达的目标探测性能,输出SINR可表示为

(30)

式中:表示通过不同算法得到的权矢量;和+分别表示期望信号的协方差矩阵和干扰加噪声协方差矩阵。

对于发射阵元数为、接收阵元为的FDA-MIMO雷达,其满自由度为,则各算法的计算复杂度如表1所示。相比于WCPO算法与其他基于ESB的算法,本文提出的算法省去了迭代计算与矩阵分解等步骤,计算复杂度得到了有效降低。

表1 计算复杂度对比Table 1 Comparison of computational complexity

4 仿真实验

实验采用的仿真参数如表2所示,通过对接收数据进行处理,FDA-MIMO雷达将在空域内产生距离-角度相关的二维自适应波束,以达到抑制干扰的效果。仿真中干扰信号的干噪比(interference-to-noise ratio, JNR)均被设置为60 dB,便于对比波束对各干扰信号的抑制性能。

表2 仿真参数Table 2 Simulation parameters

续表2Continued Table 2

4.1 LSMI波束形成器

实验考虑空域内存在多假目标的情况,当目标SNR为0 dB且存在5°导向矢量失配的情况下,LSMI算法的波束方向图如图3所示。图3中绿色圆圈标明了目标的实际位置,红色圆圈标明了多假目标的实际位置。由图3可知,尽管导向矢量存在失配的情况,LSMI算法仍能通过在假目标位置形成零陷来抑制干扰。

图3 LSMI算法方向图Fig.3 Beampattern of LSMI algorithm

由图4可知,当目标SNR提高到20 dB时,波束方向图在目标位置产生了零陷,这是由于回波中的目标信号将导致波束形成过程中发生信号自消现象,这显然不利于空域中对目标的指示。

图4 高SNR条件下LSMI算法方向图Fig.4 Beampattern of LSMI algorithm with high SNR

4.2 ESB波束形成器

利用特征子空间法产生的波束方向图如图5所示。在较高的输入SNR条件下,ESB算法产生的波束在导向矢量失配的情况下具有较好的稳健性,但由图6可知,在低输入SNR的条件下,ESB算法将产生严重的波束畸变,这使得波束性能大幅度降低。

图5 5°导向矢量失配条件下ESB算法方向图Fig.5 Beampattern of ESB algorithm with 5° steering vector mismatch

图6 低SNR条件下ESB算法方向图Fig.6 Beampattern of ESB algorithm with low SNR

4.3 WCPO波束形成器

图7给出了低采样快拍条件下WCPO算法产生的波束,考虑采样快拍数为200且导向矢量失配5°的情况,基于WCPO算法的波束在导向矢量失配时具有一定的稳健性,但低采样快拍数将导致基于该算法的波束旁瓣显著提高,波束的稳健性将受到影响。

图7 低采样快拍下WCPO算法方向图Fig.7 Beampattern of WCPO algorithm with low sampling snapshot

4.4 提出的波束形成器

通过以上分析可知,LSMI算法在高SNR条件下将出现信号自消现象,且存在对角加载量难以确定的特点;传统ESB算法虽然在高SNR条件下具备较好的稳健性,但在低SNR条件下波束将产生严重畸变;WCPO算法对导向矢量失配具有一定稳健性,但低采样快拍数的情况会使旁瓣升高。图8给出了基于本文提出算法的SNR=-20 dB时低采样快拍数的波束方向图。可见相比之前的传统方法,本文提出的方法在低SNR和低采样快拍数的极端条件下仍具备较好的波束保形能力,弥补了ESB算法在低SNR条件下的不足,在考虑低采样快拍数的情况下也体现出了优越性。

图8 低SNR低采样快拍下本文方法方向图Fig.8 Beampattern of proposed method with low SNR and low sampling snapshot

图9给出了方向图在目标位置的距离维剖面对比,通过对比图9(a)和图9(b)可知,ESB算法在低SNR条件下性能严重下降,这是子空间缠绕导致不能有效分离出干扰和信号子空间的结果。通过对比图9(a)和图9(c)可知,在低采样快拍数的条件下,样本矩阵求逆(sample matrix inversion, SMI)算法、LSMI算法和WCPO算法对应的波束旁瓣均发生了不同程度的升高,波束的稳健性出现下降趋势,而基于本文方法的波束在低SNR和低采样快拍数的条件下均具有良好的稳健性,体现了本文方法的优越性。值得注意的是,由式(15)得到的波束在距离维度上的周期性可以在波束剖面图中清楚展现,在距离接近200 km时,波束的增益显著上升并接近峰值,这与理论峰值位置的210 km保持了一致。

图9 目标位置方向图的距离维剖面对比Fig.9 Comparison of the profile of the target position pattern in range dimension

4.5 算法性能对比

图10将3种存在对角加载操作的方法进行了对比,可知本文提出的方法在加载电平处于-300 dB到100 dB之间均可以保证良好的输出性能,对角加载电平的可选择范围明显超过LSMI算法和文献[28]提出的改进ESB算法,体现了本文方法在加载电平上的选取优势。

图10 输出信干噪比-加载电平曲线Fig.10 Output SINR-loading level curve

图11中给出了不同采样快拍数下不同波束形成算法的输出SINR随输入SNR变化曲线,其中SMI算法不考虑导向矢量失配的情况,作为理想参照与其他算法性能进行对比,其他算法均考虑存在5°的导向矢量失配的情况。由图1中曲线可知,本文提出的方法在低采样快拍数条件下仍能稳定输出SINR,弥补了其他方法在低采样快拍时波束性能下降的缺陷。低SNR条件下,提出的方法与复杂度更高的WCPO算法具有接近的输出SINR,但极大程度上降低了波束形成的计算复杂度。高SNR条件下,提出的方法有效克服了信号高SNR时的自消现象,能够比LSMI算法和WCPO算法输出更稳定的SINR,相比于同样具有稳健性的ESB算法,本文所提出的算法减少了特征值分解这一步骤,使得形成稳健波束的复杂度进一步降低。

图11 输出SINR-输入SNR曲线Fig.11 Output SINR-input SNR curve

图12通过对比各算法在导向矢量存在误差时的输出SINR,对提出方法的稳健性进行了进一步验证。仿真采用2 000个采样快拍,通过设置SNR=-20 dB和SNR=0 dB两种情况分别进行200次蒙特卡罗仿真。由图12可知,在高SNR条件下,本文算法的稳健性明显优于LSMI算法和WCPO算法。而在低SNR条件下,所提方法也有效弥补了子空间缠绕导致的波束畸变的缺陷,以最低的计算复杂度实现了稳健波束形成。

图12 输出SINR-角度误差曲线Fig.12 Output SINR-angle error curve

5 结 论

本文提出了一种基于FDA-MIMO雷达的低复杂度稳健波束形成方法。针对LSMI算法高SNR条件下出现信号自消、ESB算法低SNR条件下波束畸变和WCPO算法低采样快拍条件下旁瓣升高等问题,提出了一种适用于以上多种非理想条件的稳健波束形成算法,算法的优势可以总结如下:① 在高SNR条件下克服了信号自消现象,且在低SNR条件下波束保形能力强。② 相比于WCPO、扩展ESB和改进ESB等算法,无需进行凸优化、迭代运算、特征值分解和奇异值分解等操作,有效地降低了计算复杂度。③ 相比于其他需要加载电平的算法,所提方法的电平有效加载范围更广,便于加载系数的选择。④ 在低采样快拍的条件下克服了其他算法波束性能下降的缺陷。本文通过仿真验证了方法的有效性和优越性,为FDA-MIMO雷达波束形成的权矢量设计提供了参考。