从儿童“数数”说起*
——例谈“数数”的数学教育价值
2022-10-29丁元春
丁元春 白 静
(合肥市临泉路第二小学 安徽合肥 230011)
引言
“1、2、3、4、5……”还记得小时候一边掰着手指一边数数的场景吗?那一定是每个人都难忘的经历,尽管那时我们并不知道什么是数学。笔者近期连续观察了许多低年级的数学课堂,遗憾地发现教师常常忽略极具数学教育价值的“数数”活动。这值得进一步深思。我们必须要思考:儿童和数学相遇的起点在哪里?
显然,对于儿童,数数是自然而然发生的。起初是源于模仿,儿童并不理解数背后的意义;之后逐渐学会了数物体的数量,在数数的过程中将数与物体一一对应起来,此时的数学思维相比物体与物体的对应更抽象。因此,儿童最早接触数学学习是从数数开始的。数数可以发展学生的数感,积累数学学习活动的经验,提高运算能力和思维水平,感悟数学思想。教学中,教师应该因地制宜地组织有意义的数数活动,通过活动,培养儿童的数学核心素养。
一、数数,为“数感”找到着陆点
《义务教育数学课程标准(2011年版)》明确指出:“数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟。”著名数学家华罗庚也曾经说过:“数(shù)起源于数(shǔ),量(liàng)起源于量(liáng)。”笔者认为这里有一重意思就是:数感的发展起源于“数数”活动。因此,在实际教学过程中,教师设计一些有意义的数数活动,对于培养学生的数感有很大的帮助。
笔者在教学苏教版一年级下册“认识一百以内的数”时,就做过这样的设计:首先让学生估一估“今天带来的小棒大约有多少根”,说说是怎样想的。接着顺学而教,提出“你觉得谁估计的更准确?”,学生自然想到去数一数小棒的个数。此时教师建议:请你数给你的同桌听一听,看谁数得又快又好。在学生数完之后,请学生说一说是怎样数的。从学生的交流中可以发现,大部分学生是一个一个数的,也有两个两个数的。而且数完之后,小棒仍旧杂乱无章地放在一起。于是教师提出疑问:“怎样摆放小棒才能让别人一眼看清是多少呢?”学生结合之前的学习经验能自然而然地联想到:我们可以将10根小棒捆成一捆,有序摆放。学生通过充分经历数小棒的活动过程,感受数数方法的多样性以及优化数的方法,发展了数感。
上述案例中,学生的“数感”在数数活动中找到了着陆点。所以,在教学中,教师要积极地组织有价值的数数活动,将“数感”的培养贯穿课堂学习过程,为学生“数感”的发展插上飞翔的翅膀。
二、数数,让计算的种子生根发芽
数数与计算其实有着根本的联系,组织好“数数”活动既能帮助学生理解算理,还能提高运算能力。
苏教版一年级“认识一百以内的数”的学习中,教师设计了关于数数的几个课后练习(如图1-4):①数教室的桌子和凳子;②数不规则呈现的星星;③数十个一桶的羽毛球;④数五个一把的香蕉。
根据教材设计的习题,教师组织学生按群计数:数桌椅的个数是2个2个地数,每把香蕉是5个5个地数,数星星可以10个10个地圈一圈,还可以请学生尝试按群倒着数一数。按群数数足够熟练之后,学生再学习计算,便很轻松了。无论后面加1、加2或是加几,都可以通过数数迅速得到结果。计算成了数数的衍生品,20以内甚至100以内的加减法,学生也可以按照同样的方法得出结果。经历了按群计数的活动过程,乘法的学习水到渠成。

图1 图2

图3 图4
上述练习设计的主线是“数数”,通过数的过程,发展学生的“数感”,提升计算能力。数是为了不数。弗赖登塔尔指出,数数可以向前数,也可以向后数,可以按群计数,或者把数凑成整十整百的数数一数。这些练习可以与数轴结合起来进行。它能为心算做好准备,也能为笔算做好准备。
三、数数,让思维水平逐步提升
数数活动中蕴含着很多规律,学生通过观察发现规律后,若能通过语言说出来,思维水平就会进一步得到提升。
下面是一张百数表(见图5),仔细研究可以发现,数的排列是有着一定规律的,儿童通过数数活动,找出这些规律,不仅可以激发他们数数的兴趣,培养观察能力,而且能提升计算水平。更重要的是,在活动的过程中,学生的思维水平也会逐步提升。
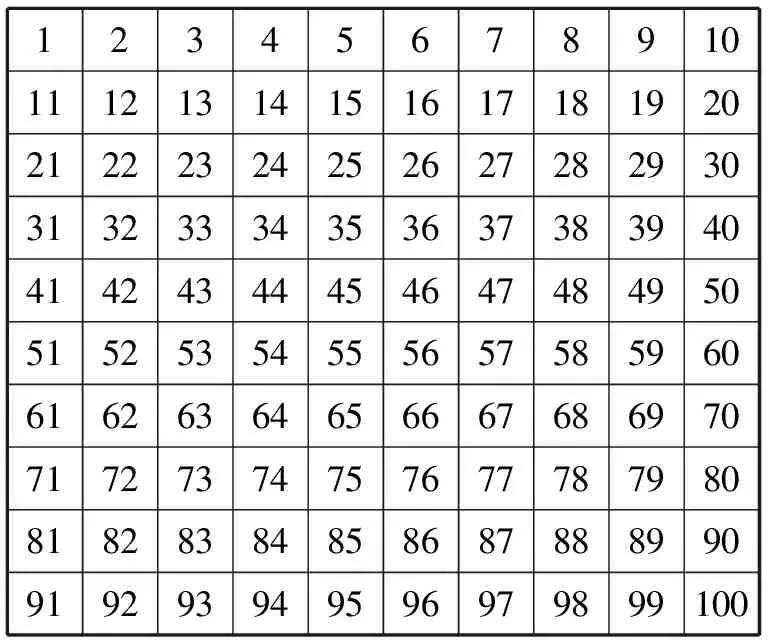
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
四、数数,让数学思想潜移默化地渗透
湖南第一师范学院的胡重光老师在《数数的数学教育意义》一文中举过这样一个案例:在采用蒙台梭利教学法的幼儿园里,教师会让五六岁的儿童在纸上从1开始按顺序写数。其中,有个儿童写到一千多的数时,就不愿继续往后写了,因为她觉得无论写多少,后面的数都是这样一直下去的。弗赖登塔尔认为这个女孩很了不起,因为她发现了“无限”的概念。“这正是数学的出发点和归宿。”
上述案例中,儿童在数数活动中发现了“无限”,并用自己的方式表达了出来,这是多么伟大的发现。其实,教师还可以让学生充分经历数数的活动,从中体会到“一一对应”和“有序”等数学思想,让数学思想通过有意义的数数活动扎根于课堂之中。
综上所述,儿童的数学学习是在数数中开始的,学好数学要从“数好数”开始。“数”最终是为了“不数”。在实际教学中教师要善于组织有意义的数数活动,让儿童在活动中真实自然地生长。
