井中地震黏声逆时偏移的井型影响分析

2022-10-28王霁川谷丙洛李振春

物探与化探 2022年5期

王霁川，谷丙洛，李振春

(中国石油大学(华东) 地球科学与技术学院，山东青岛 266580)

0 引言

目前，随着我国含油气盆地勘探程度的不断提高，勘探难度逐渐加大，复杂构造、复杂岩性、深层/超深层油气藏已逐渐成为主要勘探对象[1]，勘探的地质目标具有“隐、碎、薄、小”的特点，如复杂小断块、致密碎屑岩等[2-3]，对地震偏移成像技术提出了更高的要求。井中地震具有资料信噪比高、储层识别能力强的优点。此外，它能够适应检波器的任意排列，可减少面元数据体丢失，理论上能够对井周的“隐、碎、薄、小”等储集体实现高精度成像。

井中地震技术按照震源的类型可分为随钻井中地震和爆震井中地震。随钻井中地震，即依靠随钻地震的思想，利用钻头的振动作为震源进行井地观测[4]，基于该思想国内外很多学者对旋转钻头和随钻井中地震做了相关研究[5-9]。但随钻地震存在着探测深度有限的弊端，不利于深层复杂构造区域的地震勘探，由此发展了井中激发震源的爆震井中地震。对于爆震井中地震，由于其需要在保护井筒的同时激发出较强的能量，对震源的要求很高，因此相关研究较少且主要集中在浅层层析成像、煤层井中地震研究及工程物探领域[9-16]。在石油地震勘探领域，井中地震技术的研究相对较少。

在实际生产中，钻井的设计受到生产要求或客观因素影响，井型除常规的直井外还存在斜井、曲斜井、水平井等多种情况。与常规的直井相比水平井在非常规油气资源高效勘探和开发上有着重要的作用[17]。而在海洋勘探中，由于作业平台的空间有限，其井型一般都为有角度的斜井或空变的斜井[18]。由于井中地震的激发震源位于井中，不同井型使得震源所处空间位置有较大差异，造成地震波的传播路径存在显著不同，这势必会对最终的成像结果产生影响。因此在应用井中地震技术前，需详细分析井型对成像结果的影响，进而指导实际生产中激发井段的选择。

考虑到应用井中地震技术的目的是对深层复杂构造进行精细成像，对比常用的Kirchhoff积分偏移、单程波偏移、逆时偏移等成像算法，逆时偏移算法具有没有角度限制、适合复杂介质成像的优势。此外，由于震源位于地下，能量微弱受地层吸收衰减作用影响严重，地震波在传播过程中会伴随着能量衰减和波形畸变现象，影响偏移剖面精度。综合以上因素，对于井中地震，应对其进行Q补偿逆时偏移成像，以而获得高保真度的偏移成像剖面。

早期的衰减补偿是对地震记录应用反Q滤波达到波场放大的目的[19-20]，主要用于Kirchhoff偏移和单程波偏移中[21-22]，但仅是对振幅相位进行逐道补偿，没有考虑地震波传播路径问题，因此无法达到合理的补偿效果。而基于黏滞波动方程的Q补偿偏移可以在波场延拓过程中进行补偿，更具有说服力。目前基于标准线性固体(SLS)模型的方程被广泛使用，用以描述衰减过程[23-24]，许多学者对其进行了相关研究并最终实现了稳定的Q补偿逆时偏移(Q-RTM)[25-27]。总体来说基于SLS模型的方程，具有计算速度快、便于实现的优点，但同时也存在衰减项和频散项相互耦合的缺点。为解决这一弊端，诸多学者发展了以常Q模型为基础的方程[28-29]。其中，Zhu等[30]、吴玉等[31]基于平面波频散关系提出了解耦的分数阶黏声波方程，该方程显式分离了衰减项和频散项，同时对振幅和相位进行了校正，具有较高的精度，且在West Texas实际数据中[32]进行了应用，并取得了良好的效果。但其同样存在需要利用伪谱法求解Laplace算子，计算量大，衰减和频散项解耦不彻底的问题。基于该方程国内外诸多学者进行了一系列研究[33-39]，总的来说解耦的分数阶Laplace 方程具有较高的计算精度，便于实现稳定的Q-RTM。

综上所述，井中地震是一种可以实现对井周“隐、碎、薄、小”地质目标进行精细成像的物探方法。在实际生产中，井型不同对成像结果存在影响，然而，当前井型对于偏移成像的影响具体如何，还没有定性或定量的认识。本文使用黏声逆时偏移方法进行井中地震成像，并基于Zhu等[30]提出的分数阶黏声波方程进行数值模拟，通过在理论模型中进行直井、斜井、曲斜井、水平井与多井的成像试算，探究井型对偏移质量的影响。数值实验结果阐明了井型与成像剖面间的影响关系，为井中地震采集系统设计提供了理论支撑。

1 井中黏声逆时偏移基本原理

1.1 井中地震特点

井中地震技术是一种井中激发，地面接收的特殊物探方法。由于井中地震观测系统特殊，导致其与地面地震存在较大差异，地面和井中地震观测系统如图1所示。从图中可见，与地面地震相比，由于井中震源位于地下且靠近勘探目标，故其激发的地震波减少了一次低降速带损耗，规避了面波的产生，有助于采集高分辨率及信噪比的地震信号；同时由于井中地震在地面上不存在震源干扰，因此，在地表可进行大范围检波器布置，有利于进行高密度采集；且可以采用规则化观测系统在地面布置检波器，以降低面元数据体丢失，便于在采集区域获得更丰富的有效信息。

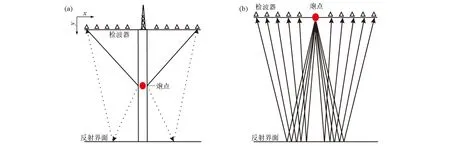
图1 井中地震(a)与地面地震(b)观测系统示意Fig.1 Schematic diagram of 2D borehole seismic(a) and ground seismic(b) observation system

井中地震由于震源位于井中，因此当震源位于不同井型时，地震波的传播路径也不尽相同。不同井型地震波的传播路径如图2所示。通过对图2a、b、c的对比发现，直井与曲斜井和水平井的地震波传播路径主要差异在于偏移距的变化，由于波的传播路径不同故其偏移距也不同。综合以上分析可以发现，井型的变化主要影响了地震波的传播路径，进一步对偏移距产生了影响。考虑到井中地震的偏移距大小与反射点覆盖范围密切相关，因此在理论上井型的变化会对最终成像剖面的成像范围产生影响。

a—直井路径示意；b—曲斜井路径示意；c—水平井路径示意a—schematic diagram of vertical well path；b—schematic diagram of curved inclined shaft path；c—schematic diagram of horizontal well path图2 井中地震地震波的传播路径示意Fig.2 Propagation path of seismic wave in well

尽管井中地震技术具有诸多优点，但其同样存在受地层衰减效应影响大，采集的地震数据层间多次波干扰严重、覆盖范围有限的缺点。总体来说，在理论上井中地震技术是一种适用于井周区域小构造精细勘探的特殊物探方法。

1.2 分数阶黏声波方程

在地震勘探领域，介质的衰减特性通常被认为与频率呈线性关系。因此，在地震资料频带范围内，可以假定Q与频率无关，即常Q模型。基于此假设，Kjartansson[28]推导了常Q模型的速度相位频散和衰减关系：

(1)

(2)

式中：ω0是参考角频率；ω是角频率；c0是参考角频率对应的声波速度；cp是声波速度；γ=tan-1(1/Q)/π，是无量纲参数；α是衰减因子。基于上述常Q频散关系，Zhu等[30]推导了时间域分数阶黏声波方程：

(3)

其中

(4)

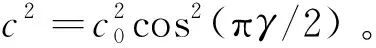
对于方程的稳定性问题，本文通过对方程(3)的左侧进行广义傅里叶变换，并对二阶时导数进行中心差分。下一时刻的波场pn+1可以由当前时刻的波场p和前一时刻的波场pn-1表示如下：

(5)

矩阵的形式如下：

(6)

其中

(7)

本文使用特征值法分析介质波动方程的稳定条件，方程若保持稳定则其矩阵的特征值必须小于或等于1，故通过对式(6)的特征值求取可得，分数阶方程的稳定性条件为：

(8)

为了保证解对所有波都是稳定的，c0=cmax是最大速度，k=π/Δx是奈奎斯特空间波数，此时γ=tan-1(1/Qmin)/π 。

为了便于实现基于上述方程的黏声逆时偏移，本文使用统一的黏声波方程进行波场的正向和反向延拓，具体如下：

(9)

方程(9)右端第二项和第三项分别为表示相位频散和振幅衰减。其中，β1可以取1和0，β2可以取1、0和-1。对于相位频散项，β1取1表示包含相位频散，β1取0表示无相位频散。对于振幅衰减项，β2取1表示振幅衰减，β2取0表示无振幅衰减，β2取-1表示振幅衰减补偿。

基于上述分析，Q补偿逆时偏移需包含相位频散项，而且需对振幅衰减进行补偿，也即β1=1，β2=-1，则方程(9)可重写为：

(10)

本文利用方程(10)进行波场的正向和反向延拓，校正地震波传播过程中的振幅衰减和相位频散。

1.3 Q补偿逆时偏移原理

叠前逆时偏移分为3个步骤：①震源波场正传；②检波点波场反传；③应用成像条件成像。在波场模拟的过程中本文选用Liu等[40]的混合吸收边界作为边界条件，该方法将计算区域分为内部区、过渡区和边界区。在进行波场模拟时，内部区中用双程波方程求解，边界区用单程波方程求解，过渡区波场由单程波和双程波的波场加权得到；在成像条件的选取上，本文选用了在成像过程中同时利用了震源波场和检波点波场的信息，可以对所有波进行成像的互相关成像条件。互相关成像条件可表示为：

(11)

式中：I(x)表示成像结果；S(x,t)和R(x,t)分别表示t时刻成像空间x处的震源波场和检波点波场；x=(x,y,z)表示成像点空间位置矢量；T为最大记录时间。

图3为井中地震波场正向延拓及逆时偏移原理示意。其中图3a、b分别表示无衰减和衰减介质波场正向延拓过程。对于衰减介质，波场正向延拓过程中振幅的衰减情况可以表示为：

a—无衰减介质波场正向延拓；b—衰减介质波场正向延拓；c—声波逆时偏移；d—Q补偿逆时偏移a—forward continuation of wave field in non attenuating medium；b—forward continuation of wave field in attenuating medium；c—acoustic inverse time migration；d—Q compensation inverse time migration图3 井中地震波场延拓及逆时偏移原理示意Fig.3 Principles of wavefield propagation and reverse time migration in boreholes seismic

(12)

式中，LD和LU分别表示波场下行和上行传播距离。

由于实际地层是一种黏弹性介质，当地震波在黏弹性介质中传播时，波场的振幅和相位会发生变化，最终影响成像剖面。图3c、d分别表示声波逆时偏移和Q补偿逆时偏移的基本原理。对于衰减介质，需在震源波场正向延拓和检波点波场反向延拓过程中进行补偿，基于图3b所示的地震波场衰减规律，Q补偿逆时偏移过程中，任意成像点处的震源波场和检波点波场可分别使用算子e+αLD和e+αLU进行衰减补偿，具体可以表示为：

SC(x,t)=S(x,t)e+αLD,

(13)

(14)

利用补偿后的震源波场SC(x,t)和检波点波场RC(x,t)，应用零延迟互相关条件实现成像，具体为：

孩子不知道，最大的美是自由，自由才会让生灵展现出多姿多彩的美丽。一旦失去了自由，那美也就没有了灵动之气——比如蝴蝶，比如人。

(15)

结合式(12)、(14)和(15)，由零延迟互相关成像条件得到的补偿后图像IC(x)理论上等于声波逆时偏移得到的图像I(x)，即介质的吸收衰减效应得到完全补偿。

当不考虑地层的黏滞性时波场正向延拓和逆时延拓在参数选取合理的情况下都是稳定的。但当地震波在黏滞性介质中传播时，由于波场正传过程是一个能量衰减过程，故该过程稳定。但在逆时延拓的过程中，黏滞波动方程会对震源和检波点波场进行补偿，使其能量呈指数型增大，与此同时波场中高频噪声也被呈指数放大，因此出现高频不稳定现象。为保证波场的稳定[30]，通过在波数域设置低通滤波器将高频噪声去除。与此同时，本文考虑到在应用互相关成像条件进行逆时偏移成像时，成像过程中存在低波数噪声干扰现象。因此本文通过在成像剖面应用Laplace滤波的方式来压制低波数噪声。

在偏移成像过程中由于井中地震特殊的观测方式，导致其成像范围有限，有效成像范围近似为“拱形”。图4a为水平层状介质中，井中地震射线路径示意，从图中可以发现，对于井中地震数据，不同采样点对应的反射点位置在水平方向和深度方向均有变化，反射点轨迹成“拱形”。随深度增加，反射点位置逐渐远离震源，到达最深位置时，反射点与震源相距最大，水平距离为偏移距的一半。由此可见，当震源深度一定时偏移距越大，反射点水平方向覆盖范围越大；图4b为不同激发深度覆盖范围分布，可以看到当震源处于不同深度时，其覆盖范围也有所差异。当检波器排列固定时，震源深度越大，其覆盖范围越小，最大覆盖范围为一半炮检距，此时震源位于井口[13]。

图4 井中地震射线路径(a)及不同激发深度覆盖范围(b)示意Fig.4 Seismic ray path(a) and coverage map with different excitation depth(b) in well

2 数值模拟

2.1 井中地震数值模拟

本文选用砂泥岩薄互层模型应用声波和黏声波方程进行数值试验，图5为所用模型，大小为242×600，深度方向采样间隔为5 m，水平方向采样间隔为10 m。采用主频为20 Hz的雷克子波作为震源，记录时长为5 s，采样间隔为0.5 ms，共设置242个检波器均匀分布于地表，道间距为10 m。为了压制震源引起的强照明现象，本文采用设置衰减因子的方式对震源处能量进行压制，而由于井口距检波器位置较近，衰减因子的影响导致成像剖面井口处存在一定的能量不均匀现象。

图5 砂泥岩薄互层速度模型(a)和Q模型(b)Fig.5 Veolocity model(a) and Q model(b) of sand-shale thin interbed

图6为井中地震逆时偏移剖面，激发井段长度为1 000 m，炮数20炮，炮间隔50 m，由水平方向1 200 m深度300 m处自上而下依次激发，图中红色竖线代表井位，图6a～c分别为声波偏移剖面，黏声未补偿偏移剖面，黏声补偿后偏移剖面。本文选用不考虑衰减情况的声波逆时偏移结果(图6a)作为参考剖面，通过对比未补偿和补偿后偏移结果可见，成像剖面与理论预期相符。图6b为考虑了黏弹性介质的衰减影响，但未进行补偿的逆时偏移剖面，与参考剖面相比，该剖面能量明显减弱，且仅可对浅层进行成像，深度2km以下的薄互层区域难以成像，整体成像效果极差。图6c为补偿后的逆时偏移剖面，与图6b对比可以看出，补偿后的剖面消除了地层衰减作用对成像剖面质量的影响，解决了成像剖面能量弱的问题，同时对模型的浅、中、深层均进行了良好的刻画，结果与参考剖面相符。图7为与图6对应的薄互层模型局部偏移剖面，通过图7b、c的对比可以看出：地层的吸收衰减效应对薄互层影响严重，当未进行衰减补偿时，薄互层处能量弱，层位难以识别；补偿后的剖面能量得到恢复，层位刻画清晰与参考剖面(声波局部偏移剖面)结果相符。

a—声波偏移剖面；b—黏声未补偿偏移剖面；c—黏声补偿后偏移剖面a—acoustic migration profile；b—viscoelastic uncompensated migration profile；c—migration profile after viscoelastic compensation图6 薄互层模型逆时偏移剖面Fig.6 Reverse time migration profile of thin interbedded model

a—声波偏移剖面；b—黏声未补偿偏移剖面；c—黏声补偿后偏移剖面a—acoustic migration profile；b—viscoelastic uncompensated migration profile；c—migration profile after viscoelastic compensation图7 薄互层模型逆时偏移剖面局部放大Fig.7 Partial enlarged view of reverse time migration profile of thin interbedded model

通过对比图6a～c和图7a～c可得出以下结论：地层的吸收衰减效应会严重影响偏移剖面的成像质量，使目的层难以识别；采用稳定Q补偿的井中逆时偏移成像方法能够有效地补偿介质吸收衰减对成像结果造成的影响，改善成像质量。

2.2 井型影响因素分析

图8 薄互层模型逆时偏移参考剖面Fig.8 Reverse time migration reference profile of thin interbedded model

为探究当存在水平激发段时对偏移结果的影响，选用一个简单的井位布置形式，即在直井后增加一段水平井段，模拟实际生产中的激发井存在水平激发井段的情况。图9为补偿后的井中地震偏移剖面，直井井段中震源布置方式与图6中相同，在水平井段中震源炮间隔50 m，由左向右依次激发。图9a为水平井段长度为500 m的偏移剖面，炮数10炮；图9b为水平井段长度为1000 m的偏移剖面，炮数20炮。通过与参考剖面的对比可见，当存在水平井段时，偏移剖面照明范围有一定提升，但增长有限；通过图9a、b成像剖面对比可以看出，当水平井段长度增加时，其照明范围也随之扩大，但对薄互层处影响有限。当存在水平激发井段时，成像效果改善有限，仅在照明范围方面有一定变化。考虑实际生产成本及震源放置的难易程度问题，本文认为在井中地震资料的采集过程中，水平井段并不适合作为激发井段。

a—水平井段500 m；b—水平井段1 000 ma—horizontal well section with 500 m；b—horizontal well section with 1 000 m图9 薄互层模型水平井逆时偏移剖面Fig.9 Reverse time migration profile of horizontal well with thin interbed model

为探究倾斜井对偏移成像的影响，本文设计了右侧倾斜井和左侧倾斜井两组数值模拟实验，每组实验均包含3个测井倾斜程度变化的数值测试，激发方式为自上而下依次等间隔激发，炮数均为20炮。

为探究右倾程度对成像效果的影响，分别对斜率为0.5、1以及曲斜井进行数值模拟，得到图10a、b、c所示的右倾斜井补偿后偏移剖面。其中图10a为激发井段斜率为0.5的斜井，竖直方向1 000 m，水平方向500 m；图10b为激发井段斜率为1的斜井，竖直方向1 000 m，水平方向1 000 m；图10c为曲斜井，激发井段竖直方向1 300 m，水平方向1 000 m。通过与参考剖面的对比可以看出，当存在右侧倾斜激发井段时，成像范围有一定提升，在深层薄互层处成像范围提升极其明显；通过图10a、b、c的成像剖面对比可以看出，随着激发井段右倾程度增加时，模型右侧的横向探测范围也随之增加，且范围增长明显。

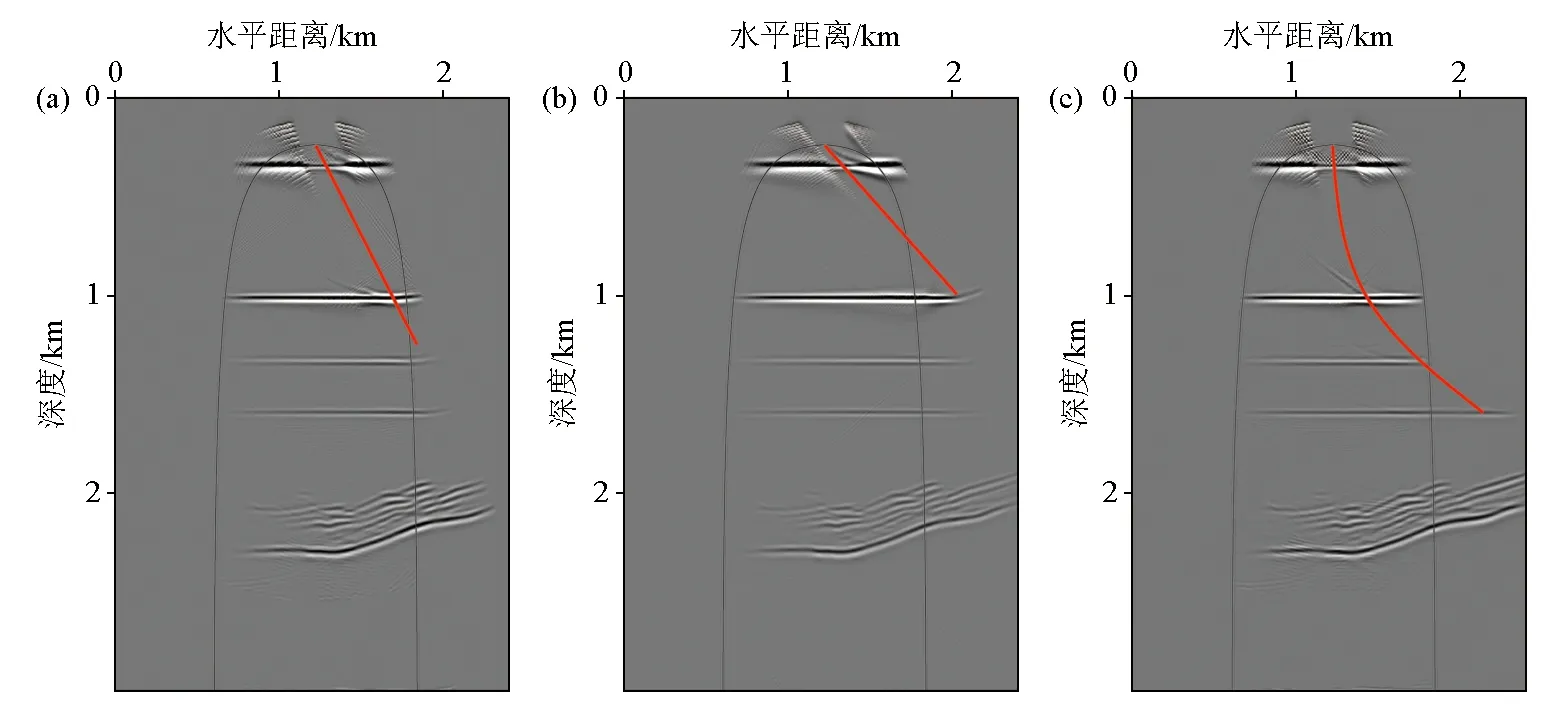
a—斜率为0.5偏移剖面；b—斜率为1偏移剖面；c—右斜井偏移剖面a—offset profile with slope of 0.5；b—offset profile with slope of 1；c—offset profile of right inclined shaft图10 薄互层模型右斜井逆时偏移剖面Fig.10 Reverse time migration profile of right inclined well in thin interbedded model

为探究左倾程度对成像效果的影响，分别对斜率为-0.5、-1以及曲斜井进行数值模拟，得到图11a、b、c所示的左倾斜井补偿后偏移剖面。其中图11a激发井段斜率为-0.5的斜井，竖直方向1 000 m，水平方向500 m；图11b激发井段斜率为-1的斜井，竖直方向1 000 m，水平方向1 000 m；图11c为曲斜井，激发井段竖直方向1 300 m，水平方向1 000 m。将该模型与参考剖面对比可以看出，当存在左侧倾斜激发井段时，成像范围有一定提升，但整体提升不明显；通过图11a、b、c的成像剖面对比可以看出，随着激发井段左倾程度增加时，模型左侧的横向探测范围也随之增加，但范围增长有限。

a—斜率为-0.5偏移剖面；b—斜率为-1偏移剖面；c—左斜井偏移剖面a—offset profile with slope of -0.5；b—offset profile with slope of -1；c—offset profile of left inclined shaft图11 薄互层模型左斜井逆时偏移剖面Fig.11 Reverse time migration profile of left inclined well in thin interbedded model

综合两组倾斜井实验的数值模拟结果，发现斜井激发时相当于在参考井横向上增加了炮点，模型上部分的平层在偏移剖面中成像范围扩大；对模型下部分的薄互层构造成像范围的刻画也有所改变，当激发井段方向与地层倾斜方向相同时，受偏移距的影响，成像范围基本没有变化。当激发井段方向与地层倾斜方向相反时，成像范围扩大明显。

考虑到实际生产中存在的多井联采情况，本文设计双井和三井数值实验，以探究存在多激发井时的偏移成像效果。图12为补偿后的井中地震偏移剖面，激发井段中震源布置方式与图6相同，震源起始深度均为300 m。图12a为双井逆时偏移剖面，两口井分别位于水平方向800 m和1600 m处；图12b为三井逆时偏移剖面，3口井分别位于水平方向600 m、1 200 m和1 800 m处。通过与参考剖面的成像范围对比可见，当进行多井激发时模型整体的横向探测范围有明显扩大；通过双井和三井的偏移剖面对比可见，三井的成像范围明显大于双井，且深层薄互层构造相对清晰。

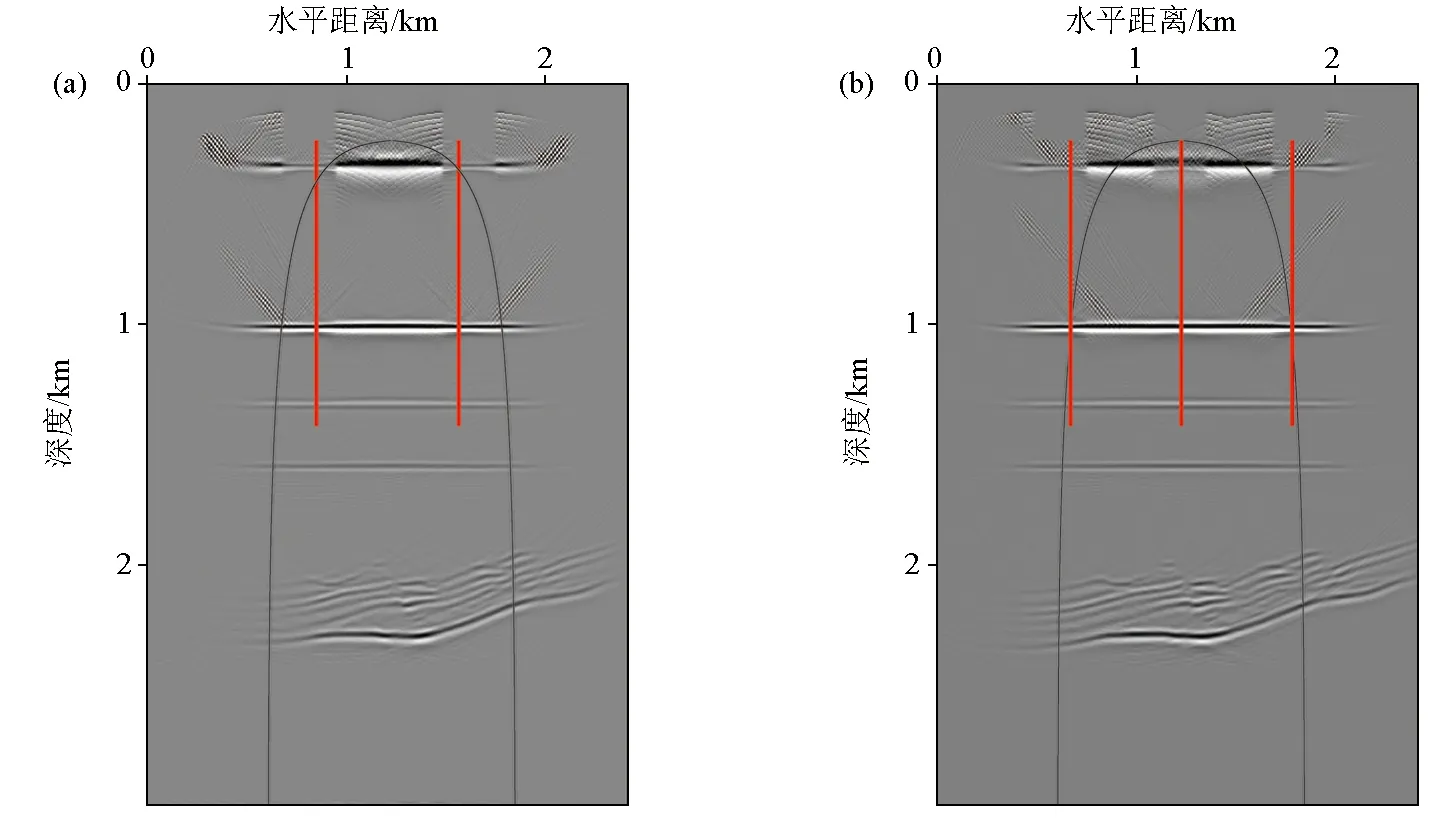
a—双井偏移剖面；b—三井偏移剖面a—double well migration profile；b—mitsui migration profile图12 薄互层模型多井逆时偏移剖面Fig.12 Reverse time migration profile in thin interbed model with multiple wells