基于信息熵的布谷鸟搜索算法

张 燕,袁书卷

(陕西理工大学 教育科学学院,陕西 汉中 723000)

大自然中有一些布谷鸟会将自己的卵产在寄主鸟巢中，将巢寄生作为一种繁殖策略，在某些情况下，寄主鸟类有可能发现鸟巢中陌生的卵，这时寄主鸟类会丢弃布谷鸟所产的卵或直接重新筑巢．从进化的角度来看，布谷鸟的目标是增加生存的概率[1]．受这些行为和策略的启发，Yang和Deb(2009)开发了布谷鸟搜索(CS)算法，布谷鸟搜索算法成功地模仿了布谷鸟的行为，并与Lévy flights相结合，有效地搜索更好、最优的生存策略．由于其具有很强的全局搜索能力，在解决不同的优化问题中表现出了很好的性能，逐渐引起了关注，并被应用到不同的领域，如水电管网系统、资源分配、图像处理、多目标优化等方面[2]．与其他智能算法类似，CS算法也存在搜索速度慢和早熟收敛等缺陷，为了改善CS算法的性能，众多学者针对布谷鸟算法进行了大量的研究．其中王李进[3]等提出逐维改进的布谷鸟搜索算法，改善解的质量．周欢[4]等引入动态惯性权重改进鸟巢位置的更新方式，用于平衡种群探索能力和开发能力之间的关系，改进后的算法收敛速度和收敛精度均有不同程度的提高．薛益鸽[5]基于混沌扰动的改进布谷鸟算法，获得了较快的收敛速度和较高的求解精度．田野[6]等针对布谷鸟搜索算法中解的发现及放弃策略的随机性问题，将解的适应度考虑进来，提出一种基于解的优劣度的改进算法，提高算法的求解质量．本文中针对算法易陷入局部最优和早熟收敛的缺陷，提出了一种 CS算法的改进方法，通过信息熵权重来调控搜索范围，将该权重引入到 CS算法中改善布谷鸟的局部搜索能力，提高收敛速度．

1 基本布谷鸟搜索算法

布谷鸟算法作为一种元启发式算法[7]，其基本原理就是把布谷鸟所寄生的鸟巢位置映射为算法种群空间中的解，与所有进化算法一样，布谷鸟优化算法采用一个随机生成的群体开始迭代搜索．由布谷鸟初始种群(Npop)开始，nesti=(nexti,1,nesti,2,…,nesti,var)代表一个候选解，iE{1,2,…,pop}，var为优化问题的维度，因此，种群空间总体是一个大小为Npop×Nvar的矩阵．以寄生巢位置的优劣作为算法的适应度值，布谷鸟选择寄生巢的过程即为算法寻优的搜索过程，整个过程是局部随机游动和全局探索随机游动的平衡组合．

全局探索采用Lévy飞行执行随机游走，计算如公式(1)：

(1)

其中，nesti(t)表示第t代第i个待更新鸟巢，nesti(t+1)为更新后的下一代鸟巢，α是步长缩放因子，Levy(λ)是莱维随机路径，Levy(λ)～u=t-λ，⊕就是点对点乘积运算．

完成全局探索的Lévy飞行随机游走后，在当前解的基础上，采用偏好随机行走的方式(random walk)，完成局部搜索．根据发现概率Pa与产生的随机数ε比较结果来完成寻优，Pa的取值为0.25[8]，若Pa>ε，则表示鸟巢被发现，即当前解为较差解，按公式(2)更新鸟巢的方向和位置，淘汰较差解，生成新的候选解．鸟巢位置更新公式描述如公式(2)：

(2)

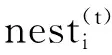
基本CS算法的具体步骤如下:

Step 1.初始化．随机产生N个鸟巢(即问题的解)，记录最优的解；

Step 2.利用莱维飞行进行解的位置更新，获取新的候选解的位置，利用贪心选择策略保留更好的

解；

Step 3.根据发现概率 Pa，丢弃部分解，并用偏好随机游动产生新的解替代丢弃的解；

Step 4.如果满足终止条件，则输出最好的解；否则，返回Step 2继续迭代．

2 改进布谷鸟搜索算法

与其他基于群体智能的启发式算法一样，虽然布谷鸟搜索算法具有很强的全局搜索能力，然而其本身也存在优化精度不高、容易早熟、搜索速度慢等缺陷．本文将信息熵权重引入到基本布谷鸟算法，来调控布谷鸟搜索鸟巢的范围，改善布谷鸟算法的局部搜索能力．

2.1 信息熵

“熵”是德国物理学家克劳修斯(R·Clausius)在 1850 年提出的一个概念，是反映系统微观粒子无序程度的宏观物理量[9]．它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量．1948 年，香农( C·E·Shannon)在 Bell System Technical Journal 上发表了《通信的数学原理》(A Mathematical Theory of Communication)一文，将熵的概引入信息论中，把熵作为一个随机事件的不确定性信息量的量度，称为“信息熵”，按照Shannon的观点，信息熵与系统的有序化程度呈反比，其值随着系统有序化程度的升高而逐渐降低，系统越是有序，信息熵就越低；反之，系统越是混乱，信息熵就越高[10]．

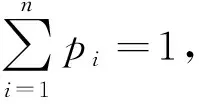
(3)

其中,H(X)代表信息系统的信息熵，Xi是系统中的随机事件，Pi为随机事件的概率．

2.2 信息熵权重计算

在信息论中，信息熵是对系统的有序化程度不确定性的一种度量，可以通过计算熵值来判断一个事件的随机性或系统中某个指标的离散程度，指标的熵值越小，其离散程度越大，该指标对综合评价的影响越大，其赋予的权重就越大[12-13]．现有布谷鸟优化算法生成的一个随机种群

(4)

其中，Nestt表示第t代的种群空间矩阵，由N个个体组成，每个个体包含D个分量，若第j个分量xij～xNj的信息熵值越大，则表示个体间该分量的离散程度越小，取值分布均匀，分量间差异性小，那么在决策过程中该分量影响力就越小，其权重也就越小．相反的，若该分量的信息熵值越小，那么表示选择过程该分量影响力就越大．根据上述分析，信息熵值的大小与分量影响力作用相反，定义种群空间第j个分量的权重为公式(5)：

wj=1-Hj.

(5)

信息熵Hj越大，其赋予的权重Wj越小，影响力越小．

2.3 信息熵加权的布谷鸟算法

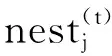
在此，把种群看作是一个系统，根据信息熵值法得到种群中个体分量权重为W= (w1，w2，…，wj)，1≤j≤D，将标准布谷鸟算法的偏好随机游走局部搜索改进为如下公式：

(6)

根据上述改进思路，算法框架如下：

Step 1:设置初始化参数．种群数N，维数D，发现概率Pa和最大迭代次数，随机产生N个鸟巢，记录最优的解；

Step 2:根据公式(1)进行鸟巢的位置更新，获取新的候选解的位置，利用贪心选择策略保留更好的解；

Step 3:根据公式(3)和公式(5)计算信息熵权重w；

Step 4:根据发现概率Pa，丢弃部分解，根据公式(6)更新鸟巢位置，并保留更好的解；

Step 5:若终止条件满足，输出最优值；否则，返回Step 2继续迭代．

3 实验仿真

本次实验在Matlab R2016a版本中，采用8个典型的测试函数进行实验，用以检验本文改进算法的性能．算法初始参数：种群规模N=30，发现概率Pa=0.25，最大迭代次数为1 000，测试函数见表1．

表1 典型测试函数

基本CS算法和改进算法在30维的情况下，每个测试函数被两种算法独立调用30次, 30次运行后结果如表2所示．本文改进算法对F1-F8函数优化结果求解精度均高于CS算法且方差均为0，其中F1-F3、F6、F8找到全局最优解．而对于噪音函数Quartic，虽未达到理论最优结果，但解的精度比CS算法高．综上可以看到，在求解精度方面本文改进算法较基本CS算法具有一定的优势．

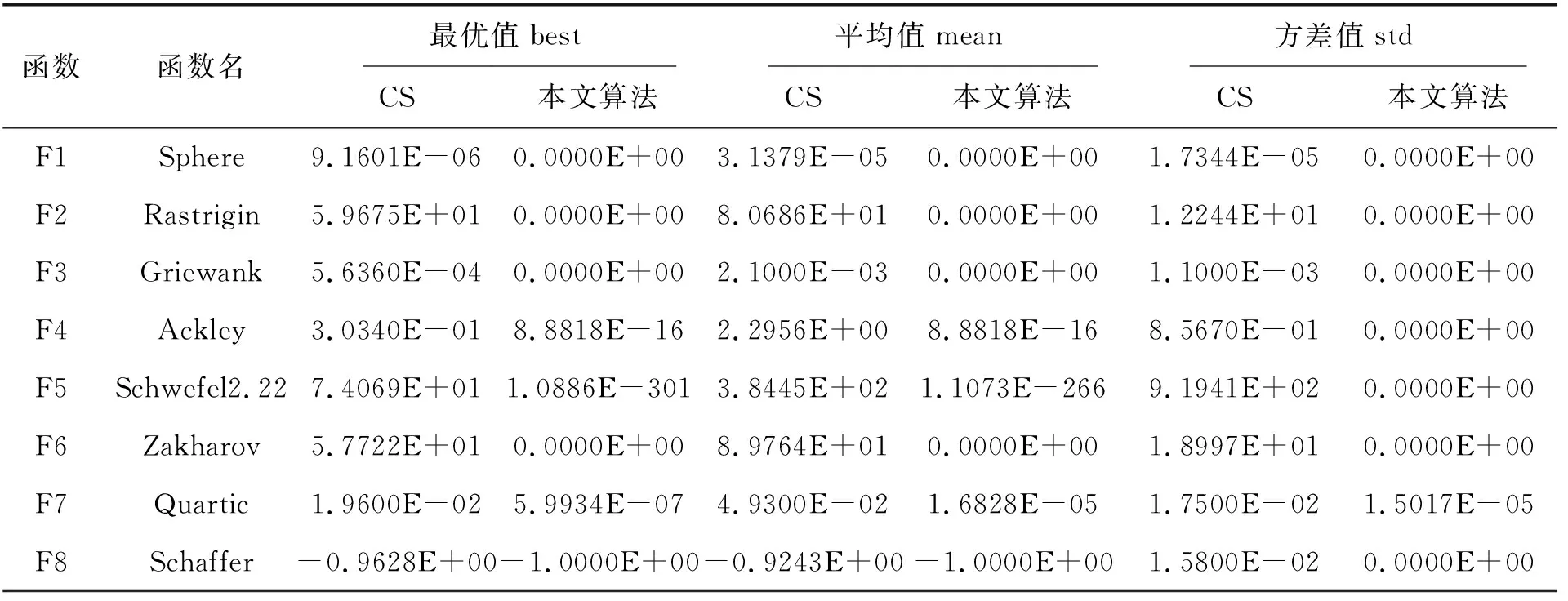
表2 两种算法最优值、平均值和方差

为更进一步验证本文改进算法的性能，选择经典和声搜索算法(HS)、粒子群算法(PSO)、本文改进算法和基本CS算法，对8个测试函数的进化过程进行模拟，进化曲线图如图1中(a)～(h)所示．最大迭代次数1 000.从图中可以观察到(a)-(h)的函数F1-F8利用本文算法均快速收敛，且函数F1-F3、F6和F8收敛至全局最优解．另外，由进化图曲线也反映出CS算法进化过程中缺乏活性，早熟收敛的特性．本文算法收敛速度和寻优精度与其它算法相比较，有显著的改善．

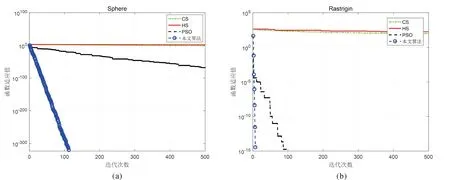
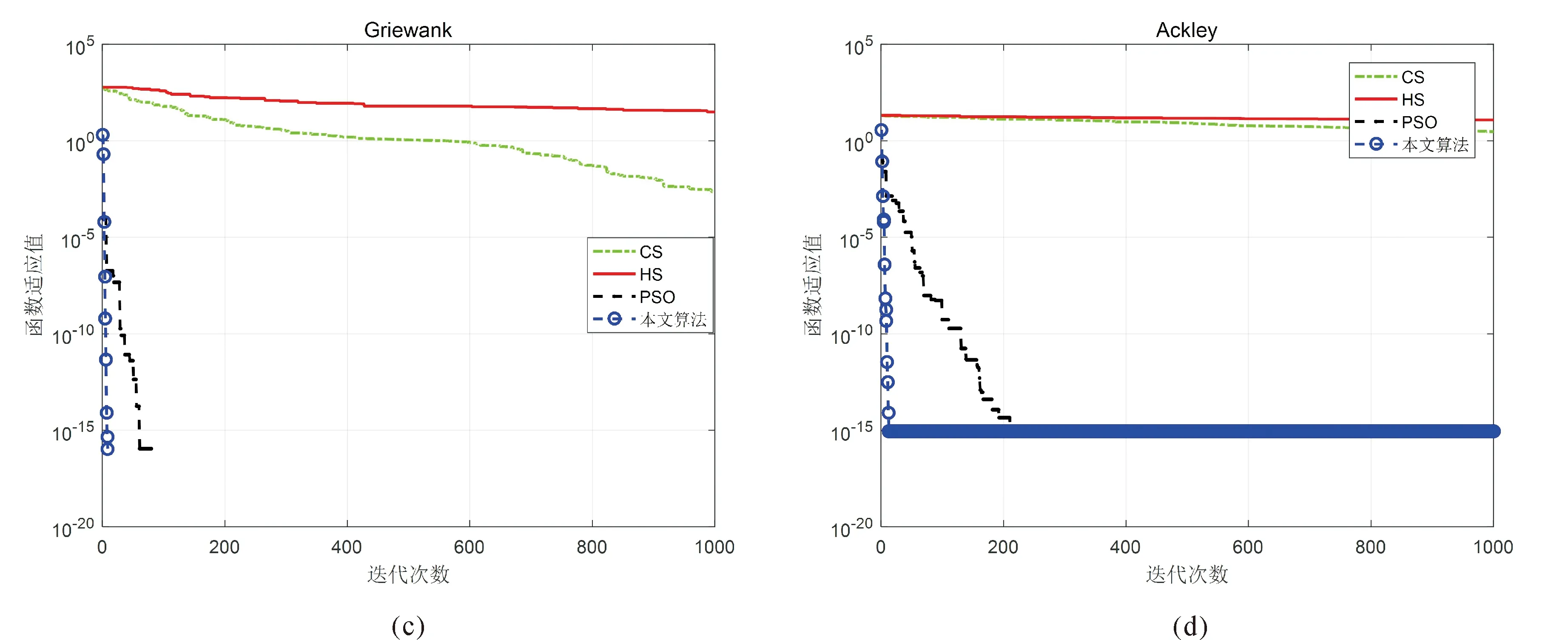
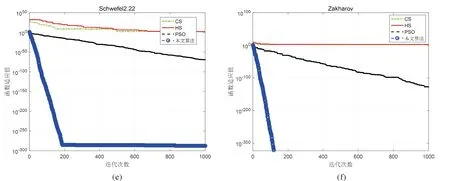
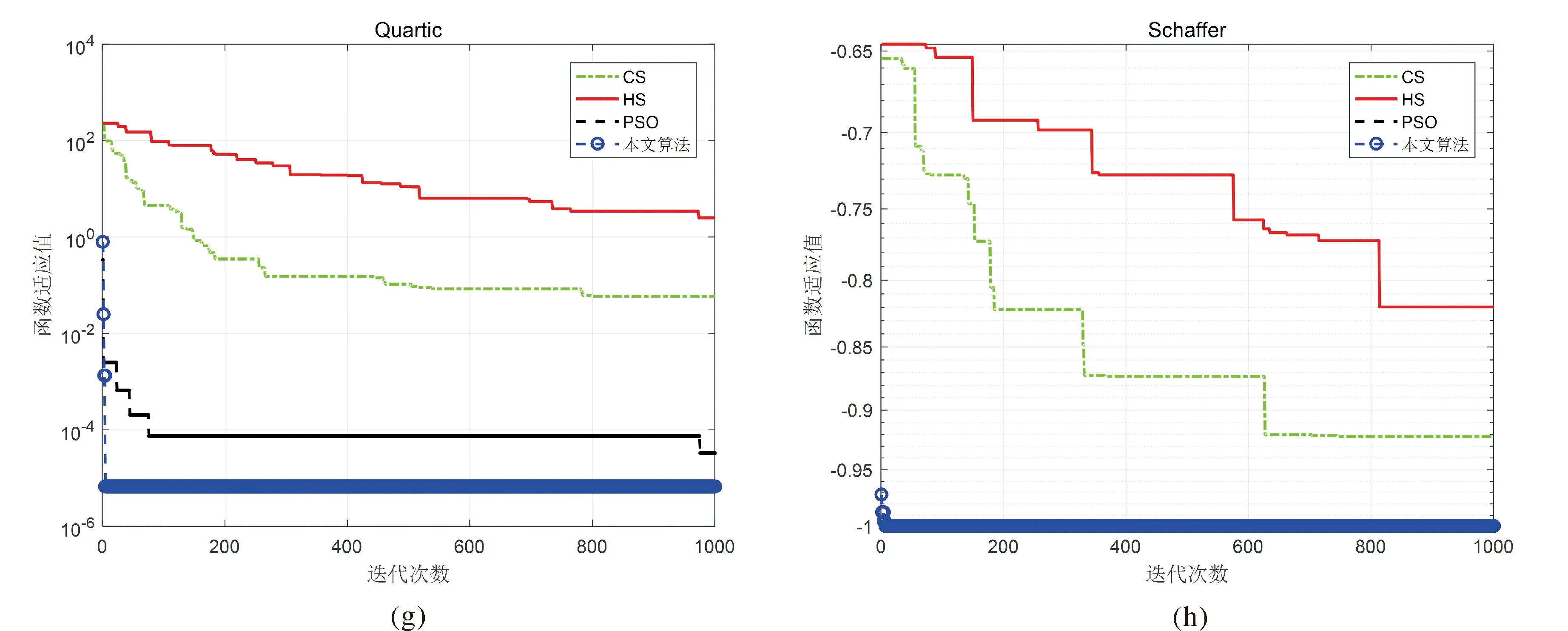
图1 四种算法进化曲线图

4 种群规模对算法执行效率影响分析

本文改进算法把鸟巢种群空间看作是一个系统，根据信息熵值法计算种群个体分量权重为W=(w1，w2，…，wD)，种群规模不同，会影响算法的效率．图2中以F1为测试函数，从种群规模N和维度D两个方面，来检验两者改变对本文算法效率的影响程度．(a)图是算法精度达到1E-300，所完成的迭代次数，实验中当种群数N=30，维数D从5增加到500，需要的迭代次数从260增加到377；当维数D=30，种群数N从5增加到500，迭代次数从312到339，变化幅度较小．(b)图为迭代次数为1 000时，随种群数和维度的变化，消耗的运行时间．当种群数N=30，维数D增加到350维时，运行时间大幅增加；当维度D=30，种群数N改变时，运行时间变化幅度较小．从图2的算法运行效率评价图看出，种群数的增加较之维度的增加，需要更少的迭代次数，消耗更少的运行时间，由此得出问题维数的变化对本文算法效率的影响更大，特别是高维的时候，而种群数的改变影响相对较小．

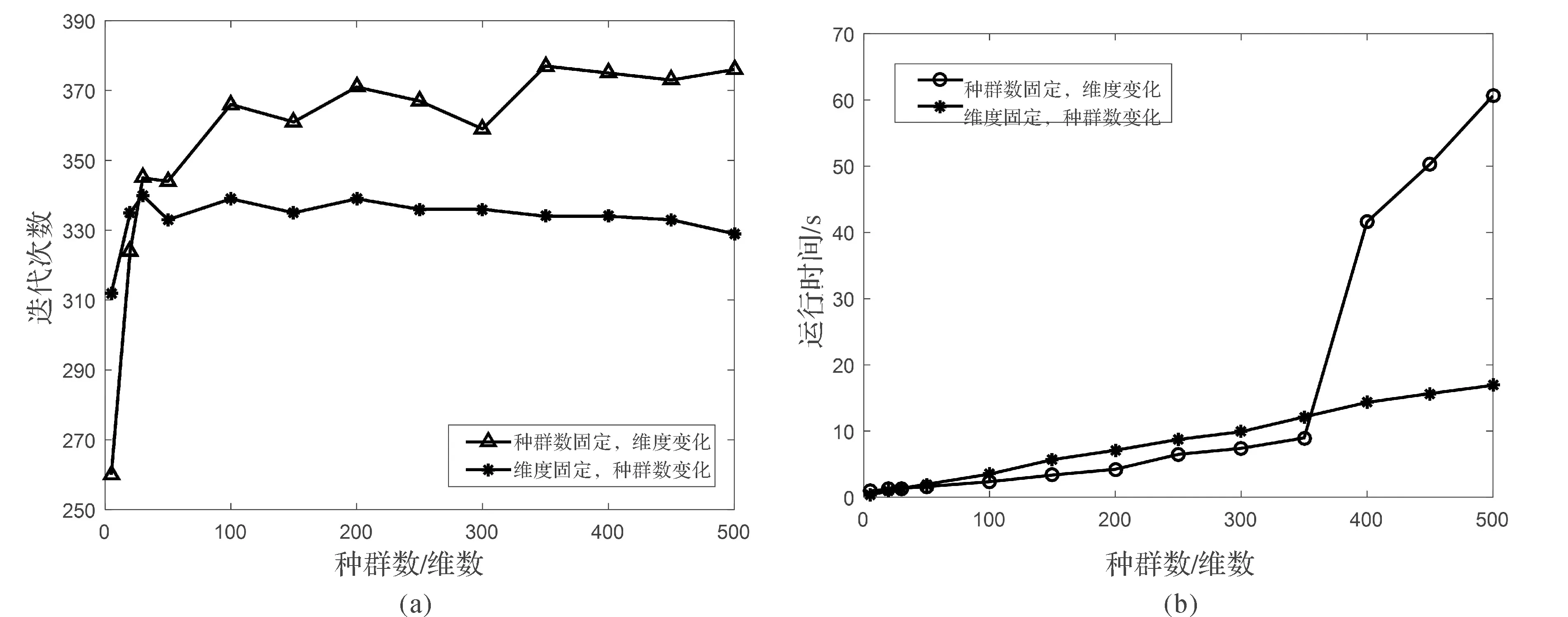
图2 算法运行效率评价图

5 结论

改进后的CS算法克服了寻优过程的完全随机性，在基本CS算法中引入了信息熵权重，用种群中个体分量的信息熵加权来衡量种群中个体的差异程度，并赋予不同的权重，有效避免了算法陷入局部最优和早熟的缺陷，同时算法的求解精度有大幅度提高．仿真实验的模拟和对比分析结果显示，文中提出的改进布谷鸟算法是可行有效的，但在高维运行效率会降低．