面向人工智能物联网的分布式训练通信优化策略

赵晓杰, 陈 晔

(武夷学院 a.信息技术与实验室管理中心、数字福建旅游大数据研究所;b.资产管理处，福建 武夷山 354300)

人工智能物联网是将人工智能技术应用于物联网后诞生的新型网络，能实现更高层次的物联网智能系统[1-3]．人工智能物联网通常由许多传感器和云服务器组成，用于收集、存储和处理数据．同时，随着信息时代的快速发展，对人工智能物联网系统中设备的数据处理和低时延通信提出了更高的要求．但是，由于传感器数量多、体积小、计算能力有限，相互访问和通信的能力有限，需要延长其使用寿命并尽量减少维护次数．因此，如何提高传感器节点之间的通信效率，提高整体的可服务性成为亟待解决的问题之一．为了减少人工智能模型在分布式训练过程中引入的通信开销，将上述问题建模为深度学习中的分布式训练问题[4-5]，提出了一种基于梯度选择策略来降低分布式节点之间的梯度通信传输成本．

1 梯度参数的分布特征

构建了一个由1个嵌入层(word2vec)、1个循环神经网络层、2 个卷积层以及2个全连接层的深度学习模型，并使用TensorFlow提供的TensorBoard工具将训练产生的日志文件可视化，得到如图1所示的梯度分布结果，其中横坐标轴表示梯度值，纵坐标轴表示对应梯度值的统计量．

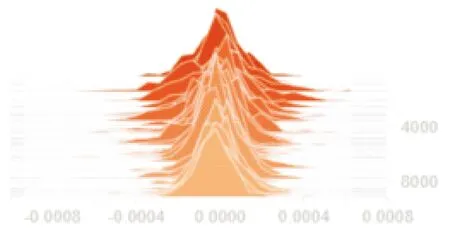
图1 模型的梯度参数分布

综上所述，神经网络中的梯度分布近似于正态分布．根据正态分布的性质可知，大约有68.26%的样本落在(μ-σ,μ+σ)范围之间．这意味着大部分梯度值是分布在0附近(即μ=0)，而这些梯度参数对训练的影响不大．但这些梯度的存在导致了冗余问题．

2 梯度参数的选择策略

2.1 基于阈值划分的梯度选择

将梯度的分布近似为x～N(μ,σ2)．根据梯度更新的特点，选择绝对值较大的梯度值更有利于更新，对权重的影响也较大．因此，将梯度分布的(μ-3σ,μ-σ)∪(μ+σ,μ+3σ)区间作为梯度更新的重点区域，将(μ-σ,μ+σ)区间作为稀疏区域．主要从重点区域中选择梯度值来参与更新，而仅选择少量位于稀疏区域的梯度值参与更新．基于梯度划分，利用信息熵来衡量梯度信息在每个区间的重要性，以此作为梯度选择的依据．

信息熵常用于衡量变量分布的不确定性，离散变量概率分布下的信息熵计算公式为[6]：

(1)

其中，正态分布的概率密度函数为：

(2)

那么正态分布的香农信息的定义为：

(3)

正态分布的信息熵实际上就是香农信息的期望，即：

(4)

由于神经网络中的梯度值都是小数，为保证信息熵为正，将式(4)重写为：

(5)

由式(5)可知，正态分布的信息熵只与其标准差有关．

接下来，提出了一种基于信息熵的梯度阈值筛选算法来设置阈值筛选梯度．该算法的具体过程如算法1所示．

算法1 基于信息熵的梯度筛选算法

输入：梯度集合Gl，∀l∈L

输出：阈值Tl，∀l∈L

1：For l = 1 to L do

3：σl←CompSD();

4：H←CompIE();

6：S=H×γ;

7：Tl=Top-k(Gl,S);

令梯度的阈值为α，那么其对应神经网络层的信息熵为：

(6)

其中，σα是梯度阈值所在神经网络层的标准差．在算法中，γ是用来调整信息熵重要性的权重参数．使用Top-k排序算法来选择前S个最大的梯度，并得到相应的阈值α．

梯度的选择过程可以表示为：

(7)

2.2 梯度传输调度

定义调度效率这一指标来衡量调度的影响和完工时间变化．如果调度期间仅使用了一种资源，相当于调度操作是按顺序进行的，那么此时的完工时间是最长的，即：

U=∑φ∈ΦT(φ)

(8)

其中，T(φ)是调度操作φ所需的时间．调度操作是指从物联网节点向服务器传输梯度．在实践中，物联网节点可以同时向服务器发送梯度，因此真实的完工时间会小于此值U．最短的完工时间可以表示为：

L=maxφ∈ΦT(φ)

(9)

对于给定的迭代，我们测量每个操作的完工时间T(φ)以及该迭代的完工时间m．将调度效率定义为E=(U-m)/(U-L)，并将加速比定义为S=(U-L)/L．该算法的目标是优先考虑那些减少网络通信阻塞的梯度传输，调度算法如算法2所示．将调度操作的通信依赖φ.d定义为与调度操作直接或间接依赖的接收操作集，并采用深度优先图遍历来提取通信依赖关系．调度操作的通信时间是完成该操作所需的总网络传输时间φ.M．

算法2 梯度传输调度算法

输入：调度关系图G，调度操作φ∈Φ，接收操作集合R

输出：调度操作通信时间φ.M，调度操作通信依赖关系φ.d

1：FindDep(G);

2：Forφ∈Φ do

3：φ.M← ∑r∈φ.d∩RT(r);

4：Forφ∈Φ-Rdo

5：D ←φ.d∩ R;

6：If |D| == 1 then

7：Forr∈Ddo

8：r.P ← r.P _ T(φ);

9：If |D| > 1 then

10：Forr∈Ddo

11：r.M ← min {r.M,φ.M}

3 通信优化架构

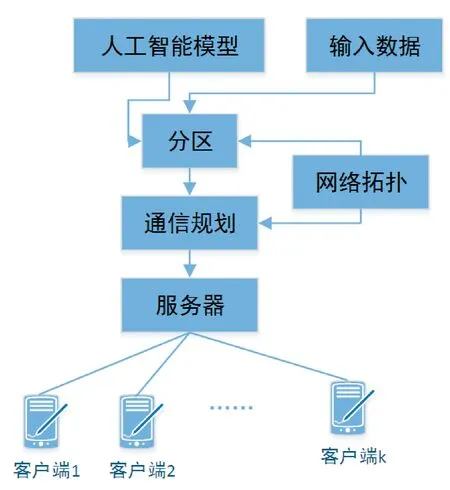
图2 通信优化架构

将通信规划优化问题定义如下：

(10)

Tu是以su为源节点、Du为叶子节点的生成树．将通信计划定义为∪u∈VTu，相应的成本模型为t(∪u∈VTu)．对于每个顶点u∈V，需要找到通信规划Tu(即生成树)．使用最短路径生成树算法进行通信规划，如算法3所示．

算法3 基于生成树的通信规划算法

1：For each u ∈ V do

2：N ← {su }

3：for each i in |Du | do

4：C ← WeightCal();

5：p ← dijkstra(N, D, C)

6：N ← N + p.v

7：S ← S + p.e

4 实验评估

为了验证本策略，搭建了实验仿真环境，模拟神经网络分布式训练场景．本实验使用的数据集为MNIST和Cifar10，训练中使用的神经网络模型为AlexNet和ResNet[7]．模型训练的学习率为0.005．AlexNet在MNIST数据集上的批大小为128，迭代次数为2 000；AlexNet在CIFAR10数据集上的批大小为128，迭代次数为7 000．ResNet在MNIST数据集上的批大小为128，迭代次数为4 500；ResNet在CIFAR10数据集上的批大小为128，迭代次数为9 000．

算法的收敛性是指算法经过多次迭代后，数值趋于某个值，算法的收敛性反映了算法寻找最优解的能力．AlexNet和ResNet网络模型在MNIST和CIFAR10数据集下的准确率分别如表1所示，其中基准算法是指使用所有梯度参与训练的算法．从表1可以看出，提出的策略与基准算法具有相似的准确率．在训练的过程中，虽然早期迭代有一些波动，随着训练步数的增加，曲线的整体波动更加稳定．通过对算法在两种网络模型上的收敛性进行分析，提出的算法在相同的实验条件下都能达到较好的收敛性．

统计了2种网络模型训练中梯度参数的数据量，并计算本策略的参数压缩倍率，结果如表2所示．参数压缩倍率是指模型在训练过程中的梯度数据量与经过本策略压缩后的梯度数据量的比．由表2可以看出，通过在2种不同的网络模型上进行测试，算法的压缩率随着网络层数的增加而增加．在AlexNet模型中，本算法可以达到29.3倍左右的压缩率，而对于层数较多的网络模型ResNet，可以达到37.2倍左右的压缩率．

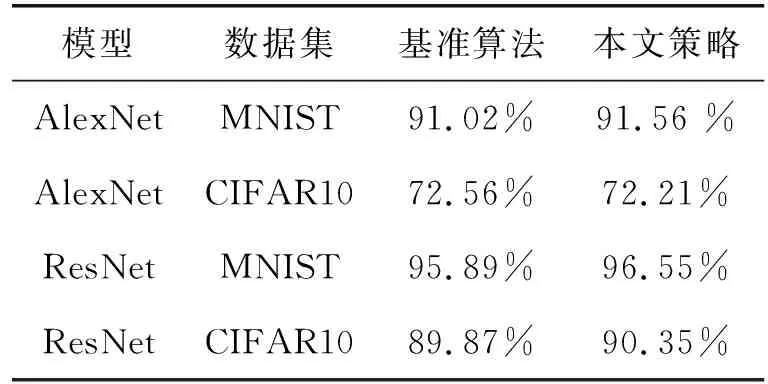
表1 模型训练准确性

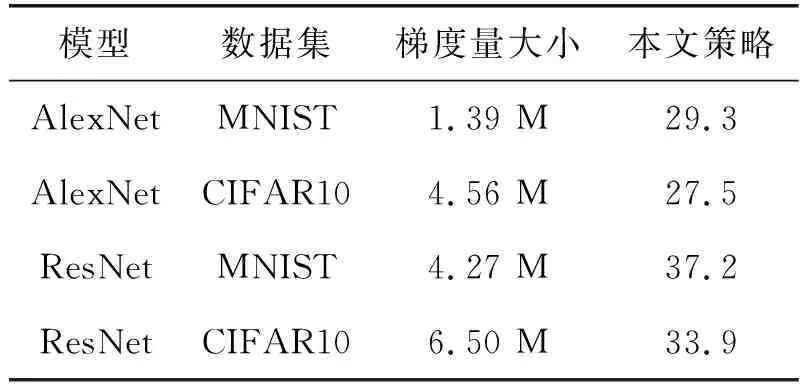
表2 梯度参数压缩倍率

5 结论

本研究提出了一种基于阈值划分的梯度压缩策略，以优化分布式训练的通信过程．该策略根据梯度的分布特征，通过阈值选择参与训练的梯度值．通过分析可知，该策略在不同的神经网络模型训练后都能达到正常收敛，在一定程度上减少了梯度参数的传输量，并保证了训练精度和收敛性.该策略能为人工智能物联网的理论和应用的优化提供有用的思路．