一种采用NFV架构的服务功能链动态编排与部署*

吴宇彤， 周金和

(北京信息科技大学 信息与通信工程学院， 北京 100101)

0 引 言

在传统网络中，网络功能由不同的硬件设备提供，网络服务提供商(Network Service Provider,NSP) 需要在用户请求新服务时部署大量新设备，价格昂贵且灵活性差，加大了资本支出和运营费用。为解决上述问题，软件定义网络/网络功能虚拟化技术应运而生。软件定义网络(Software Defined Networking,SDN) 技术通过解耦控制平面和用户平面以实现集中控制，加强网络的灵活性。网络功能虚拟化(Network Function Virtualization,NFV) 架构使网络功能从硬件中抽象出来并能在虚拟机上运行。NSP提供的服务通常是通过服务功能链(Service Function Chaining,SFC) 来实现的。SFC是指引导流量按序通过一组虚拟网络功能(Virtual Network Function,VNF)以提供端到端服务的过程。

近年来，关于SFC部署的研究已成为一个热门话题。但现有研究仅关注静态SFC编排，未考虑服务请求的动态变化[1-2]；或者未考虑SFC与新型网络技术的结合[3-5]，如SRv6技术；或者仅考虑一个或两个优化目标，没有考虑动态SFC部署的多目标优化[5-6]。

目前部署 SFC 的一个关键问题是如何在保证提供服务的同时降低端到端时延、资源消耗和负载压力。为应对以上挑战，本文首先引入在 NFV架构下的SFC动态部署问题，然后将SFC部署与SRv6机制相结合，设计SFC动态编排(SFC Dynamic Orchestration,SFCDO) 算法。算法包括两步：第一步选用广度优先搜索(Breadth-first Search,BFS) 算法遍历物理网络并找到可部署SFC的最短路径；第二步选择启发式的蚁群优化算法(Ant Colony Optimization,ACO) 得到最佳且可动态调整的SFC部署方案。

与现有文献相比，本文考虑的SFC部署是动态的，同时采用SRv6技术，结合NFV架构对SFC进行编排和部署。并且本文提出的SFCDO算法在考虑网络负载均衡的同时，可以有效降低用户到NSP的延迟和服务传输的带宽资源消耗，是对SFC部署的多目标联合优化。该方案可以应用于网络功能的编排，为用户提供高效及时的各类服务。

1 系统架构

本文采用的NFV架构如图1所示。

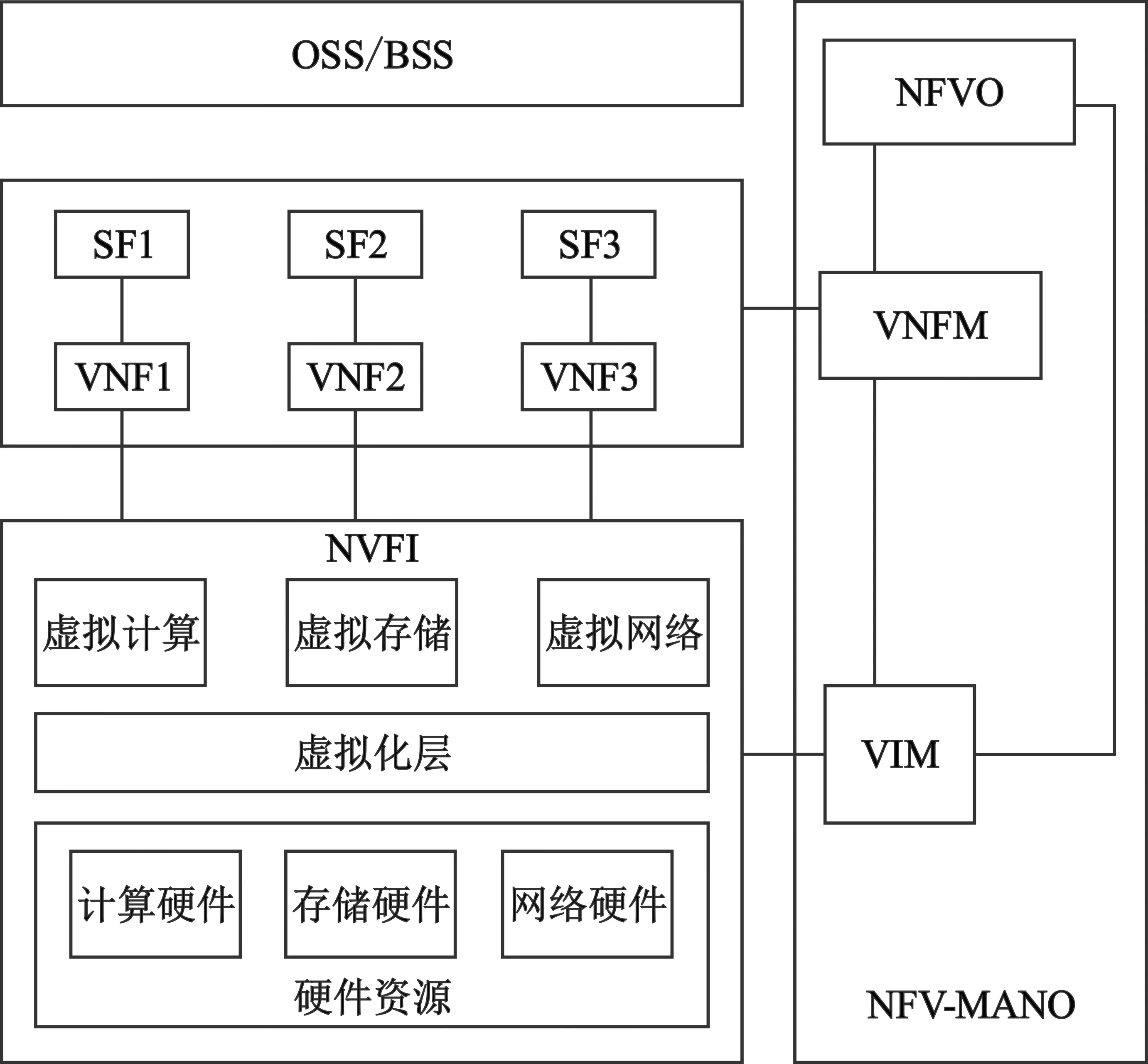
图1 ETSI NFV架构图

NFV编排器(NFV Orchestration,NFVO) 用于管理 VNF 操作，例如实例化、删除和扩展VIM。VNF管理器(VNF Manager,VNFM) 负责管理VNF实例。在传统NFV架构中，网络全局视图中流量的转发规则由SDN控制器提供。在这个架构中，由于结合SRv6技术，所以使用SR控制器来发送段标签。根据源路由机制，控制器只需将所有信息统一发送到源节点即可。这一操作可减轻控制器负载，其他节点不需要维护每个流的状态。3GPP中对网络功能进行了定义，每个网络功能(Network Function，NF)可提供不同服务。本文中假设一个NF提供一个特定服务，架构中可用VNF来表示NF。

接下来将说明基于 NFV架构的SFC编排，如图2所示。在域中，一个NFV节点托管多个VNF。与VNF相关的数据包在入口节点中被分类。根据一个SFC的指示，流将依次通过不同VNF。

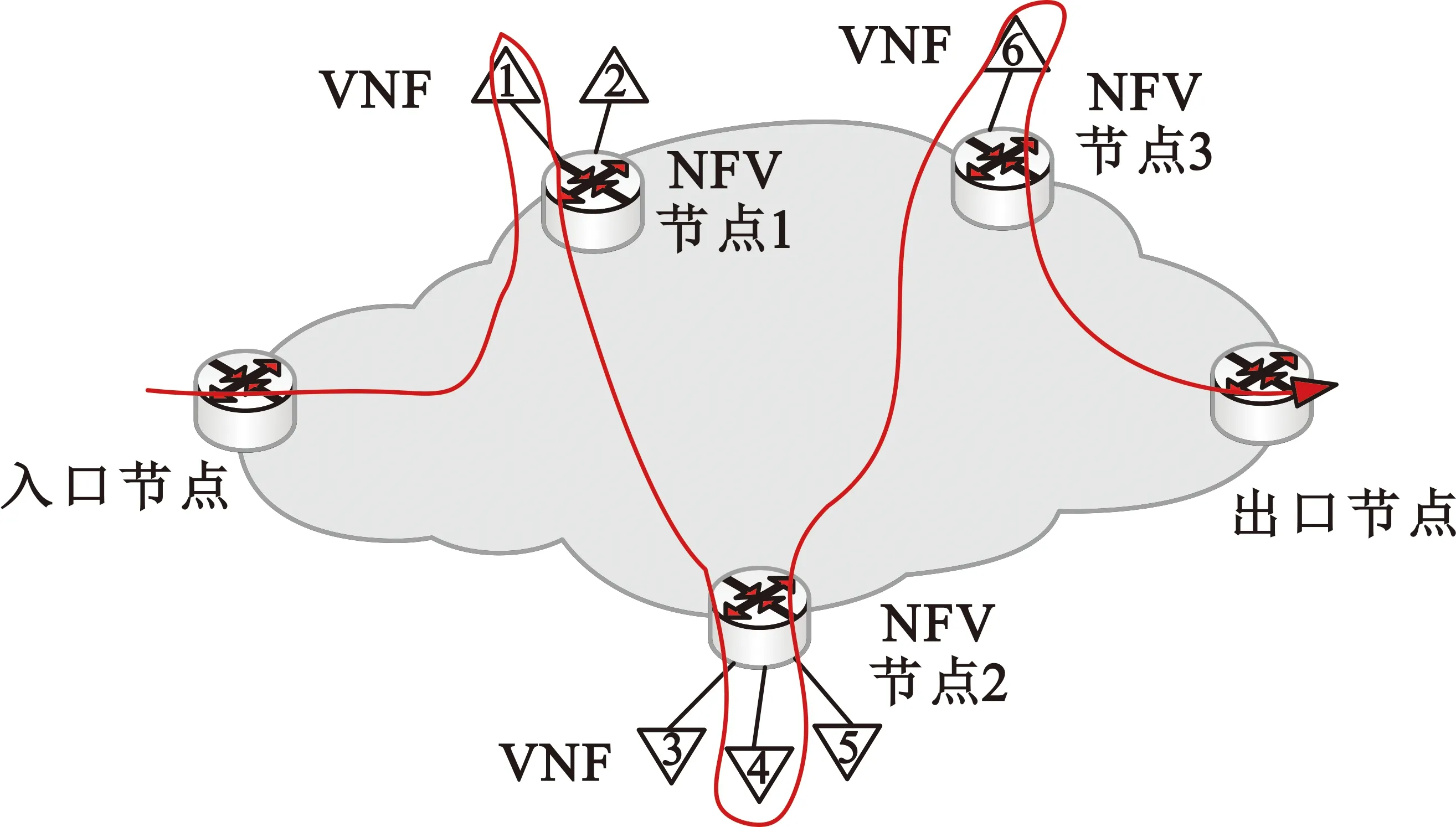
图2 基于NFV的SFC编排示意图

图3描述了数据包在SRv6机制下的传输过程和过程中报文的变化。数据包首先通过分类器Head，再在段标签指引下依次通过SFC中的每个VNF(VNF1→VNF4→VNF6) 。数据包中封装有 IPv6 标头和包含分段列表的 SRH。

图3 SRH工作流示意图

2 问题描述与建模

2.1 物理网络

首先，本文采用一个无向图G=(V,E)来表示底层物理网络，其中，V={v1,v2,v3,…,v|M|}表示物理节点集合，E={e1,e2,e3,…,e|N|}表示物理链接集合，物理节点和物理链接的总数分别为|M|和|N|。节点负载率L(vi)由公式(1)进行计算：

(1)

式中：vi表示一个物理节点，其具有一定的计算资源，可用c(vi)表示;r(vi)表示剩余计算资源。

一个物理链接ei也可表示为一个节点对，如公式(2)所示，其中eiva和eivb代表链接ei两端的节点。

ei=(eiva,eivb),∀ei∈E。

(2)

b(ei)表示物理链路上的带宽资源，剩余带宽资源用r(ei)表示，链路负载率L(ei)用公式(3)进行计算：

(3)

p(vi,vj)表示从节点vi到节点vj的一条路径，由公式(4)可知，p(vi,vj)中包含该路径上所有物理链接。

p(vi,vj)={em,…,en}⊆E,∀vi,vj∈V。

(4)

D[p(vi,vj)]表示路径p(vi,vj)的端到端时延，这一参数包括dprop、dproc和dtrans三个部分，如公式(5)所示。其中，dprop指的是传播时延，因为本文不考虑跨域部署SFC，因此设dprop为0；dproc表示数据包处理时延，为固定值，可不予考虑，故端到端时延等同于传输时延dtrans，由公式(6)进行计算。

D[p(vi,vj)]=dprop+dproc+dtrans，

(5)

D[p(vi,vj)]=∑ek∈p(vi,vj)d(ek),∀vi,vj∈V。

(6)

以上是对物理网络的参数建模，接下来对SFC请求中的参数进行定义。

2.2 SFC请求

一个SFC请求可定义为SFC=(VS,ES,S,D,F)。其中，VS={vnf1,vnf2,vnf3,…,vnf|VS|}表示SFC中所有VNF的集合，ES={vl1,vl2,vl3,…,vl|ES|}表示SFC中所有虚拟链接的集合，|VS|和|ES|分别表示VNF和虚拟链接的数量，S和D分别是SFC的起始节点和目的节点，F是经过该SFC的有序流。

一个VNF所需的计算资源为c(vnfi)，V(vnfi)表示部署vnfi的物理节点。假设一个二元变量M(vnfi,vj)，若vnfi成功部署在节点vj上，则M(vnfi,vj)=1；反之,M(vnfi,vj)=0。以上过程由公式(7)定义：

M(vnfi,vj)∈{0,1},∀vnfi∈VS,∀vj∈V。

(7)

b(vli)表示部署一个虚拟链接vli所需的带宽资源。一个虚拟链接可表示为一对VNF，由公式(8)可知，vlivnfa和vlivnfb分别是虚拟链接vli两端的VNF。

vli=(vlivnfa,vlivnfb),∀vli∈ES。

(8)

同样地，定义另一个二元变量N(vli,ej)来描述虚拟链接的部署情况。如果N(vli,ej)=1，说明虚拟链接vli成功部署在物理链接ej上；反之，则N(vli,ej)=0。以上过程由公式(9)表示：

N(vli,ej)∈{0,1},∀vli∈ES,∀ej∈E。

(9)

p(vli)表示部署虚拟链接vli的物理链接，E(vli)表示vli部署的路径，D(vli)表示vli的延时,B(vli)表示vli部署路径的带宽资源消耗。公式(10)～(12)分别定义以上变量，其中NUM[E(vli)]是指路径E(vli)上的链接数量。

E(vli)=p[V(vlivnfa),V(vlivnfb)],∀vli∈ES，

(10)

D(vli)=d[E(vli)]=∑ek∈E(vli)d(ek),∀vli∈ES，

(11)

B(vli)=b[E(vli)]=b(vli)×NUM[E(vli)]。

(12)

2.3 动态SFC部署

SFC中的源节点S和目的节点D分别代表网络服务提供商和用户的位置。除此之外，标准文件RFC7665中定义SFC是有序的， 因此在公式(13)中用F表示这种有序的流。

(13)

在部署过程中，Ta(SFCi)代表当前SFC和上一个SFC之间的到达时间间隔，Fs(SFCi)代表当前SFC的服务时间，TR(SFCi)代表响应一个SFC所需的时间。DL(SFCi)代表一个SFC的端到端时延，BW(SFCi)代表部署它所需的带宽资源，分别由公式(14)和(15)计算。

DL(SFCi)=∑vlk∈ESD(vlk),∀SFCi∈SSFC，

(14)

BW(SFCi)=∑vlk∈ESB(vlk),∀SFCi∈SSFC。

(15)

SFC部署情况可用二元变量P(SFCi)来描述：如果SFC部署成功，则P(SFCi)=1；反之，P(SFCi)=0。以上过程由公式(16)表示：

P(SFCi)∈{0,1},∀SFCi∈SSFC。

(16)

在一个完整的SFC部署过程中，所有的SFC请求用SSFC={SFC1,SFC2,SFC3,…,SFC|SSFC|}代表，其中|SSFC|是请求总数。NUMsuss(SSFC)代表SFC成功部署的数量，DLall(SSFC)代表总延时，BWall(SSFC)代表总带宽消耗，TR(SFCi)代表响应一个SFC所需的时间，TRall(SSFC)代表SSFC总响应时间，分别由公式(17)～(20)计算，本文仅考虑成功部署的情况。

NUMsuss(SSFC)=∑SFCk∈SSFCP(SFCk)，

(17)

DLall(SSFC)=∑SFCk∈SSFCDL(SFCk)×P(SFCk)，

(18)

BWall(SSFC)=∑SFCk∈SSFCBW(SFCk)×P(SFCk)，

(19)

TRall(SSFC)=∑SFCk∈SSFCTR(SFCk)×P(SFCk)。

(20)

SFC的动态编排需考虑服务请求的到达和离开。部署过程中，Ta(SFCi)代表当前SFC和上一个SFC之间的到达时间间隔，Fs(SFCi)代表当前SFC的服务时间。一个服务请求的动态到达和离开都遵循泊松分布，因此，SFC到达时间间隔和服务时间这两个参数独立同分布，均遵循指数分布，计算公式如(21)和(22)所示。

(21)

(22)

同时在部署过程中，LB(SFCi)表示物理网络的负载率，由公式(23)可知，它由节点负载率和链路负载率共同决定，其中α是权重因子。

LB(SFCi)=α×L(vi)+(1-α)×L(ei)。

(23)

2.4 网络资源约束

当虚拟网络功能vnfi部署到物理网络节点V(vnfi)上时，需要确保vnfi所需计算资源应小于物理节点剩余计算资源r[V(vnfi)]，且物理节点消耗的总计算资源应小于其自身固有计算资源。以上约束由公式(24)和(25)定义：

r[V(vnfi)]≥c(vnfi),∀vnfi∈V；

(24)

c(vj)≥∑SFCk∈SSFC∑vnfi∈VSM(vnfi,vj)×c(vnfi),∀vj∈V。

(25)

在SFC部署过程中，每个VNF只能映射到一个物理节点上，两者是一对一映射的关系。这样可以简化SFC部署方案，避免出现VNF集中部署在某个节点的情况，更好实现负载平衡。以上过程约束由公式(26)、(27)给出：

0≤∑vj∈VM(vnfi,vj)≤1,∀vnfi∈VS；

(26)

0≤∑vnfi∈VSM(vnfi,vj)≤1,∀vj∈V。

(27)

对于一个虚拟链接vli和它所在的物理部署路径E(vli)，需确保vli的带宽消耗小于物理路径E(vli)的剩余带宽r[E(vli)]。物理链接ej消耗的总带宽需小于自身固有带宽资源，同时，一个物理链接ej仅能部署一个虚拟链接vli。以上约束由公式(28)～(30)表示：

r[E(vli)]≥b(vli),∀vli∈ES;

(28)

b(ej)≥∑SFCk∈SSFC∑vli∈ESN(vli,ej)×b(vli),∀ej∈E；

(29)

0≤∑vli∈ESN(vli,ej)≤1,∀ej∈E。

(30)

3 算法设计

3.1 广度优先搜索算法

首先使用BFS算法(算法1)寻找源节点S和目的节点D间的最短物理路径。NSP和用户分别位于源点和目的节点上，BFS利用序列遍历查找最短路径的长度，执行步骤如下：

输入:物理网络G=(V,E)；源节点S；目的节点D。

输出:最短路径的长度;最短路径的拓扑信息。

初始化:queue=∅,

将节点S加入队列queue;

while queue≠∅,do

将下一个节点加入list1;

标记S为已查询;

将S加入list2;

hop=hop+1;

ifD在队列queue中,do

将所有节点加入list2;

清空list1;

length=hop

return length 和 path

end if

end while

算法1的输入是物理网络拓扑信息。邻接表用于存储网络中节点和链接的位置信息。SFC请求的起始节点和结束节点已知，该算法输出起始节点和目标节点间最短路径的长度。

首先执行初始化操作。变量queue用于进行网络遍历和路径查找。queue遵循先进先出原则，在开始时置为空。此外设置一些用于记录的参数。queue是当前到达节点，list1记录待检查节点，list2记录已检查节点，hop记录到达该节点时的路径长度，path记录当前节点的路径拓扑信息，length是节点S和D之间的最短路径长度。

BFS的输出结果将作为SFC 部署的基础信息。VNF 和虚拟链路会分别部署在物理网络最短路径的节点和链接上。

3.2 蚁群优化算法

本文使用ACO算法来得到最佳的SFC动态部署方案。

ACO依赖于信息素浓度初值，这会导致局部最优解。因此，本文采用遗传算法(Genetic Algorithm,GA)获取信息素浓度初值。基于GA的交叉变异因子，可改进信息素浓度设置，增强传统ACO的全局搜索能力。

具体做法是：在算法的早期阶段，使用 GA 来初始化种群，因为它具有较快的初始收敛速度，所以很容易得到更好的解。接下来，将这个较好的解作为ACO的初始信息素输入，然后运行ACO算法。因为采用GA进行预处理，不易陷入局部最优，得到的最优解更接近实际的最优解。

蚁群优化算法(算法2)中，蚂蚁数量用m表示，所有节点之间的信息素用矩阵P表示，Bestlength表示最短路径，Bestscheme表示最佳部署路径；Tabu是一张存放所有已访问节点的表，Allowed是存储未访问节点的表；Matrix Delta存储一个循环中的信息素信息；整个路径的开销用 Tourlength表示。假设算法运行次数为 NUM，总运行次数为MAX_GEN，运行时间为t。算法流程如下：

输入:物理网络G=(V,E)；源节点S；目的节点D。

输出:最佳部署路径Bestscheme。

初始化:t=0,Bestlength→∞,Besttour=0,Delta=0,Tabu=0,Allowed=0

for 每一条链路 do

设置从遗传算法中得到的信息素初值p;

end for

将所有节点添加到表 Allowed中;

for 每只蚂蚁kdo

随机选择初始起点；

将源节点S加入表Tabu;

在表 Allowed中删除节点S;

由公式(31)寻找下一节点T;

将T加入表Tabu;

在表 Allowed中删除节点T；

end for

由公式(32)计算启发式因子Delta;

计算Tourlength的值;

if Tourlength < Bestlength then

Bestlength = Tourlength;

Besttour = Tabu;

else

continue;

end if

NUM=NUM+1;

t=t+nt;

由公式(33)更新矩阵P;

if NUM=MAX_GEN then

return Besttour;

else

再次初始化；

end

蚂蚁从起点S出发，下一个节点的选择概率由公式(31)计算，启发式因子由式(32)计算。

(31)

(32)

公式(31)中，τij(t)代表节点i和j在时间t的信息素浓度，α和β分别代表信息素浓度和启发因子的权重；ηij代表从节点i到j的可见度，是两节点距离dij的倒数，由公式(32)可知，dij越小，ηij越大。信息素矩阵由公式(33)进行计算和更新，τij(t+n)代表时间t+n时节点i和j的信息素浓度。公式(34)中Δτijk代表蚂蚁k在节点i和j间留下的信息素。公式(35)中Q表示一个正常数，Lk代表蚂蚁在一次迭代中遍历的路径距离，即Tourlength。

τij(t+n)=(1-ρ)·τij(t)+Δτij，

(33)

(34)

(35)

3.3 算法复杂度分析与对比

本文提出的算法分为两步，下面分别分析其复杂度。

在广度优先算法中，假设底层物理网络有m个节点和n个链接。每个节点最多只能进出一个队列一次，因此操作队列的总时间为O(m)。网络拓扑信息存储在邻接表中，BFS只在节点弹出队列时扫描邻接表，每个顶点的邻接表最多扫描一次，因此扫描邻接表的总时间是O(n)。故算法1的时间复杂度为O(m+n)。

在蚁群优化算法中，假设蚂蚁数量有k只，底层物理网络的节点有m个，则通过对算法各步骤的分析可得到算法2的复杂度为O(m2+m)[7]。

因此，本文所提SFCDO算法的复杂度为O(m2)。本文算法与可靠性保证算法(Ensure Reliability，ER)[8]、基于负载均衡的可靠性保证算法(Ensure Reliability Cost Saving, ER_CS)[8]和贪婪-模拟退火算法(Greedy-Simulated Annealing, G-SA)[6]的复杂度对比如表1所示。

表1 复杂度对比

4 仿真与结果分析

本节通过模拟仿真试验验证本文算法的性能,并将其与现有ER[8]、ER-CS[8]和G-SA[6]三种算法进行对比。

4.1 实验参数设置

本文使用Java搭建仿真环境，仿真网络使用Intel i7 4.0 GHz CPU、9.8 GB RAM的主机，采用GT-ITM的Waxman 2 拓扑模型， 随机生成不同尺寸的网络实例用于SFC部署。在实验所用物理网络中，设定小拓扑网络含有50个节点，大拓扑网络有200 个节点。综合考虑SFC的部署成本和时间，使用Intel i7 CPU实现两种拓扑网络。

参照文献[9]中的实验参数设置，本文设置的实验参数见表2。

表2 仿真参数

本文选择的优化目标包括平均端到端时延、平均带宽资源消耗、最大节点负载率、最大链路负载率和部署成功率。

4.2 实验结果分析

4.2.1 平均端到端时延

如图4和图5所示，随着SFC长度增加，四种算法产生的平均端到端时延随之增加。一般来说，对于SFCDO和其他三种对比算法，时延的增长速度与底层物理链路的增长速度几乎相同。

图4 小拓扑中的平均端到端时延

图5 大拓扑中的平均端到端时延

在两种拓扑中，SFCDO 的端到端延迟均小于对比算法， 原因是本文所提算法倾向于跳数更少的最短路径，因此可以有效减少链路传输时延。仿真结果表明，与对比算法相比，SFCDO算法在小拓扑和大拓扑中的端到端时延分别平均减少了24%和20%。

4.2.2 平均带宽资源消耗

平均带宽资源消耗的仿真结果如图6和图7所示。在两种拓扑结构中，随着SFC长度增加，带宽消耗相应增加。SFCDO的带宽消耗总是小于其他算法，这是由于在选择部署虚拟链接的物理链路时，本文所用BFS算法会选择链接更少的路径，因此部署消耗带宽相应减少。在小拓扑和大拓扑中，这一参数分别平均优化21%和15%。

图6 小拓扑中的平均带宽资源消耗

图7 大拓扑中的平均带宽资源消耗

4.2.3 最大节点负载率

图8和图9展示了两种拓扑中的最大节点负载率。最大节点负载率随SFC长度增加而增长，但SFCDO中的节点负载率总是低于其他三种算法。两种拓扑中的曲线走势有所不同：在图8小拓扑网络中，四条曲线相距很近，但当SFC长度大于6时，三种对比算法的节点负载率都有下降，因为SFC长度大于6时，对比算法的部署成功率下降，它们的节点负载率也相应受到影响。同时，SFCDO节点负载率始终低于对比算法，说明该算法可以有效避免节点拥塞。在图9中，SFCDO的曲线始终低于对比算法。当SFC长度增加时，对比算法的最大节点负载率几乎达到1，但SFCDO这一参数的值总是低于0.6，说明在大拓扑中，启发式蚁群算法可以根据之前的部署情况调整部署方案，所以节点负载率始终保持在较低水平。

图8 小拓扑中的最大节点负载率

图9 大拓扑中的最大节点负载率

4.2.4 最大链路负载率

图10和图11展示了两种拓扑中最大链路负载率的仿真结果。最大链路负载率会随着SFC长度增加而增长， 总体上其他三种算法的曲线总是高于本文算法，大拓扑中结果更加明显。因为在本文算法中，使用蚁群算法部署VNF时会倾向于部署在负载率更低的节点上，相应地，经过这些节点的链路负载率也就更低。对比算法中，VNF总是部署在中心节点上，经过的链路负载也高，因此它们的节点负载率和链路负载率均大于SFCDO算法。

图10 小拓扑中的最大链路负载率

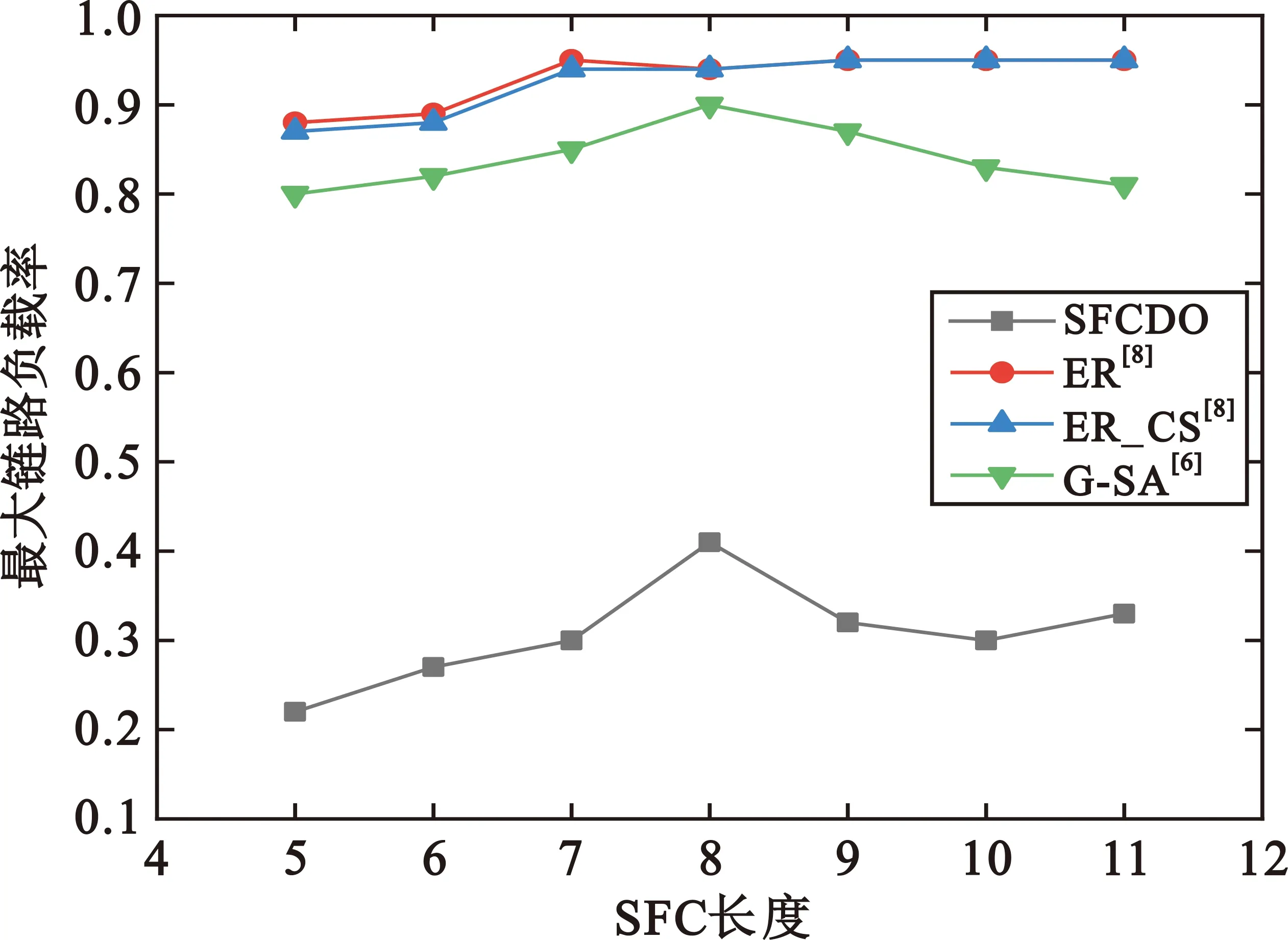
图11 大拓扑中的最大链路负载率

4.2.5 部署成功率

图12和图13展示了在两种不同拓扑中SFC的部署成功率。在两种拓扑网络中，SFCDO算法的成功率均保持在95%以上，并且不会随着SFC长度的增加而降低。由前文可知，本算法较好地提升了网络负载，极少出现部署过载的中心节点，因此部署成功率相对较高且稳定。然而在对比算法中，随着SFC长度的增加，部署成功率会逐渐下降。在两种拓扑结构中，SFCDO算法平均优化部署成功率23%。

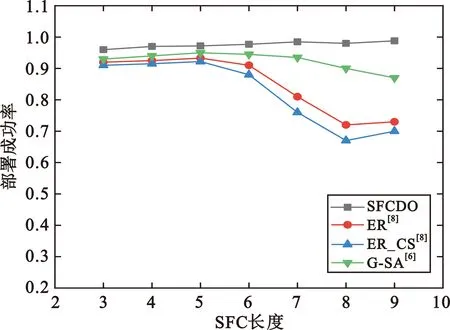
图12 小拓扑的部署成功率

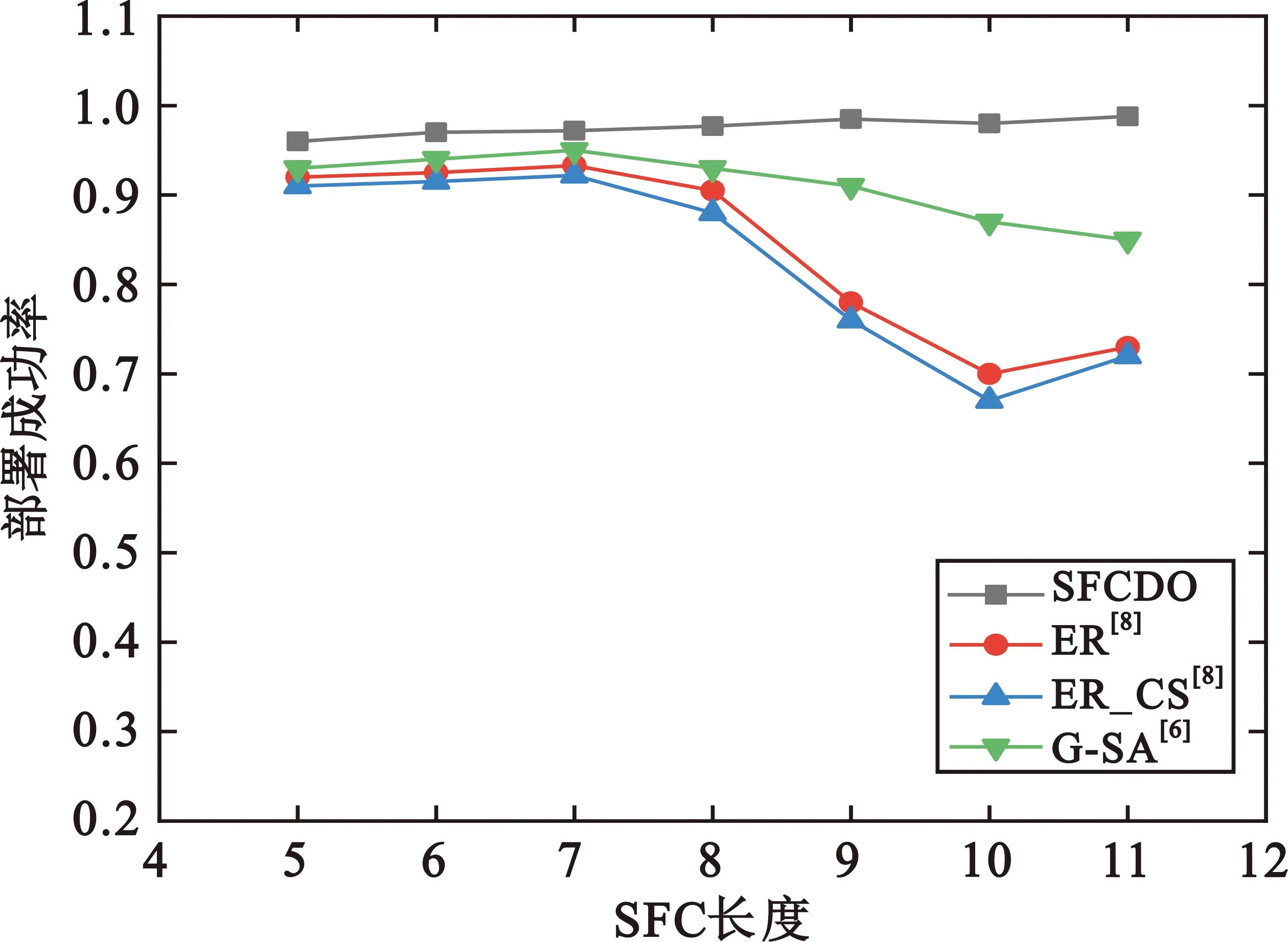
图13 大拓扑的部署成功率

5 结束语

本文考虑基于NFV的SFC动态编排和部署问题，首先提出可用于SFC编排的NFV架构，然后描述结合SRv6机制的SFC编排原理和工作流程，提出SFCDO算法用于提升部署过程的性能，包括端到端时延、带宽资源消耗和负载均衡。仿真结果表明，本文算法在端到端时延、带宽资源消耗和负载均衡方面均有所优化，本文部署方案具有一定优化效果。

在未来SFC部署问题的研究中，由于5G、6G、基于意图的网络等新型网络通信架构的出现和应用，可进一步考虑将机器学习、深度学习等先进技术融入到SFC部署问题中。同时，5G异构网络中的资源调度也值得深入研究，高效的异构网络切换方案对于用户QoS的提升和SFC服务提供也具有启发意义。未来，我们将尝试利用深度强化学习技术实现用户意图的转化，并将其与SFC部署问题相结合，优化其在新网络架构下的整体性能。