基于圆形阵列的OAM波束产生系统设计与实现*

许 强，谢跃雷，2

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.卫星导航定位与位置服务国家地方联合工程研究中心，广西 桂林 541004)

0 引 言

近些年来，携带轨道角动量(Orbital Angular Momentum，OAM)的电磁波以其能有效增加无线信道容量和提高频谱利用率的优势受到了广泛关注。根据Maxwell方程理论，电磁波既可传输能量，也可传输动量，电磁波的动量可分为线动量和角动量，而角动量又可分为自旋角动量(Spin Angular Momentum，SAM)和轨道角动量[1]。自旋角动量与电磁波的极化有关，轨道角动量相位波前围绕着波束轴旋转，形成螺旋形结构，故携带OAM的电磁波又称为涡旋电磁波。理论上讲，涡旋电磁波具有无穷种OAM模态，且不同模态之间相互正交，利用不同模态的涡旋电磁波进行数据传输，可以极大地提高通信容量，且信息之间不会互相干扰[2-4]。另外因其特殊的螺旋相位结构，对目标探测的回波中可能提供更多、更准确的信息，涡旋电磁波信号的产生是其应用的前提和关键。

目前产生涡旋电磁波的方法主要有螺旋天线[5-7]、抛物面天线[8]、环形行波天线[9]、超表面材料天线[10-11]、天线阵列[12-13]五种。其中，文献[6]的螺旋天线是一根导线和匹配负载组成，导线呈圆柱形螺旋结构；文献[7]中螺旋天线是通过在方位角上上升一个平面，从而产生相位差得到涡旋电磁波：两者对上升的高度和位置要求较高，且只能产生固定OAM波束，模态单一。文献[8]是一个非平面的螺旋结构，抛物面天线通过反射入射电磁波来产生相位差，该方法和螺旋天线类似，也只能产生单一模态数的涡旋电磁波；文献[9]通过谐振腔内的谐振模式辐射来产生OAM波束，虽可产生多模态OAM波束，但都为固定模态，无法实现多模态可调。文献[10-11]中的超表面材料天线是近些年刚提出的一种方法，通过旋转结构单元，理论上能对电磁波相位进行灵活调控，但其制作成本高，调控难度大，还处于探索阶段。文献[12-13]中的天线阵列为圆形阵列，通过对阵列中的各个阵元施加等幅度、等相位差的激励信号，从而产生OAM波束。除此之外，天线阵列还有矩形阵列、密度加权阵列两种形式。天线阵列可通过调节相位差来产生任意模态数的涡旋电磁波，其OAM波束的设计和实现具有很好的可行性。

本文采用圆形阵列的方法，设计并实现了一种中心频率为10 GHz的电磁涡旋微带贴片天线，利用HFSS和feko电磁仿真软件对天线结构进行建模仿真、参数优化，确定参数后进行加工制作，搭建实验系统平台，对产生的涡旋电磁波进行模态测量。实测结果表明，在考虑误差的情况下，该阵列天线能产生纯度较高的涡旋电磁波，与螺旋天线、抛物面天线方式相比，可灵活调控产生不同模态的OAM波束，具有很好的可重用性；与环形行波天线、超表面天线方式相比，具有低成本、低复杂度等优点。在实际应用当中，本设计天线由于其体积小，易组装拆卸，可随意更换测试场地，调节相位产生不同模态的OAM波束，可获得不同模态下的目标回波信号，从而反演出更多目标特征信息。

1 均匀圆形阵列天线模型

采用均匀圆形阵列天线可以产生模态可控、纯度较高的涡旋电磁波，其天线模型如图1所示[14]。设阵元数为N，天线阵元在xoy平面上均匀排列为一个圆，圆的半径为a，以坐标原点为参考点，第n个天线的方位角为φn。

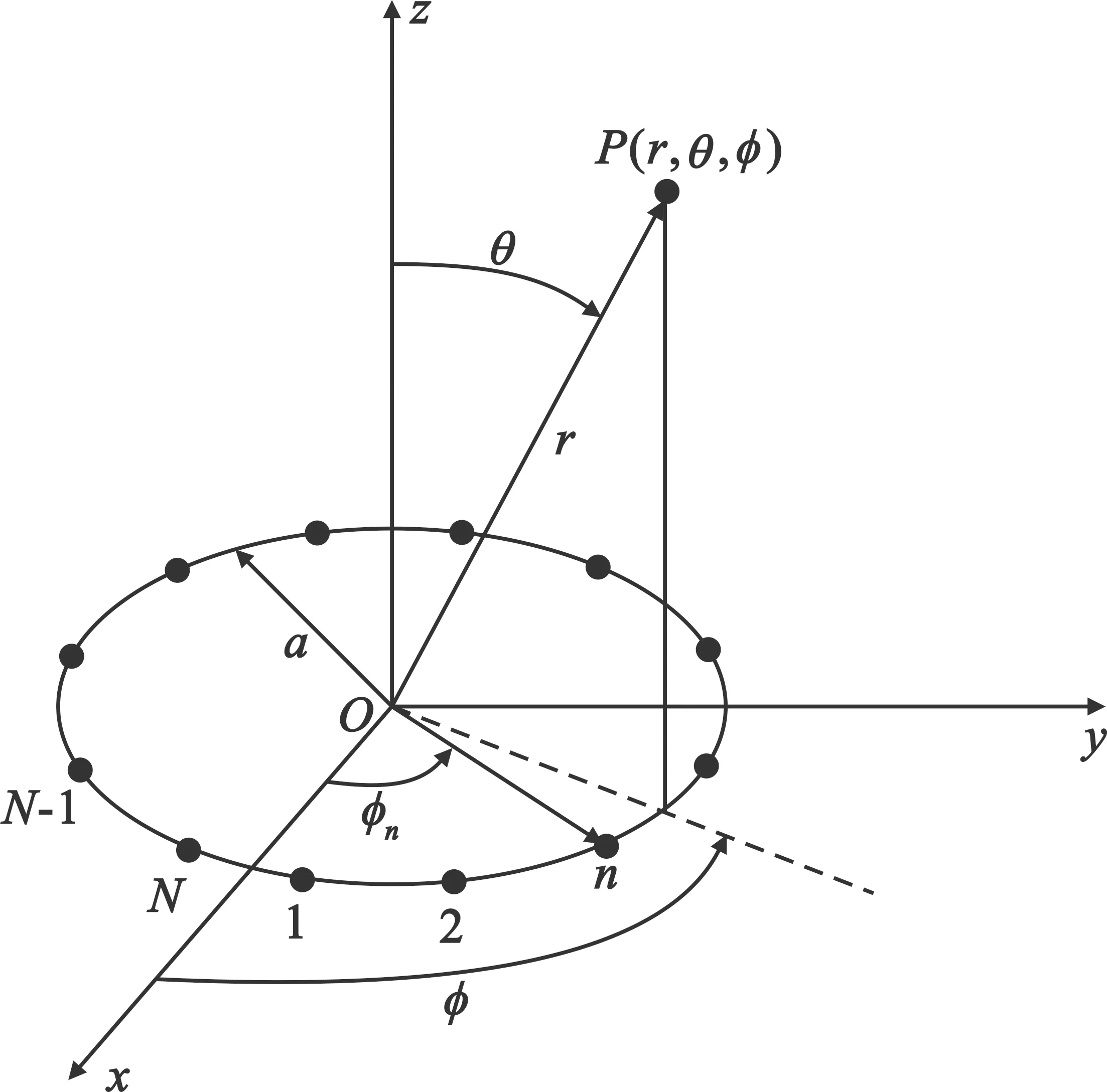
图1 均匀圆形阵列天线模型

假设天线单元为各向同性天线，空间中有一任意观测点P(r,θ,φ)，其中，r表示观测点到原点的直线距离，θ为P点对应的倾斜角，φ为P点对应的方位角，则空间中任意点P处的辐射场En(r)可以表示为

(1)

对各阵元施加幅度相同，相位等间隔递增的激励信号，相邻两个阵元激励相位差为Δφ=2πl/N(l为轨道角动量模态数),故式(1)可变为

(2)

式中：φn=2π(n-1)/N,n=1,2,…,N；Bn为第n个天线单元激励信号幅度值，一般各天线的幅度相同；k表示波矢量。

由代数几何可以得到

|r-rn|=r-asinθcos(φ-φn)。

(3)

将式(3)带入到式(2)中得

(4)

对于远场观测点而言，一般r>a，则假定r>>asinθcos(φ-φn)，式(4)化简为

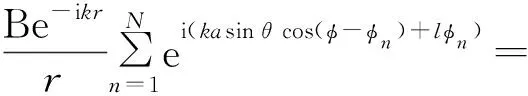
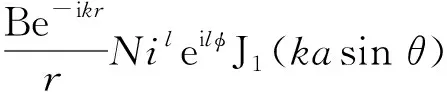
(5)

式中：eilφ是与空间方位角相关的旋转相位因子，包含涡旋电磁波的OAM信息；J1(kasinθ)为第一类贝塞尔函数。根据式(5)的数学模型，利用Matlab仿真，天线阵元设为400个，频率为10 GHz，天线单元激励信号幅值为1 W，相邻阵元相位差为π/200，阵列半径为10λ，观测距离1 000λ，观测窗口大小100λ×100λ，OAM为+1，得到涡旋电磁波的幅度和相位分布图如图2所示。

(a)幅度分布

由图2(a)可知，幅度中心处和最外圈处的能量较低，而圆环处能量较高，类似“甜甜圈”的结构。图2(b)的相位一圈变化360°，且相位波前呈螺旋结构，与涡旋电磁波的幅度和相位特性一致吻合，故均匀圆周阵列能有效地产生涡旋电磁波。

2 均匀圆阵列天线结构设计

考虑阵元天线在空间中的辐射更加均匀，采用微带天线作为阵元，不仅可以产生较高纯度的OAM波束，还使其整个天线结构简单小巧，更利于实验室进行测量和实验。除此之外，微带天线具有低成本、易制作等优点，被广泛应用于雷达、微波射频以及卫星导航系统等多个领域。

图3(a)所示为微带天线阵元的设计结构图，采用矩形结构设计，主要由介质基片、辐射贴片、参考地组成。将8个阵元均匀排列在圆形介质基板上，各阵元之间夹角为45°，其天线结构如图3(b)所示。介质基板材料采用TLY-5，相对介电常数εr为2.2，损耗正切为0.000 9，介质基片厚度h为1.6 mm，中心工作频率为10 GHz。 为了防止天线阵元之间的耦合效应，每个阵元之间的间距保持在0.6～0.8个波长之间，阵元天线的中心到圆心的距离为45 mm，圆半径为60 mm。

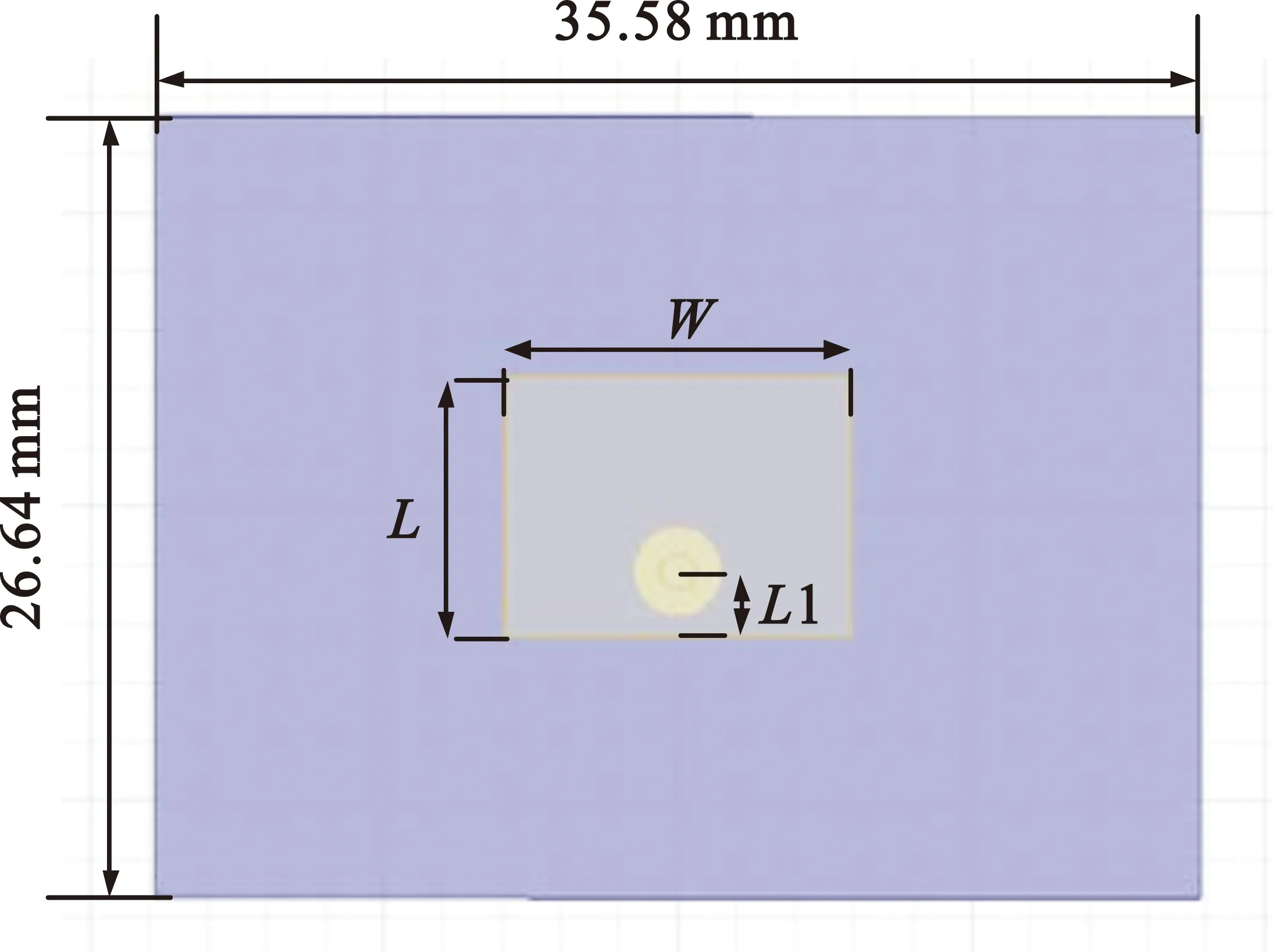
(a)微带天线阵元结构图

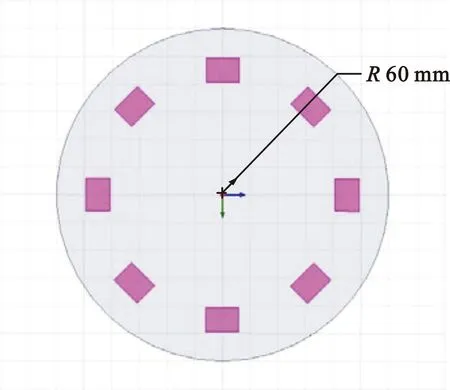
(b)8阵列天线结构图图3 均匀圆阵天线结构示意图

根据微带天线理论公式[15]计算可得到天线阵元尺寸的相关参数，如表1所示。

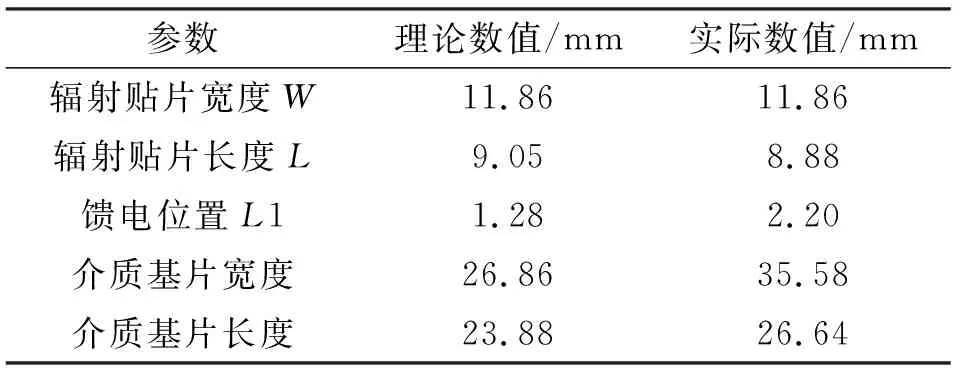
表1 微带天线阵元参数

表1中，理论数值为公式计算得到的初步值，而实际数值是利用电磁仿真软件HFSS进行仿真，调整相关参数，使其在10 GHz工作频率处回波损耗达到最小，且能够达到很好的阻抗匹配，得到调整之后的尺寸。

天线阵元的数量N决定该天线所能产生的模态数lOAM的数量，即满足

(6)

阵元数目越多，产生的模态数种类就越多。本文采用8阵元结构，同轴馈电方式，输入阵元信号的幅度一致，相位依次增加，即可产生不同模态数的涡旋电磁波，阵元之间的相位差Δφ与模态数的关系如下所示：

Δφ=2πlOAM/N。

(7)

3 仿真结果分析

利用电磁仿真软件HFSS对天线进行仿真，其回波损耗和阻抗匹配如图4所示。图4(a)为阵列天线的回波损耗，中心频点10 GHz处的S11值约为-51.5 dB，-10 dB带宽约为0.9 GHz，由此可见信号在天线中的传输效率高。从图4(b)Smith圆图中可以看出，在中心频率处能达到很好的阻抗匹配。

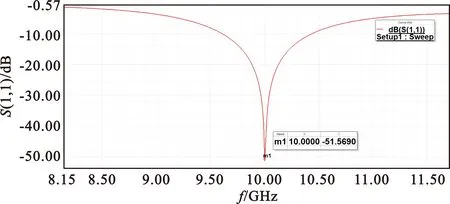
(a)回波损耗

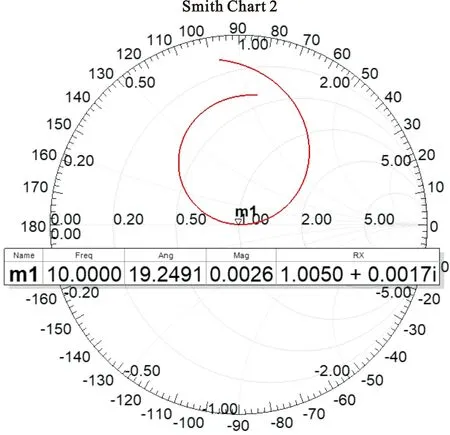
(b)Smith圆图图4 阵列天线的回波损耗和Smith圆图

对阵元天线输入激励信号，各阵元之间幅度相同，均为1 W，相位差分别为0°，45°，90°，135°时，相应产生模态数为0，+1，+2，+3的OAM波如图5所示，图中的观测面位于圆形阵列天线正上方100 mm，半径为120 mm，模态数的正负决定相位波前的螺旋方向，考虑篇幅，本文只给出了正模态数的电场幅度和相位分布。

图5(a)各阵元之间的相位差为0°，即没有相位差，其表示平面波，由于涡旋电磁波模态数相互正交，可线性叠加，也可称为OAM=0的涡旋电磁波，其相位分布呈现出一个个圆环，这与平面波的波前相位一致。

从图5(b)～(d)的幅度分布图可以看出，其幅度中心处能量比周围少，呈现出中空现象，且随着模态数的增加，中空区域的面积越大，这说明模态数越大，其能量越发散。通过相位分布图可以明显看出，相位的螺旋分支数和OAM的模态数是一致对应的，轨道角动量模态数越大，相位分布的分支数越多，波前扭曲程度越复杂，而相位分布图连续性不高主要是由于仿真的阵元个数导致，当阵元数足够多，如图2所示，其分布图连续性高，而阵元个数导致的不连续性会对模态的纯度造成影响，但模态纯度能保持在90%以上。因此，仿真结果表明本文的圆形阵列天线能产生良好的、多模态的涡旋电磁波。

图5 各模态的幅度和相位分布

不同模态数的涡旋电磁波的辐射方向也有一定影响，其E面辐射方向图关于θ=0°完全对称，当模态数增加，其主瓣指向角也变大，说明在模态数较高时，其电磁波能量较发散，而模态数越低，其电磁波能量越集中。

4 实验测试结果与误差分析

为了验证圆形阵列天线的可行性，对该天线进行加工制作，图6(a)为圆形阵列天线实物，图6(b)为圆形阵列天线产生涡旋电磁波的收发系统，该系统主要由矢量网络分析仪、功分器、移相器、圆形阵列天线、同轴线组成。收发天线之间的距离为10个波长，即300 mm，由于实物的中心频率为9.97 GHz，故矢网仪发射频率设为9.97 GHz。由于实验条件有限，实验采用四阵元作为发射天线，功分器将一路信号分为4路，保证各路信号幅度一致，移相器调节每路信号相位，使其相位差为90°，通过同轴线连接到发射天线，理论能产生+1模态数的涡旋电磁波。接收天线采用均匀圆周采样，采样点数为8，收发天线的中心点保持在同一水平线上，这样能够尽量保证天线无偏轴接收。为尽量减小噪声的干扰，整个实验环境在微波暗室中进行。

图6 实测系统

对采样得到的8路幅度和相位信息进行Matlab处理，由于存在噪声干扰，故先对信号进行滤波处理，即先对相位信号进行均值，原始信号与均值差大于45°，则视为噪声或不相关点进行剔除，剩下的点则保留不变。由于幅度信号受噪声干扰较小，经滤波处理后基本和原始信号一致，故只给出相位滤波前后图对比。如图7所示，(a)表示8组相位数据，其中蓝色表示原始采样信号，红色表示滤波之后的信号；(b)表示采样一周时相位的变化；(c)表示采样一周时幅度的变化。从图7(a)中可看出，经滤波处理之后，每组相位信号较为平稳。对滤波之后的每组信号平均化，得到一周之内幅度和相位的变化如图7(b)、(c)所示，可见采样一周后相位几乎变化360°，且相位为由负到正逐步增加，而幅度基本不变，与模态数为+1的涡旋电磁波特征一致。

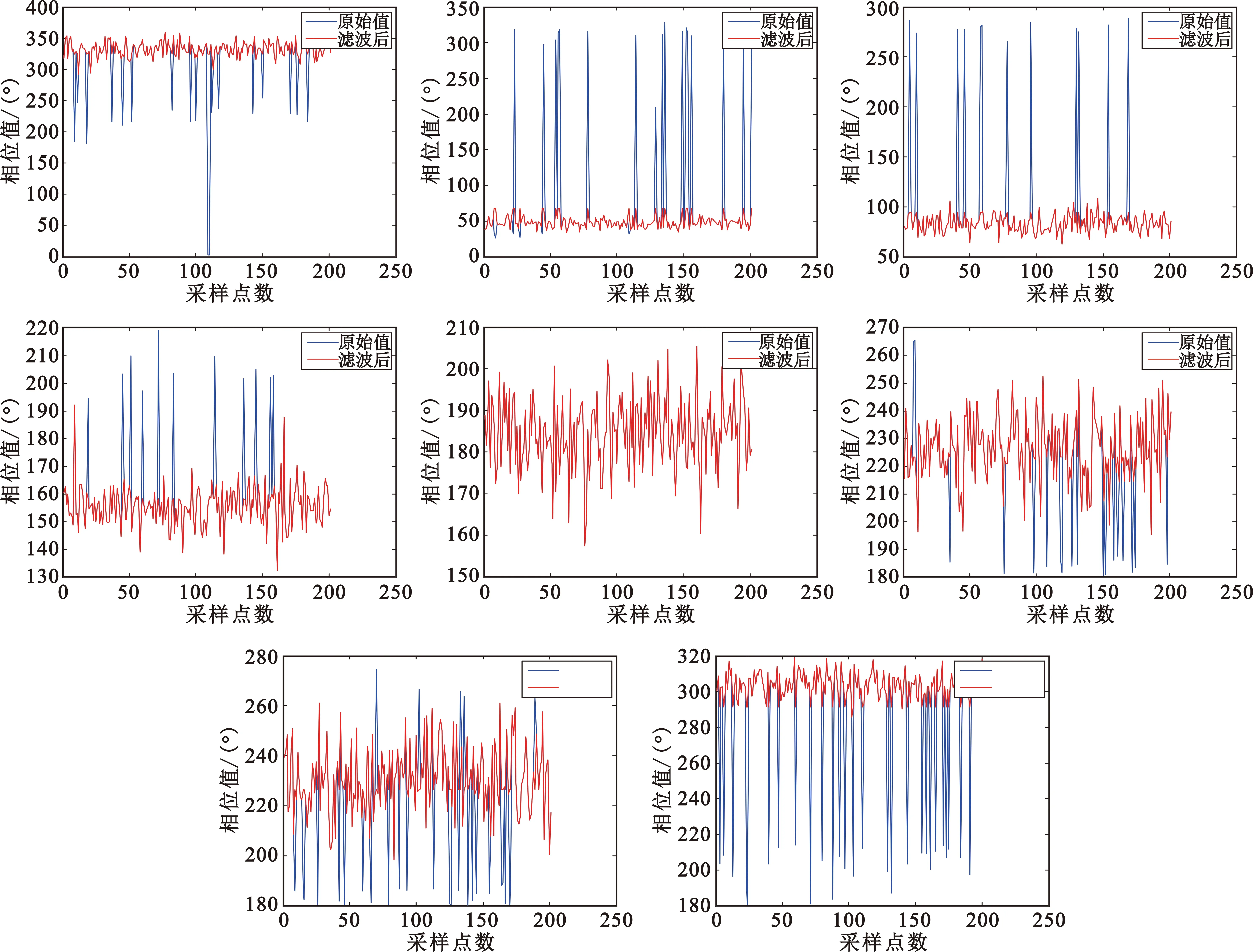
(a)8组滤波前后相位信号

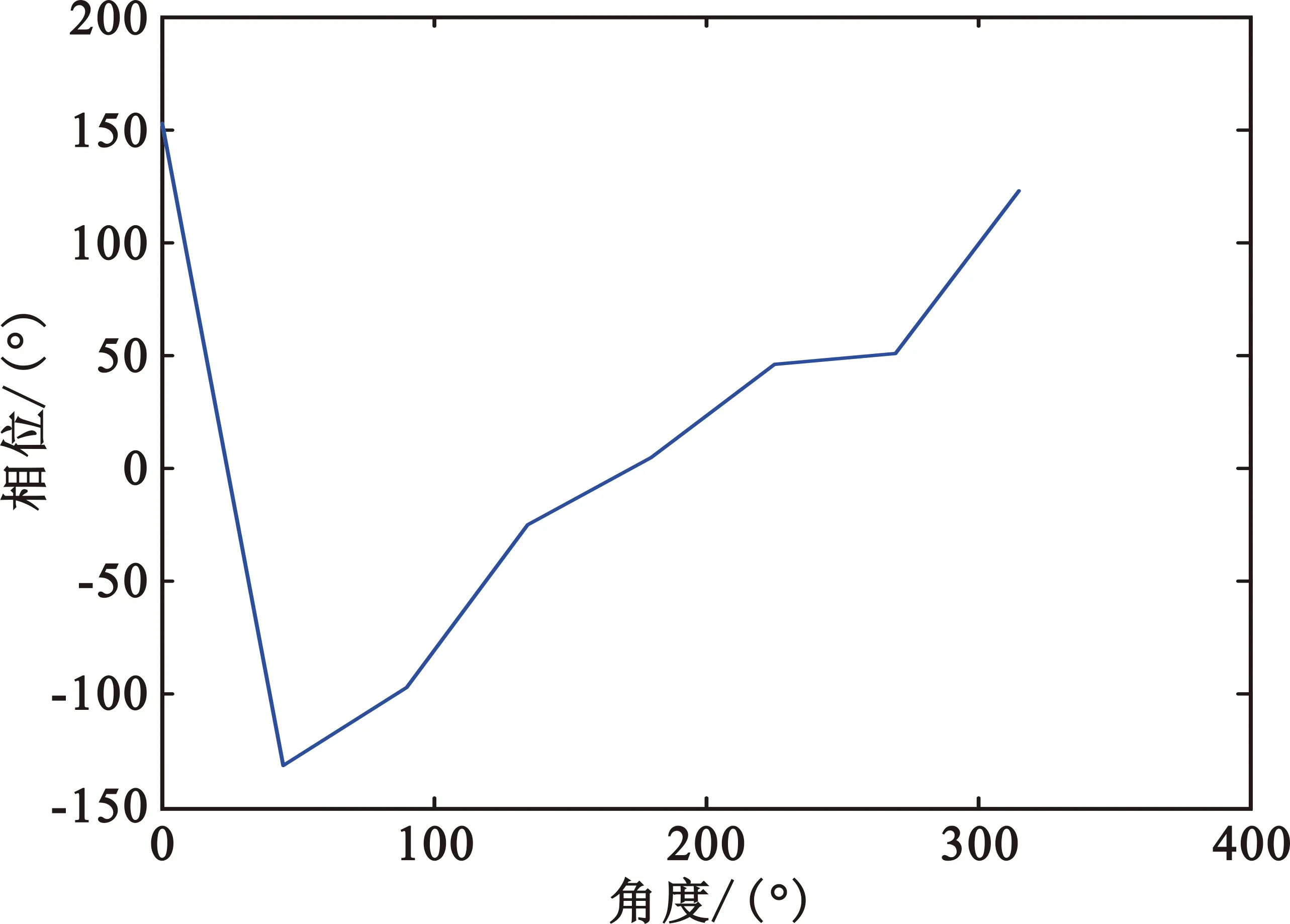
(b)相位变化

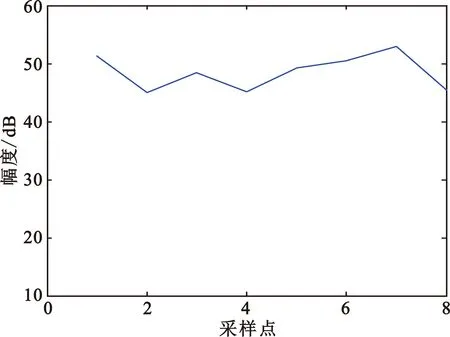
(c)幅度变化图7 天线阵列实测数据

为了更加直观地观测涡旋电磁波的模态数，采用谱分解法[16-17]对信号进行处理。由于涡旋电磁波的OAM具有正交性，可采用类似傅里叶变换的方法得到不同OAM所占比重，任何一个模态的涡旋电磁波都可看作由无穷多个模态叠加而成，即

(8)

(9)

式中：al为正实数，即模态占比，l表示模态数。采用谱分解法时，需要以波束轴为中心，对其圆周进行均匀采样得到幅度和相位的复信号，经过式(8)计算得到OAM谱图，如图8所示，(a)表示阵列天线仿真时的OAM谱图，OAM=+1的纯度约为90%，这是由于仿真阵列单元为4，数量不是足够大导致；(b)表示实测OAM谱图，由图可知OAM=+1的占比最大，约为50%，故本文设计的阵列天线能产生主模态数为+1涡旋电磁波。

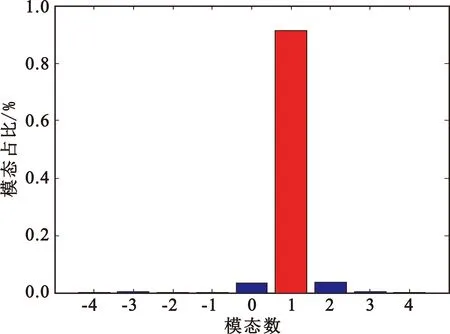
(a)仿真

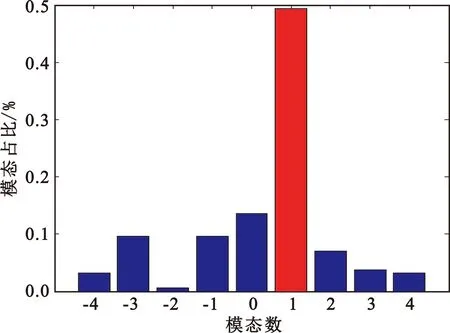
(b)实测图8 OAM谱图

由于主模态纯度与仿真相差较大，且实测中次模态数较多，主要是由各种实验误差造成，主要误差包括采样点数、中心轴偏轴接收、幅度误差、相位误差、噪声误差等。利用Matlab工具对以上几种误差分别进行仿真，得到如图9所示的误差曲线，曲线包括误差对不同OAM产生的影响。

由图9(a)可知，随着采样点数的增加，模态测量误差随之减小。在采样点数小于20个时，模态数越高，测量误差越大；在采样点数大于20时，各模态数之间的测量误差基本一致。由于实验条件有限，本实验采样点数为8，OAM=1的模态误差约为30%。

偏轴接收即收发天线中心轴之间存在偏离，若偏离圆阵中心轴的误差服从均匀分布Δd～U(-1 cm，1 cm)，由于不同区间范围所产生的误差不同，故设置最大偏轴区间为[-10 mm，10 mm]，仿真结果如图9(b)所示，随着偏轴误差区间的增大，对主模造成的测量误差也越大，而偏轴的影响对不同模态数造成的误差基本一致。

理论上应当保证各阵元等幅度等相位差，但由于实验器件产生误差，会引起幅度和相位差不等，设幅度误差服从均匀分布ΔAM～U(-5 dB,5 dB)，相位误差服从均匀分布Δphase～U(-5°,5°)，在不同区间范围内分析幅度和相位对不同模态数测量产生的误差影响，在每组区间进行50次仿真实验，其误差曲线如图9(c)、(d)所示。幅度和相位误差对低模态数的影响较小，对高模态数的影响较大，随着误差区间增大，产生涡旋电磁波的主模态纯度也会下降。对于OAM=1的涡旋电磁波，无论是幅度还是相位误差影响，主模态误差远于0.1，故OAM=1的涡旋电磁波具有很好的稳定性。对于8阵元天线，所能产生最大模态数为3，故OAM=3时其纯度必然不高，且高模态涡旋电磁波对涡旋中心处幅度值和相位值的变化更加敏感，故造成的误差也会越大。

噪声为高斯白噪声，在不同信噪比条件下分析噪声对不同模态数测量产生的误差影响，在每组区间进行50次仿真实验，其结果如图9(e)所示。随着信噪比的增加，涡旋电磁波的模态测量误差随之减小，低模态受噪声影响程度小，高模态受噪声影响程度大，当信噪比大于20 dB时，模态测量误差基本为零。

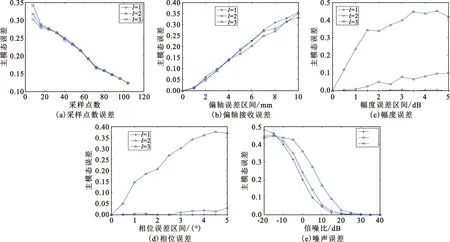
图9 误差曲线

综上误差分析可得，对于OAM为+1的涡旋电磁波，主要误差为采样点数和偏轴接收引起，实验环境在微波暗室，且信号经过滤波处理，故噪声误差可以忽略，8采样点导致主模误差30%，设偏轴误差区间为[-3 mm,3 mm]，主模误差约为10%，由此可估计本设计阵列天线产生涡旋电磁波主模纯度高达90%，与仿真实验一致，这表明了阵列天线的设计具有很好的可行性。

5 结束语

本文根据阵列天线理论和涡旋电磁波原理，推导了涡旋电磁波产生的数学模型，设计并实现了一款工作在X频段的均匀圆形阵列微带天线，采用同轴馈电方式，整个天线阵列直径120 mm，成本低，体积小，在中心频率处具有较低的回波损耗和良好的阻抗匹配。仿真和实测结果表明，在考虑采样点数误差和偏轴误差情况下，其产生的+1模态涡旋电磁波纯度可达90%，改变阵元数目和相位差可产生不同OAM的涡旋电磁波，具有良好的可重用性和稳定性。整个天线设计简单、易实现，为后续研究者们对涡旋电磁波的实测应用研究提供了便捷，但模态数越大，其能量越发散，因此，对高模态数、能量集中的涡旋电磁波还需进一步研究和更加深入地探讨。