湿陷性黄土微观颗粒力学特性研究

王志强

(中国电建市政建设集团有限公司，天津 300384)

0 引言

中国幅员辽阔，在中国西北、华北、东北等地区存在着广泛的黄土地貌，而且黄土组成成分复杂，在不同的自然环境下会产生不同的土体结构。黄土是一种典型的软土地基，典型的黄土受水分影响严重，黄土在遇水后状态会产生极大变化，当干燥的黄土被水侵入后，土体结构极易发生剥离和侵蚀，严重时甚至会发生湿陷[1]，湿陷性黄土在遇水前能保持自身的高强度和低压缩性，但当其浸水后，黄土对水的特殊敏感性会造成黄土发生变形突变，变形发生迅速且黄土自身强度明显下降，而且这种变化是非连续的和不可逆的[2]。加上被当地企业不合理的开发利用，黄土地区的水土流失问题已经十分严重。因此，对典型黄土的微细观结构以及破坏机理进行试验研究，对黄土的应力应变特性和抗剪强度等力学特性开展研究具有重要的实践意义。

在常规三轴实验方面，杨倩[3]选用的实验仪器为真三轴仪，在不同含水率、固结围压以及不同初始结构条件下，选择平面应变固结排水方法对黄土试样开展了三轴剪切试验，成功获取了在平面应变条件下试样黄土的各项强度特性，并分析得到了试样黄土结构性在全过程中衰减的演化规律。曾垂青[4]选取青海海北地区的黄土试样进行了常规三轴压缩试验，得出了固结应力比、围压以及应力路径对黄土强度及应力-应变特性的影响规律。赵杰[5]选取饱和原状黄土作为试样，采用固结排水的方法，在控制吸力条件下，进行了常规三轴剪切试验，选用常吸力加荷与常应力增湿两种模式进行对比，得出了原状黄土的变形、强度及屈服特性的影响规律。

在数值模拟方面，张策[6]通过对黄土进行真三轴试验剪切数值模拟，得出了不同含水率下，正常状态固结黄土和超固结黄土的强度、变形变化规律。苑伟娜等[7]采用颗粒流离散元数值软件建立黄土的三轴剪切模型，研究了在不同颗粒尺寸、形态以及不同排列方式的条件下，黄土的变形和结构强度所受到的影响。本文通过建立黄土试样三轴剪切模拟试验，研究了围压对黄土试样强度及应力-应变特性的影响规律。

1 数值模拟模型与方法

1.1 PFC颗粒流

PFC(Particle Flow Code)离散元数值模拟软件，是近年来常应用于重新经典力学实验模拟的一种细观分析软件，它可以从微细观角度模拟研究岩石的基本力学特性，通过将岩土体的细观参数与其宏观力学性质建立联系，从细观层面以具体到颗粒的方式来解释岩土体的损伤以及破坏机理。

1.2 PFC基本假设

1)所有颗粒视为刚体，颗粒接触后仍旧维持原有形状和大小。

2)颗粒接触方式均为点接触。

3)颗粒之间的相互作用通过力和力矩来实现，遵循力-位移原则。

4)颗粒之间可以存在重叠，但重叠量远远小于颗粒大小。

1.3 数值模型构建

通过建立三轴剪切数值模型探究黄土的微观力学特性，黄土颗粒流数值模型由颗粒组成，颗粒形状可以自定义，本文模型采用球形颗粒构建，三轴模型尺寸高为80 mm，直径为40 mm，颗粒流模型试样如图1所示。

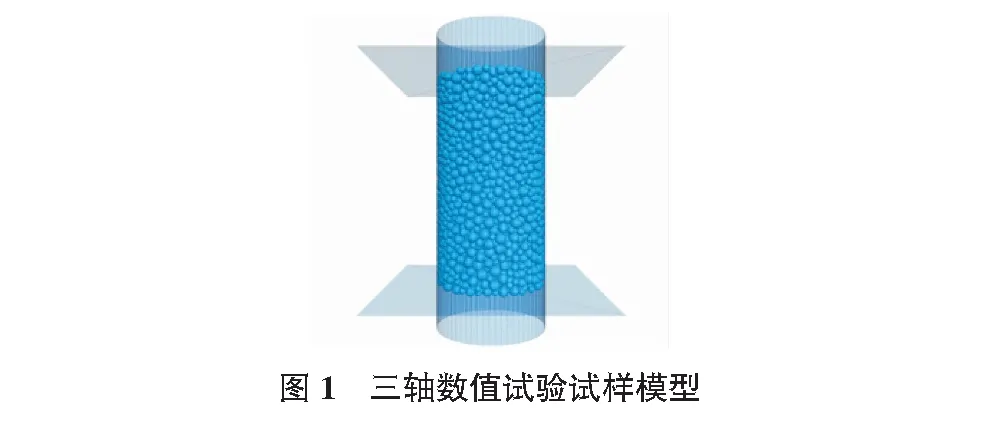
模型试样包含颗粒4 129个，其中接触9 091个，因为黄土土体抗压、抗剪，但不抗拉，一般选用线性接触模型或者接触黏结模型，本文模型选用接触黏结，并参考代表性的细观参数对模型赋值。模型边界墙体的法向刚度为1×1010N/m，颗粒法向刚度1×107N/m，墙体切向刚度为1×1010N/m，颗粒切向刚度采用1×107N/m。模型细观参数见表1。

表1 颗粒流数值模拟参数

模拟三轴剪切实验时，首先需要对试样施加围压，软件通过运行伺服控制程序来保持围压的稳定，实验的上下两侧水平墙为加载板，因为不能对墙体直接施加压力，所以通过对墙体施加速度的方式来对试样提供压力，侧面圆柱形墙体同理。加载速度设定为0.05 m/s。当试样的轴向应变增加到15%时终止加载。本次模拟在四种围压条件下加载，分别为50 kPa，100 kPa，150 kPa，200 kPa，在模拟试验中记录下试样加载过程中的偏应力、轴向应变、轴向应力、模型试样体应变等参数。

2 模型模拟结果分析

通过离散元数值模拟分析软件，模拟黄土的常规三轴剪切实验，得到了三轴实验的力学参数，通过对模型的力学性质，偏应力、轴向应变、轴向应力、模型试样体应变等信息进行综合分析，模拟分析结果如下。

2.1 应力-应变曲线分析

图2为模型试样在不同围压下的三轴剪切试验的应力-应变曲线。由图2可知，模型试样在三轴剪切时经历了多个发展阶段：

1)孔裂隙压密阶段:由于土体存在天然孔隙等初始损伤，尤其黄土土体多为大孔隙结构，在三轴实验过程中，试样被不断加压，颗粒之间的孔隙不断减小，因此这一阶段的应力-应变曲线表现为明显的上凹型，在该阶段加载过程中，环向应变远远小于轴向应变，几乎为0。

2)弹性变形阶段:土体孔隙减少后，颗粒结构之间的摩擦增加，表现为轴向应力与轴向应变基本可以维持线性关系，基本满足胡克定律。分析原因为，在土体压密之后，孔裂隙减小，土体颗粒摩擦增加，微裂隙面之间受到压缩的影响，极大减少了相互错动，试样形变过程表现为弹性。

3)变形局部化阶段:试样内部开始产生、扩展大量裂隙，裂隙逐渐联结，由微观分布开始向宏观裂隙过渡。应力应变曲线变化较为明显，斜率开始变缓，轴向应力即将到达最大值，并且环向应变的变化速率明显加快。

4)应变软化阶段:模型受力持续增加，达到极限后试样开始出现肉眼可见的裂纹，此时的土体发生明显破坏，土体承载能力丧失，由内部的裂隙面继续承担荷载。

由图2可知，围压对试样的变形产生的影响很明显：1)在孔裂隙压密阶段，随着围压的增加，试样初始孔裂隙受到压缩，孔裂隙压密阶段逐渐消失。2)随着围压的增大，应力应变曲线的斜率和峰值也明显增大，分析原因为，试样颗粒之间的孔隙随位移的增大而减小，土体的承载能力得到提升，弹性模量也随之增大。

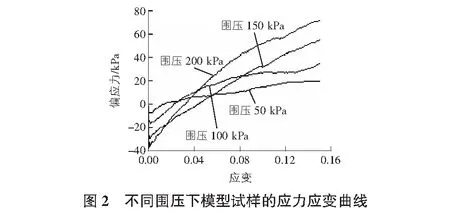
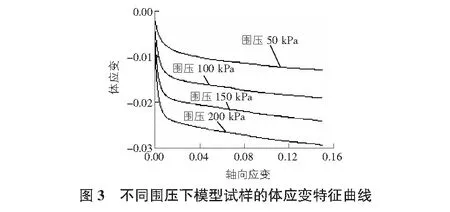
图3为不同围压下模型试样的体应变变化曲线。由图3可知，在三轴试验加载过程中，试样体应变曲线一直下降，试样发生剪缩现象。随着围压的增加，试样仍未达到应变软化阶段，所以一直处于剪缩状态。

2.2 力学参数分析

表2给出了黄土的三轴压缩数值模拟力学参数。表2中σ3为模型受到的围压；σp为试样的轴向偏应力峰值(σ1-σ3)；σs为试样的压缩峰值强度；Es为试样的弹性模量(取峰值强度30%～70%计算出的斜率)。具有如下关系：σs=σp+σ3。

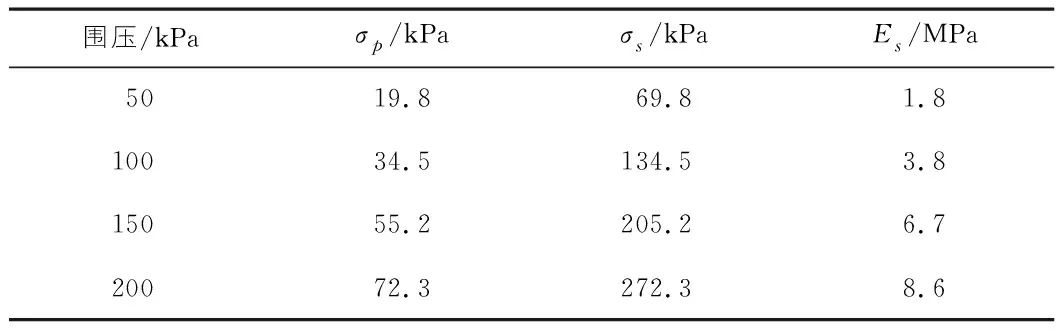
表2 数值模拟的强度变形参数结果

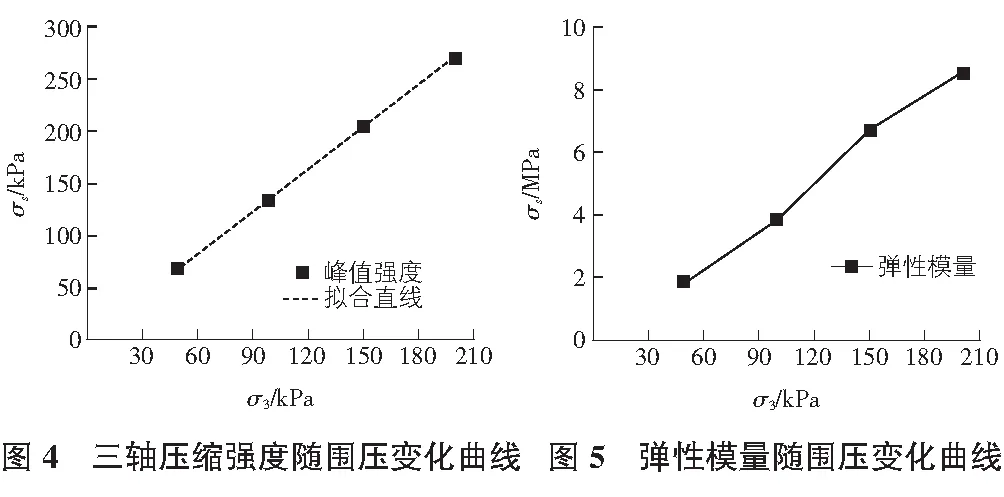
根据表2绘制黄土三轴压缩强度随围压变化关系数值模拟曲线图，如图4所示。由图4所示的关系曲线可见，试样的σs随着围压的增大而增大，可用一次线性函数加以拟合。拟合的函数关系式为：

σs=1.356σ3+897(R2=0.999 6)。

拟合直线的拟合系数接近等于1，这表明黄土试样的三轴压缩强度与围压保持正线性相关。

从图5所示的模拟的黄土试样弹性模量随围压变化曲线图中可以看出，试样的弹性模量随着围压的增加而增加，而且增幅较大。分析原因为，围压可以压缩试样中孔隙裂隙的空间，因此可以提高颗粒之间的有效接触面积，进而提高试样的弹性模量，黄土试样孔隙裂隙较大，实验加载的围压不断提高颗粒之间的有效接触面积，因此其弹性模量的增长幅度很明显，这也与三轴实验的结论经验相一致。

3 结论

构建了黄土试样的数值模型，模拟了常规三轴室内剪切试验，对实验结果进行了力学特性分析。本章得到的主要结论如下：

本文选取的三轴剪切数值模型对黄土试样的力学行为有较好的体现。

1)随着围压的增加，试样应力-应变曲线变化明显，斜率和峰值明显增大。

2)加载过程中黄土试样体应变曲线不断下降，试样发生剪缩现象且随着围压的增加剪缩程度更加明显。

3)试样的弹性模量受围压影响明显，随着围压的增加弹性模量增幅较大，这是因为，黄土试样孔隙裂隙较大，弹性模量的增长幅度受围压影响很明显。

4)三轴压缩峰值强度与围压保持正线性相关，拟合方程为σs=1.356σ3+897，相关系数R2=0.999 6，拟合程度较好。