角膜神经显微图像的自适应渐晕校正

李天宇，李光旭，2*，张 琛，李方烃，李德衡

（1.天津工业大学 电子与信息工程学院，天津 300387；2.天津市光电检测技术与系统重点实验室，天津 300387；3.天津医科大学眼科医院 眼视光学院，天津 300384；4.国家眼耳鼻喉疾病临床医学研究中心天津市分中心，天津 300384；5.天津市视网膜功能与疾病重点实验室，天津 300384；6.北京大学人民医院眼科，北京 100044；7.瑞达昇医疗科技有限公司，北京 101100）

1 引言

角膜中存在丰富的感觉神经末梢，这些角膜神经可调控泪液分泌，为上皮细胞和基质细胞提供营养支持［1］。同时，角膜神经功能障碍可引起结构变化的出现［2］。角膜也是人体唯一能够直接观察到神经末梢的组织。角膜神经的形态及密度变化可为神经类疾病，如糖尿病周围神经病变［3］、退行性帕金森症［4］等对神经系统的影响提供直接证据。此外，圆锥角膜等疾病也会引发角膜局部形态病变，导致角膜神经曲折度明显增加，交织成网状，临床表现为不规则散光等［5］。

近年来，激光共聚焦显微镜（Laser Scanning Confocal Microscopy，LSCM）的广泛应用［6］使对角膜神经形态特征的研究得以实现［7］。由于单张角膜共聚焦显微图像成像范围较小［8］，为获得更大范围内角膜神经的整体形态分布，临床上利用图像拼接技术在保持相同分辨率的前提下扩大角膜图像的可视区域［9］。然而，随着离轴距离的增加，光线经过光学系统的有效孔径减小，导致了从中心到边缘非线性的缓慢的光衰减，图像呈现出中心亮四周暗的特征，称为光学渐晕效应［10-11］。该效应会引入拼接伪影，增大角膜神经的重构难度。

图像渐晕校正算法可分为两大类［12］：基于像素分析的校正方法和基于渐晕数学模型的校正方法。

基于像素分析的方法无须建立渐晕模型，直接在空间域或频域对渐晕图像进行校正替换操作。Zheng等人［13］提出真实图像在像素梯度中服从稀疏概率分布，其特点是在梯度分布中有一个高峰度和两个重尾。利用图像的分段恒常性理论调整医学图像中的亮度不均衡现象，通过计算图像梯度直方图后拟合最大似然系数，使用迭代加权最小二乘法算法（IRLS）进行求解。Chernavskaia等人［14］提出了一种基于傅里叶变换的频域滤波方法校正序列图像渐晕。序列图像空间域中的周期性渐晕导致频域中出现周期性结构。通过改变频域中的这种结构消除图像空间域的渐晕现象。但显微拼接图像在空间域重叠的情况下不存在周期性，故不适用于角膜神经图像。

基于渐晕数学模型的校正方法是先对渐晕效应建模，再将渐晕模型函数的逆函数作为增益函数，反向补偿原图像达到校正的作用。D'Angelo等人［15］参考cos4θ模型函数，建立了高次线形径向渐晕模型，并用于相机光学系统渐晕效果校正。Goldman等 人［11］根 据 相 机 的 光 圈 大 小、焦距、辐射亮度和快门持续时间等外部固定参数来建立渐晕模型，但对于不同的相机拍摄图像需进行不同的设置。Smith等人［16］提出了一种使用正则化能量最小化（CIDRE）的方法来校正图像光照强度分布。首先构造一个线性光照强度模型，在求解模型时使用稳健的正则化能量函数，并使用Limited-memory Broyden-fletcher-goldfarbshan（L-BFGS）数值优化算法求解优化。Peng等人［17］提出了一种基于低秩和稀疏分解的图像渐晕校正方法（BaSiC）。首先构造一个测量矩阵。然后分解成一个低秩矩阵和稀疏残差矩阵，使用线性化的拉格朗日增广方法迭代方式求解优化，最终获得渐晕阴影模型。但需要多幅连续的图像且每个要处理的图像的前景与其他每个图像的前景不相关，否则该方法会将视野中心始终较高的图像强度视为局部亮度的增加，从而消除了真实的图像亮度变化。

上述算法虽然可以解决单个或组合序列图像的渐晕问题，但需针对特定图像进行参数设置。如设置不当，会出现图像欠校正或过度校正等问题。对于角膜神经图像而言，医生采样角膜神经进行镜头移动时，采样移动方向不固定，导致角膜神经图像序列不规律。此外，因显微镜采样速度较快，图像间相关性较高等原因，导致采样图像通常无法满足以上算法条件。因此，本文提出一种角膜神经显微图像自适应渐晕校正算法，针对共聚焦显微镜的渐晕效应，提出使用六阶多项式对渐晕模型进行拟合，更好地保留原图像未受渐晕影响区域的特征并校正渐晕区域。在校正过程中使用对数信息熵对建模效果进行评估反馈，增强了渐晕校正效果的稳定性。

2 方法原理

2.1 渐晕模型的构建与补偿

图1（a）是含有渐晕效应的角膜神经共聚焦显微图像，直观上可以看出图像边界区域比中心区域亮度低。渐晕效果以图像光学中心为原点，向外渐晕强度逐渐增加。渐晕呈对称性分布，且渐晕强度随径向距离的增加而增大。图1（b）为拼接后角膜神经显微图像。图中渐晕失真会在图像拼接处产生伪影，造成角膜神经结构不清晰。图1（c）表示图1（a）图中对角线处（黄色虚线）像素的亮度变化趋势。蓝色实线表示对角线像素值曲线，红色虚线表示像素变化拟合曲线。图像中心部分区域为非渐晕区域，渐晕校正方法的目的为调整渐晕区域像素值，使其接近非渐晕区域像素值。

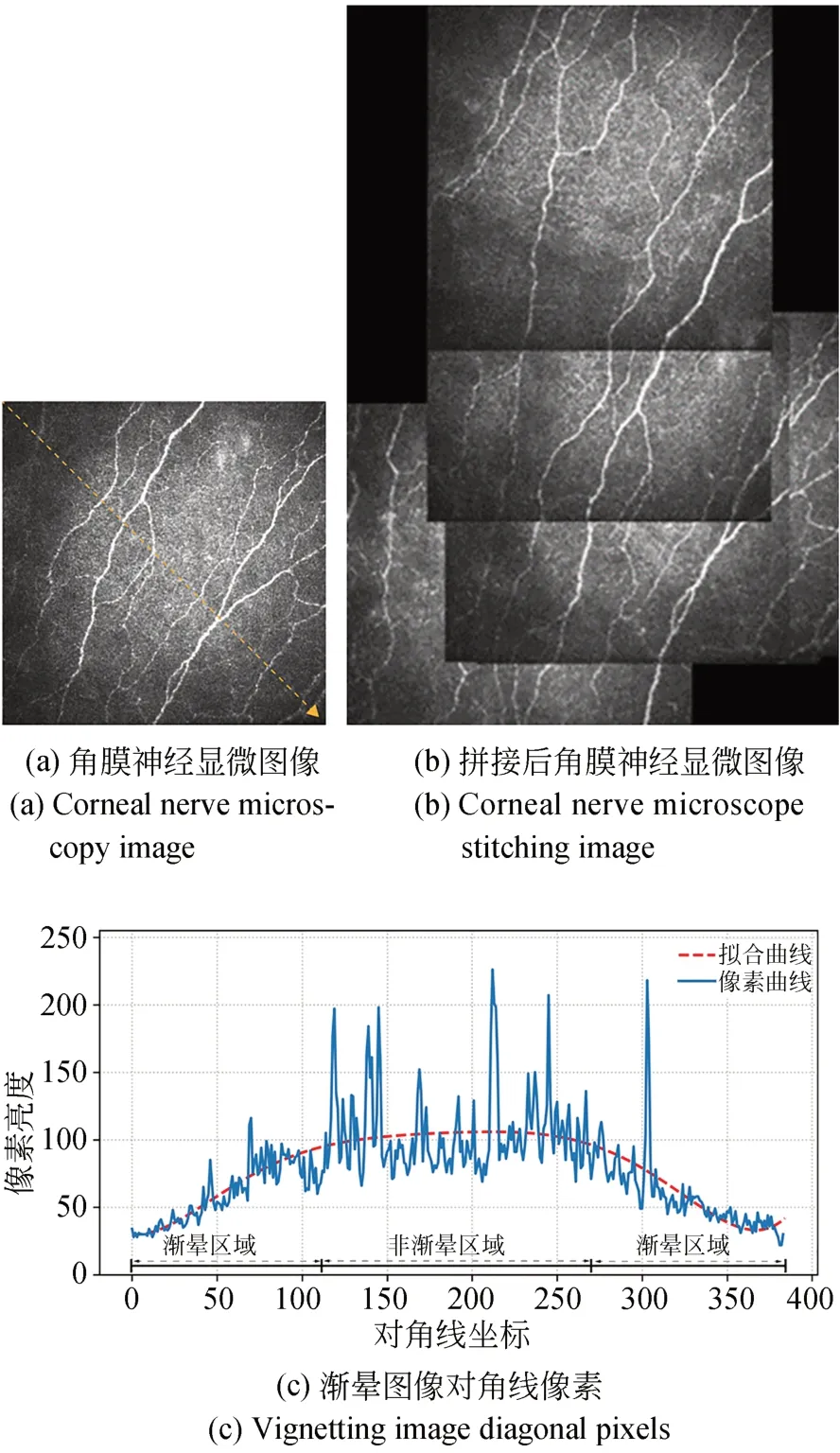
图1 图像中的渐晕效应Fig.1 Vignetting effect in the image

共聚焦显微镜的光源光路与成像光路相同，其成像亮度值呈现中心高并向四周逐渐减弱的特点［18］，如图2所示。通常，受光路影响显微镜组的光学中心（渐晕中心）与获取的图像中心有坐标偏差，其偏移量最大可达25个像素［19］。然而，共聚焦显微镜采用平移扫描的方式获取图像。且单次成像范围极小，成像位置偏差可以忽略。因此，可将光学中心与图像中心视为同轴。

图2 渐晕效应衰减模型Fig.2 Vignetting effect decay model

基于渐晕数学模型的校正方法是将渐晕函数的逆函数作为增益函数M，反向补偿原图像像素灰度值。若用Iorg（x，y）表示包含光学渐晕效应图像。渐晕校正后图像为Ires（x，y），则：

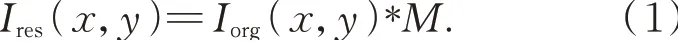
本研究利用相机响应模型EMoR［20］来拟合渐晕效果，该模型为含有偶次项的六阶多项式函数，可以用非常少的参数来模拟范围广泛的响应函数，并且在准确性方面优于其他多项式和非参数模型。进而求得其增益补偿函数为：

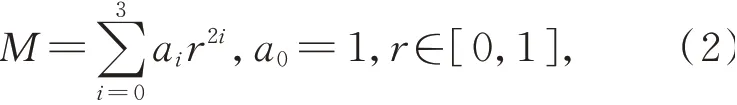
其中：r是图像像素点到图像中心点的归一化距离，令图像中心点处r=0，图像四个角点处的r=1；系数ai（i=1，2，3）称为渐晕参数，通过迭代优化求解。

2.2 渐晕参数存在条件

渐晕效果由中心点向四周递增，像素值向四周单调递减，所以增益函数必须单调递增：

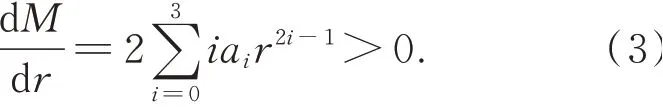
若令q=r2，则式（3）可化简为：

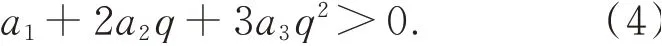
利用求根公式可得：

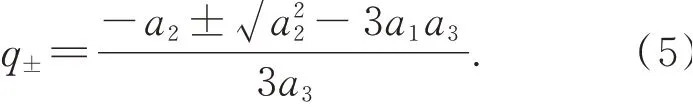
根据解的分布，得出当渐晕参数满足如下条件之一时，不等式（4）成立。

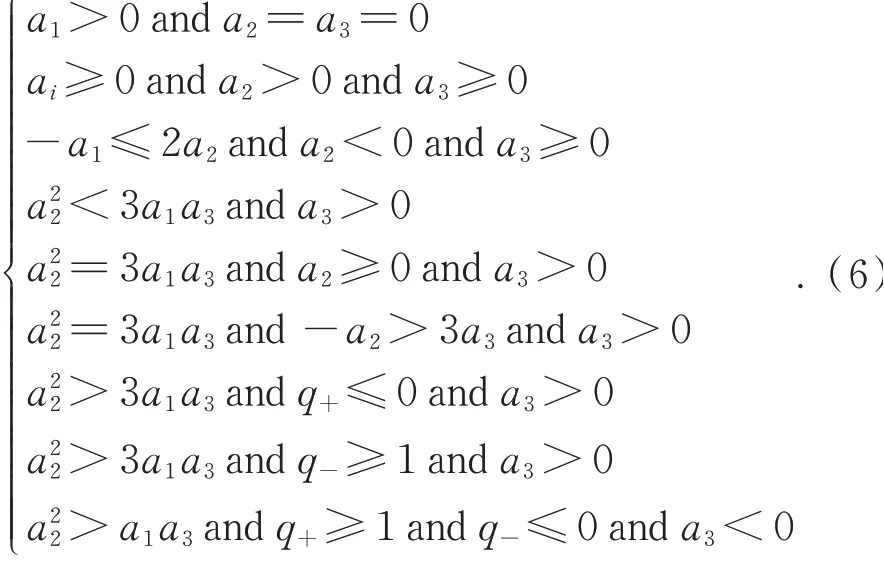
2.3 渐晕校正评价函数

当距离r变化时，上述限定条件可以保证渐晕参数取值的合理性。然而，由于渐晕模型采用六阶多项式很难直接求得最优解。为此，本研究通过评估图像信息熵来控制参数优化过程，以最小化图像信息熵的方法优化渐晕校正结果。

Likar等［21］提出通过最小化图像的信息熵对图像像素强度一致性进行评估，并将其用于渐晕伪影的校正模型的评估。通常，渐晕图像周围的暗角会使图像产生额外的信息熵；当渐晕被校正同时信息熵应该逐渐减小。然而，在此过程中过度校正会引入部分使图像增亮的信息熵，导致校正算法无法实现全局最优。

文献［22］证明了对数信息熵在参数优化过程中相较于信息熵的优越性。图3为信息熵与分布移动的关系比较。黑色曲线代表图像中未受到渐晕效应影响的区域（图像中心部分）的熵值分布；灰色曲线代表图像含有渐晕效应的区域（图像边界部分）熵的分布。通过渐晕迭代校正，图像亮度差别逐渐消失，即灰色曲线向黑色曲线靠近直至重叠。图3的第一行表示直接计算的信息熵。在渐晕校正的过程中，会因校正渐晕引起图像亮度增加而造成总信息熵增加，直到两个分布重叠时总信息熵开始减小。图3第二行表示对数信息熵计算结果。可以看出在移动过程中对数信息熵基本保持不变，直到两个分布开始重叠，对数信息熵才开始减小。因此，对数信息熵在优化过程中具有单调性。

图3 信息熵与分布移动的关系［22］Fig.3 Relationship between information entropy and distribution movement［22］

信息熵与对数信息熵计算公式虽然相同，在计算对数信息熵时，首先要将图像的像素值L进行对数映射，如公式7所示。

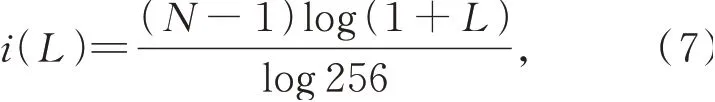
其中：N为映射后的像素阶数，i为对数映射后的像素值。在统计其直方图时，nk表示每一阶像素直方图的统计值。运算符■■与■■分别表示向上取整和向下取整。

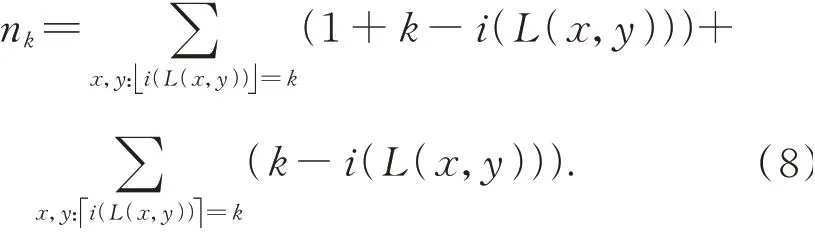
假设像素的对数信息熵趋于高斯分布，为减小量化误差，使用标准高斯核Gσ平滑直方图。用p̂k表示每个直方图区间的离散概率。

则对数信息熵H为：

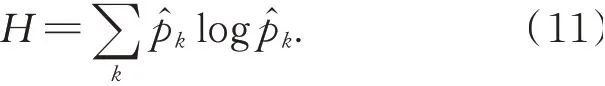
2.4 模型优化

采用Levenberg-Marquardt非线性优化方法获取参数的最优解。获得所需渐晕校正模型需要设定渐晕参数ai的初始值及递进步长δ。每个参数都会独立地增减相同的δ。每轮优化会产生6组计算参数，记作Vi（i=1，2…，6）。选取6组参数中最小对数信息熵对应的渐晕参数，直至H收敛。具体校正算法如下：

输入：渐晕图像I。

输出：校正图像C。

Step1：设置渐晕参数初始值a1，a2，a3=（0，0，0），优化步长δ=1/2，对数强度熵最小值Hmin=H（I），C=I，停止阈值T=1/256。Step2：当δ＞T，计算6组渐晕参数Vi，

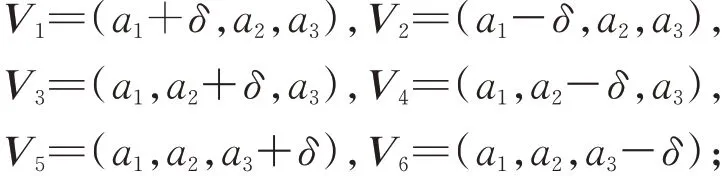
否则，结束优化。

Step3：如果Vi满足公式（6）中的条件之一，计算对数强度熵H=H（Vi）；若均不满足条件，转Step2。

Step4：如果H＜Hmin，Hmin=H；C=I·MVi；

否则δ=0.5*δ，转至Step2。

实验过程中，递进步长δ的初始值为1，每次迭代减为之前的一半，即δi=0.5*δi-1。图4显示了一组迭代优化过程中对数强度熵的变化。前期实验发现，当迭代次数大于40时对数强度熵趋于平稳。

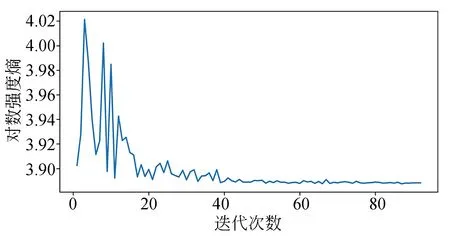
图4 对数强度熵迭代过程Fig.4 Logarithmic intensity entropy iterative process

3 实验与结果分析

本文以角膜共聚焦显微镜图像为研究对象，完成单幅图像的渐晕校正及全景图像拼接。为了更好地验证算法的有效性与可靠性，将提出的算法与针对相同图像特性（非自然图像）的算法进行对比，包括基于医学图像渐晕校正的非建模算 法［13］，基 于 显 微 图 像 渐 晕 校 正 的CIDRE算法［16］和BaSiC算法［17］。

3.1 实验材料

实验选取5名患者双眼的角膜共聚焦显微图像，每组包含图像的数量为300～900张不等。图像由海德堡视网膜激光断层扫描系统（Ⅱ代）获取。视场大小为400 μm×400 μm，最高分辨率为1 μm。

3.2 主观性评价

图5为一组渐晕校正前后角膜显微图像对比图。将单张原始图像先进行渐晕校正处理，再进行手动拼接。可以直观看出，校正后图像亮度分布均匀，且图像拼接处无伪影，衔接自然。

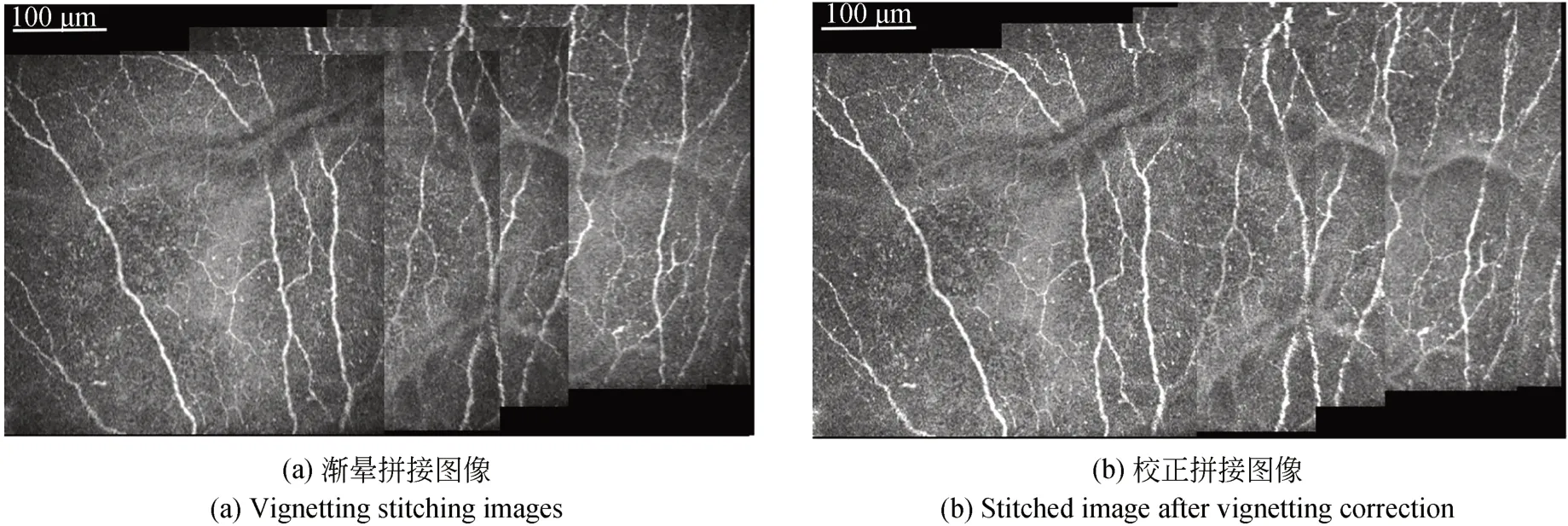
图5 渐晕校正前后图像Fig.5 Images before and after vignetting correction

3.3 客观性评价

为了客观评估渐晕校正对于角膜神经图像的有效性，我们对比了校正前后2幅图像局部灰度值变化。如图6（a）所示，以图像中心为原点，求取固定像素宽度的环形区域内像素的平均值。图6（b）为当环形区域宽度取10个像素值时，校正前后像素均值的变化曲线。由图6（b）渐晕图像曲线可以看出像素均值由内到外呈递减趋势。表明渐晕效果是从图像中心向外亮度逐渐降低，且随着距离增大，渐晕强度逐渐增加，符合渐晕效果的物理性质。BaSiC方法与CIDRE方法虽然可以较好地校正渐晕，但中心区域像素明显降低，改变了原始图像的亮度，会对后续医生诊断产生影响。非建模方法虽然中心区域像素均值下降不明显，但随着圈层数增加，渐晕校正效果有所降低。本文提出的方法校正后图像周围区域像素无明显增减趋势，亮度均衡。可证明渐晕校正效果良好。图7为不同渐晕校正方法的结果。

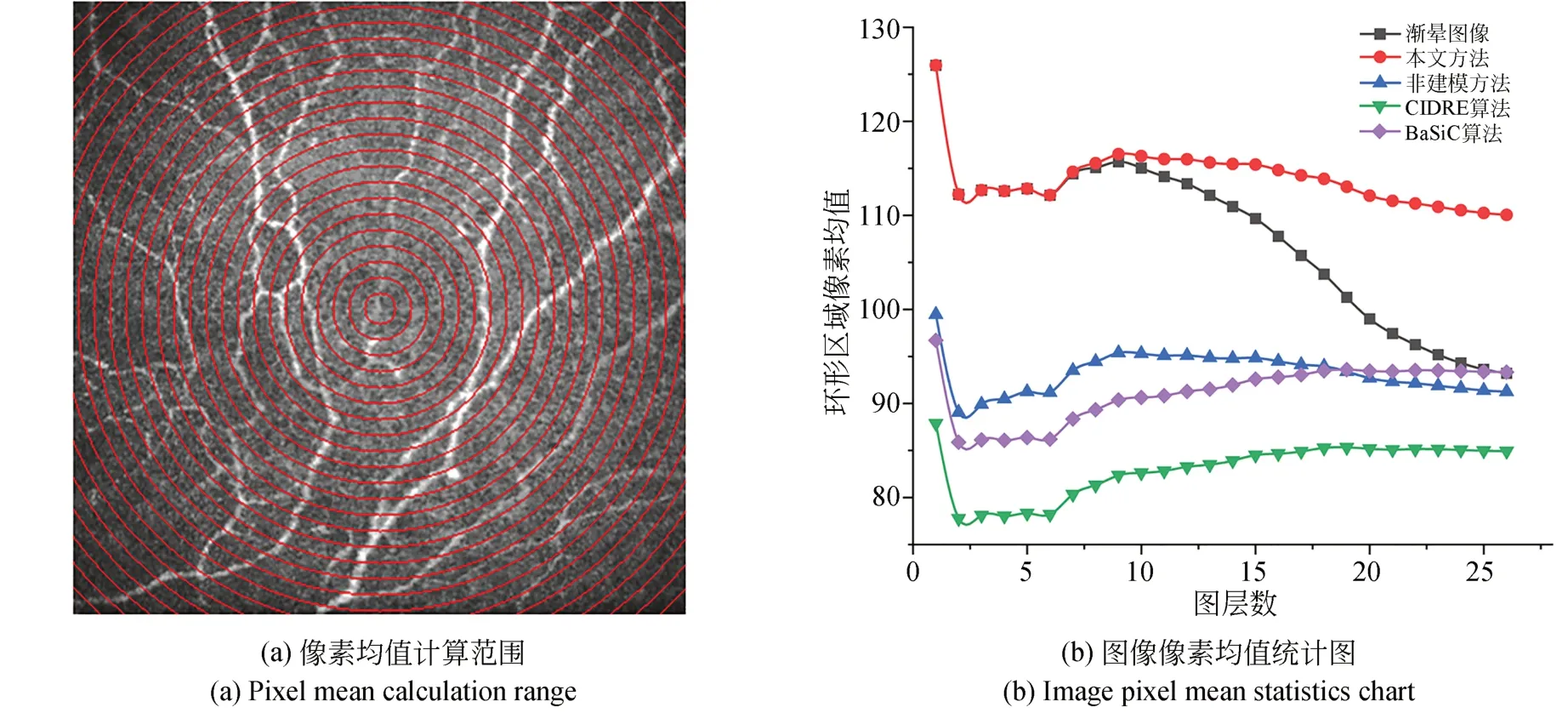
图6 渐晕校正图像像素法评估Fig.6 Pixel method evaluation of vignetting corrected image

图7 不同渐晕校正方法的结果Fig.7 Results of different vignetting correction methods

本文收集了5例不同患者的角膜神经图像，每例图像的光照和采集深度条件均不同。为了客观评估渐晕校正效果的有效性和可靠性，我们以正常图像为基准图像，再对基准图像人为添加渐晕效果，获得模拟渐晕图像供校正使用。将正常图像与校正后图像比较计算均方误差（Mean Square Error，MSE）、峰值信噪比（Peak Signal to Noise Ratio，PSNR）、结构相似性（Structural Similarity，SSIM）［23］的平均值，对比评估不同渐晕校正方法结果的图像质量。

本论文引入SSIM对校正前后图片进行相似性计算，从亮度、对比度、结构三个方面评估渐晕校正算法的可靠性，分析算法对图像质量的影响。公式（12）为图像I1，I2间的结构相似性指数的计算公式。

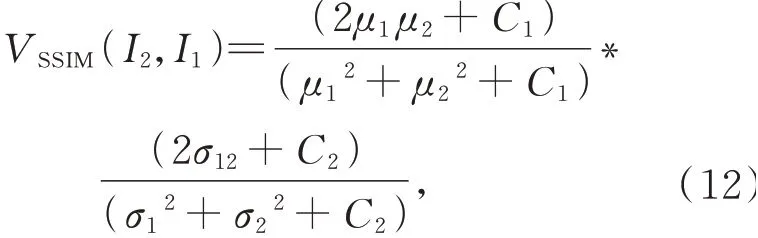
其中：μ1，μ2，σ1，σ2分别为对应图像的均值和方差；σ12为协方差。用均值、方差、协方差作为图像的亮度、对比度、结构的估计。SSIM取值范围为［0，1］。SSIM值越大表示两幅图像相似性越高，亮度与结构误差越小。

本文同时采用MSE计算图像像素差异的L2范数。MSE值越小代表图像像素误差越小，图像质量越好。PSNR能够反应图像的失真程度，PSNR值越大，图像失真越小。我们将图像PSNR范围限定在0～100 dB。

5组图像的数量分别为587、943、371、593和754组，其中病例A和病例B为正常采集组，其余病例图像采集特性分别为采集亮度低、采集亮度高、采集深度浅（部分显微图像出现噪声）。五名患者校正效果评估平均结果如表1所示，本文方法处理的5名患者校正后图像MSE、PSNR、SSIM平均值均高于其他方法，即校正后图像与基准图像最相似，具有最佳的校正效果。由此也可以表明本文方法渐晕校正后图像并未出现较大程度失真，不会改变原始图像中的亮度与结构等信息。图8绘制了5组图像校正后的评估指标箱型图。从图中可以看出本文方法相较于其他算法更加稳定，不会受其他外部因素影响，鲁棒性较高。

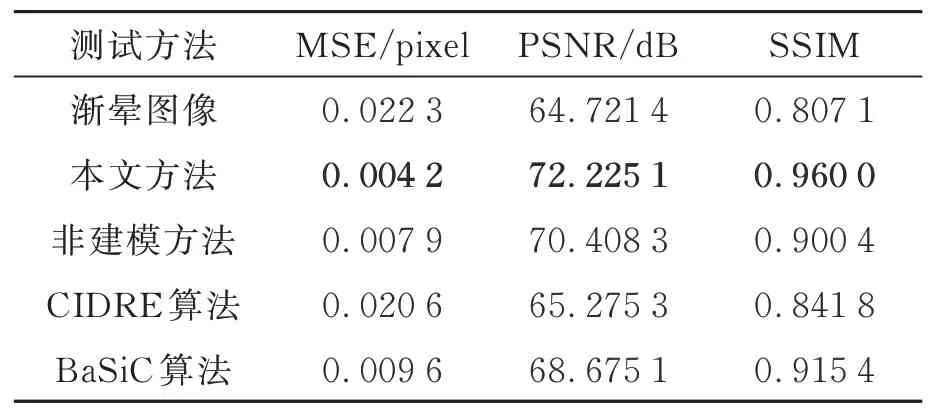
表1 五名患者校正效果评估平均结果Tab.1 Mean results of correction effect evaluation in five patients

3.4 角膜共聚焦显微图像拼接

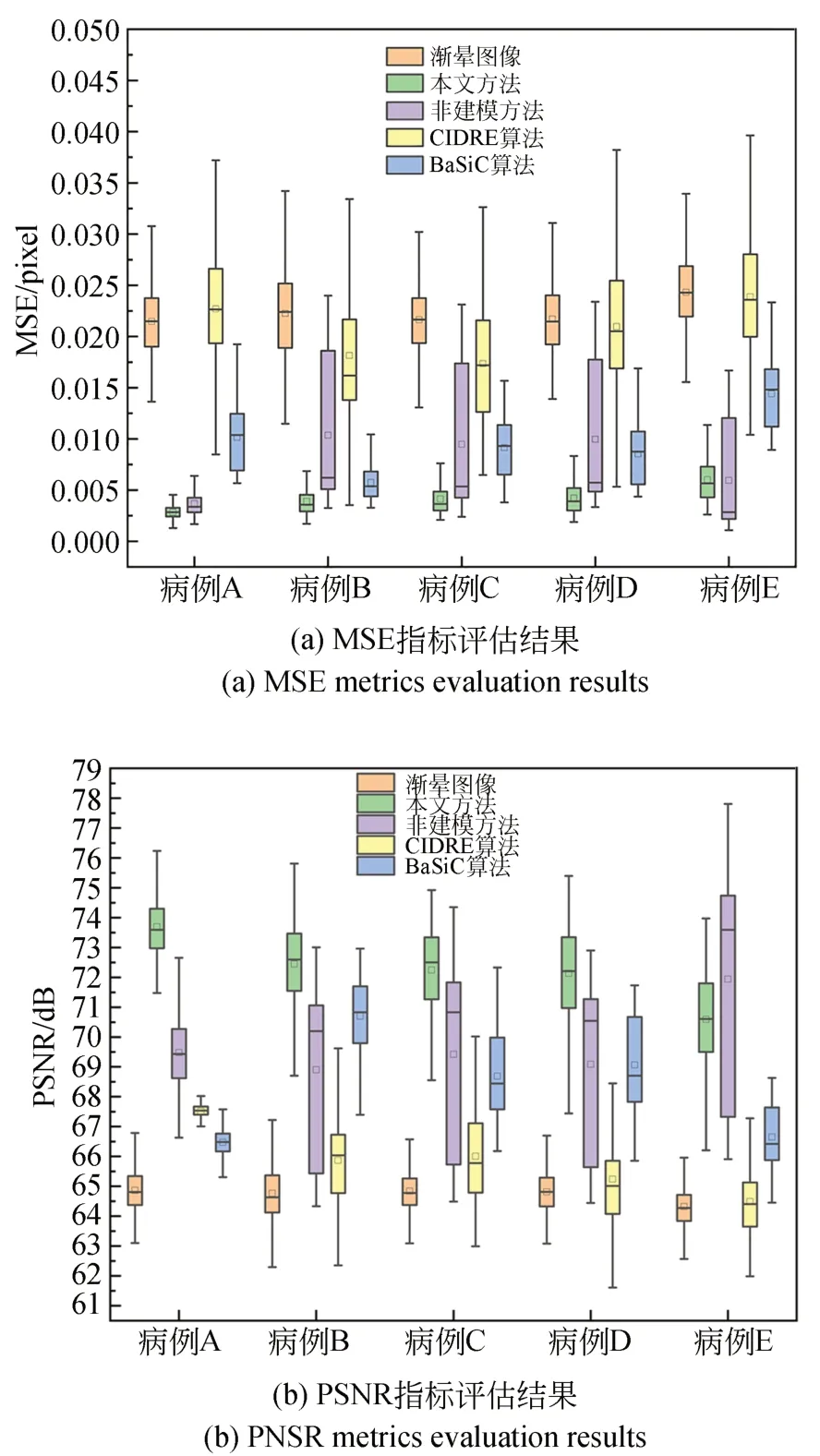
图9展示了2组渐晕校正前后手动拼接的角膜神经显微图像。第一行图像是由未进行渐晕校正的角膜神经显微图像拼接成的图像。第二行是由本文方法渐晕校正处理后进行的拼接图像。可以看出本文方法能够改善拼接图像衔接处的伪影问题。然而在实践中我们也发现校正前后待拼接图像间整体灰度值差别较大，影响后 续神经提取。为此在图像拼接前，我们对渐晕校正后图像的像素均值进行了图像直方图均衡化处理.

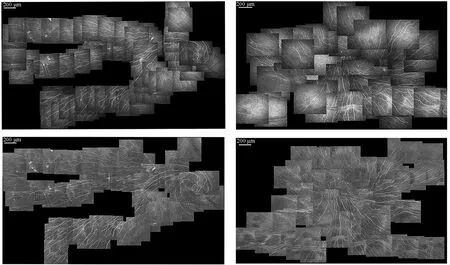
图9 角膜神经显微拼接图像Fig.9 Corneal nerve microscope stitching images

4 结论

本文根据共聚焦显微镜成像的特点，提出一种角膜神经显微图像的渐晕校正方法，介绍了渐晕效应并使用六阶偶次多项式建立渐晕效应的数学模型，采用Levenberg-Marquardt优化方法进行参数迭代优化，并设置限制条件进行约束。在优化过程中使用对数信息熵对渐晕数学模型进行评估。实验证明本文所述算法能很好地消除角膜神经图像的渐晕效果，避免角膜拼接图像产生伪影。校正后图像MSE、PSNR、SSIM评估指标平均值分别达到0.004 2、72.225 1 dB、0.960 0。渐晕校正后具有大视野范围的角膜神经显微拼接图像满足医生临床诊断需求。