基于理性密码学的分布式隐私保护数据挖掘框架*

程小刚,郭 韧,周长利

(1.华侨大学计算机科学与技术学院，福建 厦门 361021；2.厦门市数据安全与区块链技术重点实验室，福建 厦门 361021;3.华侨大学工商管理学院，福建 泉州 362021)

1 引言

在今天的大数据时代，数据挖掘技术越来越重要，因其是从大量数据中发掘出有价值的信息或知识的有效手段。数据挖掘中的一个研究重点是如何保护个人隐私。

一种常用的保护隐私的方法是对数据添加噪声，即在公布数据供科学研究之前对数据模糊化。首先一些标识字段，如姓名、身份证号码等,必须要删除或模糊化处理，但仅仅如此简单处理还不能有效保护隐私，因为通过其他一些准标识符字段，如年龄、性别和住址等，可以很容易推出此人的具体身份。为此，研究人员提出了一些更强的隐私保护手段，如k-匿名性[1]、l-多样性[2]和t-相似性[3]及差分隐私保护[4]等。k-匿名性就是通过加上噪声，使得发布的数据中存在至少k个在准标识符上不可区分的记录；在k-匿名性的基础之上提出的l-多样性要求每个相同的准标识符下至少有l类条目；t-相似性要求在任何等价类中敏感属性的分布同整体的分布是相似的；差分隐私保护是用于对数据库进行统计查询时，在最大化查询准确性的同时最大程度地降低识别出某条记录的概率。

加入噪声可以保护隐私，但同时也会降低数据的准确性，所以若采用此种方法就需要在隐私保护和数据的准确性之间寻求一个平衡。有没有既能保护隐私又能保证数据准确的数据挖掘方法呢？解决方案之一是分布式隐私保护数据挖掘，在此情形下隐私数据是由参与的各方拥有，然后各方通过合作来进行数据挖掘，挖掘出统计数据或函数结果的同时又不泄露各方的私有数据。这就是密码学中的核心问题——安全多方计算SMPC(Secure Multi-Party Computation)[5],这方面有众多理论研究成果和实现方案[6-11]，但经典密码学中的实现方案大都是理论性的结果，效率较低,不能应用于实际。比如，利用Yao[5]提出的加密电路(Garbled Circuit)方案在实现SMPC时，首先把需要实现的函数转换为等价的布尔电路(与门、或门、非门等构成的电路)，该电路可能非常庞大，实现起来效率极低，无法应用于实际。本文的目的之一就是提高分布式隐私保护数据挖掘的效率。

另外,本文从实际和理性参与方的角度来考虑分布式隐私保护数据挖掘问题，而不是像经典密码学中所有的参与方都被简单地划分为诚实方或恶意方。本文假设各个参与方都是理性的，在此基础上提出实现许多数据挖掘函数的高效协议，如求和、平均数、求积、频繁数据项等。

理性密码学是一个结合了博弈论与密码学的研究领域[12-16]。文献[17]研究了理性的秘密分享方案。Gordon等[18]对文献[17]的方案进行了改进。文献[19]提出K-弹性纳什均衡的概念，是对经典纳什均衡概念的加强，在此种均衡下，即使K个参与方共谋也不能提升他们的收益(传统的纳什均衡中K=1)。文献[20]考虑了如何构建实用的隐私保护数据挖掘PPDM(Privacy-Preserving Data Mining)软件工具箱，同本文的区别在于文献[20]没有半可信的第三方TP(Third Party)，而且不是从理性密码学的角度来分析其安全性，所以本文的方案更高效、更安全。

本文给出了理性PPDM R-PPDM(Rational PPDM)框架和一些常用统计函数的具体例子，对本文构建的方案进行了安全分析，最后进行了总结并给出下一步研究的方向。

2 R-PPDM方案构建

2.1 R-PPDM具体方案构建

(1)求和。

设有n(n≥2)个参与方，每个参与方持有一个秘密数字Si(1≤i≤n)，数据挖掘方Miner希望计算所有Si之和，即:

S=S1+S2+S3+…+Sn

而每个参与方又不想公布共同拥有的秘密数字，因可能会涉及隐私,如Si可能代表的是工资、年龄、身高、体重、血压等，即参与方的隐私要得到保护，在此前提下，各方愿意配合Miner来计算S值。

一个简单的解决方案如下所示：

步骤1参与方Pi随机选择一个参与方Pj(i≠j,1≤i,j≤n)，并用两方秘钥分发协议[21]或量子秘钥分发(Quantum Key Distribution)协议[22]等，来共同生成一个随机数Rij；

步骤2参与方Pi更新其秘密Si为S′i=Si+Rij，参与方Pj更新其秘密值为S′j=Sj-Rij；

步骤3各方把更新后的秘密数字发送给Miner，Miner执行以下计算得到S′：

S′=S′1+S′2+S′3+…+S′n

显然,虽然Si≠S′i,但S=S′。

图1是一个有4个参与方(P1,P2,P3和P4)的简单例子，其中TP表示可信第3方，设P1选择了P3，那么P1和P3可协商一个随机数R13，然后S1更新为S′1=S1+R13，而S3更新为S′3=S3-R13，P2选择P4生成随机数R24，更新S′2=S2+R24和S′4=S4-R24，P3选择P4生成随机数R34，那么S′3=S3-R13+R34和S′4=S4-R24-R34，最后P4选择P1生成随机数R41，更新S′4=S4-R24-R34+R41和S′1=S1+R13-R41，即：

S′1=S1+R13-R41

S′2=S2+R24

S′3=S3-R13+R34

S′4=S4-R24-R34+R41

显然可见：

∀i,Si≠S′i

S′1+S′2+S′3+S′4=S1+S2+S3+S4

求和，即求平均值(参与人数n已知)显然有众多的实用领域和价值，比如在研究某种疾病，如糖尿病、艾滋病和COVID-19等，研究人员希望获取病人的某个生理指标的平均值，如体温、血压、血糖、身高和体重等，但这涉及到个人隐私，而利用前述方法则可在保护病人隐私的前提下得到这些生理指标平均值，有助于疾病的研究和防治。

(2)求积。

求积方法同前述求和方法类似，区别只在于求积要计算S′i=S′i*Rij和S′j=Sj/Rij，而不是S′i=Si+Rij和S′j=Sj-Rij。如上述4个参与方计算的例子，若此时要求积，那么可执行以下计算：

S′1=S1*R13/R41

S′2=S2*R24

S′3=S3/R13*R34

S′4=S4/R24/R34*R41

则有：

S′1*S′2*S′3*S′4=S1*S2*S3*S4

(3)比较与求距离。

设有2个百万富翁，若要比较他们的财富多少，即哪个更富有，同时又不想公布他们的具体财产，那么，可用一个半可信的TP(Miner)进行如下操作：

步骤12个富翁相互通信来协商一个随机数R，如利用上述的量子QKQ或两方秘钥分发协议；

步骤2然后他们各自对自己的财富值更新如下：S′1=S1+R和S′2=S2+R；

步骤3将更新后的财富值S′i(i=1,2)匿名发送给Miner，例如各自随机选一个Miner计算机的接收端口号来传输；

步骤4Miner可以简单地比较收到的2个值的大小，从而判断出某个端口号的财富值胜出，而无需公布这2个值(若公布这2个值，双方的隐私也能得到部分保护，因为此时双方已知道了对方的财富值，但别人只知道双方的财富差值而不知道各自具体的值是多少或谁更富有)。

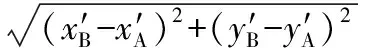
此处虽然以欧氏距离为例进行了说明，但该方法同样可以计算其他方式定义的距离。所以，结合前述平均值可以计算方差，如在疾病研究中计算某个生理指标的方差和概率分布等，这对疾病研究非常重要。另外，在车载互联网中和交通规划之中，利用此方法可在保护隐私的前提下计算车辆之间的距离，从而实现各种基于位置的规划和应用，例如自动驾驶等。基于距离的应用还有很多，比如广告，即当用户靠近某个地方时(在保证其隐私的前提下)向用户手机发送特定广告，还可用于在COVID-19防治中跟踪病例的密切接触者等。

(4)求频繁项。

在频繁项挖掘的应用中，n个参与方利用多方秘钥协商协议[23]来协商一个随机置换σ和一个随机数R，对每种商品的标签index进行如下随机化处理：

index→σ(index)→σ(index)+R

然后把各自的商品/购买次数({index1,index2,…},times)对都发送给Miner，Miner可在本地运行Apriori等算法来挖掘出频繁项后进行公布，这样各个参与者可简单地解码得到真正的频繁项挖掘结果。对Miner来说,收到的数据是经过随机化处理的数据，没有什么意义，从而保证了各个参与方的隐私。

2.2 R-PPDM一般框架

理性隐私保护数据挖掘的框架描述如下(如图2所示)：

(1)参与角色：半可信的数据挖掘方Miner和n个参与方Pi，Pi拥有秘密值Si；

(2)给定一事先约定好的数据挖掘函数f(S1,S2,…,Sn)；

(3)理性假设：假设Miner和各参与方都是理性的。

接下来设计实用的协议安全地计算函数f，计算结果可公布，也可能不公开，仅供Miner做科学研究之用：

(1)针对要计算的数据挖掘函数f，n个参与方相互通信对各自的秘密信息Si进行有限随机化(类似秘密分享)，即各自的Si随机化为S′i，但总体上满足：f(S1,S2,…,Sn)=f(S′1,S′2,…,S′n)；

(2)各方把随机化的S′i发送给Miner，Miner可以通过简单地计算f(S′1,S′2,…,S′n)得到数据挖掘的结果，即函数f(·)的值；

(3)函数f(·)的值对Miner可能有意义(如上述的求和)，也可能无意义(如上述的财富比较)，函数f(·)的值公布之后参与方才能解读。

3 安全性分析

对R-PPDM的安全性分析是基于如下的理性假设和博弈模型：

(1)参与方(即秘密数据拥有者)：

①各参与方希望保护自己的隐私不被泄露，即各自的秘密信息不被其他方获取(可以从挖掘结果中推出的信息除外)；

②在上述前提基础上，各参与方希望Miner能获得预定好的数据挖掘函数的函数值(比如Miner是科研工作者，那么其挖掘研究成果可能推动科学技术进步、预防控制疾病等)。

(2)数据挖掘方Miner：

①希望能获得事先商定好的数据挖掘函数的函数值；

②不与任何一个参与方共谋来试图获取其他参与方的隐私数据(否则曝光后会影响其声誉)；

③可以利用自己收到的数据进行任何的分析、计算来试图获取其他参与方的隐私数据(即使半可信的TP方)。

构建的具体博弈模型如下所示：

参与方为P1,P2,…,Pn,其中,

Pi的可选策略集合为{合作，不合作，合谋};数据挖掘方Miner的策略集为{诚实，合谋}，这里合谋指的是Pi与Miner合作帮助Miner获取他人的隐私数据。

Pi的效用函数值：Up(正确结果)>Up(错误结果)>Up(自己的隐私数据暴露)；Miner的效用函数值：Um(正确结果且获得他人隐私数据)>Um(正确结果)>Um(错误结果)>Um(丑闻曝光名誉受损)。

下面证明在平均意义下策略(合作，合作，…，诚实)为上述博弈(Game)的纳什均衡，假设P1与Miner合谋，即(合谋，合作，…，合谋)，那么对P1来说收益没有变化，而对Miner来说收益提高了，但此时也有行为曝光名誉受损的风险。设曝光概率为30%，并假设Miner的收益为1(结果正确并获得他人隐私)> 0.6(结果正确)> 0(结果错误)>-1(曝光名誉受损)，则其收益的期望值为1*0.7+0.3*(-1)=0.4，小于其诚实而获得的收益0.6。教训就是在实践中，只要对不诚实的Miner的处罚够大，那么就能基本保证不会出现试图偷窃他人数据的行为。其他策略的组合如(不合作，合作，…，诚实),显然双方收益都减少了，所以前述策略为纳什均衡。

但是，如果相关参数发生变化，可能上述策略组合就不是纳什均衡了，具体分析如下：

在作弊和诚实收益固定的情况下，期望收益与被曝光概率的关系如表1所示。

表1中,√标识了行为分界线，曝光的概率小于20%时，Miner的理性选择为作弊，而大于此值其理性选择为诚实。

当曝光概率固定(设为20%)时，惩罚力度与期望收益的关系如表2所示。

表2中,√标识了行为分界线，当惩罚力度小于-1时，Miner的理性选择为作弊，而加大惩罚力度则其理性选择为诚实。

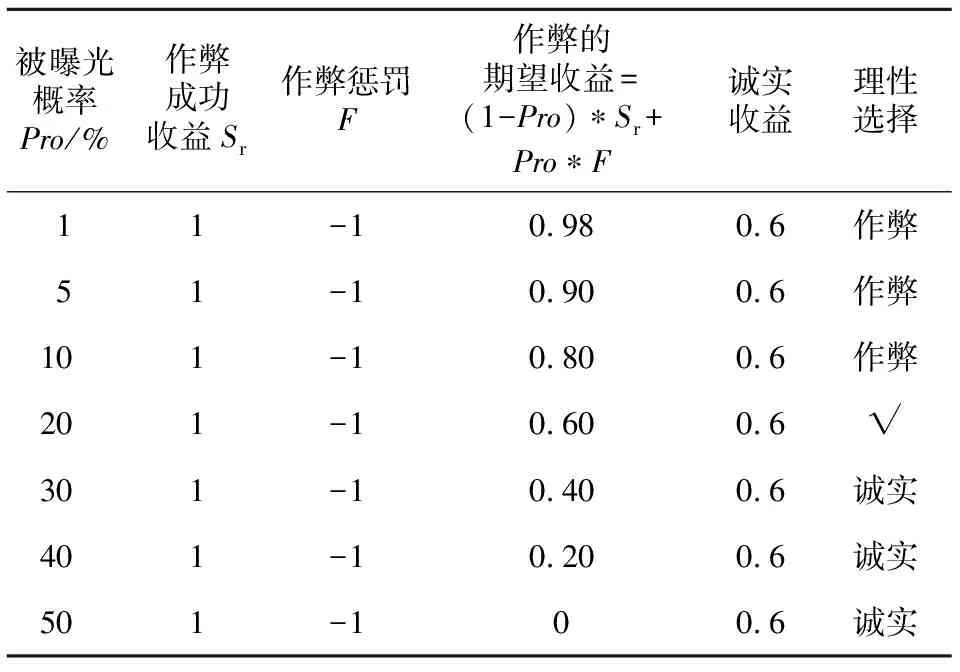
Table 1 Relationship between exposure probability and expected payoff

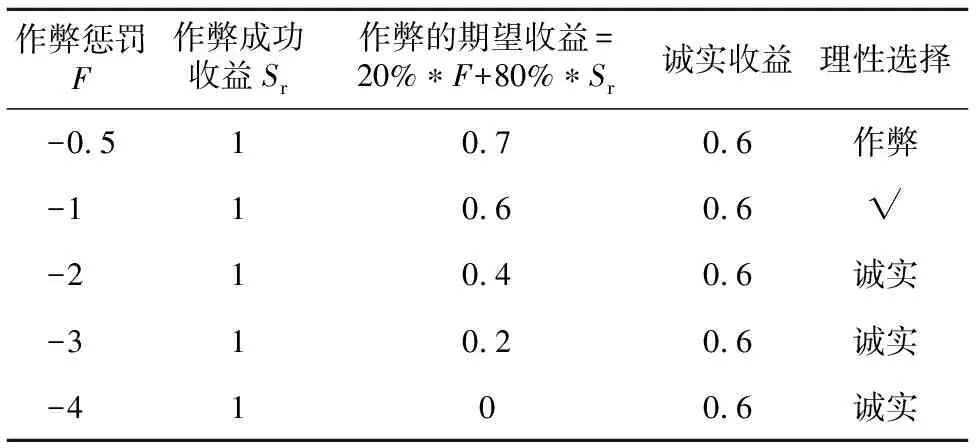
Table 2 Relationship between punishment and expected payoff

由上述分析可知，在实际应用中要根据具体情况设置博弈模型参数，保证诚实和合作为纳什均衡。

下面对前文构建的具体协议进行安全性分析：

(1)求和与求积协议的安全性分析：

①首先对于Miner来说，各参与方发给Miner的数据都是随机值，如Pi发送的是Si+Rij，其中随机数Rij只有参与方Pi和Pj掌握，而根据本文的安全性假设，Miner不会与其他参与方如Pj共谋，所以Miner无法知道Rij，那么他就不可能知道Pi的秘密值Si。

②对任一参与方Pi而言，只将加了随机数的加密数据发送给Miner，不接收任何数据，所以不可能了解他人的秘密数据(除了能够从最终挖掘结果和自身秘密数据推出的数据)；参与方可以提供虚假的数据，但此行为在经典密码学中也不认为是安全威胁，而且本文理性假设各方愿意进行合作并提供真实的数据，以挖掘出真正有价值的信息和知识。

基于上述分析，还可以进一步加强本文求和协议的安全性，原来每个参与方的秘密值Si至少被一个随机值掩盖，因每个参与方Pi都要随机选择另一方Pj生成一个随机数Rij，比如上述例子中的S′2=S2+R24，而有些秘密数据是被几个随机数所掩盖，如上述例子中的S′3=S3-R13+R34；如果一个秘密数据Si只被一个随机值Rij掩盖，Miner只要与Pj同谋得到Rij就可获取秘密数据Si，如前例中Miner只要和P4共谋获取R24就可获取P2的秘密数据S2=S′2-R24；而如果秘密数据被多个随机数掩盖，Miner就要与多个参与方同谋才能获取秘密数据，如前例中若Miner想获取P3的秘密数据S3，那么Miner就要与P1和P42个参与方同时共谋得到R13和R34，才能计算出S3=S′3+R13-R34，即此时秘密数据更安全。由此可以按如下方式来增强安全性：

当第1轮结束后，如果某方发现其秘密数据只被一个随机数掩盖(如上例中的P2)，那么此参与方就重复其在第1轮所做的操作，再随机选择一个其他参与方(同第1轮不同)生成一个随机数对他们各自的秘密数据进行隐藏；所以经过第2轮之后，就能够保证每个参与方的秘密数据都至少被2个以上的随机数掩盖，也即假如Miner想获取某个参与方的秘密数据，那么他必须至少同2个以上的参与方合谋，而且Miner不知道此两方的ID，类似地可以通过增加第三或更多的轮来进一步增强安全性，使得假如Miner若要获取他人隐私数据就要同三方或更多方合谋才行。

(2)对前文中其他协议的安全性分析是类似的。比如对比较协议：Miner通过2个随机的端口收到的是2个随机值，不能得到2个参与方的具体财富值，对Miner而言方程组S′1=S1+R和S′2=S2+R有3个未知数，方程只有2个，也即有无穷多解，即任一R都是可能的解；而2个参与方只是向Miner发送数据和获得公开的最终比较结果(如端口号1161的财富值更高)，不能了解另一方的具体财富值。

4 结束语

本文提出了一种基于理性密码学的分布式隐私保护数据挖掘的框架，同传统经典密码学中的安全多方计算的安全性(即考虑每个成员是完全诚实的或是完全恶意的)相比，本文从实际应用角度、从每个参与方的内在激励动机的角度出发，安全性假设更符合实际，所得出的协议比经典密码学中的安全多方计算的协议效率更高，更适合在实际中应用，并通过具体的例子展示了如何在此框架下构建高效实用的协议。

未来的工作方向：(1)研究更多的数据挖掘函数，直至一般的任意函数，如何在所提框架下实现理性安全计算；(2)如何提升安全性、效率及其均衡性，即根据Miner的可信程度动态调整协议来适应不同的场合；(3)如何引入量子计算、纠缠来提升安全性和效率。