多模态原子力显微镜的空气压膜阻尼效应
2022-10-28黄强先
赵 阳,黄强先
(1. 安徽建筑大学 电子与信息工程学院,安徽 合肥 230601;2. 合肥工业大学 仪器科学与光电工程学院,安徽 合肥 230009)
1 引 言
原子力显微镜(Atomic Force Microscopy,AFM)具有原子尺寸量级的高分辨率,是纳米技术研究的重要工具,被广泛用于纳米尺度成像、测量和操纵等领域[1-7]。AFM 微悬臂工作在轻敲模式时,其探针针尖保持轻敲在试样表面,此时微悬臂与试样表面间距离非常小。在微悬臂的周期性振动过程中,它与试样间隙的气体相应地流入或流出,产生一定的压膜阻尼效应。由于微悬臂对力的敏感传递以及阻尼效应对于悬臂动态特性的影响[8],空气压膜阻尼效应不能被忽略。空气阻尼对微悬臂的动态特性参数有较大影响,从而会进一步影响悬臂的测量特性。
Hoummady 观察到空气压膜阻尼效应的实验现象[9]:当悬臂下方放置和不放置试样时微悬臂的振幅会有一定的偏移;改变微悬臂试样间的距离,其振幅和谐振频率皆会相应地偏移。Gunther 针对扫描探针显微镜中的音叉臂振动中空气阻尼进行了研究[10],将探针末端和被测试样间的阻尼简化为球体和平板间的阻尼模型,分析了振动过程中音叉臂末端的探针和试样间产生的空气阻尼,对于振动过程中音叉臂和试样间的空气阻尼则未做探讨。Leveque,Girard 等结合基于连续梁系统的欧拉-伯努利方程和流体力学理论分析了微悬臂探针低频振动时的空气阻尼效应[11],进而分析了微悬臂受到的大气阻尼效应对振动幅值的影响,而振动过程中阻尼对于阻尼系数和品质因数的影响则未加分析。Zheng Wei 团队进一步分析了不同形状的微悬臂在压膜阻尼影响下品质因数的变化[12]。
以上研究皆为基础谐振模态下压膜阻尼的影响,未考虑压膜阻尼对于微悬臂高阶谐振模态的影响。Ashok Kumar Pandey 仿真了不同阶次谐振模态下微悬臂的空气压膜阻尼系数[13],对于同一悬臂的一阶、二阶、三阶谐振模态下的空气压膜阻尼系数进行实验,结果表明,随着谐振阶次的提高,其空气压膜阻尼对于微悬臂的影响相应减小,品质因数相应增加。但是,其测量的品质因数其实是包含微悬臂振动与大气摩擦所引起的阻尼和压膜阻尼之和,且未对压膜阻尼对于微悬臂振动状态的影响做进一步的研究和分析。
本文基于欧拉-伯努利梁方程和雷诺方程对微悬臂的阻尼效应进行分析,研究基础谐振模态和高阶谐振模态微悬臂的压膜阻尼效应对微悬臂动态特性参数、动态AFM 测量特性的影响,并围绕系统的阻尼效应进行了实验测试。
2 压膜阻尼效应
AFM 微悬臂示意图如图1 所示。矩形悬臂为均质等截面,其长度、宽度和厚度分别为L,b和W,密度为ρ,微悬臂的弹性模量为E,微悬臂的截面面积为A(A=Wb),截面惯性矩为I(I=W3b/12)。

图1 微悬臂-试样简化模型示意图Fig.1 Schematic of simplified cantilever and sample model
由于探针尺寸、质量和微悬臂相比数值微小,故本文忽略探针的作用,将运动的矩形微悬臂简化为矩形平板。忽略惯性效应且不考虑微悬臂在横向的位移,微悬臂和试样间空气压膜效应可用雷诺方程表示为:

其中:x为悬臂长度方向,y为微悬臂宽度方向;p为板间气体压膜压强,μ为气体黏度系数,h为臂与试样间变化的距离,即流体膜的厚度。由于微悬臂振动频率远小于压膜阻尼的中介频率[14],两板间的气体视为不可压缩气体,同时忽略温度变化,可将式(1)简化为:
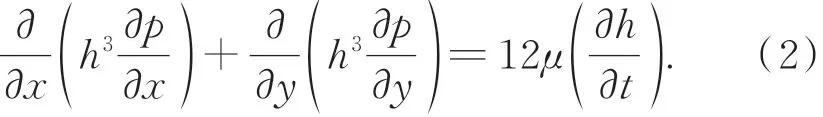
进一步推导出压膜阻尼系数为:

考虑动态AFM 微悬臂在大气环境下振动时,存在着微悬臂振动和大气摩擦产生的能量耗散以及压膜阻尼效应产生的能量耗散。设空气对微悬臂振动导致附加阻尼系数为γair,则分布的外阻尼力为,f(x,t)为微悬臂受到的z向力。微悬臂振动方程为:

其中:

式中:A0为微悬臂振动的振幅值,各阶谐振模态的特征参数αn可由特征方程求出。
设Zi(t)为AFM 微悬臂的第i阶振型,ƞi(t)为相应的广义坐标,则利用振型正交性质,并对所得方程进行解耦[15]可得AFM 悬臂第n阶振动在广义坐标下的微分方程:



式中:cair为微悬臂所受的总阻尼系数,是微悬臂压膜阻尼系数和微悬臂内部能量耗散引起的阻尼系数之和。将一阶谐振模态的α1=1.875,二阶谐振模态的α2=4.694 代入式(9)计算,可得二阶谐振模态和一阶谐振模态微悬臂的阻尼比的关系为:

由此可见,和基础谐振模态相比,处于二阶谐振模态的微悬臂探针,其阻尼比相应地下降,从而减小了阻尼对于微悬臂振动状态的影响。
由于微悬臂工作在近谐振点处,其最大动力位移(即振幅)与静力位移之比为动力放大系数δ,即:

其中γ为微悬臂谐振系统的阻尼比。可见微悬臂的振动幅值由阻尼比决定。在微悬臂和试样接近的过程中,二者距离的改变会导致其阻尼比的变化,进而导致微悬臂振幅的变化。因此,可以通过观察悬臂振幅的变化来观察压膜阻尼的变化情况。
3 实验结果及分析
3.1 实验系统
基于AFM 工作原理,自制了多模态原子力显微镜[16]。该系统可以工作于接触模式、非接触模式,以及轻敲模式。轻敲模式下,系统可工作于基础谐振模态或者高阶谐振模态下。系统示意图如图2 所示。采用具有较高谐振频率的压电陶瓷片励振微悬臂,微悬臂变形检测系统采用光杠杆法检测其Z向变形信息。
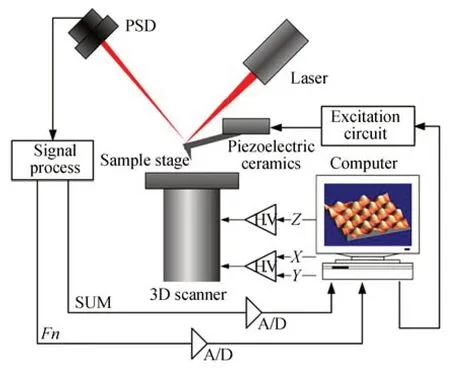
图2 多模态原子力显微镜系统示意图Fig. 2 Functional block diagram of multi-mode AFM
探针-样品逼近系统由远距离逼近系统和近距离逼近系统两部分组成,位于多模态原子力显微镜系统的基座部分。测头及基座部分如图3 所示。远距离逼近系统通过精密微型直流电机驱动螺旋测微头旋转实现探针和试样的大范围、远距离逼近。逼近系统采用千分尺头,可保证逼近过程的平稳性;逼近选用微型直流电机、减速箱减速方式。直流电机通过联轴器与千分尺头相连接,带动千分尺头旋转,沿着导杆的方向上下运动,实现探针针尖与样品台Z方向距离的精密调节。

图3 测头及基座实物Fig.3 Head and base of multi-mode AFM system
近距离逼近系统由封装在基座内部工作台下方的三维压电陶瓷扫描器组成,采用两段单管型压电扫描器控制三维位移量。控制其中一个未四分的压电陶瓷管,分别在其内、外壁施加电压,产生轴向伸缩,从而提供Z向位移,实现探针-试样间距离的小范围、近距离逼近。
3.2 压膜阻尼对悬臂品质因数的影响
选择Budget Sensor 的ContAl 探针,使用公称弹性常数为3 N/m 的微悬臂,微悬臂的几何尺寸(长,宽,高)为225 μm×28 μm×3 μm。激励悬臂工作于一阶谐振模态及二阶谐振模态,一阶谐振频率为82.30 kHz,二阶谐振频率为522.40kHz。保持其他条件不变,仅改变微悬臂-试样间距离,每次距离改变后进行扫频测试,通过幅频特性曲线中的谐振中心频率及半功率带宽计算品质因数。
悬臂与试样间距离控制的具体实现过程为:先给Z向压电陶瓷外壁供120 V 电压,其伸长量约为2 μm;然后,驱动电机转动带动试样工作台逼近悬臂,直至探针近似轻敲至试样表面,此时停止电机,撤去Z向压电陶瓷电压,则探针-试样间距离为2 μm。以此为起始位置,通过给样品台中的Z向压电陶瓷的内外壁施加不同电压使其产生一定的变形量,从而改变微悬臂和试样表面间的距离。
品质因数测量数据如表1 所示。整个测试过程,探针-试样逐渐远离,使用电感测微仪测量其间距离约从2 μm 逐渐增加至10 μm。当探针试样间距离减小时,压膜阻尼效应会导致一阶谐振微悬臂品质因数的明显降低,且随着距离的减小,其压膜阻尼相应增加,品质因数总减小量达到未受压膜阻尼时品质因数的18%。而二阶谐振微悬臂在探针试样间距离减小的过程中,品质因数没有明显的规律性变化。
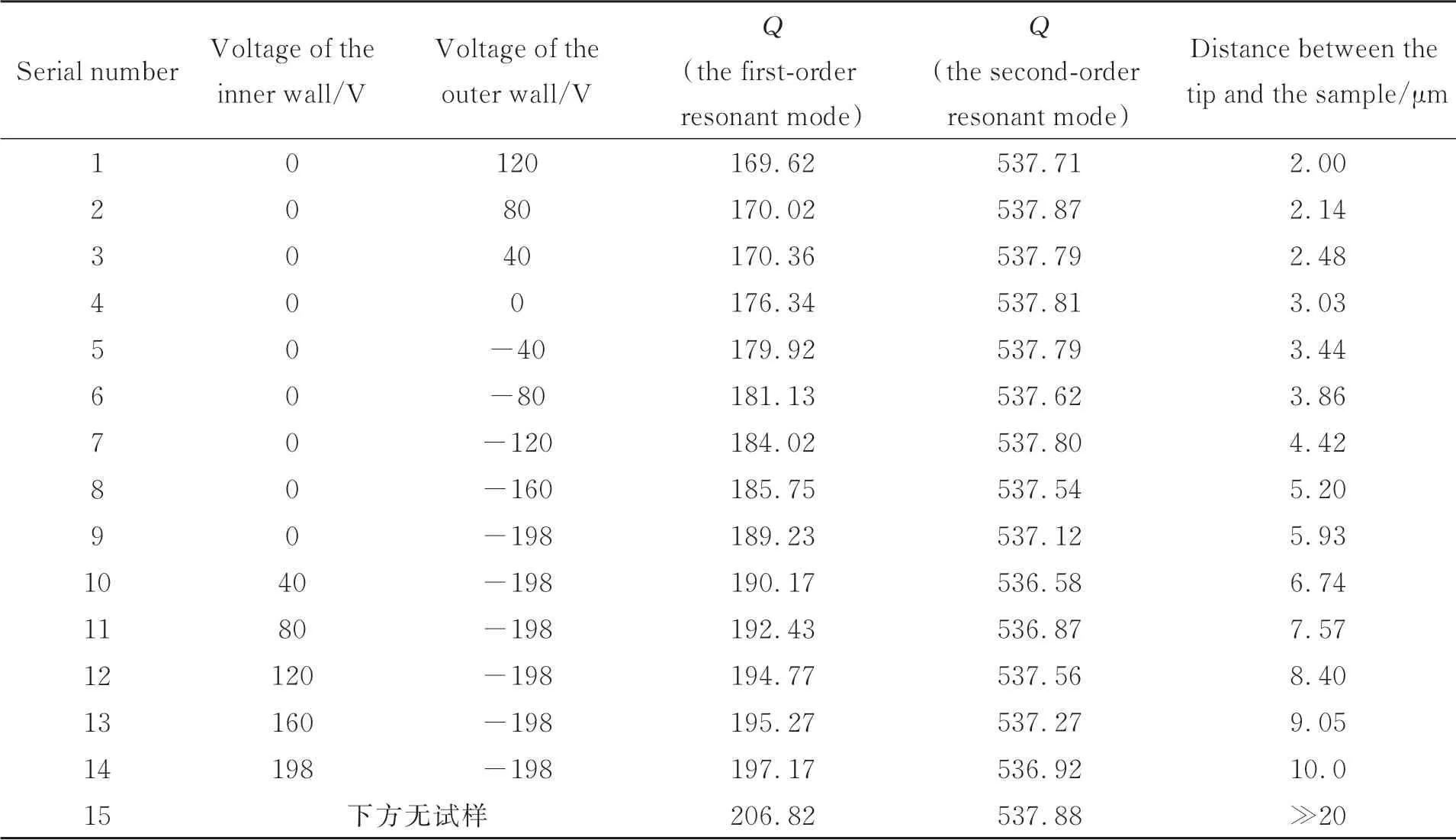
表1 压膜阻尼影响下品质因数测试数据Tab. 1 Test data of quality factor with squeeze film damping
3.3 压膜阻尼效应对AFM 测量特性的影响
3.3.1 基础谐振模态下压膜阻尼效应
在微悬臂与样品间距离为20~2 μm 区间进行了逼近并连续测试悬臂振幅。采用公称弹性常数为0.2 N/m 的探针,几何尺寸(长,宽,高)为450 μm×50 μm×2 μm。使用相同的光强,分别驱动微悬臂工作于接触模式和一阶谐振模态的轻敲模式,测试微悬臂在此范围内向试样表面逼近过程中的力曲线。图4(a)与图4(b)分别为接触模式和轻敲模式下得到的测试曲线。
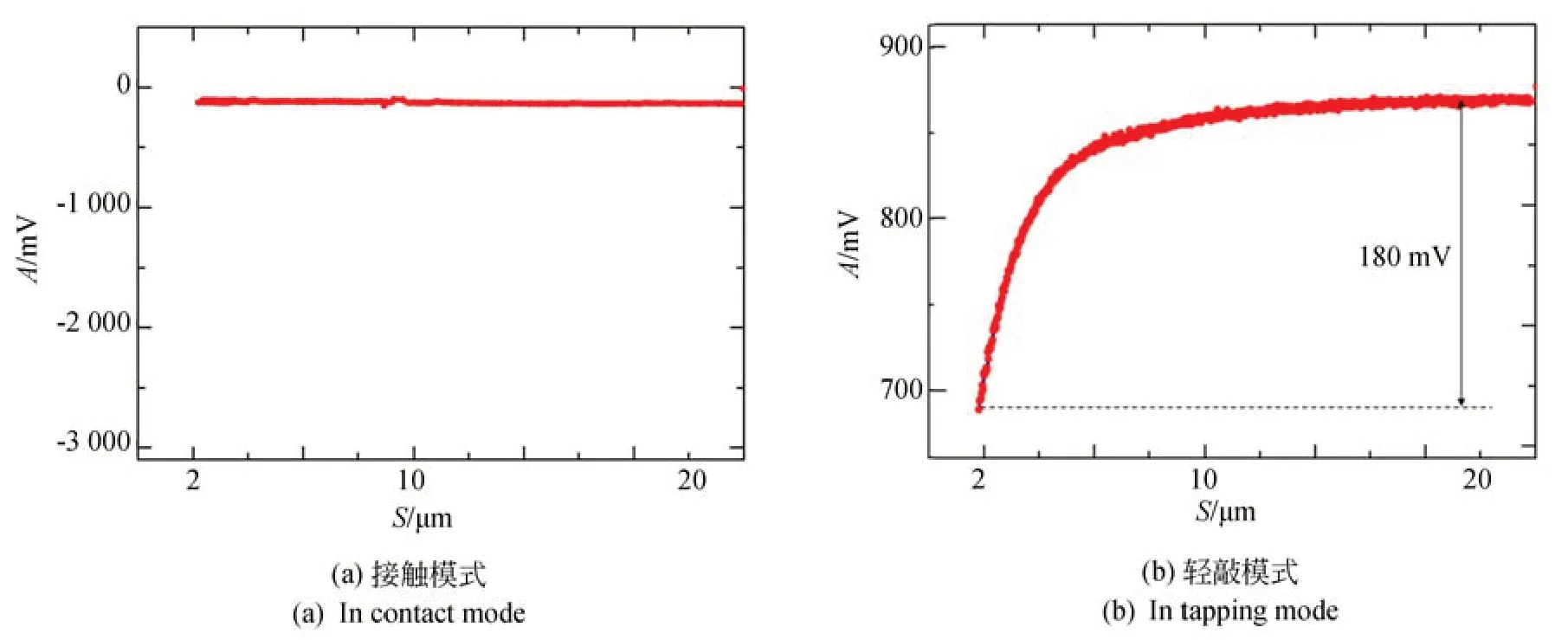
图4 0.2 N/m 悬臂远距离逼近力曲线Fig.4 Approach curves of 0.2 N/m cantilever
在接触模式下,微悬臂无振动,向试样表面靠近,在逼近过程中其偏转量并未发生变化,说明在逼近过程中没有受到外力的作用。而动态轻敲模式下,微悬臂处于近谐振状态,振动频率为15.43 kHz。当微悬臂和试样表面距离较远(大于15 μm)时,逼近过程中微悬臂振动幅值基本不变;当微悬臂和试样表面间距离进一步减小时,微悬臂振动幅值随着微悬臂和试样表面间距离的减小而显著减小。整个逼近过程中振幅减小量约为180 mV,微悬臂自由振幅为870 mV,减小量达到微悬臂自由振幅的20.6%。
由于范德华力的作用区域在1 μm 以内,实验中的微悬臂与试样间距离是超出范德华力作用范围的,接触模式的测试反映了逼近过程中没有其他外力的作用,轻敲模式下逼近过程中微悬臂受到的力应为由于微悬臂振动引起的压膜阻尼力。
实验还使用公称弹性常数为3 N/m 的探针,在相同的实验条件下进行了压膜阻尼特性测试,测试结果如图5(a)所示。

图5 基础谐振模态下3 N/m 悬臂的逼近力曲线Fig.5 Approach curves of 3 N/m cantilever in fundamental resonance mode
从图5(a)可以看到,其逼近力曲线的变化规律和0.2 N/m 微悬臂相同,微悬臂自由振幅为3 250 mV,振幅减小量约为250 mV,约占微悬臂自由振幅的7.8%。进一步进行近距离的力曲线测试,结果如图5(b)所示,可以看到,在微悬臂受到范德华力作用而振幅快速减小之前,随着微悬臂和试样间距离的减小,微悬臂振幅持续减小,减小量约为200 mV。
由实验结果可见,微悬臂处于基础谐振模态下,当针尖距离试样表面较近时(15 μm 以内),微悬臂的振动会产生压膜阻尼效应,随着微悬臂试样间距离的减小,微悬臂的总阻尼系数和阻尼比增加,使微悬臂的动力放大系数减小,进而导致微悬臂振幅相应减小。同时,宽度较大的微悬臂受到的压膜阻尼影响更大,当微悬臂-试样间距离从20 μm 减小到2 μm,宽度为28 μm 的3 N/m微悬臂在接近过程中振幅减小了约7.8%,而宽度为50 μm 的0.2 N/m 微悬臂在接近过程中振幅减小了约20.6%。微悬臂与试样间距离和微悬臂宽度是影响压膜阻尼的主要因素。
3.3.2 高阶谐振模态下压膜阻尼效应
仍使用公称弹性常数为3 N/m 的探针,驱动微悬臂工作于二阶谐振模态,其他实验条件保持和一阶谐振模态实验相同,测试微悬臂逼近力曲线,测试结果如图6 所示。

图6 二阶谐振模态下3 N/m 悬臂的逼近力曲线Fig.6 Approach curve of 3 N/m cantilever in second-order resonant mode
由图6 可知,二阶谐振模态下的微悬臂在20 μm 范围内逼近过程中其幅值并无发生明显的变化,直至它受到范德华力作用而快速减小,说明在逼近过程中几乎没有受到外力的作用。高阶振动模式时,可以克服空气阻尼作用和流体力阻尼作用的交迭,由微悬臂振动过程中引起的空气阻尼作用占主导,而流体力的阻尼作用可以忽略。由此可见,相较于基础谐振模态,高阶谐振模态更有利于轻敲式AFM 减小阻尼对于测试的影响。
AFM 在工作于基础谐振模态下扫描试样形貌测试的过程中,微悬臂和试样间的距离非常小,附加产生的空气压膜阻尼效应则会引起微悬臂所受总阻尼的增加,进而引起微悬臂品质因数的减小。对于AFM 而言,其微悬臂品质因数的减小一方面会导致悬臂最小可探测力梯度的增加,AFM 测量分辨率的降低;另一方面会引起悬臂响应时间的增加,AFM 扫描速度的减小。由此可见,压膜阻尼效应的产生会直接影响悬臂动态特性及AFM 系统的测量特性。
4 结 论
本文对动态AFM 微悬臂的空气压膜阻尼特性进行了研究,分析了影响空气压膜阻尼的因素以及空气压膜阻尼对于AFM 系统测量特性的影响。基于多模态原子力显微镜系统,进行了幅值反馈模式下的基础和高阶谐振模态微悬臂及AFM 系统测量特性的实验研究。测试结果表明,当微悬臂下方有试样且距离较近(10 μm 以内)时,基础谐振模态微悬臂品质因数会由于压膜阻尼的影响而明显降低,且随着微悬臂和试样间距离的减小,其压膜阻尼相应增加,品质因数总减小量达到未受压膜阻尼时品质因数的18%。在微悬臂振幅测试中,所采用的两种微悬臂振幅均有明显减小。当微悬臂-试样间距离从20 μm减小到2 μm,宽度为28 μm 的3 N/m 微悬臂在接近过程中振幅减小了约7.8%,而宽度为50 μm的0.2 N/m 微悬臂在接近过程中振幅减小了约20.6%。可见,微悬臂试样间距离和悬臂宽度是影响压膜阻尼的主要因素。压膜阻尼引起了微悬臂品质因数和振幅的明显下降,并进一步影响悬臂动态特性及AFM 系统测量特性。
在相同的实验条件下,高阶谐振模态微悬臂品质因数及振幅没有发生明显的变化,说明采用高阶谐振模态可以有效地减少压膜阻尼对系统测量特性的影响。本文的研究为进一步研究动态AFM 的阻尼效应提供了理论和实验基础。
