基于随机森林与L-M算法的C4烯烃制备优化模型*

蒋梓浩，任 涛，周 祺，骆加冕

(东北大学软件学院，辽宁 沈阳 110169)

C4 烯烃被广泛应用于化工产品及医药的生产上，乙醇是生产制备C4烯烃的原料.探索乙醇催化偶合制备C4烯烃的工艺条件对实际生产具有非常重要的意义.在制备过程中，有两类问题值得探究：一是不同催化剂组合及温度对乙醇转化率以及C4烯烃选择性的影响；二是如何选择合适的催化剂组合及温度使C4 烯烃收率达到最优值.众多学者对此进行了深入研究：钟思青等[1]使用传统方法，通过热力学计算和建立化学平衡反应体系对乙醇脱水制烯烃过程进行分析；李韶伟等[2]在阿伦尼乌斯方程和灰色关联分析的基础上使用高斯过程回归建立C4烯烃收率的优化模型.为了提高乙醇催化偶合制备C4 烯烃的收率，笔者建立了一个基于随机森林与L-M(Levenberg-Marquardt)算法的C4烯烃制备优化模型，并使用2021年全国大学生数学建模竞赛(CUMCM)赛题提供的实验数据对上述问题进行探究.

1 相关概念与技术

1.1 随机森林算法

随机森林算法通过自助法(bootstrap)重采样技术，从原始训练样本集N中有放回地重复随机抽取K个样本形成新的训练样本集合，然后根据自助样本集生成K个分类树组成随机森林，新数据的分类结果按分类树投票多少形成的分数而定.

随机森林由多个二叉分类树构成，其生成遵循自顶向下的递归分裂原则，从根节点开始依次对训练集进行划分[3].其遵循两种随机性：一是自助法选取训练样本及构建决策树；二是每棵决策树分裂节点处从训练样本集中随机选取特征.

在二叉树中，根节点包含全部训练数据，按照节点纯度最小原则，分裂为左节点和右节点，它们分别包含训练数据的一个子集，按照同样的规则节点继续分裂，直到满足分支停止规则而停止生长．若节点n上的分类数据全部来自于同一类别，则此节点的纯度I(n)=0.

1.2 L-M算法

L-M算法是使用最广泛的非线性最小二乘算法，其结合了梯度下降法和高斯-牛顿法.当梯度下降过快时采用较小的参数，使整个公式接近高斯-牛顿法；当梯度下降过慢时采用较大的参数，使整个公式接近梯度法.L-M算法既具有高斯-牛顿法的局部特性又具有梯度法的全局特性[4]，同时具备优良的数值精度以及稳定性[5].

1.3 粒子群算法

粒子群算法(Particle Swarm Optimization,PSO)的基本概念源于对鸟群觅食行为的研究.通过定义粒子来模拟鸟群中的鸟，粒子具有2个属性：速度和位置.速度代表移动的快慢，位置代表移动的方向.每个粒子单独搜寻其个体最优解，并将结果共享给其他粒子，所有粒子中的最优个体极值作为整个粒子群的当前全局最优解.通过不断迭代，更新速度和位置，最终得到满足终止条件的最优解[6].

2 影响因子重要程度分析

2.1 数据预处理与方差分析

首先，对实验数据进行数据预处理，包括数据清洗和数据标准化处理等.其次，例举出影响乙醇转化率和C4烯烃选择性的影响因子(此处不考虑时间影响因子).通过对实验数据的分析，可以例举出与本研究相关的6种可能的影响因子：温度、Co负载量、Co/SiO2和HAP装料比、乙醇进样量、催化剂质量和装料方式.运用方差分析判断影响因子对乙醇转化率和C4烯烃选择性是否有显著影响.P值是方差分析中衡量控制组与实验组差异大小的指标.若P值低于0.05，认为其对结果具有显著影响，若P值低于0.01，认为其对结果具有非常显著影响[7]，结果远离具有统计学意义.

通过控制变量法，运用Matlab的anova1()函数计算P值，最终结果如表1所示.

表1 各个影响因子P值

由表1可知，装料方式对乙醇转化率、C4烯烃选择性的P值均远大于0.05，说明装料方式对乙醇转化率、C4烯烃选择性均无显著性影响，因此剔除该因子.其余5种影响因子的P值均小于0.05，说明这些因子均显著影响乙醇转化率、C4烯烃选择性.其中，温度对乙醇转化率、C4烯烃选择性的P值小于0.01，说明温度对这两项影响程度高于其余影响因子.

2.2 随机森林模型建立

使用随机森林模型求解乙醇转化率和C4烯烃选择性的影响因子重要程度，具体流程如图1所示.

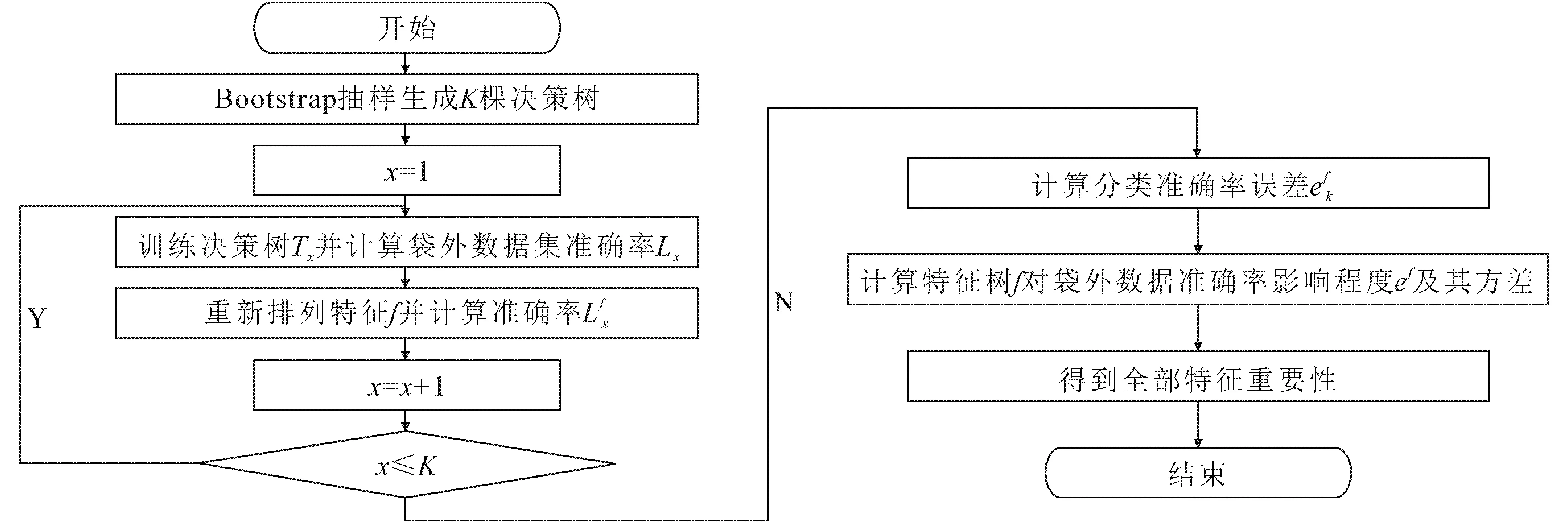
图1 随机森林流程Fig. 1 Random Forest Flow Chart

Step1用Bootstrap方法生成K个训练集，对每一个数据集构造一棵决策树.

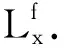
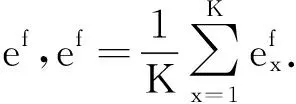
全部特征fw的重要性结果如图2所示.

图2 特征重要性结果Fig. 2 Histogram of Feature Importance

由图2可以看出，各影响因子对乙醇转化率和C4烯烃选择性的重要程度从高到低依次为：温度，催化剂质量，乙醇进样量，Co负载量，装料比.根据目前数据可知，温度变化对催化性能的影响远大于其他指标对于催化性能的影响，而装料比对催化性能影响最小.

3 C4烯烃收率最优值求解

使用L-M算法[9]以及粒子群算法[10]求解C4烯烃收率最优值，具体流程如图3所示.

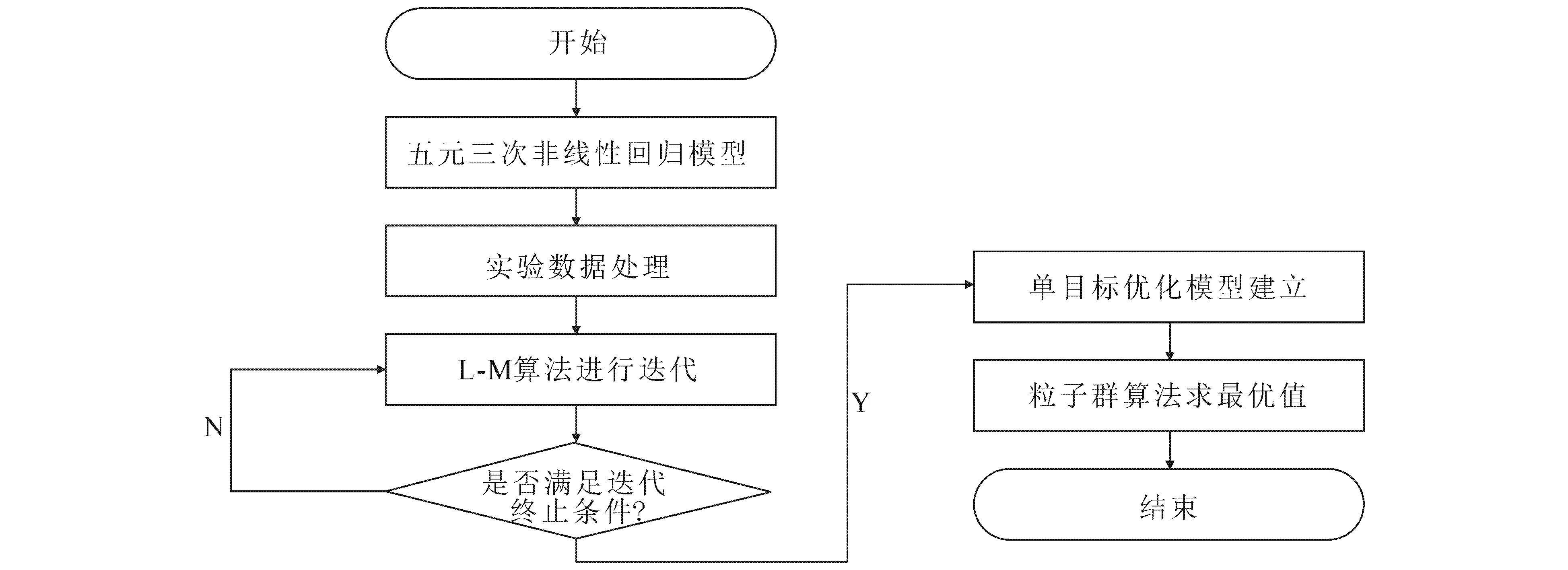
图3 L-M算法与粒子群算法流程Fig. 3 Flow Chart of L-M Algorithm and Particle Swarm Optimization Algorithm

Step1将温度、催化剂质量、乙醇进样量、Co负载量、装料比作为自变量，C4烯烃收率作为因变量,构建关于自变量与因变量的回归模型.回归模型选择五元三次非线性回归模型：

图4 验证集误差分析Fig. 4 Verification Set Error Analysis

Step2剔除催化剂组合编号为A11的石英砂异常实验数据，剩余109组实验数据，其中80%(87组)数据作为训练集用于回归分析，其余20%数据(22组)作为测试集用于回归效果的评估.

Step3设定L-M算法的迭代初始条件为Ai=0，Bi=0，Ci=0，D=0(i=0,1,2,3,4)[11]，迭代终止条件为迭代次数k>100或|zk+1-zk|<0.001.

迭代完成，可得模型的决定系数r2=0.756 9，由图4可知，该模型的拟合效果较好，测试集中的预测值与真实值的误差普遍较小.

Step4根据实验数据的基本约束条件，建立单目标优化模型：

Step5运用粒子群算法求解上述优化模型，C4烯烃收率最优值为42.548 5%，最优值所对应的影响因子值如表2所示.

表2 各个影响因子最优值

4 结语

为提高乙醇偶合制备C4 烯烃过程中的C4烯烃收率，笔者设计了一个基于随机森林与L-M算法的C4烯烃制备优化模型.由模型分析出影响因子重要程度排序为温度、催化剂质量、乙醇进样量、Co负载量、装料比.利用粒子群算法求解出，在理想条件下，C4烯烃最大收率为42.548 5%.结果表明，随机森林算法能准确地分析影响因子的重要程度，L-M算法、粒子群算法对于复杂数据回归求解具有良好的效果，可有效解决优化问题.