基于经典余弦窗三谱线插值FFT的谐波参数估计*

李明皓，汪旭明，张志威，谭宇豪，雷可君

(吉首大学信息科学与工程学院，湖南 吉首 416000)

随着电力电子技术的快速发展，越来越多的非线性负荷应用于电力系统，使得电力系统中产生了大量谐波.谐波不仅对电网的安全运行构成了威胁，也严重影响了电能的质量，所以对谐波进行治理至关重要[1-4].谐波检测是谐波治理的前提，其主要的工作内容是对谐波的幅值、频率及相位等参数进行检测[5-7].目前，快速傅里叶变换(Fast Fourier Transform，FFT)法因原理简单且方便应用，成为电力谐波检测最主要的方法[8].但是，由于电网中的信号多为动态信号，很难对其进行同步采样，因此在利用FFT时会出现频谱泄漏[9-10].此外，信号经过FFT处理后会出现栅栏效应[11-12]，即信号的谱序列为多根离散的谱线，并不能完全反映出原信号的信息，这就会导致信号参数检测时出现误差，从而降低参数检测的精度.在时域给信号加窗可以降低频谱泄漏的影响，在一定程度上提高检测精度，但仍存在修正公式求解复杂的问题.另外，利用传统FFT对谱序列结果修正时仅采用峰值及紧靠峰值处的谱线，并不能很好地抑制栅栏效应的影响[13].针对传统FFT存在的这些不足，笔者拟对信号进行时域加余弦窗截断及频域三谱线插值处理，以减少频谱泄漏和栅栏效应的影响，提高谐波参数检测精度.

1 经典余弦窗及其频域特性

旁瓣峰值电平低及旁瓣衰减速度快的窗函数能够较好地抑制频谱泄露的影响.经典的余弦窗函数具有较好的旁瓣性能，其时域表达式和频域表达式分别为

(1)

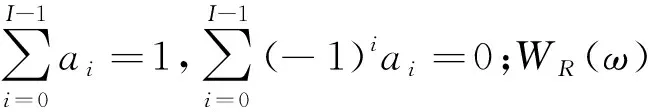
(2)

将(1)式离散化，即令ω=2πk/N，再代入(2)式，可得余弦窗的谱函数

(3)

经典余弦窗函数的系数见表1，表2给出了经典余弦窗函数的主瓣及旁瓣特性.

表1 经典余弦窗函数的系数

表2 经典余弦窗函数的主瓣及旁瓣特性

2 经典余弦窗三谱线插值算法

以采样频率fs对频率为f0、幅值为A0、相位为θ0的连续信号x(t)进行采样，得到离散信号

(4)

其中n=0,1,2,…,N-1，N为采样点数.对(4)式加余弦窗截断后进行离散时间傅里叶变换，可得

(5)

(6)

(7)

因为电网中的信号多为动态信号，所以很难对其同步采样，此时，信号真实频率位置处的谱线k0为频率分辨率的非整数倍，即采样时取不到峰值谱线的位置.为此，结合基于三谱线插值方法来获取峰值谱线k0的位置[15].设峰值谱线k0附近幅值最大的谱线位置为kp，其左右两侧谱线的位置分别为kp-1，kp+1，3条谱线的幅值分别标记为y1=|X(kp-1)|，y2=|X(kp)|，y3=|X(kp+1)|.

在实际应用中，N≫1.(3)式可化简为

(8)

引入参数δ=k0-k，δ∈(-0.5,0.5).当k=kp时，kp-k0=-δ，由(7)式可知

(9)

由(8)式可得

(10)

当k=kp-1时，kp-1-k0=-δ-1，此时

(11)

当k=kp+1时，kp+1-k0=-δ+1，此时

(12)

引入参数

(13)

结合(9)式，并将(10)～(12)式代入(13)式，可得

(14)

由(10)～(12)式可知(14)式是δ的函数，但其形式较复杂，不利于求解出δ.为此，将(14)式记为η=f(δ)，可知其反函数为δ=f-1(η)，此时，令δ在(-0.5,0.5)内取值，利用最小二乘及多项式拟合法可求出δ的表达式.以Blackman窗为例，δ的具体表达式为

δ=0.782 608 64η-0.077 816 42η3+0.016 220 29η5-0.003 728 39η7.

因kp+δ=k0，故可得频率的修正公式

由(7)式可得相位的修正公式

由于kp最靠近真实频点，所包含的信息量也最大，因此在计算时应给予更大的权重，将y1，y2，y3这3条谱线的权重分别设置为1，2，1.由(7)式可得幅值的修正公式

(15)

当N≫1时，(15)式化简为

A0=N-1(y1+2y2+y3)g(δ)，

其中

利用类似于求解δ的方法，可得

g(δ)=1.492 537 30+0.490 447 39δ2+0.087 622 88δ4+0.011 736 62δ6.

同理，可求出其他经典余弦窗函数的三谱线插值修正公式：

(1)Hanning窗：

δ=0.666 666 47η-0.074 061 84η3+0.016 282 44η5-0.003 700 48η7,

g(δ)=1.333 333 31+0.526 581 14δ2+0.117 118 08δ4+0.020 536 63δ6.

(2)Hamming窗：

δ=0.635 293 21η-0.089 969 55η3+0.026 959 09η5-0.007 779 23η7,

g(δ)=1.298 701 27+0.546 636 71δ2+0.128 257 73δ4+0.023 517 84δ6.

(3)Blackman-Harris窗：

δ=0.938 919 01η-0.058 092 48η3+0.003 010 99η5+0.000 397 57η7,

g(δ)=1.658 663 61+0.420 089 40δ2+0.065 093 55δ4+0.007 608 87δ6.

(4) 4项3阶Nuttall窗：

δ=1.014 678 00η-0.035 783 35η3-0.011 088 27η5+0.003 053 83η7,

g(δ)=1.724 338 60+0.383 137 03δ2+0.060 516 43δ4+0.006 663 64δ6.

3 仿真实验

为了验证基于经典余弦窗三谱线插值FFT法的有效性，将其与传统FFT法进行对比实验，其中经典余弦窗为Hanning窗、Hamming窗、Blackman窗、Blackman-Harris窗和4项3阶Nuttall窗.设一个由基波、间谐波和整数次谐波组成的复合信号为

其中：采样频率fs=3 000 Hz；n为采样点数，n=0，1，2,…，N-1，采样长度N=1 024；基波频率f0=50.1 Hz；Am和φm分别为各次谐波的幅值和相位.谐波及间谐波参数的具体设置见表3，仿真实验结果见表4～6.

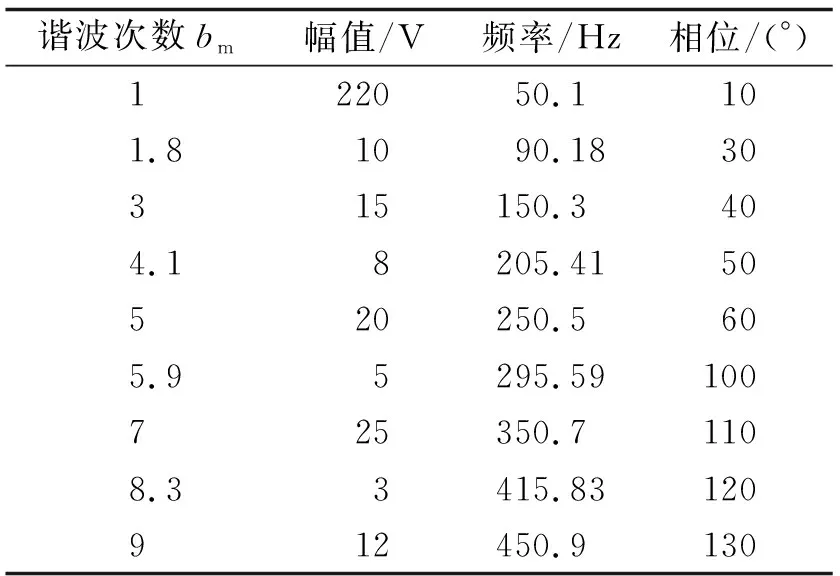
表3 谐波及间谐波参数

表4 谐波及间谐波幅值的相对误差

表5 谐波及间谐波频率的相对误差

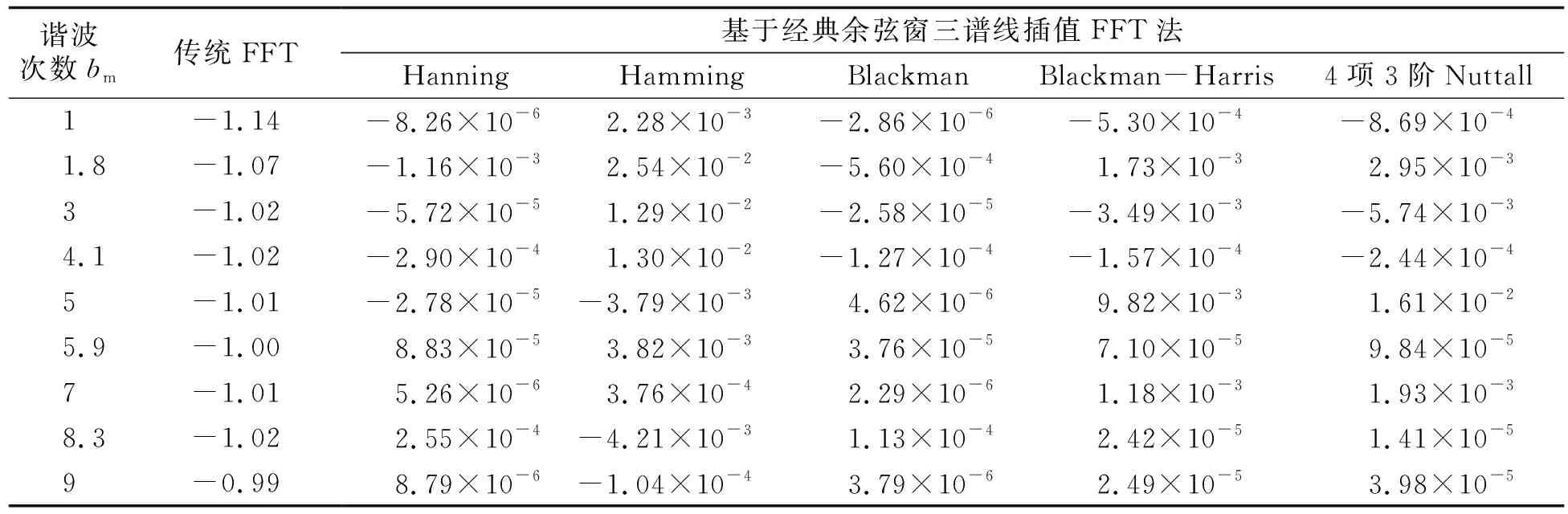
表6 谐波及间谐波相位的相对误差

由表4～6可知：传统FFT法的间谐波与谐波的幅值、频率、相位的检测精度较低，相位的检测误差很大，不满足文献[16]中对谐波测量的要求，且间谐波与谐波之间的频率间隔很近，频谱泄漏会造成很大的影响，如1.8次间谐波和基波，与整数次谐波和整数次谐波相比，1.8次间谐波和基波的间隔更小，所以对间谐波参数的估计不太准确；基于经典余弦窗三谱线插值FFT法，以Blackman窗为例，间谐波与谐波的检测精度均较高，幅值的检测精度相较于传统FFT提高了3～6个数量级，频率的检测精度提高了4～7个数量级，相位的检测精度提高了4～7个数量级，均满足文献[16]中对谐波测量的要求，且虽然也受到间谐波与谐波相隔较近的影响，但能够较好地克服频谱泄漏问题.另外，窗函数的旁瓣性能极大地影响参数检测的精度，但旁瓣性能较好的窗函数未必检测精度就高，检测精度还受主瓣宽度的影响，主瓣宽度较宽的窗函数的检测精度相对较低.

4 结语

提出了一种基于经典余弦窗三谱线插值FFT算法，该算法结合经典余弦窗并利用真实频点附近幅值最大的谱线及其两侧的谱线来减少频谱泄漏和栅栏效应的影响.在此基础上，利用最小二乘及多项式拟合方法推导出谐波幅值、频率及相位的修正公式.对含基波、间谐波与整数次谐波的复合信号进行了仿真实验，结果表明，基于经典余弦窗三谱线插值FFT法相较于传统FFT法具有更高的谐波参数检测精度，能够更好地抑制频谱泄漏和栅栏效应的影响.