基于伽马函数与核熵成分分析的短历时强对流型暴雨设计方法

张 建，和鹏飞，骆进军，周正模

（1.镇江市京口区水利局，江苏镇江 212000；2.黄河水利科学研究院，河南郑州 450003；3.南京市高淳区河道管理所，江苏南京 211300；4.河海大学水文水资源学院，江苏南京 210098）

1 概述

暴雨是城市发生内涝的直接原因，特别是在高度发展的长江三角洲城市群，其地理位置受东亚季风影响，短历时暴雨及强对流事件极易发生，且近年来暴雨强度和频次均有明显上升趋势［1-2］，从而使得城市内涝风险日益加剧［3-4］，严重威胁着城市经济健康发展和人民生命财产安全。国外已有一些学者对城市强对流天气引起的暴雨事件展开了研究，建立了对流型暴雨的识别方法［5］，并分析了对流型暴雨的时间变化特征［6］。国内的相关研究多侧重于强对流暴雨天气的预报或其过程影响［7］，针对强对流型暴雨设计的研究很少。此外，国内目前常用的短历时暴雨设计方法，大多基于暴雨强度-历时-频率曲线编制暴雨强度公式，进而运用芝加哥雨型推求得到短历时设计暴雨过程［8-11］。需要指出的是，芝加哥雨型完全取决于暴雨强度公式，是一种单峰形式的理想化雨型，并未考虑实际暴雨类型上的差异，无法表征强对流型暴雨随时间变化的特征。因此，亟需在深入剖析城市强对流型暴雨特性的基础上，建立可行的城市短历时强对流型暴雨设计方法。

本文选取镇江市为研究区域，在建立短历时强对流型暴雨识别标准的基础上，剖析研究区短历时强对流型暴雨特性，利用双参数伽马函数与核熵成分分析构建短历时强对流型暴雨设计方法并进行可行性检验。研究成果旨在提高人们对城市暴雨特征变化的认识，对镇江市完善防洪排涝系统具有借鉴作用。

2 研究区概况

镇江市属于江苏省地级市，地处北亚热带季风气候，多年平均降水量1 088.2 mm，雨量多集中在汛期5—10月。镇江市暴雨事件多由梅雨锋、中小尺度对流系统、台风或热带系统及其他天气系统（西风带的低槽、切变线等）引起［12］。其中，中小尺度强对流天气引起的短历时强降水具有突发性、局地性强、降水量较大且集中在短时间等特点，在排水不畅的低洼区域极易引起城市内涝灾害。近年来，随着镇江城市化建设进程加快，城市不透水面积比例迅速增长，“热岛效应”与“雨岛效应”现象较为突出，汛期暴雨次数和暴雨集中度均呈增加趋势［13］。城市化进程的加剧与汛期暴雨量的集中导致镇江市区面临着洪涝的威胁，暴雨洪涝灾害事件频发［14］。

3 短历时强对流型暴雨识别

强对流天气引起的天气事件和暴雨事件两者既有联系又有一定的区别，需要根据特定判断标准进行识别。对于短历时强对流型暴雨，国内目前并没有统一的识别标准，因此，本文主要从短历时暴雨和对流特性两方面开展短历时强对流型暴雨的识别。

本文定义短历时暴雨为持续时间不超过3 h且特定时段的最大雨量超过设定阈值的降雨，包含雨强和雨量2个特征参数。参考范兴科等［15］的研究结果，划分短历时暴雨在不同历时时段的标准，如表1所示。本文基于镇江市丹徒站1981—2016年汛期5—10月的逐分钟降水资料，依据独立场次降水事件之间的最小时间间隔为2 h［13］以及表1的暴雨标准，筛选出分辨率为5 min的短历时暴雨事件。

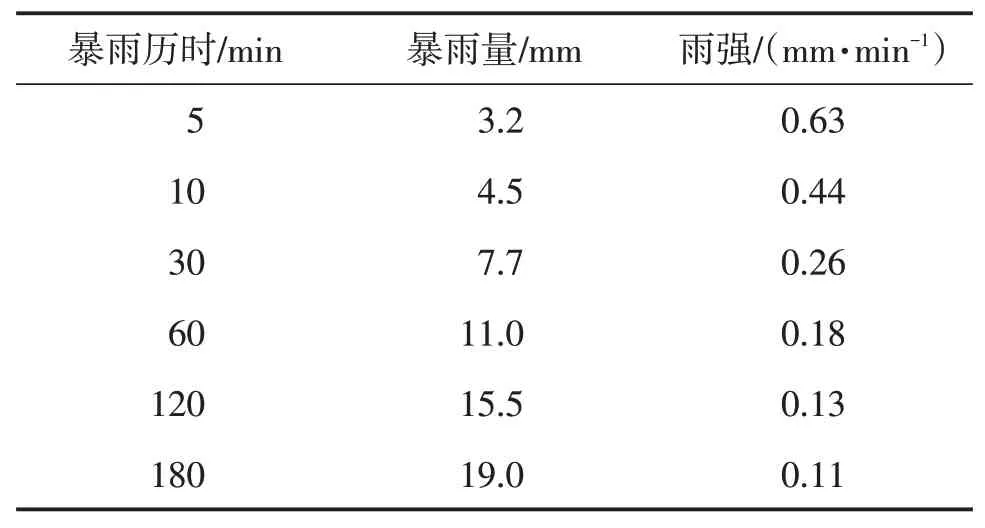
表1 短历时暴雨各时段雨量和雨强评定标准

在筛选出短历时暴雨事件后，进一步判断其是否具有对流特性。Llasat等［5］提出了对流指数β来量化反映一场降水事件的对流程度，当暴雨过程中的最大雨强超过35 mm/h且对流指数β＞0.3时，则认为是一场强对流型暴雨事件。其中，对流指数β的计算公式为

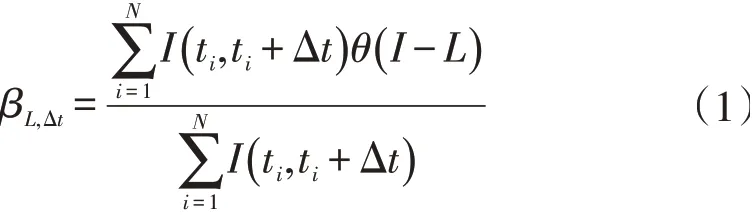
式中：Δt为降水资料的时间分辨率即降雨间隔时段，min；N为暴雨观测数据时间间隔为Δt时的时段个数；I（ti，ti+Δt）为时段ti与ti+Δt的平均降水强度，mm/h，i=1，…，N；当Δt为5 min时，暴雨强度识别阈值L=35 mm/h；θ（I-L）为赫维赛德函数，当I≥L时，θ（I-L）=1，否则为0。

依据此标准，在前面筛选出的短历时暴雨事件中，进一步识别出了57场短历时强对流型暴雨事件，统计值见表2。

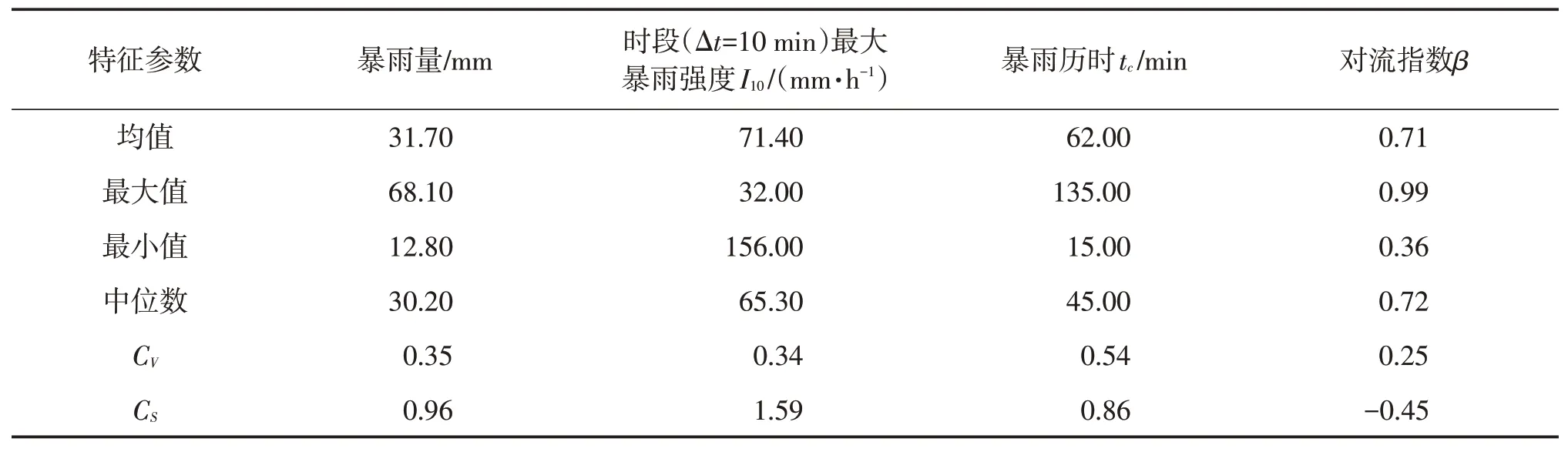
表2 短历时强对流型实测暴雨特征统计

鉴于短历时强对流型暴雨的历时不同，当间隔时段为10 min时，计算累积降水量P与时段最大雨强I10之间的关系，结果如图1所示。

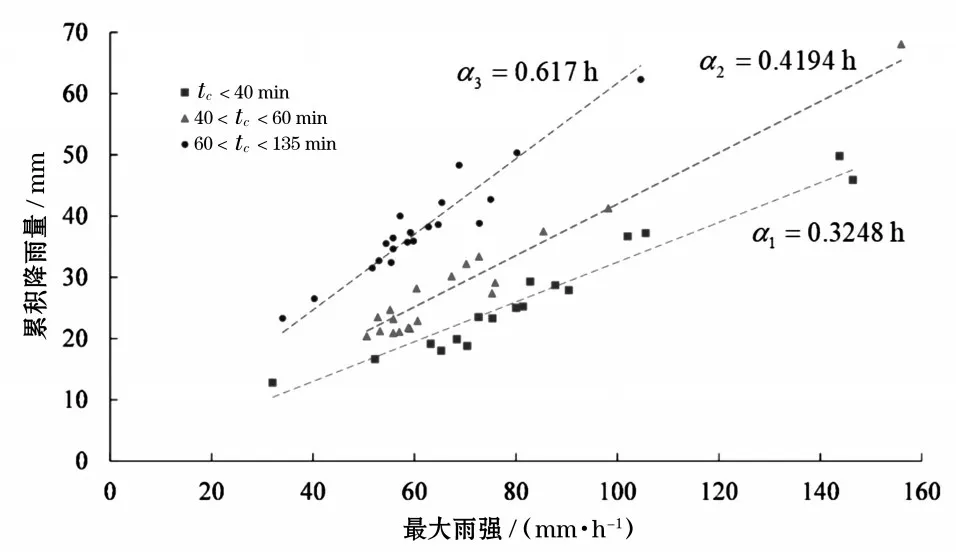
图1 时间间隔为10 min时不同暴雨历时的最大雨强与累积雨量关系

由图1可知，根据累积降水量与时段最大雨强比率的值可将镇江市短历时强对流型暴雨事件分为3类。较低的α值表明暴雨发生的历时较短，暴雨雨强峰值出现的时间较早，较高的α值则说明了暴雨的持续时间较长且累积降雨量相对较大。3类短历时强对流型暴雨的累积降雨量与时段最大雨强的相关系数分别为0.976、0.979、0.914，表明具有很强的相关性。

4 短历时强对流型暴雨设计

4.1 设计原理

暴雨的瞬时强度是随着时间变化而变化的，且这种变化在时间上是连续的，可以用一个连续的数学函数来解释。在此基础上，本文利用双参数伽马类函数来描述暴雨强度的时间变化特征［6］，假设强对流型暴雨持续时间为tc，根据暴雨的实际过程可知tc是一个有限值。因此，为了描述暴雨在有限持续时间内的变化过程，需要对函数f（t）的无穷渐近线采取一个截断准则，当截断水平η确定时，暴雨事件的持续时间tc也就可以通过参数求得。对于不同的截断水平，参数η1和η2的取值范围见表3。

表3 不同截断水平下η1和η2的取值

在一定截断水平下，可以推求出对流型暴雨的总持续时间、累积降水量以及给定时间间隔的最大降水强度，以这些降水特征变量为基础可以完成对流型暴雨的设计过程。

4.2 设计方法

基于统计出的累积降水量与时段最大雨强，对其进行核熵成分分析，建立同时包含累积降水量与时段最大雨强信息的新变量，得到在一定重现期条件下的暴雨量级值。核熵成分分析是在和主成分分析法的基础上引入了“熵”原理，运用非线性处理方法对多降数据进行降维处理，核熵成分分析能最大程度地保留数据的主要信息特征，即使数据维数较低时也能达到较好的降维目的［16］。由于只有累积降水量与时段最大雨强2个变量，且第一核熵成分方差累积贡献量达到87.3%（＞85%），满足要求。第一个核熵成分的计算式为

式中：S（1）为第一个核熵成分值；P为累积降水量，mm；I10为最大雨强，mm/h。

可以用S（1）来描述设计暴雨量级的特征，将S（1）的值分别用3个分布函数皮尔逊Ⅲ型、对数正态、广义极值分布进行拟合，采用线性矩法和K-S检验法进行拟合优度检验，最终确定最优的分布函数F（S（1）），并根据最优分布函数的理论累积概率求出在一定重现期条件下S（1）的值。对S（1）进行理论分布拟合，其结果见表4。

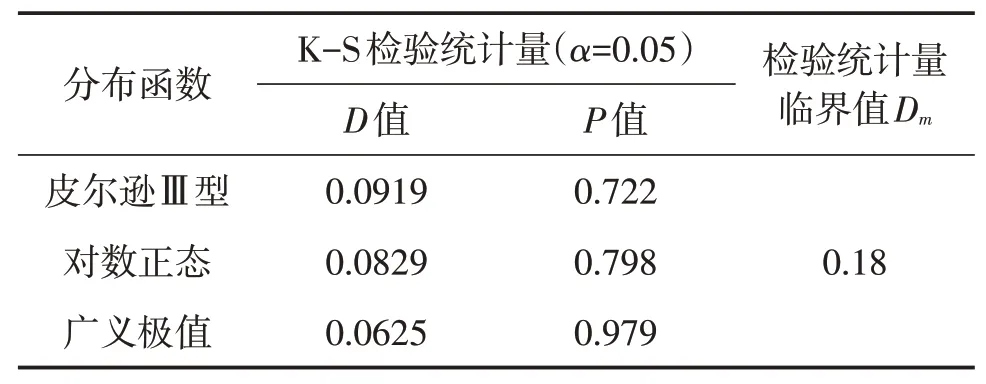
表4 不同分布函数的S(1)拟合结果

由表4可知，3种分布函数都通过了K-S检验，根据P值越大拟合精度越高的原则，可知广义极值分布为S（1）的最优分布函数。

由广义极值分布函数对S（1）的累积分布函数以及经验累积概率值与理论累积概率值的匹配结果，可知广义极值分布函数的经验累积概率值与理论累积概率值拟合效果很好，无论是低值区还是在高值区，经验累积概率值始终都在理论累积概率值附近波动，且距离较近。在求出短历时强对流型设计暴雨的累积降水量P与时段最大雨强I10的基础上，结合短历时强对流型暴雨公式，进而可推求出短历时强对流型设计暴雨过程。

4.3 设计结果

根据镇江市海绵城市建设排水防涝控制标准，短历时强对流型设计暴雨的重现期选取为30年一遇，由计算得到S（1）的值为125.9。结合图1中3类短历时强对流型暴雨的α值，可分别计算出不同类型相应的暴雨参数值P与I10，截断水平η1与时间间隔Δt分别为0.05与10 min，则可计算得到暴雨历时tc与最大雨强位置辅助变量ξ，结果见表5。

由表5可知，α1、α2、α3类型的暴雨累积降水量分别为43.6 mm、52.6 mm、67.9 mm，累积降水量随着暴雨历时的增加而增加，表明设计暴雨量的变化符合实际情况。最大暴雨强度与瞬时最大雨强之间的差异随着暴雨历时的增加而减小，说明短历时强对流型暴雨的对流特性随着时间的增加而减弱，即当历时较短时越容易发生强对流暴雨事件。这也从侧面表明，当镇江市发生高强度对流型暴雨事件时，暴雨的持续时间一般较短，而当暴雨强度较大时，在排水不畅的低洼区域易造成内涝积水。

基于表5参数，可推求出短历时强对流型设计暴雨过程，并与基于暴雨强度公式和芝加哥雨型得到的短历时设计暴雨过程进行对比，其中，α1、α2、α3类型短历时强对流型暴雨分别对应的芝加哥雨型雨峰系数分别为0.5、0.4、0.25，结果见图2与表6。

表5 3种短历时强对流型设计暴雨参数

综合图2与表6可知，对于中短历时的暴雨，2种方法设计的暴雨过程在暴雨发展阶段具有高度的一致性；而对于较长历时的设计暴雨，2种设计方法的暴雨过程在暴雨衰减阶段具有高度的一致性。在暴雨强度方面，芝加哥雨型法设计得到的设计值较伽马类函数设计得到的要大，并且当设计暴雨历时较短时，2种设计方法的最大时段降水强度差距较小，而当历时增加到80 min时，两者的差距明显变大，说明对流型设计暴雨的对流性随历时的增加而减弱，故其最大雨强与芝加哥雨型推求的最大雨强差距越来越大。此外，2种设计暴雨方法推求出的累积降水量也有一定的差异性，在相同重现期条件下，芝加哥雨型的设计雨量要高于对流型的设计雨量，且该差值会随着暴雨历时的延长而不断增大，与最大暴雨强度的对比结果相一致，同样表现出对流型设计暴雨的对流性随历时的增加而减弱。

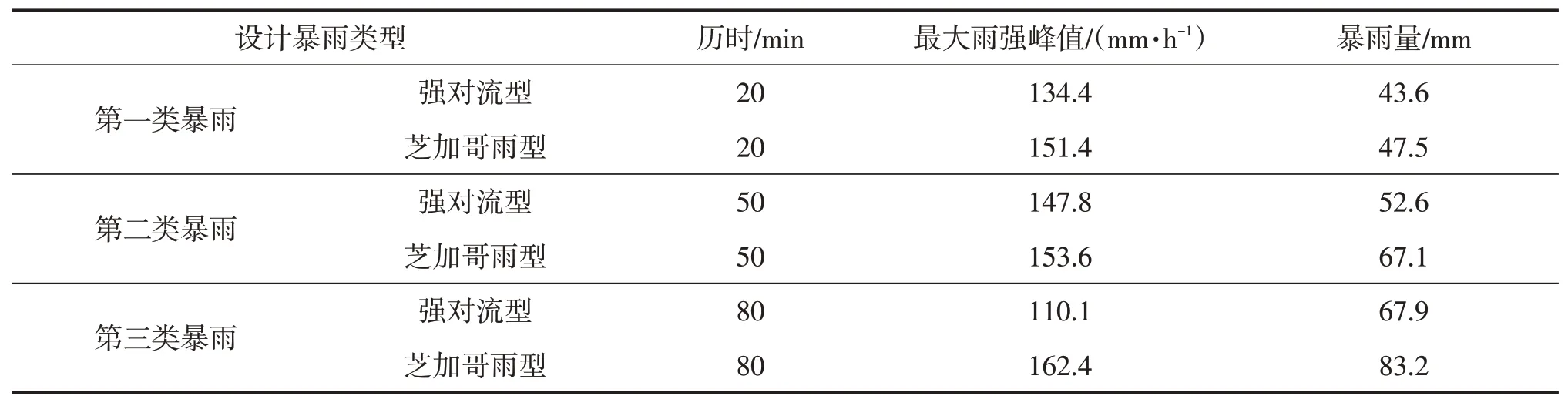
表6 短历时强对流型设计暴雨与芝加哥雨型设计暴雨对比

图2 3类短历时强对流型暴雨与芝加哥雨型设计过程对比

事实上，基于暴雨强度-历时-频率曲线的芝加哥雨型的设计原理是在统计不同降水场次的一定历时时段内最大降水强度的基础上，假设这些不同降水场次在不同历时时段内的最大雨强是同时发生，即使在实际一场降水事件中并没有发生，但芝加哥雨型法将不同降水场次的最大时段降水量综合考虑，最终设计出的是一种复合型设计暴雨。因此，芝加哥雨型是一种最不利的情况，忽略了降水观测资料中实际降水过程，导致推求出的设计暴雨过程无论是在累积雨量上还是在雨峰强度上均会偏高。基于伽马类函数的强对流型设计出的暴雨是基于实际降水事件并从其内部时间结构特征建立起来的，避免了人为地将暴雨发生过程进行复合，推求出的设计暴雨不仅与降水实际过程更接近，而且能反映出暴雨雨强的峰值随时间的变化特征，从而更能精确地反映出实际降水过程中时间变化的多样性特征。

5 结论

本文利用双参数伽马函数与核熵成分分析，提出了一种适用于短历时强对流型暴雨的设计方法，在识别镇江市强对流型实测暴雨事件的基础上，推求了重现期为30年一遇的短历时强对流型设计暴雨过程，并与芝加哥雨型设计结果进行了对比分析。结果表明：根据场次暴雨的时间结构和历时的不同，发现相同重现期条件下强对流型暴雨共有3种不同的类型。推求得到的短历时强对流型设计暴雨过程与芝加哥雨型的设计结果具有较高的一致性，表明提出的短历时强对流型暴雨的设计方法能够满足设计暴雨的时程分配要求，验证了其在实际应用中的可行性，提升了设计暴雨反映区域实际降水过程特征变化多样性的能力。短历时强对流型设计暴雨的雨强和雨量均比芝加哥雨型的小，在暴雨以对流型为主的地区，可用此方法设计排水系统的暴雨标准，使排水工程的设计规模更符合当地实际。