饱和约束下事件触发多智能体系统量化通信环形编队控制
2022-10-28张海江文家燕谢广明景永年
张海江,文家燕*,谢广明,2,景永年
(1.广西科技大学 自动化学院,广西 柳州 545616;2.北京大学 工学院,北京 100871;3.黑芝麻智能科技有限公司,广东 深圳 518005)
0 引言
近年来多智能体的编队控制问题作为一个热点问题被广泛应用于各个领域。环形编队作为编队控制的一个基准问题而备受学者关注。Ⅹu等给出了环形编队的具体定义,并证明了环形编队的可行性。Wang等针对在环形编队过程中的智能体排序和碰撞问题进行分析,设计了相应的通信协议以保证环形编队可实现。
上述控制方法是假设系统中智能体之间的通信信道具有足够大的带宽或容量。但在实际系统中,数字网络通信会受到不同程度的带宽和容量限制。针对这一问题,Frasca 等提出了基于数据量化的通信算法,通过使用静态量化器来完成智能体之间的信息交换。在此基础上,Carli等提出了一种动态编解码量化算法,设计了一种基于编码-解码器的量化器并在量化器中引入一个标度函数,实现了系统在有限量化级别上的一致性。此后,量化算法得到了快速发展,形成了不少理论成果。Li等设计了一种可以对称补偿的量化方法,通过调整量化器自身相应参数,将每个数字通道传输的比特数减少到只有1 bit。
在系统实际工作中,有时无需对系统的控制输入信息进行实时更新,尤其是在某些资源受限的工况下。基于此,Guo 等将事件触发机制引入多智能体系统中,相对于时间驱动机制,这种方法可以有效降低系统的更新频率,减少不必要的通信资源损耗。事件触发机制也被进一步应用于一般线性系统、二阶系统以及非线性系统中。此外,在实际物理系统中存在输入受限的工程约束,这是控制理论面向工程实现所必然要面对的问题。蔡旭等考虑了多智能体系统在实际应用中存在的输入饱和现象,并给出了系统阐述。
综上可知,在多智能体系统研究中,综合考虑输入受限、通信带宽有限和节约有限资源消耗等约束在一起的环形编队控制问题,仍是一个热点、难点问题。为此,本文针对一阶带有输入限制的多智能体动力学模型,围绕耦合考虑系统资源有限、通信带宽限制等问题,提出基于事件触发控制策略和量化通信机制的控制律,在保证系统能实现环形编队的前提下,探究对系统有限资源的节约和通信所需带宽的减小。
1 问题描述
1.1 代数图论
令R、N 和Z分别表示实数集、自然数集和正整数集。表示矩阵的转置,‖‖表示矩阵的范数。列向量1∈R,0∈R表示向量内所有元素分别等于1和0,为自然数。
对于一个加权有向图=(,E,A),其中={,,…,v}表示节点集,={1,2,…,}为节点的下标集。E⊆×表示边集,(v,v)∈E表示智能体到智能体的单向通信信道。 A=[a]∈R 为加权邻接矩阵,如果a≠0则表示智能体与智能体之间存在相应权重的信息交换,a=0则表示智能体与智能体之间不存在信息交换。矩阵=- A为对应拓扑图的Laplace 矩阵,其中矩阵是有向图的度矩阵(为对角阵)。
1.2 环形编队问题描述
考虑由(≥2)个智能体组成的系统,每个智能体都是相互独立的个体。所有智能体的初始位置都随机分布在一个圆上且不发生重合。规定每个智能体只能与其逆时针方向的邻居进行信息交互。
如图1所示,为了更易于解释环形编队的编队运动过程,将按照逆时针方向对所有的智能体从1到(≥2)进行编号,即()=[(),(),…,x()],其中(t)表示智能体在时刻的角度位置状态。所有智能体初始位置均满足如下条件:


图1 智能体在环上分布图
如图1所示,所有的智能体始终都在固定的圆环上运动,且每个智能体仅能感知到逆时针方向邻居的信息;因此,为不失一般性,作如下定义:

其中,为智能体逆时针方向紧邻的智能体,为智能体顺时针方向紧邻的智能体。令d表示智能体与其邻居智能体之间的期望角度间距;因此,期望的环形编队相对间距可以由式(2)的向量确定:

2 系统动力学模型
考虑一个具有输入限制的个智能体组成的多智能体系统,其一阶动力学模型描述如下:

其中,x()为智能体的当前状态,u()为智能体的控制输入。sat(*)为非线性的对称输入饱和函数,其函数表达式为:

令y∈(0,2π)表示智能体与其逆时针方向邻居之间的实际角度距离,其表达式如下:
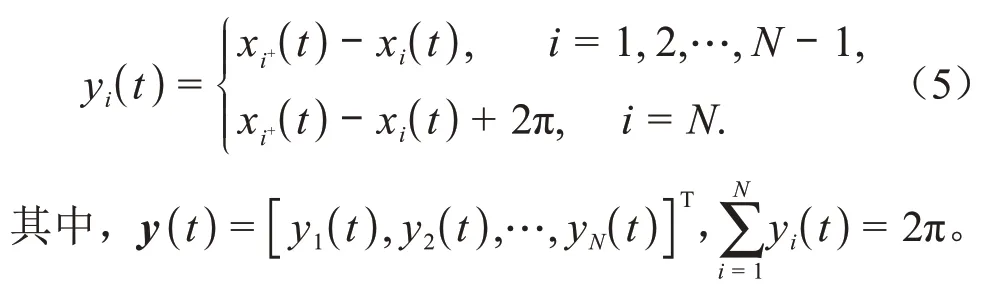
环形编队定义:对于一个给定的可容许的期望环形编队,通过设计分布式控制协议u()=u(y,d),=1,2,…,,使得在满足式(1)的初始条件下,系统(3)的解始终收敛到某个平衡点,且满足=,即可实现环形编队。


其中()表示矩阵I-去掉第一行第一列的一个子矩阵,则有如下关系成立:
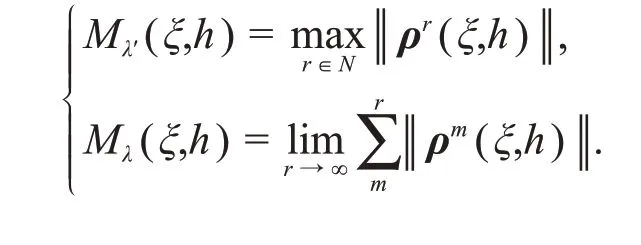
3 基于事件触发与量化通信的控制律设计
首先,借助环形编队控制问题的相关做法,基于事件触发的环形编队控制协议设计如下:






其次,将介绍在有限通信带宽下,多智能体系统中任意2个相邻的智能体间的量化通信的实现过程。对于每个智能体,其中∈{1,2,…,},其对应的基于事件触发编码器φ设计如下:

其中:ξ()∈R 为编码器φ的内部状态;s()为智能体传输给其邻居的当前信息;(-1) >0是一个衰减函数;q()表示具有有限量化级数的均匀量化器,其作用是把智能体当前状态的偏差值映射为离散的量化器所对应的量化层级。q()如下所示:

式中:为量化器的量化间隔;≥1 为量化层级。在每次智能体进行信息传递时,其通信信道的传输比特数为log(2+1)比特。此外,在智能体之间进行信息交换时必须保证量化器始终处于不饱和状态。
当智能体接收到智能体传递过来的当前状态信息s()时,需要通过对应的解码器ψ将智能体的状态值估计出来。解码器ψ数学表达式如下:

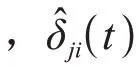
为便于分析,在分布式控制协议(6)的基础上,引入中间变量以简化后续的理论证明,其变换如下:
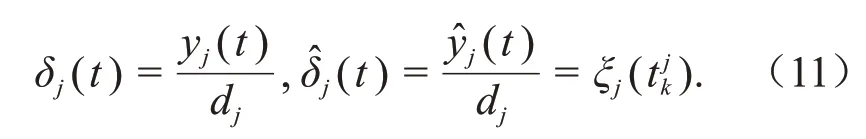
综上设计与分析,联合式(11)、编码器(8)、解码器(10),对控制协议(6)进行设计,可以得到基于事件触发与量化通信机制的分布式控制协议,具体如下:

4 环形编队可实现性与量化器设计合理性分析
4.1 环形编队可实现性理论证明
证明系统在所设计的控制协议(12)的作用下,可以实现期望的环形编队。具体包括2个方面:一是系统在事件触发条件(7)下是稳定的;二是证明系统在前述条件作用下,环形编队可以实现。具体如下:
将式(12)代入式(3),可以得到如下结果:

根据式(13)可以将个智能的系统模型写成紧凑形式,具体如下:

考虑如下合适的Lyapunov函数:

沿着时间变量对Lyapunov函数求导,得到:

令Δ<0,可以得到如下不等式:

根据范数的运算法则可以将式(15)改写为:

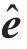
综上,证明了系统在事件触发条件(7)和控制协议(12)下是稳定的。根据文献[15]中的定理1 可知,当时间步长≤1 时,在所给出的控制协议(12)下,可以实现任意一个期望的环形编队。
4.2 量化器设计合理性分析
由于量化器一旦出现饱和则无法确定此时传递的信息是否为智能体的真实状态信息,因此,如何通过合理设计相应参数,保证所设计的量化器在任意时刻都不会饱和是十分必要的。


则基于量化通信的环形编队可以实现,且智能体之间进行信息交互时,量化器始终不会出现饱和。
证明:结合编码-解码器对表达式可以得到:

定义矩阵J= Iξ,其中向量为引理1 中矩阵的第一行,则JL= LJ=0 成立。结合式(18)可得:

为了使证明过程更加清晰明了,将分2个步骤来证明系统工作过程中所有的量化器不会饱和:

由式(23)中的结果可知,当=0 时,系统中所有量化器均不饱和。
2)当≥1,对任意的非负整数=0,1,…,,假定如下关系成立:


在式(26)中,可将复杂关系式分三部分进行整理,具体如下:

结合给出的的存在条件以及式(24)与式(30)可得:

根据式(31)的结果可知,如果存在(2+1)量化电平数的量化器满足式(17)与式(31)的条件时,那么在系统运行的整个过程中,所有智能体对应的量化器都不会出现饱和现象。至此,量化器合理性得证。
5 数值仿真与验证
为验证所提出算法的有效性,本节将给出基于Matlab的数值仿真验证。考虑由6个智能体组成多智能体系统,智能体初始状态为满足条件(1)的任意位置,智能体之间的期望环形编队的角度差由满足条件(2)的向量确定,具体如下:

设定量化器的相关参数为=0.05,=10,=0.982 88。仿真结果如图2、图3所示。
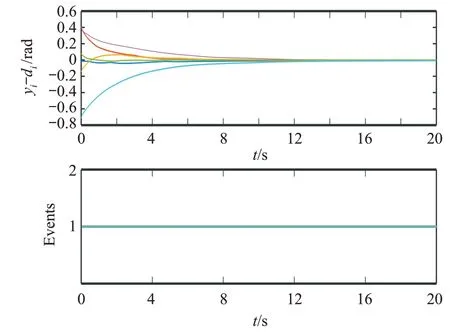
图2 (网络版彩图)连续时间触发下各智能体的状态信息
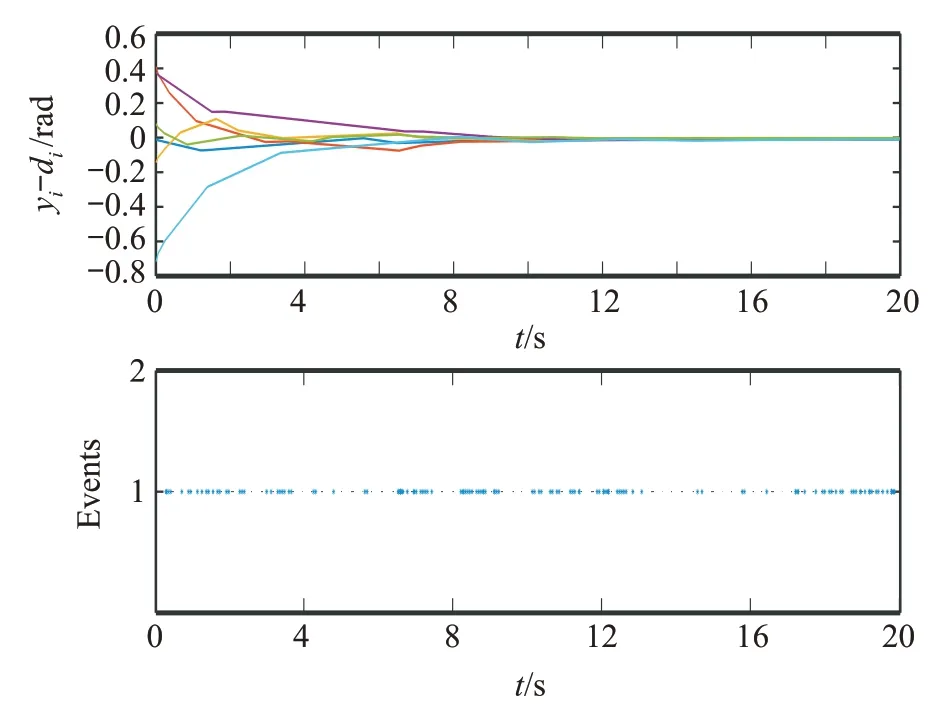
图3 (网络版彩图)事件触发下各智能体的状态信息
通过观察图2 和图3 中的仿真结果可知,在系统允许的误差范围内,事件触发控制策略能有效地降低智能体之间的通信频率,达到节省系统有限通信资源的目的。
本文在文献[16]的研究基础上进一步考虑系统中存在输入饱和限制,结果如图4、图5所示。对比图4 和图5 可以看出,虽然系统中控制器的调节时间会受到输入饱和限制的影响而增加,但系统中的每个智能体都能在所设计的控制协议下使自身状态保持在一个很小的误差范围内,使得多智能体运动至期望编队位置。

图4 (网络版彩图)输入不受限时各智能体的状态信息(详见文献[16])

图5 (网络版彩图)输入受限时各智能体的状态信息
文中设定的量化器量化间隔=0.05。从图6中可以清晰地看到,在系统运行过程中的任意一个时间点上,各个智能体的量化器都没有出现饱和现象,证实了本文所设计的量化通信方案可行。
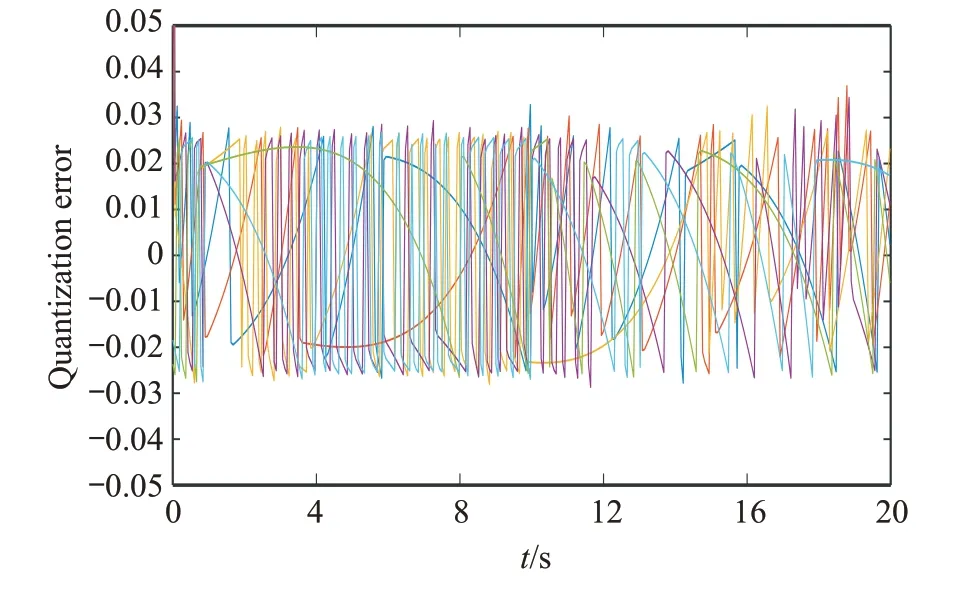
图6 (网络版彩图)各智能体的量化误差(β=0.05)
6 结束语
本文研究了一阶带有输入饱和限制的多智能体系统事件触发量化通信环形编队问题,其中智能体与其邻居之间的通信和状态更新由事件触发机制控制。考虑实际工程中存在输入饱和、系统资源受限和通信带宽受限等问题,设计了带有输入饱和的事件触发机制与量化通信方式相结合的控制策略,在保证任意一个时间点上所有量化器均不饱和的前提下使系统达到期望的环形编队。最后通过仿真验证了所提出控制策略的有效性。未来的工作将更加关注实际系统中的问题,例如将量化通信与输入饱和限制推广到一般线性或者异构系统中。
