地震下深水矩形高墩流固耦合动力响应分析方法对比研究

温 畅 占诗棋 杨 坤 葛书勋

(武汉理工大学交通与物流工程学院 武汉 430063)

大规模的水电资源开发，使得跨越水电站水库的高墩桥梁的桥墩长期淹没在水中。地震作用下，振动的桥墩会受到动水压力影响，这种桥墩-水的耦合作用会放大桥墩的地震响应。因此，在深水桥墩的地震响应分析中必须考虑桥墩-水的耦合效应。

现有的计算桥墩-水耦合效应的主要方法有完全数值法和半解析半数值的动水附加质量法[1-2]。完全数值方法较精确但是计算效率较低，不适合进行大型结构分析。半解析半数值方法避免了求解流体域的复杂过程，采用解析方法求得动水压力之后施加在结构上以考虑流固耦合作用，使得计算效率大大提高[3-4]。基于半经验半理论的Morison方程的附加质量法是计算水中柱体动水压力的常用方法。该方法已被多种抗震设计规范采用，如我国JTG/T 2231-01-2020《公路桥梁抗震设计规范》[5](以下简称《公路规范》)。

目前，关于考虑桥墩-水耦合效应的地震响应计算方法问题，已有很多学者进行了相关研究。庞于涛等[6]采用势流体单元模拟桥墩周围水体并考虑桥墩非线性，研究了动水效应对深水桥梁抗震性能的影响。杨万理等[7]为进一步提高桥梁动水压力计算效率，在ANSYS中开发了附加质量模块，以实现动水压力的界面输入；王丕光等[8-9]推导了任意光滑截面柱体的动水压力解析式,并进一步推导动水附加质量的简化计算公式，使其更加适用于工程实践。但是现有研究中，结合现行规范并考虑墩顶结构附加质量对半解析半数值的桥墩动水附加质量计算方法适用范围进行定量分析的文献较少，在仅有的文献中输入激励时采用的地震波数目也较少，缺乏代表性。

为此，本文以一典型的深水高墩为例，利用有限元分析软件ADINA，建立基于势流体的完全数值模型和基于《公路规范》的动水附加质量模型，对比分析在墩身内外都有水和仅墩身外有水的条件下，考虑墩顶结构质量和不考虑墩顶结构质量的势流体模型和动水附加质量模型的前3阶模态周期变化、振型变化，以及从纵桥向和横桥向输入7条地震动记录时，各模型的墩底最大弯矩、墩底最大剪力和墩顶最大位移的差异变化规律，并以动水附加质量模型与势流体模型的地震响应相对差异为指标，量化它们之间的差异。

1 墩-水流固耦合计算方法

1.1 基于势流体的计算方法

水下结构模态分析可采用基于势的流体单元来模拟结构-水的流固耦合作用[10]。根据流体力学基本理论，势流体为无旋、无黏、无热传递、不可压或轻微可压缩的介质。当流体速度很小时，基于势流体的结构动力特征值问题基本方程如式(1)。

(1)

式中：F(j)=-iφ(j)，其中，φ(j)为流体节点速度势向量；K为结构刚度矩阵；M为结构质量矩阵；U、F分别为结构和流体节点位移列向量；MFF，CFU，KFF分别为势流体的质量、刚度和阻尼矩阵；(KUUs)为由于流固耦合而产生的刚度矩阵；ωj为耦合系统第j阶模态角频率。

进行水下结构的地震响应分析时，结构与水体通过速度势函数与流固耦合边界上对应的结构速度变量相耦合，采用势流体单元的流固耦合动力方程如式(2)。

(2)

1.2 《公路规范》中深水桥墩动水附加质量计算方法

对边长为2ax(m)和2ay(m)且水平地震动输入沿x轴方向的矩形截面桥墩，其附加质量计算方法见式(3)。

(3)

式中：ma为桥墩单位长度水的附加质量，kg/m；ρ为水的质量密度，kg/m3；k为矩形截面附加质量系数，可按表1线性插值求取。

可以看出《公路规范》中的附加质量计算方法是依据Morison方程建立的，并施加了一个修正系数k对结果进行修正。但是Morison方程并没有从理论流体力学的角度被严格证明，其在地震作用下计算动水压力的适用范围也不明确。《公路规范》也只是简单给出了其动水压力计算条文的适用条件是水深在5 m以上，为此，定义量纲一的量参数：水深宽度比C=水深Hw/迎水面宽度a。

研究《公路规范》附加质量计算条文随水深宽度比的变化，进一步分析《公路规范》条文的适用范围。

表1 矩形截面桥墩附加质量系数

1.3 内域水动水附加质量计算

空心桥墩内域水附加质量直接以桥墩内部水的质量为附加质量，内域水高度与外域水相同。得到空心桥墩内域水附加质量的计算方法如式(4)。

min=ρAi

(4)

式中：Ai为空心桥墩内部截面面积。

对于墩内和墩外都有水的情况，将内域水和外域水的附加质量相加，得到空心桥墩的动水附加质量ma，其计算方法见式(5)。

ma=mout+min

(5)

2 数值算例

以某60 m高的等截面矩形空心墩为例，利用ADINA建立桥墩-水耦合系统的完全数值模型，见图1。

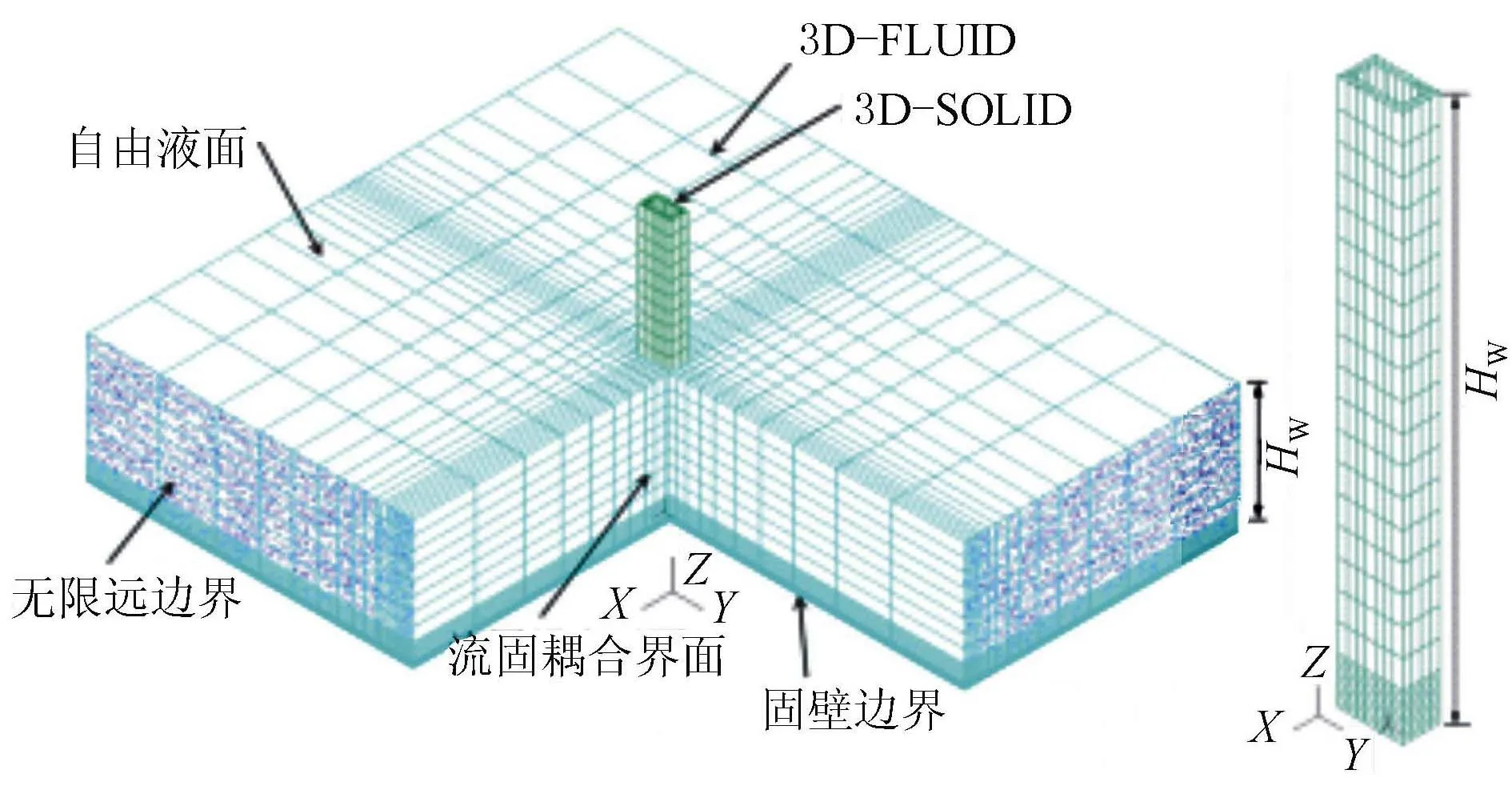
图1 桥墩-水耦合系统数值模型

其中，桥墩外截面尺寸为7 m×4.5 m，壁厚0.8 m，采用8节点三维实体单元对桥墩进行离散，采用8节点势流体单元模拟内域水和外域水，为消除外域水边界的影响，外域水尺寸设置为横截面为70 m×60 m的矩形。假设桥墩墩底固结，墩顶自由；水体无波动，具有理想的无穷远边界，水体表面设为自由液面，四周设为无限远边界，底部为固壁边界；水-结构接触面为流固耦合界面。桥墩材料为C40混凝土，弹性模量为32.5 GPa，泊松比0.2，密度2 500 kg/m3；势流体密度为1 000 kg/m3，体积模量为2.2 GPa。为考虑上部结构质量的影响，墩顶添加集中附加质量，取1 500 t。对于动水附加质量模型，根据公路规范得到的动水附加质量以节点质量的方式赋予水面以下的所有桥墩节点。

此文中针对以下4种工况进行探讨。

工况1，仅考虑空心墩外域水的影响，且不考虑上部结构质量的影响。

工况2，同时考虑空心墩内、外域水的影响，且不考虑上部结构质量的影响。

工况3，仅考虑空心墩外域水的影响，但考虑上部结构质量的影响。

工况4，同时考虑空心墩内、外域水的的影响，但考虑上部结构质量的影响。

水域深度的变化范围为0～54 m,即相对水深为0～0.9,对于工况2、4,假定内、外域水顶面齐平。

3 深水桥墩振动特性比较

为描述结构的振动特性，定义量纲一的量参数如下。

周期增幅RT=(结构有水模态周期Tw-结构无水模态周期T0)/结构无水模态周期T0。

模态周期相对差异ET=(附加质量模型模态周期Tmass-势流体模型模态周期TPBFE)/流体模型模态周期TPBFE。

对建立的势流体模型和附加质量模型进行模态分析，得到不同水位下，2种模型在纵桥向(7 m)和横桥向(4.5 m)的前3阶模态周期变化、模态周期相对差异变化和振型矢量图，见图2～4。由于不同水位和工况下，对应模态的振型形状相似，这里仅列出工况2下纵桥向42 m水深时的振型图，见图4。

图2 模态周期变化

由图2可知，纵桥向和横桥向的前3阶模态周期变化规律类似，但纵桥向模态周期的增幅程度大于横桥向。随着水深的增加，一阶模态周期增幅由大到小依次为工况2《公路规范》模型、工况1《公路规范》模型、工况2势流体模型、工况1势流体模型、工况4《公路规范》模型、工况3《公路规范》模型、工况4势流体模型、工况3势流体模型，说明墩顶结构质量和内水作用对结构的一阶模态周期增幅影响较大；对于二阶和三阶模态周期，工况2条件下的模型与工况4条件下的模型增幅较大，说明内域水的存在对高阶模态的影响较大。

由图3可看出，横桥向公路规范附加质量模型和势流体模型的前3阶模态周期相对差异比纵桥向的小；对于横桥向工况，考虑内、外域水影响的三阶模态周期差异最大，二阶模态周期差异次之，一阶模态周期差异最小，但考虑墩顶质量和内、外域水影响的一阶模态周期差异较小，说明墩顶质量对结构的一阶模态周期影响比内域水对结构的一阶模态周期影响大；对于纵桥向工况，其前3阶模态周期的相对差异变化规律和横桥向类似，但相比横桥向工况，其考虑内、外域水和仅考虑外域水的二阶模态周期相对差异和三阶模态周期相对差异更为接近，说明对于两迎水面尺寸差异较大的结构，在迎水面尺寸较大的方向，内域水对结构的模态周期相对差异的影响较小。

图4 深水桥墩振型矢量图

以上还显示，随着相对水深的增加，纵桥向和横桥向的《公路规范》附加质量模型和势流体模型的前3阶模态周期相对差异逐渐增大，但二阶模态周期相对差异和三阶模态周期相对差异会在特定水位出现增幅突然减小的情况。

4 深水桥墩地震响应比较

从PEER上选取7条典型地震动记录，将峰值加速度PGA统一调整至0.2g，分别沿纵桥向和横桥向输入势流体模型和《公路规范》附加质量模型，进行动力时程分析，阻尼比取为0.05，时间步长取为0.01 s。选取的地震波见表2。

表2 选取的地震波

限于篇幅，这里仅列出3条地震波的时程曲线,见图5。

图5 地震波时程曲线

7条地震波的地震响应相对差异平均值变化，见图6。

图6 7条地震波的地震响应相对差异平均值变化

选取各模型的墩底最大弯矩M、墩底最大剪力Q和墩顶最大位移D作为地震响应的评判指标。定义地震响应的相对差异公式为

(6)

式中：下标mass表示附加质量模型的计算结果，下标PBFE表示势流体模型的计算结果。

由图6可见，考虑纵桥向时，各个工况下墩底最大弯矩的相对差异平均值在各个水位都比较接近，且相对差异平均值在比较接近的水位处达到最大值；墩底最大剪力的相对差异平均值分布类似于墩底最大弯矩，但其相对差异平均值更大，但是在相对水深较大时，同时考虑内外域水影响且不考虑墩顶质量的墩底最大剪力相对差异平均值最大；说明对于不同的地震波，势流体模型和公路规范附加质量模型出现墩底最大弯矩和墩底最大剪力出现阶跃增长的水位比较一致，但是不同的工况对墩底最大弯矩和墩底最大剪力的相对差异平均值影响不大。

对于纵桥向墩顶最大位移，在相对水深大于0.3时，考虑墩顶质量工况的相对差异平均值明显大于不考虑墩顶质量的工况；说明考虑墩顶质量时，《公路规范》附加质量模型计算的墩顶最大位移比较准确。

还可看出，对于横桥向的墩底最大弯矩，各工况差异明显，考虑内、外域水且不考虑墩顶附加质量时，相对差异平均值最大；考虑内、外域水但考虑墩顶附加质量和考虑外水且不考虑墩顶附加质量时，相对差异平均值次之；仅考虑外域水但考虑墩顶质量时，相对差异平均值最小；墩底最大剪力的相对差异平均值变化类似于墩底最大弯矩，但相对差异平均值峰值出现的水位有所不同；说明对于横桥向工况，当仅考虑外域水但考虑墩顶质量时，《公路规范》附加质量模型计算的墩底最大弯矩和墩底最大剪力比较准确。

对于横桥向的墩顶最大位移，其相对差异平均值变化类似于墩底最大弯矩。

综合对比纵桥向(7 m)和横桥向(4.5 m)地震响应，可以看出，迎水截面尺寸较小的横桥向地震响应相对差异平均值较小，且墩顶附加质量和内、外域水对地震响应的影响较为明显。还可看出，以墩底最大弯矩和墩底最大剪力作为地震响应的评价指标时，存在响应指标阶跃增长的问题，且势流体模型和公路规范附加质量模型出现阶跃增长的水位不一致。

5 结语

通过建立基于势流体的完全数值模型，对比分析通过公路规范建立的动水附加质量模型，就深水矩形空心高墩的前3阶模态周期、振型和其墩底最大弯矩、墩底最大剪力和墩顶最大位移的结果进行了比较。结论如下。

1) 在有水的条件下，《公路规范》附加质量模型和势流体模型的前3阶模态周期相对差异随着水深的增加而增加，但仅考虑外域水和墩顶质量影响且迎水面尺寸较小的结构的前3阶模态周期相对差异值最小。

2) 相比二阶和三阶模态周期，《公路规范》模型计算的横桥向和纵桥向的一阶模态周期的相对差异值较小。

3) 在有水的条件下，仅考虑墩顶质量和外域水影响且迎水面尺寸较小的结构的墩底最大弯矩、墩底最大剪力和墩顶最大位移的相对差异值都较小。

4) 《公路规范》附加质量模型和势流体模型的墩底最大剪力相对差异值比墩底最大弯矩和墩顶最大位移的相对差异值大。

5) 综合考虑7条地震波对应的地震响应结果时，《公路规范》模型计算的墩底最大弯矩、墩底最大剪力和墩顶最大位移都偏大。