基于人工蜂群算法的灌区水资源优化配置方法

李旭杰，穆营利，吉拥平，孙 颖，黄凤辰

（1．南通河海大学海洋与近海工程研究院，江苏 南通 226300；2．河海大学计算机与信息学院，江苏 南京 211100；3．中国科学院上海微系统与信息技术研究所无线传感网与通信重点实验室，上海 200050；4．钛能科技股份有限公司，江苏 南京 211806；5．江苏开放大学信息工程学院，江苏 南京 210017）

0 引言

节水灌溉的有效利用奠定了我国农业发展的基础，是粮食安全的保证。截至 2019年，我国的灌溉面积已经达到了7400万hm2，其中耕地灌溉面积大约占全国耕地面积的 1/2，灌区的有效利用大幅度提高了粮食产量[1]。然而，由于灌溉过程中对地下水开采和使用的不合理，导致出现地下水水位下降和地表沉降现象，造成作物产量下降、生态环境破坏、生态多样性消失等不可逆转的结果[2]。纵观国内外研究，已有学者对水资源优化配置进行了探索。Georgiou 等[3]以农业总收入最大化为目标，建立了多种作物的灌溉分配模型，并采用模拟退火算法对模型进行求解。但此研究仅考虑到不同作物的灌溉面积及灌溉水资源分配，缺乏对地表水与地下水优化配置的研究，并且模拟退火算法收敛速度较慢，其算法性能易受到多种因素的影响，稳定性较差。Nezhad 等[4]创建了一个优化灌溉用水的模型，通过修改作物响应因子值，以得到最小化产量估计值，从而有效提高了相对用水效率。Khosrojerdi等[5]利用隶属函数的两阶段随机模糊规划方法，对不同用户进行水资源优化分配。Mousavi 等[6]以灌区总效益最大化为目标，将灌溉水深量及其种植面积作为决策变量，采用鲸鱼算法对模型进行求解，但鲸鱼算法容易陷入局部极值，且收敛速度较慢。国内相关研究虽然起步较晚，但也有一定的成果。姚斌等[7]建立了多目标水资源联合调度模型，并采用目标规划法对模型进行求解，得到了在不同保证率下灌区地表水和地下水联合调度方案及农作物种植面积，然而此研究并没有考虑有效降雨量和作物需水量，且目标规划算法收敛效果不佳，易陷入局部最优解。虎海燕[8]以灌区内作物种植分配为决策变量建立了种植结构模型，在现有水资源分配的基础上得出灌区科学合理的种植结构比例，但此研究未考虑灌区水资源的优化配置。赵敏等[9]针对内蒙古河套灌区严重缺水的问题，考虑土壤水分平衡，建立了灌溉水资源优化配置模型，研究了在不同的地下水及土壤含水量情景下水资源优化配置的方案，并利用 Lingo 软件编程求解模型，但此模型只对单一作物具有可行性，不能够广泛应用。钱瑞秋[10]以甘肃疏勒河流域灌区为研究区域，建立了水资源优化配置模型，采用粒子群算法对模型进行求解，求得灌区不同作物的用水量，但粒子群算法具有陷入局部极值的劣势。耿金荣[11]基于富南灌区提出采用井渠结合的灌溉方式，对地表水与地下水资源进行联合调度，然而此研究仅凭经验对水资源进行配置，未对调度进行详细建模，准确度不高。

基于江苏省宿迁市皂河灌区，以灌区效益最大化为目标，综合考虑作物需水量与有效降雨量，采用人工蜂群算法对灌溉地下水资源与地表水资源配比进行联合优化，该算法控制参数少，收敛速度快。结果表明，采用该方法，地下水与地表水的配比更加合理，能有效促进水资源的可持续发展。

1 模型的建立

1.1 目标函数

灌区水资源优化配置主要考虑每种作物地下水和地表水灌溉的最佳水量分配。本研究充分考虑作物需水量及有效降雨量，以灌区经济效益最大化为目标，建立如下数学模型：

式中：F为灌区的总经济效益；j为第j种作物种类；Cj为第j种作物的价格；Aj为第j种作物的种植面积；Yj为第j种作物的单位面积产量；Wjs为地表水供给作物j的量；cw为地表水的单位成本；cg为地下水的单位成本；ETj为第j种作物的灌溉需水量；J为作物种类的数量。

1.2 约束条件

在对式（1）进行优化配置时需满足如下约束条件：

1）可供地表水量约束条件。供给每种作物的地表水量的总和应小于等于可供地表水总量，约束条件可表示为

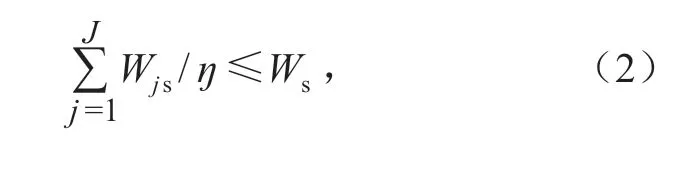
式中：Ws为可供地表水总量；ŋ为灌溉水资源利用率。

2）可供地下水量约束条件。供给每种作物的地下水量的总和应小于等于可供地下水总量，约束条件可表示为

式中：Wjg为地下水供给作物j的量；Wg为可供地下水总量。

3）水量平衡约束条件。每种作物的灌溉用水量应等于作物需水量减去有效降雨量，约束条件可表示为

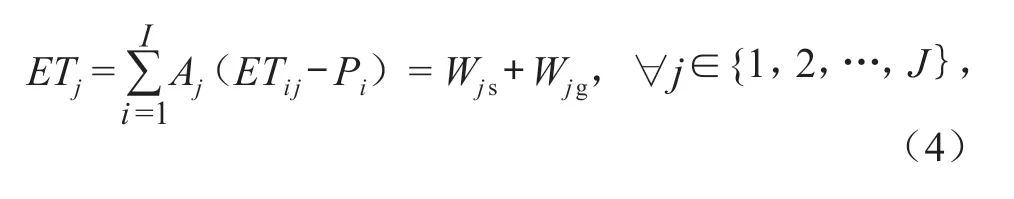
式中：ETi j为第i个月作物j的单位面积需水量；Pi为第i个月的有效降雨量；I表示月份数，取I= 12。因为ETi j和Pi为常数，所以有以下公式

即Aj可由Wjs和Wjg得出，但需同时满足约束条件 4）和 5）。

4）作物种植面积约束条件。所有作物的种植面积之和应小于等于可种植作物总面积，为保证粮经比（粮食作物和经济作物之比），每种作物的种植面积都要限制在一定种植面积内，约束条件可表示为

式中：A为可种植作物总面积；Ajmax为第j种作物可种植的最大面积；Ajmin为第j种作物可种植的最小面积。

5）水资源总量约束条件。所有作物总共的灌溉用水量应小于等于可供地表水量与可供地下水量的和，约束条件为

2 模型的求解

2.1 人工蜂群算法

人工蜂群算法是由 Karaboga 于 2005年提出的一种基于群智能的全局优化算法，其思想来源于蜂群的采蜜行为，蜜蜂根据各自的分工进行活动，并实现蜂群信息的共享和交流，从而寻找问题的最优解[12]。人工蜂群算法中，每个蜜源的位置代表了待求问题的一个可行解，蜂群分为采蜜蜂、观察蜂和侦查蜂。采蜜蜂与待求目标函数的可行解对应，一个采蜜蜂对应一个蜜源；观察蜂则按一定的概率选择要跟随的采蜜蜂，去寻找对应目标函数的可行解；侦查蜂则自由地搜索目标函数的可行解[13-16]。

2.2 基于人工蜂群算法的灌区水资源优化配置方法

本研究提出基于人工蜂群算法的灌区水资源优化配置方法，具体步骤如下：

1）初始化算法参数。人工蜂群算法的种群大小影响着算法的收敛效果，一般情况下种群规模越大，算法性能会越好，算法收敛速度也会越快，但计算复杂度会增加。人工蜂群算法探索能力较强，在一定种群规模下即可有效收敛到最优值。设控制参数L为同一个解可被搜索到的最大次数，当该解的搜索次数达到L时，则把该可行解附近寻找的采蜜蜂转变为侦查蜂，侦查蜂继续寻找新的可行解。该控制参数关系到算法的全局搜索能力，参数较小时，算法随机性强，有利于避免陷入局部极值，但收敛速度较慢；参数较大时，算法收敛较快，但易陷入局部极值。综合考虑算法的搜索能力和计算复杂度，设置种群规模N=200个，控制参数L=10 次，最大迭代次数Tmax=200次，初始化迭代次数T= 0。

2）编码及初始化。采用序号编码方式对种群进行编码，定义N个目标函数的可能解。设种群中第k个个体（蜜蜂）对应的第j种作物的种植面积为Ak j（k= 1，2，…，N；j= 1，2，…，J），分配的地表水量为Wk js，分配的地下水量为Wk jg。Wk js，Wk jg初始值的计算公式如下：

根据约束条件 3），可得Ak j的初始值为

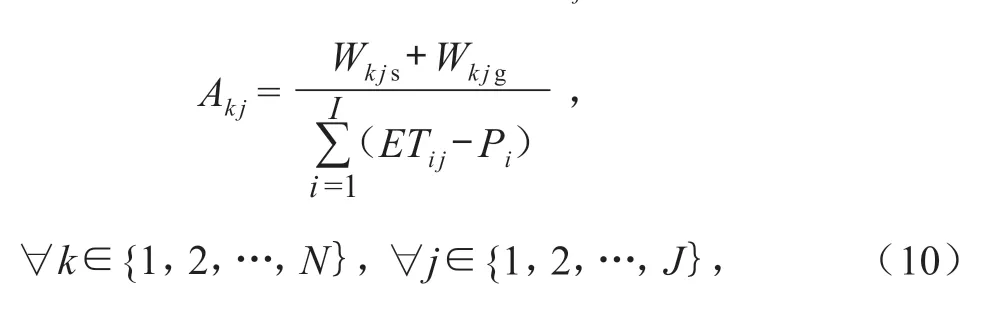
式中：Wjsmax和Wjsmin是第j个作物分配地表水量的上下界；Wjgmax和Wjgmin是第j个作物分配地下水量的上下界；rand [0，1] 是取值 [0，1] 范围的随机数。

为保证解的有效性，需验证Wk jg，Wk js，Ak j是否满足约束条件，若满足则完成初始化，若不满足，则对变量Wk jg，Wk js，Ak j进行重新赋值。

3）计算适应度函数值。定义适应度函数为

根据式（11）求解种群中所有N个蜜蜂的适应度函数，根据适应度函数值的大小，将蜜蜂分为采蜜蜂和观察蜂 2种，适应度值较大的前一半为采蜜蜂，后一半为观察蜂。

4）采蜜蜂阶段。每只采蜜蜂根据迭代搜索公式寻找最优解并保留当前最大值，搜索公式如下：

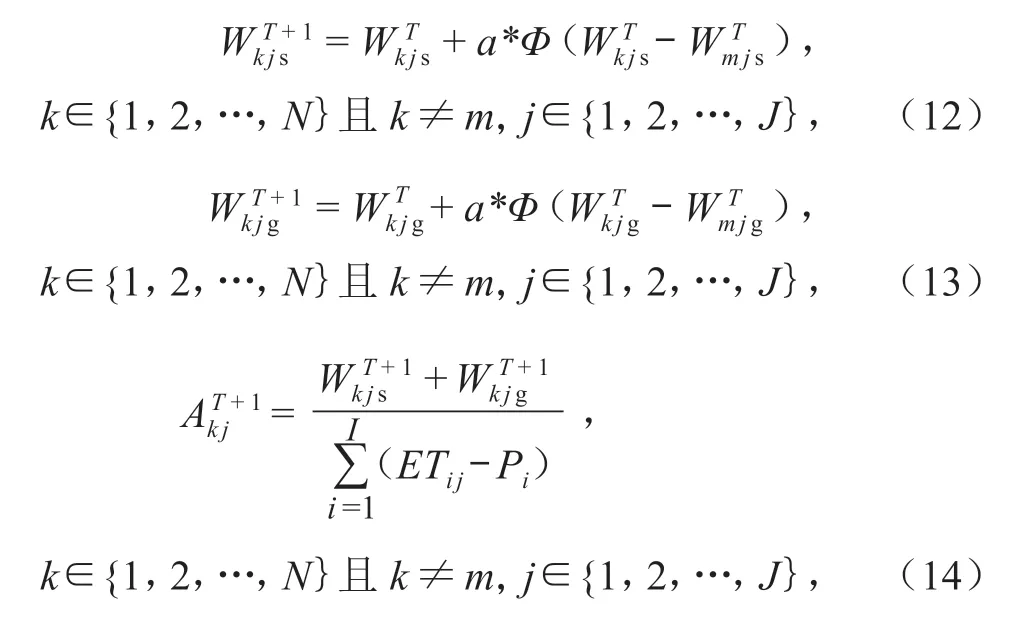
定义搜索次数记录变量l（k），表示同一个解被搜索到的次数。若搜索得到的新解对应目标函数值优于原解的目标函数值，则用新解替代原解，令其对应的l（k）= 0；否则，更新l（k），使l（k）=l（k）+1。为保证解的有效性，需验证，是否满足约束条件，若满足则完成初始化，不满足则对变量进行重新迭代赋值。

5）观察蜂阶段。观察蜂按照轮盘赌的方式选择对应的函数解，Pk表示观察蜂选择第k个采蜜蜂对应函数解的概率：

式中：fk表示第k个采蜜蜂对应函数解的目标函数值，选择当前函数解后，观察蜂按照步骤 4）的迭代公式在当前解附近进行邻域搜索，若新搜索到的目标函数值比当前解的目标函数值更优，则替代该函数解，同时更新对应的l（k）。

6）侦查蜂阶段。搜索过程中，如果某个解经过L次迭代搜索后还没有寻找到更优的解，则该解就会被放弃。侦查蜂则尝试寻找一个新解，侦查蜂寻找新的目标函数解的搜索公式为：

7）将当前迭代次数T增加 1，若当前迭代次数T小于最大迭代次数Tmax，则返回步骤 4）反复迭代，直至达到最大迭代次数Tmax。

人工蜂群具体算法流程如图1所示。

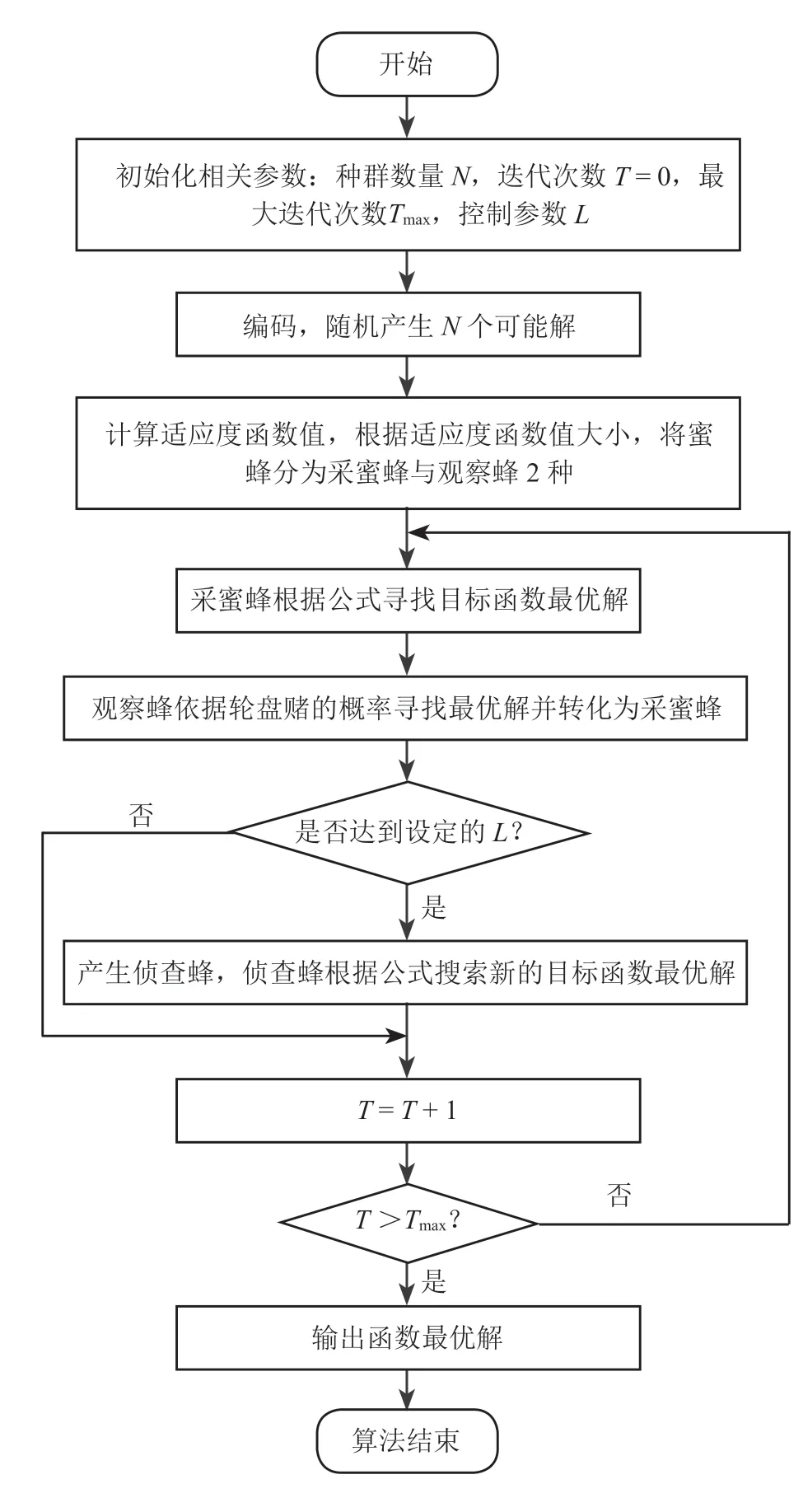
图1 人工蜂群算法流程图

3 实例运用与分析

3.1 研究区概况

皂河灌区位于江苏省宿迁市的西北部，北靠骆马湖和京杭大运河，西与徐州市睢宁县毗邻，西北与邳州市接壤。灌区位于暖温带季风气候区，气候温和，四季分明，多年平均气温为14℃，日照时间为2271h，年降水量在1000mm 上下，且分布不均，大都集中在 6—8月，灌区地表水供水量为2.1 亿 m3，地下水年开采量为 700万m3，地表水价格为 0.3元/m3，地下水价格为 0.8元/ m3。灌区总面积为 2.34万hm2，灌溉水利用系数为 0.83。

灌区作物基本信息如表1所示。将表1 作物基本信息数据代入所提算法的目标函数及约束条件中，对目标函数进行优化求解。

表1 作物基本信息表

第i个月的有效降雨量Pi一般采用经验的降雨有效利用系数公式进行计算[17]：

式中：Pi'为月降雨量；a为降雨有效利用系数。当Pi'＜50mm 时，a= 1；当Pi'在 50～150 mm 之间时，a= 0.8；当Pi'＞150mm 时，a= 0.7。灌区平均有效降雨量年内分配情况如表2所示。

作物潜在蒸腾量通常使用 Hargreaves-Samani 公式进行计算[18]：

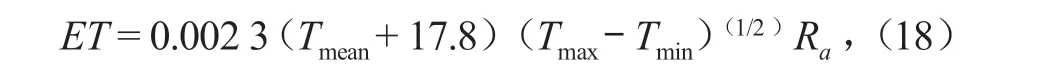
式中：ET为潜在蒸腾量；Tmean为日平均气温；Tmax为日最高气温；Tmin为日最低气温；Ra为总的太阳辐射。

作物需水量是作物在给定环境条件下正常生长所需的水量，计算公式如下：

式中：ETc为作物需水量；Kc为作物蒸腾系数，其中小麦、玉米、水稻、棉花的作物蒸腾系数取值分别为 1.27，0.83，1.20，0.92。

根据式（19）得出灌区主要作物需水量情况如表3所示。由表2 有效降雨量数据和表3 作物需水量数据可以得到作物的灌溉用水量。

表2 多年平均降雨量年内分配 mm

表3 不同作物 1—12月需水量 m3/ hm2

3.2 优化配水结果与分析

采用粒子群和人工蜂群算法对灌区水资源进行优化配置，如图2所示。从图2 可见，基于人工蜂群算法的灌区水资源优化配置方法相比基于粒子群算法的优化配置方法具有更快的迭代收敛速度和更优的配置结果。与粒子群算法容易陷入局部最优相比，人工蜂群算法具有更强的全局搜索能力，因此所得的水资源配置结果也更优。

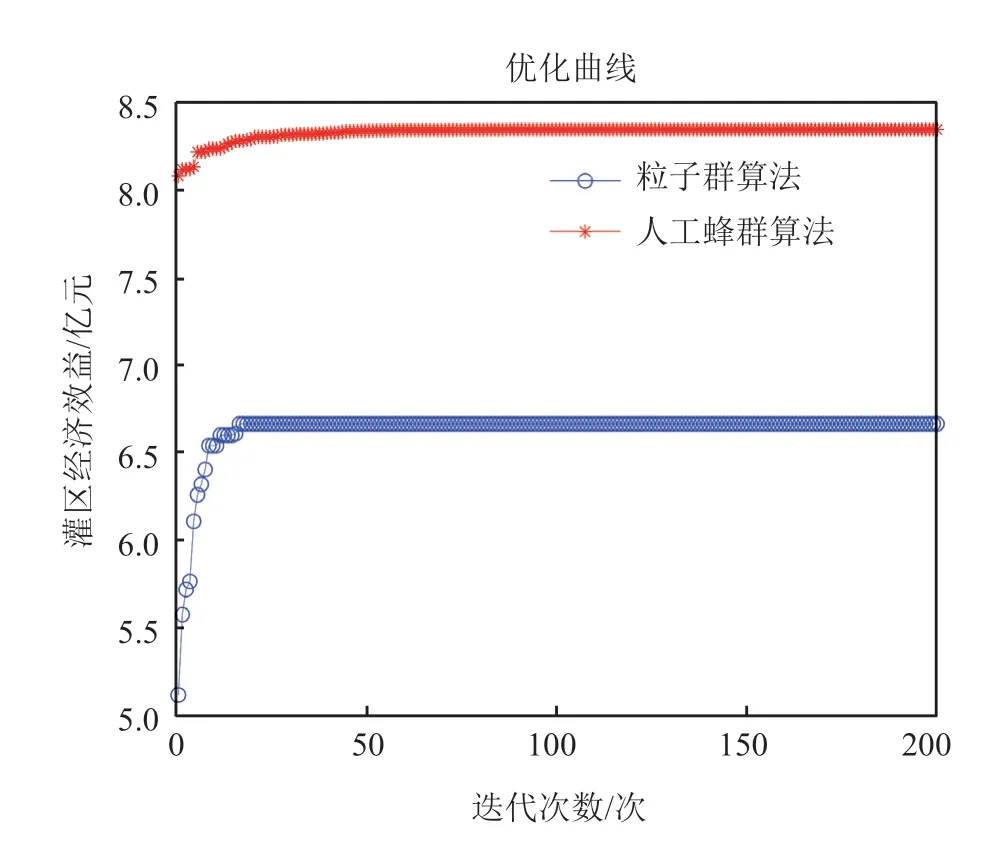
图2 2种算法优化过程示意图

基于所提算法，优化后灌区经济效益约为8.33 亿元，地表水量和地下水量的优化分配结果如表4所示。优化后各种作物的种植面积分配情况如表5所示。由表1 可得传统经验配水方式下灌区作物用水总量约为 8000万m3。由表4 数据可以看出：优化后的灌区总用水量约为 7000万m3，比传统经验配水方法的用水量减少约 1000万m3，且用水量主要来自地表水，减少对地下水的过度开采。同时，作物种植结构也得到优化调整，主要种植作物为小麦和水稻轮作，在此基础上可种植少量的需水量较少且经济效益高的棉花和玉米作物，从而使灌区经济效益达到最大化。

表4 不同作物 1—12月需水量万m3

表5 作物种植面积优化结果 万 hm2

对所提算法的配水结果、基于粒子群算法的优化配水结果和实际需水结果进行了比较，如图3所示。从图3 可见：基于人工蜂群算法的优化配水过程与灌区作物需水过程相对一致，而基于粒子群算法的配水过程则偏差较大，也再次验证了所提算法可有效提高灌溉水资源利用率。

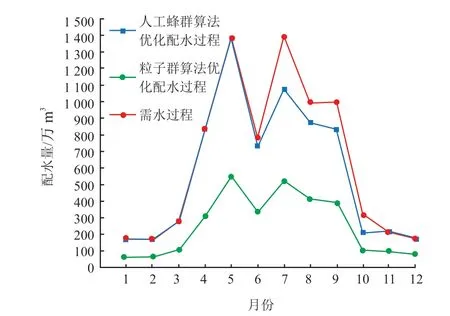
图3 优化配水与需水过程图

4 结语

以灌区经济效益最大化为目标，充分考虑灌区有效降雨量与作物需水量，提出基于人工蜂群算法的灌区水资源优化配置方法。和遗传算法相比，人工蜂群算法收敛速度快，全局搜索能力强，能快速有效地得出灌区灌溉地表水与地下水的优化分配。优化配水后的结果表明：相比传统经验式配水方法，所提的灌区水资源优化配置方法可使灌区经济效益达到 8.33 亿元，有效提高了灌区经济效益，灌溉总用水量减少约 1000万m3，提升了水资源的利用率，且用水量主要来自地表水，灌区作物水资源分配情况更加合理，同时灌区的作物种植结构也得以改善。灌区水资源优化配置方法可在各灌区进行推广，具有普适性。本研究优化模型的目标仅考虑了灌区经济效益，未来可综合考虑社会和生态效益等多种因素，建立多目标模型对水资源进行全方位的优化配置。