GPS高程拟合在水利测量中的应用研究

张浩然

（济宁市黄淮水利勘测设计院，山东 济宁 272000）

0 引言

水利工程是关系国计民生的重大项目，在经济快速发展的今天，我国水利工程已由零起步，并逐步适应经济社会体制的改革与发展，水利行业的管理监督体制也日益健全和完善[1-4]。但目前一些水利工程测量还采用传统的水平测量法，耗费大量物力、财力、人力。GPS 是一种应用在测绘、导航、天文、通信等诸多领域的测控技术，具有自动、快速、准确等特点。GPS 高程测量技术广泛应用于工程建设的全过程，可提高工程的工作效率，所以研究 GPS 高程测量技术在水利水电工程中的应用势在必行[5-8]。

因水利工程项目的设计、施工、竣工验收，以及安全运营检测与环境监测阶段都需要准确及时的高精度测量结果，所以国内专家对此进行了大量研究，将 GPS 高程分析应用于水利工程中，解决传统仪器测量误差较高的问题。但 GPS 高程测量为大地高，与我国现行的标准高程体系有很大不同，需将大地高转换为正常高，但转换过程中会出现高程异常，因此需采用拟合方程对已知的高程进行异常处理。由于高程拟合过程中会出现误差现象，目前有多种拟合公式，但适用于水利工程的拟合方法却不太多。彭光林[9]通过对水利测绘发展现状的研究发现，GPS 高程拟合过程中，控制网测量、平面拟合、曲面拟合和精度评测是产生误差并影响精度的主要原因。阴学军[10]研究了 GPS 高程测量在水利水电工程中的应用，发现只需要采用合理的数据处理模型，便可满足常规生产的需要。贺圆圆等[11]研究了拟合方程在工程测量中的应用，并提出高程拟合中需要注意的有关问题。综上所述，本研究对 GPS 高程测量技术在水利工程测量领域中的应用进行高程精度拟合研究，寻找适用水利测量方面的拟合方法，以更好地服务于水利工程建设。

1 常见高程系统

1.1 常见高程系统类型

1.1.1 大地高系统

大地高是一个几何数字，没有任何物理上的意义。大地高是地球点沿参考椭球面法线至参考椭球面的距离，用H表示。

1.1.2 正高系统

正高系统指从地球某一点上的铅垂线到地球水准面的直线距离，用Hg表示。正高的物理意义明确，但由于关系到地壳的质量和密度，因此暂时还不能准确求出。

1.1.3 正常高系统

正常高高程系统是以地面水平面作为参考平面的高程体系，用h表示。我国建立了以正常高为统一计算标准的高程体系，1956年黄海高程体系及 1985年国家高程标准是我国水利工程建设中常用的常规高程系统。

1.2 高程系统转换关系

由于椭球面与地球水准面不一致， 地球某点P沿铅垂线投射到似大地水准面的点为P0，P0在法线上投射在椭球面上的点为Q0，PP0的距离是Hg，P0Q0的距离是N（地球水准面间距），则H=Hg+N。地球上的球形面和地面水平面的高度差为高程异常，用ζ表示，则H=h+ζ。实际应用中，由于地球似大地水准面的精细程度分布不均，且具有一定的几何相关性，所以高程拟合仍是一种较为普遍的方法，GPS 高程拟合是一种求解 GPS 高程问题的数学方法。大地高与正常高之间的几何关系如图1所示。

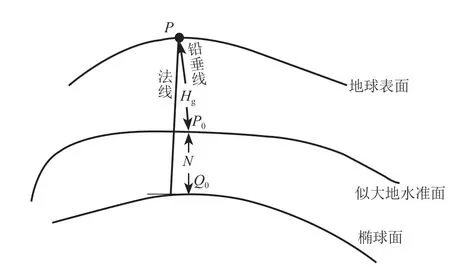
图1 大地高与正常高之间的几何关系

2 高程拟合方法

高程拟合方法主要有多项式和多面函数2类拟合方法，其中多项式拟合分为二次和三次多项式拟合。

2.1 二次多项式拟合法

根据 GPS 测得的大地高和水平测量结果的正常高计算高程异常ζ，公共点坐标可用二次多项式公式表示：

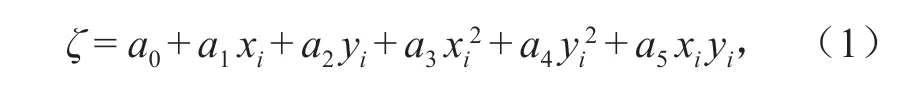
式中：x，y分别为 GPS 各公共点的平面坐标；a0，a1，…，a5为拟合待定参数，若测区内有n（n＞ 6）个控制点，且已知他们的高程异常为ξi（i= 1，2，…，n），则拟合系数a0，a1，a2，a3，a4，a5可由区域已知点上的高程异常通过最小二乘原理求定。

如果有m个共同点，设i= 1，2，…，m，则可以得到m个方程。利用m个未知数，通过m个方程求出唯一确定的系数，由此得出二次多项式。但在实际测量计算中，需要额外的观测数据求最或然值。用最小二乘法求多项式的系数，通常需要m＞ 6，离差公式如下：

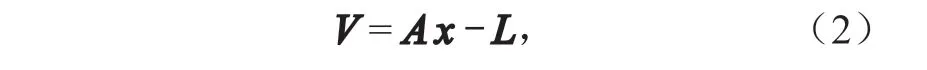
式中：V常称为离差；L为拟合值，L= [ζ1，ζ2，…，ζn]T；x= [a0，a1，a2，a3，a4，a5]T；A为离差的系数矩阵A，可表示为

假设参与拟合的点数为n，由式（1）可列出以下误差方程：

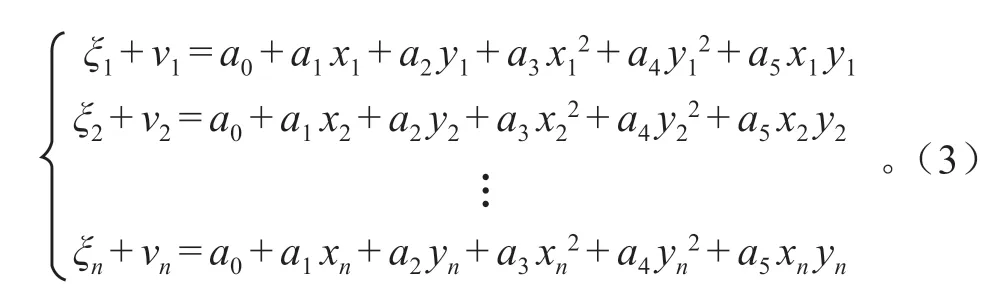
由此可知，V= [v1，v2，…，vn]T，vn为第n个拟合点的离差，由式（3）得出矩阵A。

2.2 三次多项式拟合法

三次多项式公式为

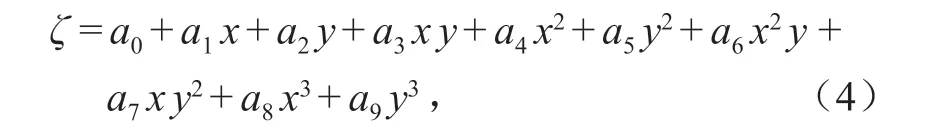
通过平差原理，列出的离差方程式如下：

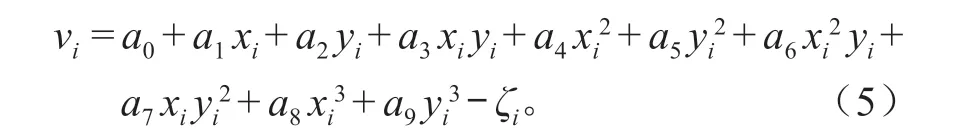
设i= 1，2，…，n，在存在n个拟合的情况下，各个矩阵表示为

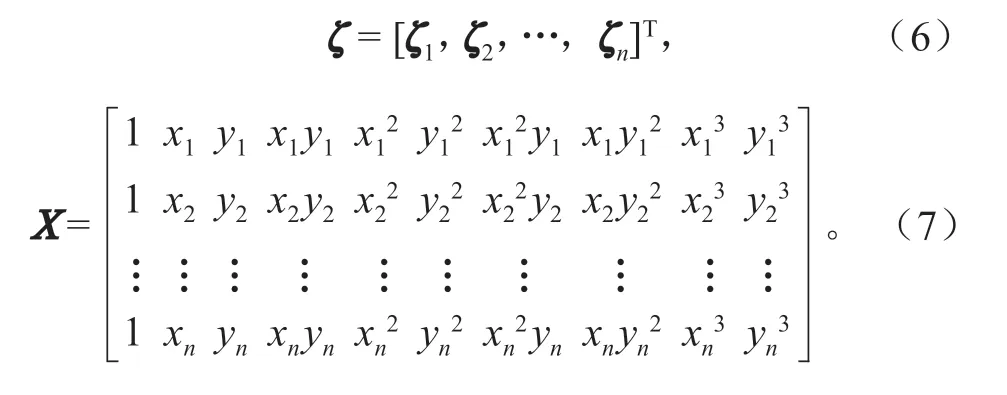
根据最小二乘原理，最终得到：

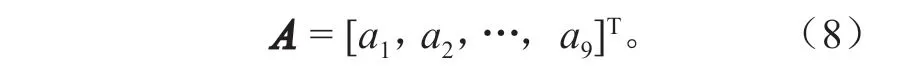
2.3 多面函数拟合

多面函数拟合法广泛应用在水准面差异、大地测量、重力异常拟合、垂直曲线偏移、地壳纵向变化等方面。基本思路为：如果任何一个规则的、不规则的、连续的曲面都可用若干单一的平面（单数值的数学平面）进行叠加，则在任何一个点处的高程异常值都可描述为

式中：αj为待定系数；ζ（x，y）为坐标（x，y）所对应的高程异常值；Q（x，y，xj，yj）为用来进行插值运算的一个简单的数学平面，也称为多个平面的核函数；n为一个简单的数学平面上的重叠平面的层数，数值等于一个区块扩展区域中的参与点数目。通常，核函数Q（x，y，xj，yj）是一种正的双曲线函数，即：

式中：j= 1，2，…，n，表示选定的结点编号，整体上有n个结点；δ为圆滑因子，也称光滑因子，用来对核函数进行调整，通常δ取一小正数或零。

对于正双曲面核函数，拟合精度随着光滑因子的增大而提高；对于倒双曲面核函数，光滑因子存在极大值，超过这个值，拟合精度就会降低。对于相同的光滑因子，正双曲面的拟合结果优于倒双曲面。

如果有m个符合点，则高程异常值计算公式为

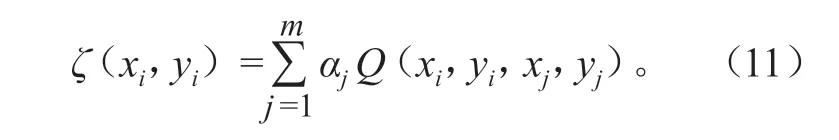
将式（11）用矩阵形式表示，即：

式中：α为对应不同结点的αj形成的矩阵；MQ为Qi j构成的矩阵，…，m；j= 1，2，…，n），则

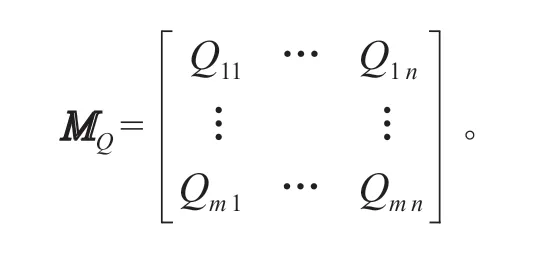
在m=n的情况下，方程（12）的解是唯一的；

当m＞n时，可得离差方程：

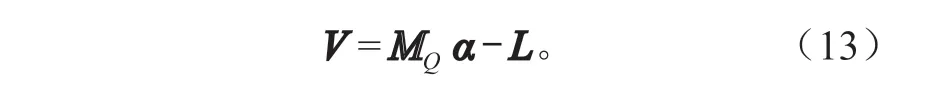
根据最小二乘原理，可得到待估参数α的最小二乘解从而得到权阵P。

3 高程拟合应用实例

在水利工程测量中，利用常规的高程测量方法在特殊环境地区进行测量，高程是很难测量出来的。而我国水利工程建筑物所处的环境比较特性，大部分水利工程的建设地点都位于山高谷狭、植被茂密、交通不便、国家水准标点稀缺的地方，所以在水利水电规划、大型水利设施建设中，第一层平面控制网通常使用 GPS 进行测量。而 GPS 高程拟合在水利工程中的应用适用于高山区，效果较好。为了将 GPS 高程拟合应用于实际 GPS 高程测量中，需要分析拟合的准确性，并进行适当的测试和设计。

某特大型水电站水库 Ⅲ 级 GPS 测控网络在一条河流上，由于地势的特殊性，这里山高谷狭，最大高度差为2500m。在整个测区内均匀布设12个水平面，对这12个水平面进行 GPS 观测，可以获得 WGS-84 坐标系内12个控制点的高程，先将D01，D03，D05，D07，D09，D11，D12 等作为已知资料，再将 D02，D04，D06，D08，D10 等高程异常点进行拟合。通过 3种高程拟合方法，先将 GPS 测出的控制点的x，y坐标代入公式中计算，为减小计算误差，通过6个具有代表性的未知数值，列6个方程，求得待定系数的大小，再求得每个 GPS 控制点的拟合高程异常值，最后依次求出拟合差值。3种方法拟合的结果如表1所示。

表1 各拟合方法的对比

从表1 可以看出，相同的点采用不同的拟合方法得到的拟合差值有很大差别：通过二次多项式拟合的差值最大值为 3.20 cm，最小差值为 1.45 cm，平均差值为 2.54 cm；三次多项式拟合差值最大值为 1.29 cm，最小差值为 0.01 cm，平均差值为 0.22 cm；多面函数拟合差值最大值为 1.89 cm，最小差值为 0.17 cm，平均差值为 0.51 cm。

为减小偶然误差，对某水利工程 Ⅳ 级 GPS 控制网联测了12个水准高程点，最大高差为2100m。该工程处于相对平坦的丘陵地带，海拔高度位于 25～55 m 之间，总项目中包括5条分散的干渠和3个村镇。拟合所选的公共点点号为 01～12，12 个点分布均匀，可覆盖整个测区，与上述实例计算过程一致。3种拟合方法的结果对比如表2所示。

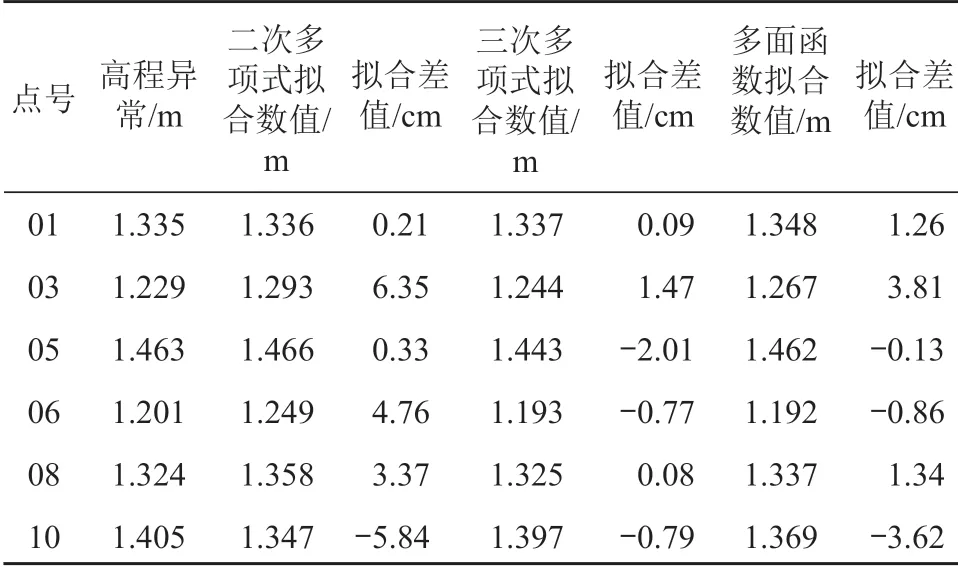
表2 各拟合方法的对比

从表2 可以看出：通过二次多项式拟合的差值最大值为 6.35 cm，最小差值为 0.21 cm，平均差值为 1.53 cm；三次多项式拟合差值最大值为 2.01 cm，最小差值为 0.09 cm，平均差值为 0.32 cm；多面函数拟合差值最大值为 3.62 cm，最小差值为 0.13 cm，平均差值为 0.30 cm。

综合2个实例，对 3种拟合方法拟合结果进行比较，表明三次多项式法比二次多项式、多面函数法的拟合效果更佳。三次曲面拟合，相比二次曲面拟合具有更高的拟合精度和较少的水利测量工作。对于陆地距离较远，以及跨河、海岛等情况，GPS 拟合高程能较好地解决拟合差值问题。GPS 拟合高程技术能有效减少水准测量时间，保证控制精度，大大提高工作效率。

4 结语

GPS 高程向正常高转换的精度与水准连测点的位置分布和点的个数有重要关系，这也影响转换精度。采用同一种拟合方法，不同点位的拟合精度也是有差异的，所以测量时，应尽量使测点分布在测区周围，并包含整个测区。

通过对 3种拟合方法的拟合差值的最大、最小及平均值进行比较得出：与二次多项式、多面函数的拟合方法相比较，三次多项式拟合方法更适用于水利工程测绘中，这与文献4和5等研究结果一致。

需要注意的是，由于转换方法的精度有限，GPS 在水利建设中的应用还存在一定的不足之处。GPS 监测水平位移的精度较高，而监测垂直位移的精度相对较低，比水平位移的监测精度约低 40%，在平原地区小范围内，GPS 高程的精度只能达到等外水准的要求。这种状况使得在水利工程勘测阶段、高精度变形监测中，还难以利用 GPS 同时精确测定水平和垂直位移。利用 GPS 建立各类控制网时，高程控制仍应用常规的几何水准测量方法测定，也可以采用 GPS 水准、曲面拟合的方法（如修正的 BP 网络拟合）提高 GPS 高程测量的精度。如果变形监测不考虑高程系统的差别而只考虑相邻2次的高差变化，则直接使用大地高差，精度会有进一步改善。虽然在水利测量中进行常规测绘，能够达到一定的应用需求，但在一些高精度的水利测量中，并不能完全满足精度要求。因此，研究更精确的转换模型，为更多水利测绘用户提供方便，是未来研究的一个重要课题。