级数收敛性的可视化

雍龙泉

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

级数在近似计算、电工学、信号处理、经济学等领域具有重要的应用，级数也可以看成是泰勒展开式的逆向应用[1]。判别级数是否收敛的方法较多：针对正项级数，有比较判别法、柯西判别法等；针对交错级数，主要采用莱布尼茨判别法[2-3]。从理论上证明级数收敛性的文献较多[4-6]，本文不从理论研究级数的收敛性，而是借助数学软件绘制级数前n项和的曲线，从直观上观察级数的收敛性。

1 正项级数

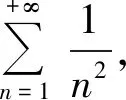
表1 例1对应的MATLAB数值计算、符号求和命令的代码

图1 例1级数的收敛过程

表2 例2对应的MATLAB数值计算、符号求和命令的代码

图2 例2级数的收敛过程

表3 例3对应的MATLAB数值计算、符号求和命令的代码

表4 例3级数的部分和、真实值e及绝对误差

图3 例3级数的收敛过程 图4 绝对误差图

图5 例4级数的前200项和 图6 例4级数的前2000项和

图7 例4级数的前10 000项和 图8 例4级数的前100 000项和

2 交错级数

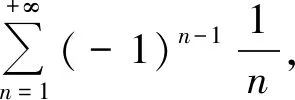
表5 例5对应的MATLAB数值计算、符号求和命令的代码

表6 例6对应的MATLAB数值计算、符号求和命令的代码

图10 例6级数的收敛过程

表7 例7对应的MATLAB数值计算、符号求和命令的代码

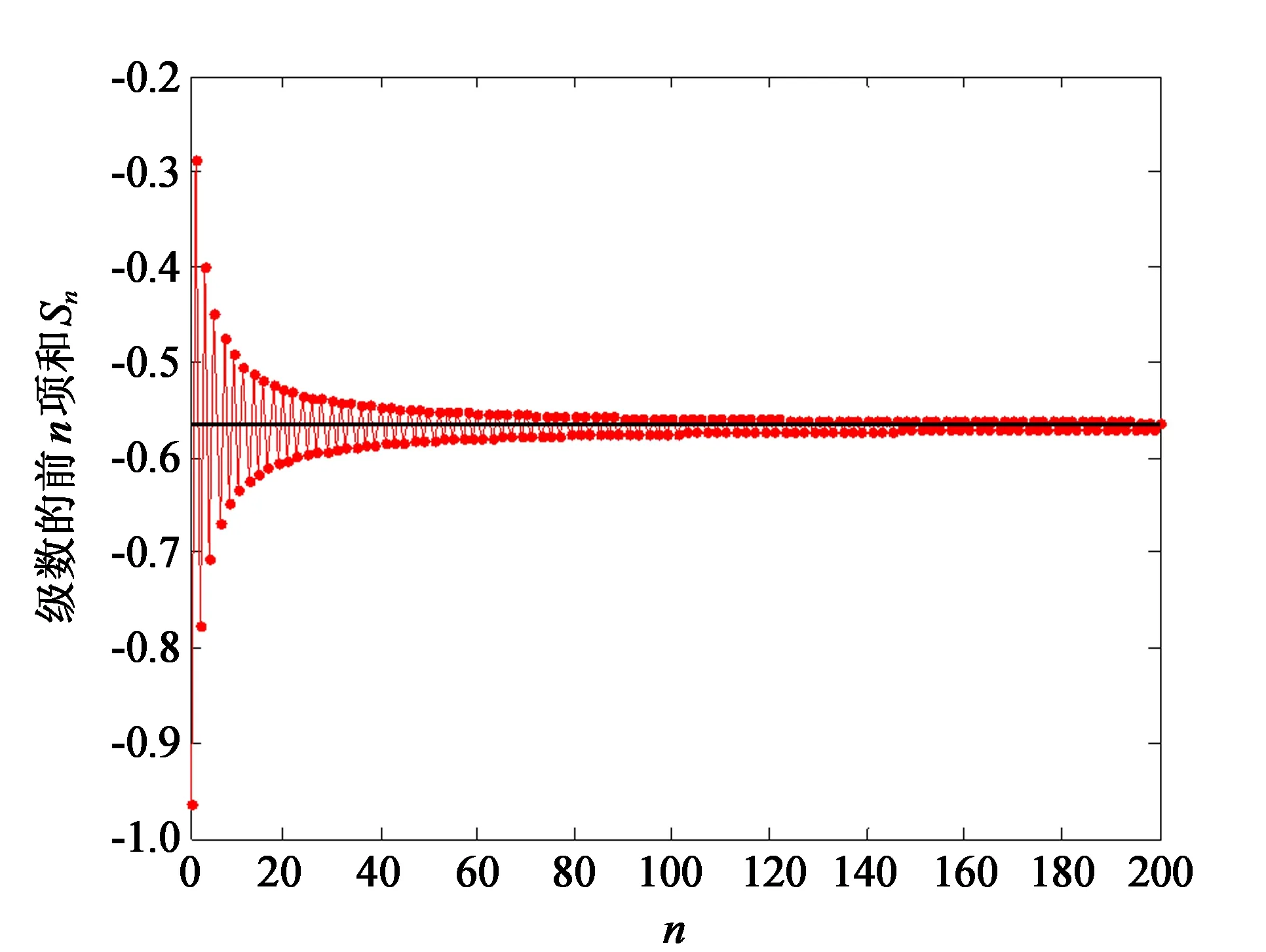
图11 例7级数的收敛过程

3 结语

上面几个例子从可视化角度展示了级数收敛或发散的过程。需要强调的是，MATLAB符号求和运算函数symsum尽管调用方便[7]，但是运算非常耗时(同等条件下耗时是数值计算的50～100倍)，若采用MATLAB数值计算，则耗时不到1 s。因此应尽可能少用MATLAB系统自带的符号运算函数，以便提高计算效率。