基于小波分析的德州市降水分析与预测
2022-10-27潘立云王玉珏
潘立云,王玉珏
(德州市水文中心,山东 德州 253016)
随着经济快速发展,国内极端气候也频繁发生,主要表现为局部地区气温上升、降水量增加,高海拔地区冰川融化加速,导致河流径流增加以及湖泊水位上升面积扩大等[1-3]。这些大规模气候变化引起了中国气候研究界的广泛关注[4-6]。一个世纪以来的这些温度和湿度变化是否是全球气候变暖的结果已经成为一个重要的研究课题。
气候因子作为典型的区域变量,被用来揭示行星风带和气压带的大尺度空间分带分布[7]。具有这些因素的研究通常存在重大的空间不确定性,它们受到自然条件和较小尺度的人类活动的影响,例如地形和地貌。在国内和国外进行的许多案例研究表明,区域气候是一个巨大而复杂的系统,很难准确预测极端气候的发生。因此,为了揭示区域气候过程的复杂性,必须考虑多个时空尺度,并且必须研究不同的方法。本文以德州市5 个雨量站1961—2016 年的时间序列数据为基础,以年均降水量为研究指标,通过小波分析来说明降水量在不同时间尺度上的变化趋势。然后,运用Mann-Kendal(l以下简称M-K)检验法,来检验这种趋势的显著性。
1 材料和方法
1.1 研究区域和数据来源
德州市位于山东省境内,属大陆性季风气候区,地处半湿润半干旱地区,年平均降雨量为571.3 mm。降水年际变化甚大,1964年降水量最多为1 049.8 mm,1968 年降水量最少为302.4 mm。因此,本文以德州市为研究对象对其气候变化以及多年降水变化进行分析。为全面分析德州市气候变化及降水变化,选择德州市5个雨量站逐月降水资料,详见表1。数据来自中国气象数据网,因此可以确保数据的准确性和精确性。

表1 选用雨量站相关信息
1.2 研究方法
1.2.1 小波分析
小波分析是一种分析信号时间尺度的多分辨率分析方法,可以有效分析径流和气候变化过程的周期性。本文的主要研究内容是基于小波分析研究不同时间尺度上的非线性趋势。
小波分解和重构的原理如下。考虑时间序列X(t),如温度、降水量、湿度等,可建立父小波和母小波的投影序列,有k{k=1,2,…,N}和s{s=2j,j=1,2,…,J},N为自然数。
展开式中的系数由下式给出:
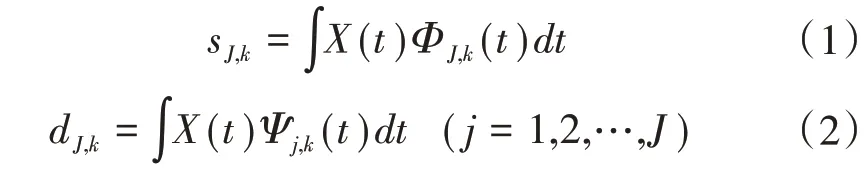
式中:J为数据点数量可持续的最大尺度;ΦJ,k=2-j/2Φ[(t-2jk)/2j] 为父小波;Ψj,k=2-j/2Ψ[(t-2jk)/2j]为母小波。通常,父小波用于最低频率的平滑分量,这需要具有最广泛支持的小波;母小波用于较高频率的细节分量。
信号X(t)的表示可以由以下公式给出:
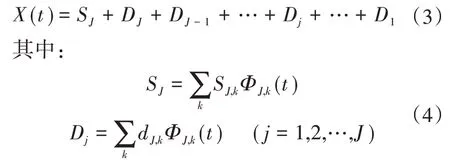
通常情况下,则:
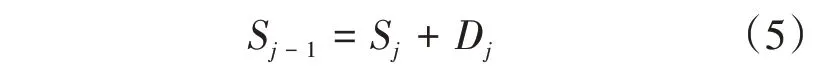
其中,{SJ,SJ-1,…,S1} 是函数X(t)在不断增加的细化水平上的多分辨率近似序列。
使用Symmlet 作为基小波,对多个尺度函数进行了试验,以确定最适合该数据集的小波。结果发现,“Sym8”产生了最稳健的定性结果。因此,本文使用“Sym8”来近似模拟气候演变过程的趋势。
1.2.2 回归分析
尽管区域气候是一个庞大而复杂的系统,仍然可以建立湿度、温度和降水量的统计关系。为了简化计算,本文还根据各时间尺度的小波分析结果,进行了回归分析,以检验降水的影响趋势。
1.2.3 M-K检验
M-K检验法是一种非参数统计检验方法,通常用于检验时间序列数据中时间趋势的显著性。M-K检验法的特点是不需要预先假设数据样本的统计分布。
M-K统计检验的统计值Zc表示为:

式中:xk和xi为顺序数据值;n为数据的长度。测量趋势的指标即倾斜度表示如下:

式中:β表示上升趋势;-β表示下降趋势。
M-K 检验法可按以下方式使用:对于H0=0、β=0的假设,若 |Zc|>Z(1-α)/2则拒绝零假设;其中,Z(1-α)/2为标准正态方差,α为检验的显著性水平。
2 结果与讨论
2.1 年降水量变化特征
由图1 可以看出,研究区1961—2016 年降水整体分为3 个明显的下降阶段,分别为1961—1968、1976—1990 和1994—2008 年;同时,有3 个明显的上升阶段,分别为1969—1975、1991—1993 和2009—2012年,在2012年以后降水波动幅度较大。研究区范围内降水最大超过1 000 mm,最低接近200 mm。
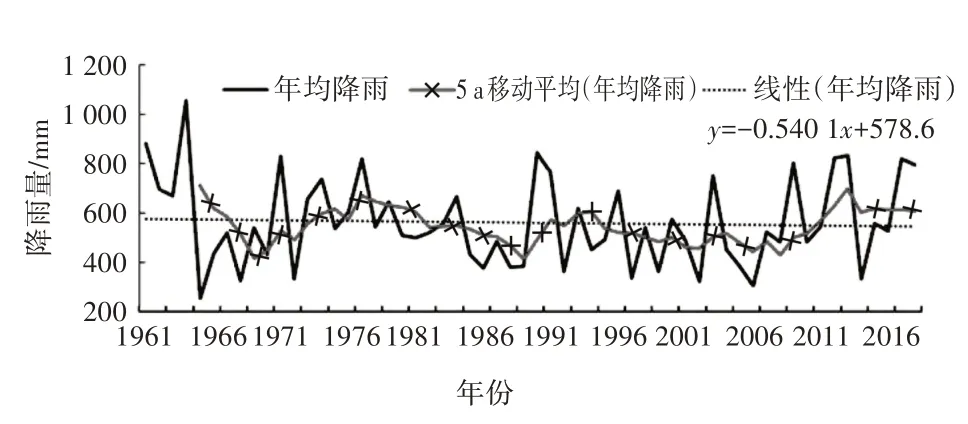
图1 德州市年均降水变化规律
2.2 降水时空分布特征
研究区年均降水系列小波系数实部等高线,如图2所示。
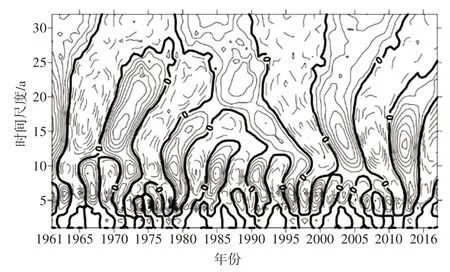
图2 小波系数等值线
图2 能反映研究区的降水年周期和强度,实部小波系数为正,表示雨季,用实线表示;为负,表示旱季,用虚线表示;为0,表示降水均衡,用粗线表示。由图2 可以看出,研究区降水量在15 a 尺度上最为明显,有12 个旱涝交替周期。1961—1963、1969—1974、1979—1984、1989—1995、2001—2006 和2011—2016 年间降水较大;1963—1969、1974—1979、1984—1989、1995—2001、2006—2011 年间降水较小。降水过程有一定的波动,但总体上1961—2016年的年径流以15 a周期为主。
以上分析表明,研究区降水具有约15 a 的周期性变化,可以反映研究区降水变化特征及其演变趋势。
为了确定每个站的主要周期即降水序列的主要功能,计算研究区的方差,结果如图3所示。
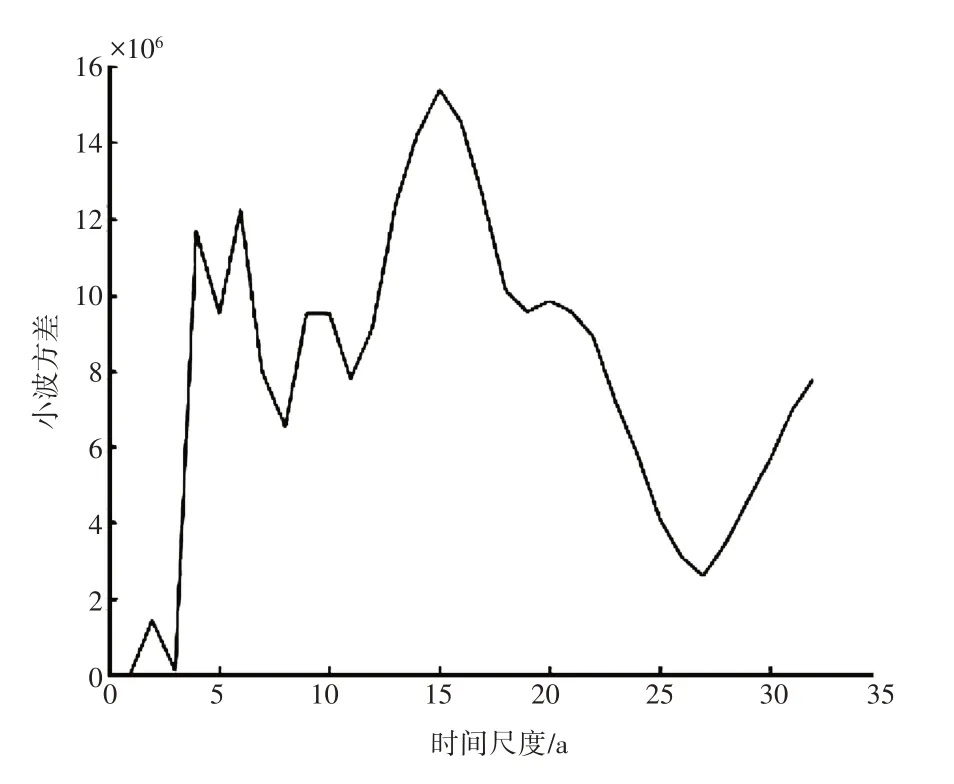
图3 小波方差
由图3 可以看出,研究区降水具有多个时间尺度特征,共有5 个峰值,对应15、6、4、10 和20 a 振荡周期,其中15 a时间尺度小波方差最为明显,表明第一主周期为15 a,2~5 个周期存在一定差异,对应Morlet 小波系数真实等值线图,确定了研究区年均降水在整个时域内的变化特征。
2.3 年均降水M-K检验结果
采用M-K 方法对研究区域5 个雨量站1961—2016 年的年平均降水变化的显著性进行了检验。结果表明,整个流域的年平均降水显著下降,在0.05置信水平下,年平均降水变化为0.540 1 mm。研究区域大部分地区的年增长幅度为负。临邑的年降低幅度最大,其次是德州、陵县和宁津,武城的变化幅度较为温和。
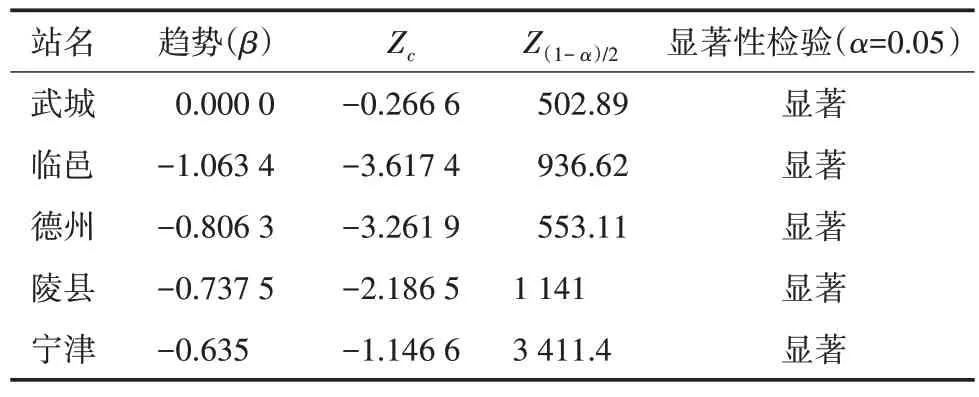
表2 年均降水趋势的M-K检验
3 结语
小波分析和M-K检验的分析结果为研究区1961—2016 年的区域气候变化提供了一些依据。由上述分析结果可知,1961—2016 年研究区降水的年际变化以多雨—少雨—多雨—少雨—多雨交替为主,总体呈下降趋势;1961—2016 年期间,研究区的气候变化过程作为年平均降水量的时间序列数据,呈现出非线性趋势;在小波分析中,使用不同的时间尺度会导致不同的趋势变化,其中15 a周期最为明显;在0.05 置信水平下,M-K 非参数检验的结果表明,1961—2016 年期间年平均降水的上升趋势显著,也就是说,由年平均降水上升所暗示的变暖趋势是显著的。降水周期的预测是未来研究的一个重要方向,通过对某一局部区域未来降水预测,可以减少降雨事件的不确定性,降低降雨对研究区的不利影响。
