“井工厂”不同压裂模式下裂缝扩展规律数值模拟研究

张皓宇，陈军斌，王涛，赵峥延，寇园园

(1.西安石油大学 石油工程学院，陕西 西安，710065；2.陕西省油气井及储层渗流与岩石力学重点实验室，西安石油大学，陕西 西安，710065；3.中国石油长庆油田分公司 第三采油厂，宁夏 银川，750005；4.中国石油长庆油田分公司 油气工艺研究院，陕西 西安，710065)

水平井体积压裂技术已被证实为页岩储层经济开采的关键技术，通过尽可能沟通天然裂缝而形成复杂程度高的裂缝网络[1]。同时，为了提高改造效率和降低作业成本，开发页岩油气通常采取“井工厂”模式[2]。为加强缝间应力干扰，提高裂缝复杂程度，将单口井的压裂次序由顺序压裂改变成跳跃式压裂[3-4]。随着“井工厂”模式的推广，出现了多口井交替压裂的同步压裂技术，在此基础上优化压裂次序和布井方式，发展出常规拉链式、改进拉链式压裂技术，进一步促进形成复杂缝网[5-6]。无论哪种压裂技术，多条裂缝扩展都会受到周围裂缝施加的应力干扰，导致井筒周围原始地应力场发生改变，从而导致裂缝扩展过程中形态不一致[7]。国内外学者针对水平井多裂缝起裂、扩展及应力干扰问题采用多种不同的方法进行了研究[8]。于永军等[9]引入3 类断裂力学干扰因子，求解了有限尺度地层内部裂缝尖端应力强度因子，分析了裂缝干扰与竞争起裂行为。冯其红等[10]采用扩展有限元方法分析了改进拉链式压裂过程中簇间距、地应力等因素对各条裂缝扩展形态和缝间诱导应力场的影响。刘乃震等[11]基于真三轴水力压裂模拟系统，开展压裂缝内流体压力、段间距等因素对致密砂岩储集层多裂缝扩展形态影响的实验。程万等[12]采用边界元法研究岩体在压裂液作用下的变形程度，建立了流-固耦合的水平井多条水力裂缝同步扩展模型。目前，人们对应力干扰的研究大多集中在单井，而且主要研究多簇同时起裂的相互影响，而对“井工厂”模式下的多井逐次顺序压裂、常规拉链式压裂和改进拉链式压裂工艺下诱导应力场分布特点以及射孔段间距、井间距对各工艺下诱导应力场的影响特征缺少深入研究，并且未结合压裂工艺研究诱导应力场对裂缝形态的影响。为了深入分析“井工厂”压裂模式下应力场对多裂缝扩展的干扰规律，本文作者基于多孔介质流-固耦合理论，建立水平井分段分时扩展力学模型，利用应力计算模型建立叠加应力场，在ABAQUS 商业有限元分析软件基础上进行二次开发，应用扩展有限元方法深入研究逐次顺序压裂、常规拉链式压裂和改进拉链式压裂工艺下调整射孔段间距、井间距对诱导应力场分布的影响，以及在应力干扰下人工裂缝长度、宽度和偏转角度变化规律，以便为“井工厂”模式下复杂缝网结构预测和压裂工艺优化提供依据。

1 水力压裂扩展有限元模型

1.1 多孔介质流-固耦合模型

水力压裂时岩石骨架受到缝内流体压力和孔隙压力等外力作用，假设裂缝扩展过程受力平衡，则系统平衡的强形式为[13]

在解域Ω内，边界条件为

式中：b为体积力向量；Ω为不包含裂缝的积分空间；为外载荷；Γt和Γu分别为外力边界和位移约束边界；σ为应力张量；为外边界上规定的位移；Γc为裂缝内边界；n+和n-分别为Γ+c和Γ-c的外法线；p为作用在裂缝面Γc上的流体压力。

定义基于Biot系数的多孔介质有效应力[14]为：

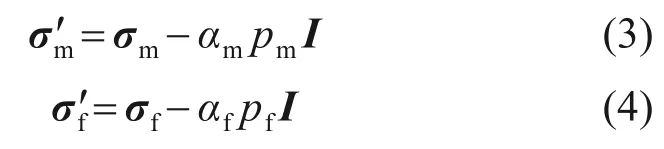
式中：σ'm为基质有效应力，MPa；σ'f为裂缝有效应力，MPa；σm为岩石基质总应力，MPa；σf为裂缝壁面总应力，MPa；αm为多孔介质中基质的Biot系数；αf为裂缝面的Biot 系数；pm为基质孔隙压力，MPa；pf为裂缝壁面孔隙压力，MPa；I为单位矩阵。

基于虚功原理，上式等效积分弱形式为：

式中：δε为虚应变率；δu为虚位移；“:”为张量的双点乘；p+作用在Γ+上，p-作用在Γ-上。

以润湿液体孔隙压力为节点变量，在单元上进行插值，可得多孔介质的连续性流动方程等效弱形式[15]：

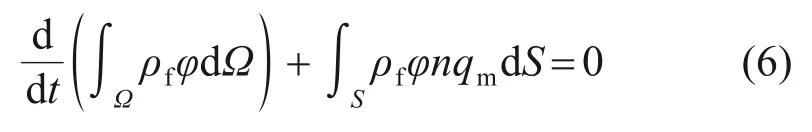
式中：ρf为液体密度，kg/m3；φ为地层孔隙度；qm为液体在基质中的平均流量，m3/s；n为曲面S的外法线方向；dS为计算微元的体积。

ABAQUS 通过设定边界条件，采用直接法求解应力平衡方程和流体连续性方程的耦合方程矩阵，可得到模拟区域的应力、应变、位移等相关参数的分布特征。

1.2 扩展有限元方法

扩展有限元单元节点类型示意图见图1[16]。由图1可知：扩展有限元的单元类型包括裂缝贯穿单元、缝尖单元、过渡单元和普通单元，其中，前3种单元均与裂缝相关[16]，对应的节点类型分别为贯穿加强节点、缝尖加强节点和过渡节点。

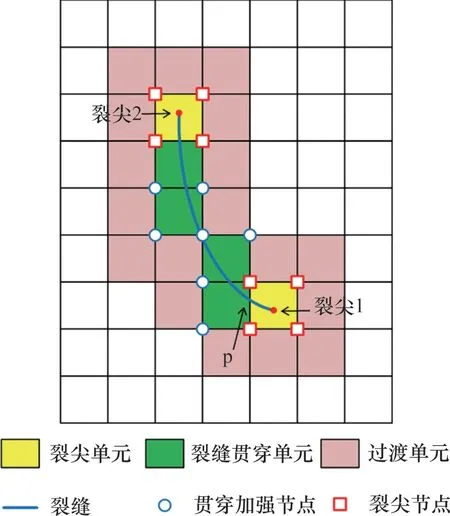
图1 扩展有限元单元节点类型示意图[16]Fig.1 Element and node representation in XFEM[16]

扩展有限元模型内的裂缝，其不连续性可以表示为标准有限元位移uFE(x)和增强位移uenr(x)之和。对于裂缝问题，增强位移包括裂纹面两端增强节点位移和裂纹尖端增强节点位移，公式如下[17]：

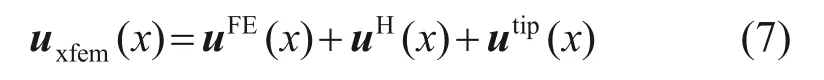
式中：uFE(x)为标准有限元位移自由度向量；uH(x)为裂纹面两边加强节点位移自由度向量；utip(x)为裂纹尖端加强节点位移自由度向量。

由于Heaviside 阶跃函数(H(x))只能描述到p点为止的不连续位移场，引入Belytschko 和Black提出的渐进裂纹尖端函数(Fl(x))描述尖端处的奇异性，式(7)可改写为[17]

其中：I为常规有限元节点数；J为裂纹面两侧增强节点数；K1和K2为裂尖增强节点数；Ni(x)为所有普通节点的标准有限元形函数；ui为普通节点的位移；Nj(x)为裂缝贯穿单元的形函数；aj为裂缝贯穿单元节点的位移；Nk(x)为裂缝尖端单元的形函数；bl1k和bl2k为裂缝尖端两点的位移；Fl(x)为裂尖增强函数在高斯点x处的值。

对于脆性材料中的张开裂纹，裂纹尖端的应力和应变场具有奇异性，近尖端的4个富集函数用Williams提出的渐进解，在局部裂纹尖端极坐标系下的定义为[18]

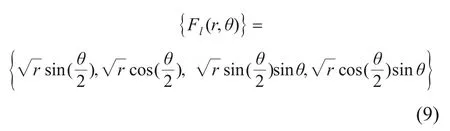
式(9)中，(r，θ)为高斯点x在局部裂纹尖端极坐标下的坐标，不连续，其余3项连续。需要指出的是，函数Fl(x)仅适用于直线裂缝，对于带折点的裂纹，裂纹面两侧Heaviside增强和裂尖增强可能不一致而导致计算出错。BELYTSCHKO 提出映射法解决这一问题[19]。

H(x)在裂缝尖端的极坐标系下是非连续的，其表达式[20](在裂纹上方H(x)取1，裂纹下方取-1)如下：

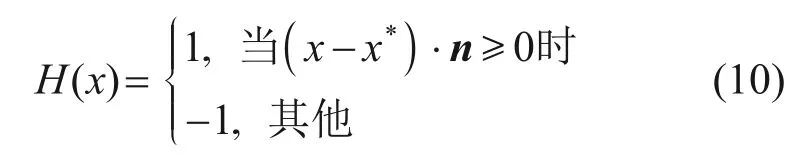
其中：x为1 个高斯点；x*为最靠近x的裂纹上的点；n为x*处垂直于裂纹的单位向量。

破裂准则采用最大主应力准则[21]：

式中：为最大临界主应力； 为Macaulay 括号，用来指定纯压应力率不能引起损伤，只有当最大应力达到某一临界值时，损伤开始。

引入损伤标量D来判定损伤演化[21]：

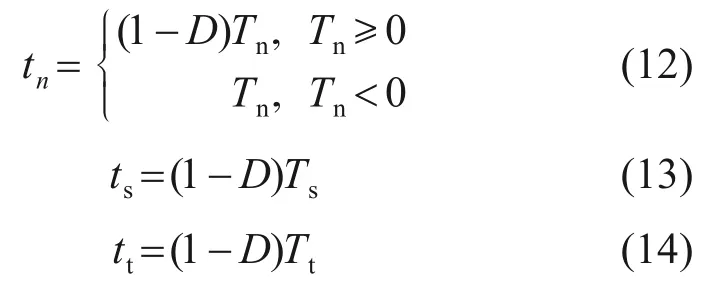
其中：tn，ts和tt分别为应力矢量t的法向应力分量和第一、第二切向应力分量；Tn为线弹性条件下受力单元法向应力分量；Ts和Tt分别为受力单元第一和第二切向应力分量。

2 水力压裂裂缝应力干扰模型

2.1 单条水力裂缝诱导应力计算模型

以平面应变模型为基础，建立垂直裂缝诱导应力场几何模型。假设地层各向同性，裂缝为张开型，不考虑剪切滑移，缝高固定，缝内流体为层流且不考虑温度和滤失的影响。取拉正压负，当裂缝内有一定净压力时，该净压力在平面内产生诱导应力公式[22]如下：

式中：σx，σy和σz分别为x，y和z方向诱导力分量，MPa；pnet为裂缝内净压力，MPa；υ为地层泊松比；c为裂缝半长，m；r，r1和r2分别为参考点到裂缝中心、裂缝下缝高底部、裂缝上缝高顶部的距离，m；θ，θ1和θ2分别为r，r1和r2与z轴的夹角，(°)。

2.2 连续压裂诱导应力计算模型

按照应力叠加原理，先压的n条裂缝在点(x，z)处产生的诱导应力的总和可以表示为[23]

其中：σax，σay和σaz分别为最小主应力、最大主应力和垂向应力方向上的诱导应力，MPa；σxi和σzi分别为第i条裂缝对第n条裂缝在x和z方向产生的附加应力，MPa。

在原始地层条件下，地应力场由最大主应力σH、最小主应力σh和垂向应力σv组成。设σ'h为增加诱导应力后的最小主应力，σ'H为增加诱导应力后的最大主应力，σ'v为考虑诱导后的垂向应力。水力裂缝诱导应力场数学模型示意图见图2。由图2可知水压至裂后，井筒周围新的应力场由原始地应力场与诱导地应力场叠加而成：

图2 水力裂缝诱导应力场数学模型示意图Fig.2 Diagram of mathematical model of stress field induced by hydraulic fracture

参考SOLIMAN等[24]研究成果，在xOy平面定义裂缝转向发生的条件是叠加后应力场σ′H-σ′h≤0，代入式(16)和式(17)得到式(18)，发现当两向诱导应力差大于等于原始两向地应力差时，裂缝转向。

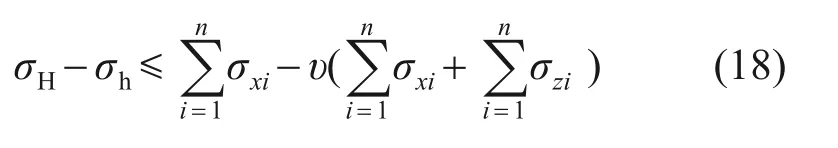
3 不同压裂模式数值模拟分析

3.1 数值模拟实验准备及结果验证

在ABAQUS 中进行扩展有限元数值模拟时，使用Geostatic 和Soil 模块，设定17 个分析步模拟真实地层条件下的流固耦合。其中，第1个分析步是施加初始地应力，其余16 个分析步则是按照“井工厂”模式不同压裂工艺的施工顺序进行模拟，每条裂缝施工步包括压裂注入和地层泄压2个阶段。同时，内置孔压单元模拟地层岩石孔隙及线弹性力学性质，岩石基质采用CPE4P 正四边形单元网格，人工裂缝采用T2D2 网格。图3所示为本文数值模型简图[20]。模型长×宽为150 m×150 m，网格边长为1 m。在模型x和y方向的边界上分别施加位移约束，同时，边界A′B′，B′C′，C′D′和D′A′孔隙压力均设置为20 MPa，水平井筒方向为最小水平主应力方向。其他数模参数如下：岩石弹性模量为15 GPa，泊松比为0.24，储层渗透系数为1×10-7m/s，孔隙度为10%，储层初始孔隙比为0.1，储层滤失系数为1×10-14m/(Pa·s)，孔隙压力为20 MPa，抗拉强度为2.2 MPa，压裂液排量为5×10-5m3/min，压裂液黏度为0.001 Pa·s，液体密度为9.8 kN/m3，最小水平主应力为8 MPa，最大水平主应力为10 MPa，射孔长度为1 m，射孔段间距为30 m，每条裂缝注入时间为100 s，地层泄压时间为3 600 s。

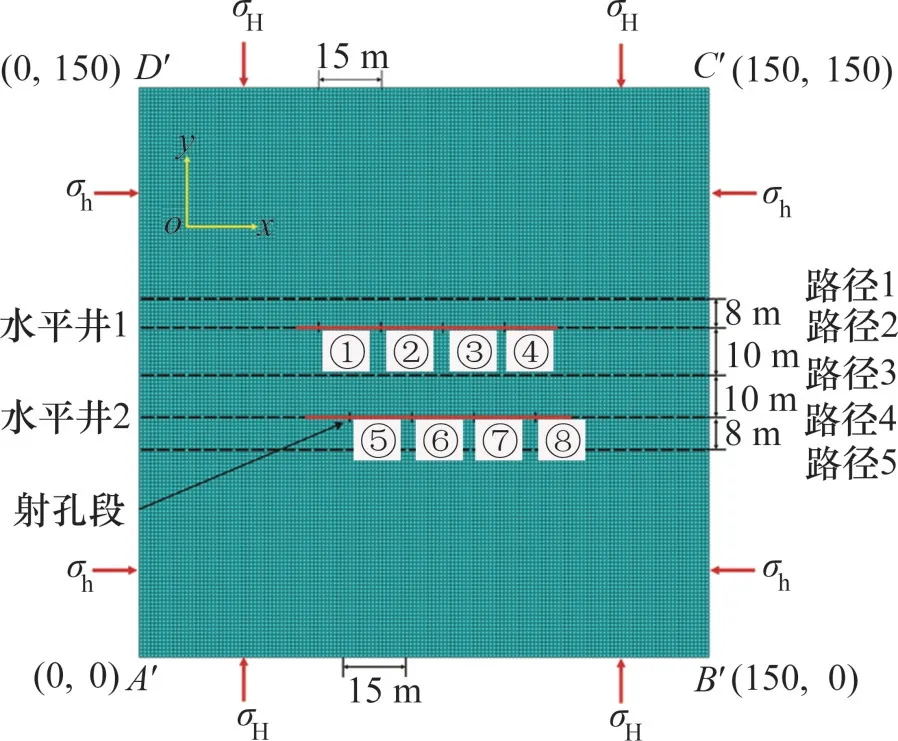
图3 数值模型简图[20]Fig.3 Schematic diagram of numerical model[20]

文献[11]指出，当水平应力差异系数为0.25时，应力反转程度较大。作为对照及验证，数模实验条件与文献[11]中条件保持一致。数模实验结果表明1 号裂缝、2 号裂缝和3 号裂缝均发生了转向，且裂缝扩展形态与文献[11]中的结果趋于一致，这说明本模型在模拟裂缝转向及其动态扩展规律具有一定的可靠性，能够应用于水平井分段分时压裂中的动态裂缝扩展研究。数值模拟结果与物理实验结果对比见图4。

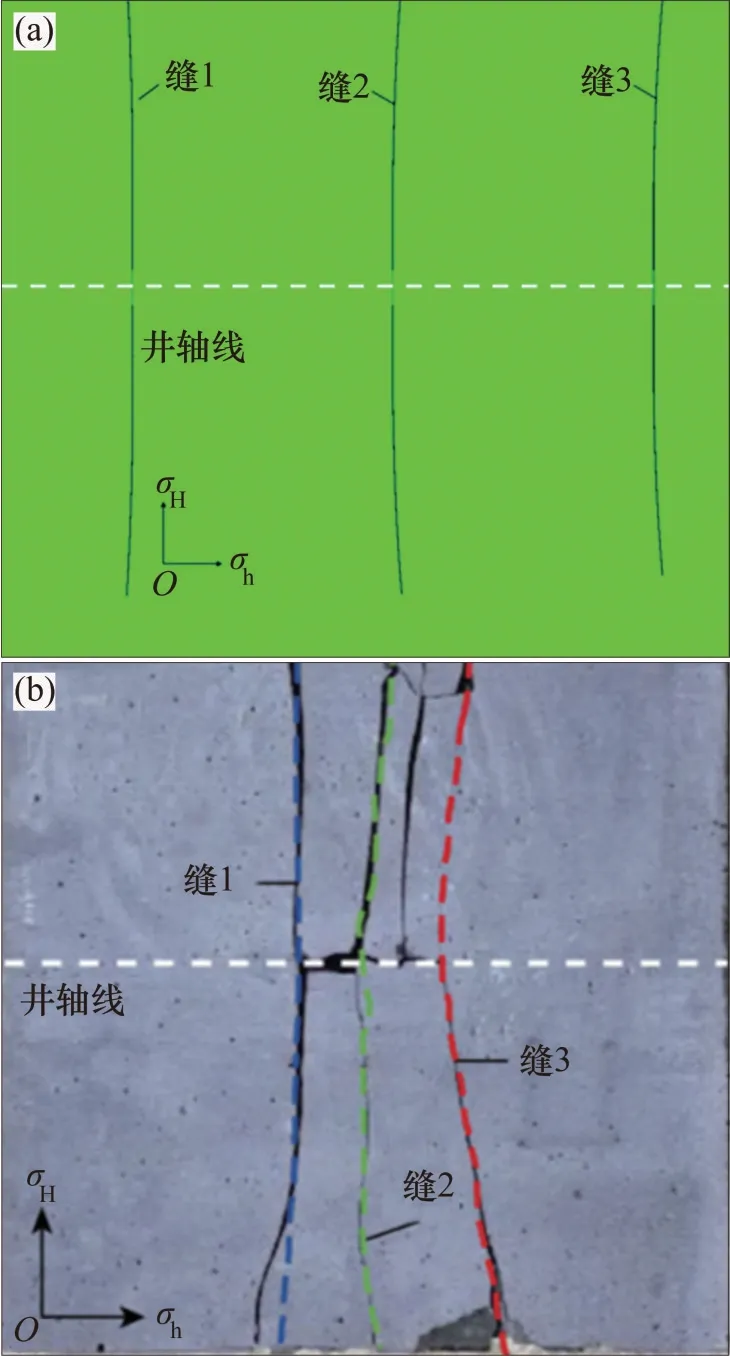
图4 数值模拟实验及验证结果Fig.4 Numerical simulation test and verification results

由于ABAQUS 采用虚拟节点来模拟裂纹随机扩展，裂缝在通过单元网格时，同一侧的节点符号相同，两侧节点符号互异，并且裂尖每次都会穿过整个单元格。根据这些特性，采用Python 编写动态提取裂缝几何参数的工具，具体二次开发流程如图5所示。

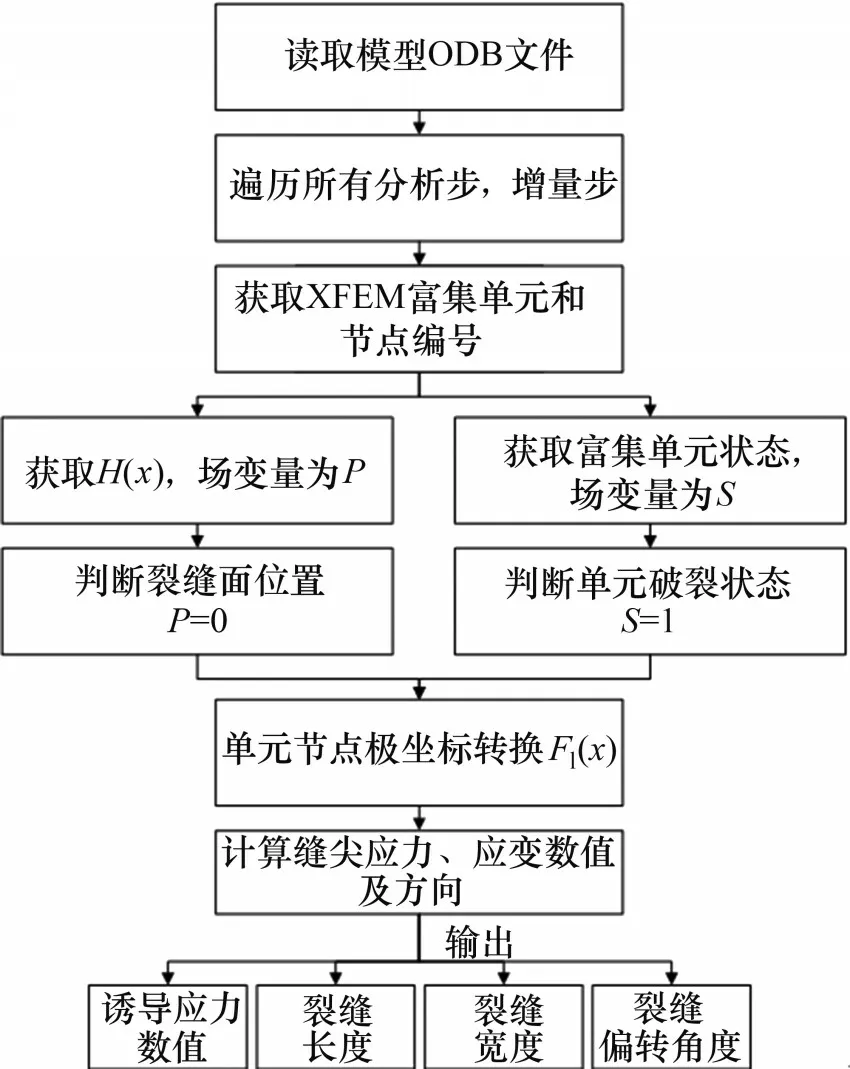
图5 ABAQUS二次开发流程Fig.5 Secondary development flows of ABAQUS

3.2 “井工厂”模式诱导应力场影响因素分析

为了研究“井工厂”模式下同井缝间和多井井间诱导应力场的分布情况，定义xOy平面射孔段间距依次为15，20 和25 m，2 口井之间间距依次为20，25和30 m。设定5条路径，其中，路径1和路径5 分别穿过水平井1、水平井2 的井轴侧翼缝长中部，路径2 和路径4 沿2 口井的井轴分布，路径3为2口井对称轴线，用以全方位观测缝间干扰和井间干扰现象。路径设定如图3所示。

3.2.1 “井工厂”模式不同路径诱导应力分布

初始数值模拟方案设置射孔段间距为15 m，2口井之间间距为20 m，图6所示为最大主应力云图。从图6可知：在常规拉链式压裂和改进拉链式压裂模式下，2口井的水力裂缝的叠加应力场明显强于逐次顺序压裂工艺的叠加应力场，应力干扰现象更突出。图7所示“井工厂”不同压裂模式下路径1、路径3路径5的诱导应力分布。由图7(a)可知：逐次顺序压裂时，水平井1各缝受到的诱导应力比水平井2 的大。这是因为裂缝在逐次开启时，先压缝中流体不断向地层滤失，导致缝内净压力下降，水平井2后续裂缝起裂也只受到同井的缝间干扰，叠加应力场较小。为了提高裂缝转向的效率，尽可能沟通远端天然裂缝形成缝网，在逐次顺序压裂工艺基础上发展了常规拉链式压裂工艺，即对2口相邻水平井间的相对裂缝进行交替压裂的一种工艺技术。由图7(b)可知：由于裂缝起裂次序发生变化，2口井缝间干扰和井间干扰程度均得到了较大加强。但在该工艺下，水平井2的缝间干扰和井间干扰出现交替“跳动”现象，存在一定的施工安全隐患。改进拉链式压裂工艺，即先压水平井1的1号和2号缝，再压水平井2的1号缝。由图7(c)可知：相较于前2种压裂方式，这种工艺在增大缝间干扰的同时，降低了2 口井的井间干扰，兼顾了页岩储层复杂缝网和施工安全的需要。

图6 数值模拟最大主应力云图Fig.6 Numerical simulation of the maximum principal stress

图7 不同路径诱导应力场分布特征Fig.7 Distribution characteristics of stress field induced by different paths

3.2.2 不同段间距下诱导应力场变化

从路径曲线可以看出，随着段间距增加，各工艺下水力裂缝受到的诱导应力均降低，但2口井的响应方式和敏感程度均不相同。在不同压裂模式且井间距分别为15，20和25 m时，不同路径应力场的变化如图8所示。由图8可知：对于水平井1，逐次顺序压裂和改进拉链式压裂下缝间诱导应力在降低的同时，由指端到根端依次增大，段间距的改变仍未影响这种对应关系；随着段间距进一步增大，诱导应力由拉应力转变为压应力，这说明近井筒周围产生诱导压应力，远离井筒两侧产生诱导拉应力，靠近缝尖处拉应力最大；增加段间距可使地层恢复原始的破裂压裂，降低水平井1 后续压裂施工的风险。对于水平井2，随着段间距增加，逐次顺序压裂下路径3诱导拉应力发生转变，使其受到水平井1裂缝诱导开启的可能性降低，施工压力将会升高。而改进拉链式压裂在增加段间距的同时，仍保留水平井1对水平井2的诱导作用，可有效降低后压井的施工压力。常规拉链式压裂对段间距最敏感，增大段间距后，缝间和井间干扰下降，减少诱导应力的“跳动”现象，2口井中各缝的诱导应力区域稳定。因此，在某些只能采用常规拉链式压裂工艺的情况下，可通过改变段间距降低施工风险。

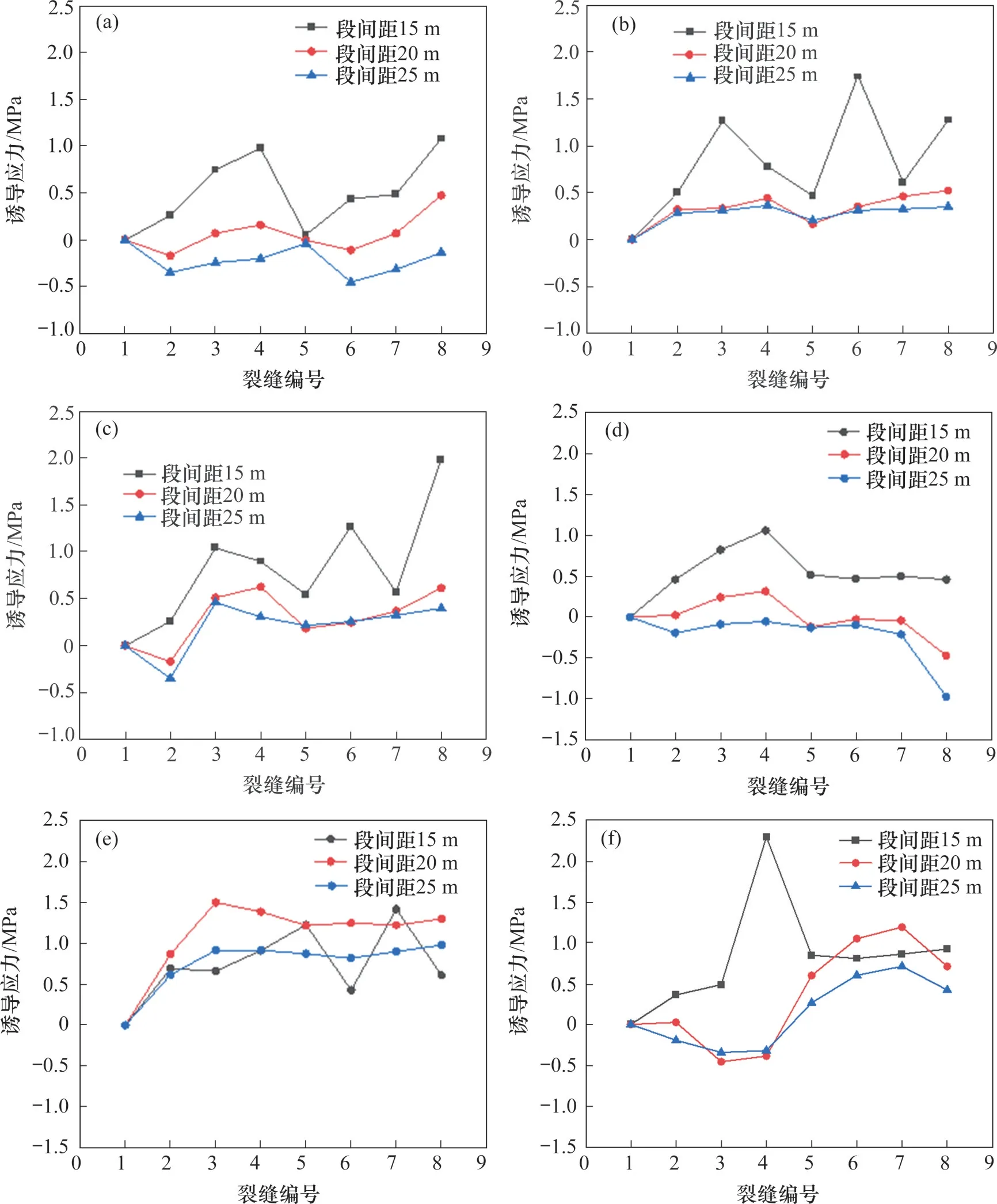
图8 不同压裂工艺下射孔段间距对诱导应力场的影响Fig.8 Effect of perforation interval spacing on induced stress field under different fracturing processes

3.2.3 不同井间距下诱导应力场变化

在不同压裂模式且井间距分别为20，25 和30 m 时，不同路径应力场的变化如图9所示。由图9可知：对于逐次顺序压裂，增加井间距并不会降低同井的缝间干扰，反而增大了水平井2 中间裂缝受到的集中应力干扰。这是因为随着井间距增大，2 口水平井的裂尖部分同时靠近井对称轴，由裂尖集中应力带来的扰动加剧。因此，在多井压裂时，应合理优化井间距，避免井间裂缝“头对头”的情况。在常规拉链式压裂模式下，增加井间距对2口井的影响不同。水平井1中部裂缝和水平井2 指端裂缝受到的缝间扰动作用明显减小，并且诱导应力的“跳动”现象减弱，对施工有利。水平井2 受到的井间诱导应力跳动规律发生反转，虽然诱导应力减小，仍保留有形成复杂缝网的能力。改进拉链式压裂对井间距的调整最敏感。增大井间距可有效降低水平井2 各裂缝受到的井间扰动，同时，诱导应力场的分布特征与逐次顺序压裂相似，且峰值比常规拉链式压裂的略高。因此，通过改进拉链式压裂工艺调整井间距可降低施工风险，同时保留有一定的体积改造能力。

3.3 诱导应力场对裂缝形态的影响分析

水平井多裂缝扩展形态是储层改造效果评价的关键。在“井工厂”压裂模式下，井间干扰的加入对人工裂缝的形态产生巨大影响，因此，有必要对诱导应力场下裂缝扩展形态特征进行定量研究，为现场布井射孔提供参考。

3.3.1 诱导应力对裂缝偏转的影响

由于xOz平面中诱导应力存在剪切应力分量τxy，最大、最小主应力的方向发生改变，后起裂的裂缝在先压裂缝的诱导应力影响下，与原来设计的方向产生偏差。转向角度计算公式[25]如下：

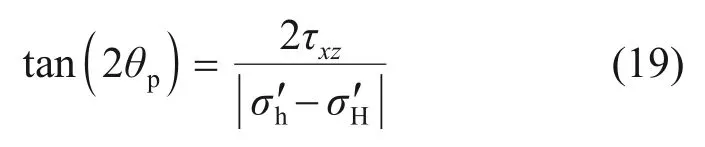
式中：θp为偏离原始最大主应力的角度。

“井工厂”压裂模式下裂缝扩展形态如图10(a)所示。从图10(a)可见：2口井中各缝均有不同程度偏转；在逐次顺序压裂模式下，8条裂缝偏转最大主应力的角度为0°～8°，常规拉链式压裂模式为0°～10°，改进拉链式压裂模式为0°～15°；水平井2的裂缝偏转程度比水平井1的大，这说明裂缝的偏转不仅来自同井的缝间干扰，而且会受到邻井的井间干扰，“井工厂”多井压裂的模式明显优于单井体积压裂的缝网改造方式。通过计算所有数值模拟方案的诱导应力并与裂缝偏转角度绘制关系曲线，见10(b)。从图10(b)可知：逐次顺序压裂拟合曲线为y=8.651x0.766(R2=0.91)，常规拉链式压裂拟合曲线为y=7.853x0.398(R2=0.72)，改进拉链式压裂拟合曲线为y=8.493x0.642(R2=0.89)，且文献[26]中的物理实验结果也与逐次顺序压裂拟合结果高度吻合，这说明提高诱导应力可显著增大裂缝偏转角度。这一研究结果对现场体积压裂具有很强的指导意义。现场施工时，裂缝扩展模式兼顾分簇同时起裂和分段分时起裂，前者由于压裂液同时进入各簇，缝内净压力较高，相邻两簇受到很大的诱导应力，裂缝偏转角度过大，导致部分簇不能完全开启，储层改造体积减小。在分段分时起裂下，由于先压裂缝内流体滤失，致使缝内净压力显著降低，后续裂缝受到的诱导应力下降，裂缝偏转角度过小，不能很好地沟通远端天然裂缝，形成缝网。因此，可通过优化簇间距减小应力干扰，避免井口憋压，并通过缩短压裂段的施工间隔时间提高段和段之间的诱导应力，促使相邻段的裂缝有足够大的偏转角度。但在“井工厂”模式下，各压裂工艺对诱导应力的适应条件和优化方法不一样。从图10(b)可知，当诱导应力小于0.75 MPa时(图中虚线所示位置)，常规拉链式压裂工艺下裂缝偏转角度比其他2种工艺的大，说明在此工艺下，减小段间距或井间距可最大程度地利用诱导应力的干扰作用使裂缝转向，常规拉链式压裂工艺优于逐次顺序压裂工艺和改进拉链式压裂工艺。当诱导应力大于0.75 MPa 且水力裂缝偏转相同角度时，改进拉链式压裂工艺所需要的诱导应力增量最小，此时，减小段间距或井间距能够更好地沟通远端天然裂缝，形成复杂缝网。这说明当近井地层天然裂缝密度较高时，可优先考虑常规拉链式压裂工艺，并通过小幅度缩小段间距和井间距优化诱导应力场分布，达到沟通天然裂缝的目的。当近井地层天然裂缝密度较低或离井眼有一定距离时，应大幅度减小段间距或增大井间距诱导应力并选择改进拉链式压裂工艺。因此，现场应根据具体的地质特征，选择合适的改造工艺。

图10 裂缝形态与诱导应力的关系Fig.10 Relationship between fracture morphology and induced stress

3.3.2 诱导应力对裂缝长度的影响

诱导应力与裂缝长度损失率之间的关系见图11。由图11可知：诱导应力场越大，裂缝长度损失率越高；裂缝长度损失主要集中在诱导应力小于1 MPa时；当诱导应力大于1 MPa时，裂缝长度有损失的数量下降，说明此时裂缝长度对诱导应力不敏感。通过对比图7(b)和图10(b)可以看到：7号裂缝虽然受到0.6 MPa的诱导应力，但并未发生角度偏转，而裂缝上下半长出现严重的不均等扩展，整个裂缝模态出现单翼发育的情况。这说明诱导应力场对井筒两侧上下半缝长的均等扩展具有很强的影响。不同压裂工艺下7号裂缝长度随时间的变化见图12。从图12(a)可以看出：在常规拉链式压裂时，不均等裂缝上下半长(绝对值)不是同时扩展，被“压制”的裂缝半长起裂时间晚于“优势”的一方，此时，井筒两侧诱导应力差达1 MPa。从图12(b)可以看出：通过改变压裂工艺，7号裂缝在改进拉链式压裂时井筒两侧的沿裂缝面路径上诱导应力分布差异减小，差值为0.2 MPa，此时，裂缝上下半长同步扩展。图13所示为沿7 号裂缝面不同时刻的最大主应力变化规律。从图13可知：改变压裂工艺后，裂缝在起裂过程中，上、下半长的最大主应力也较均匀。这说明在裂缝起裂前，裂缝半长竞争关系就已经明确，主要由已压裂井在井筒两侧的叠加应力差值决定，且诱导应力小的一侧裂缝优先扩展；当井筒两侧诱导应力场差值较小时，裂缝上下半长同步扩展。裂缝上下半长不均匀扩展性已在多个井下微地震监测项目中得到证实，本研究揭示了导致这种现象的本质原因，为压裂优化设计提供了方向。

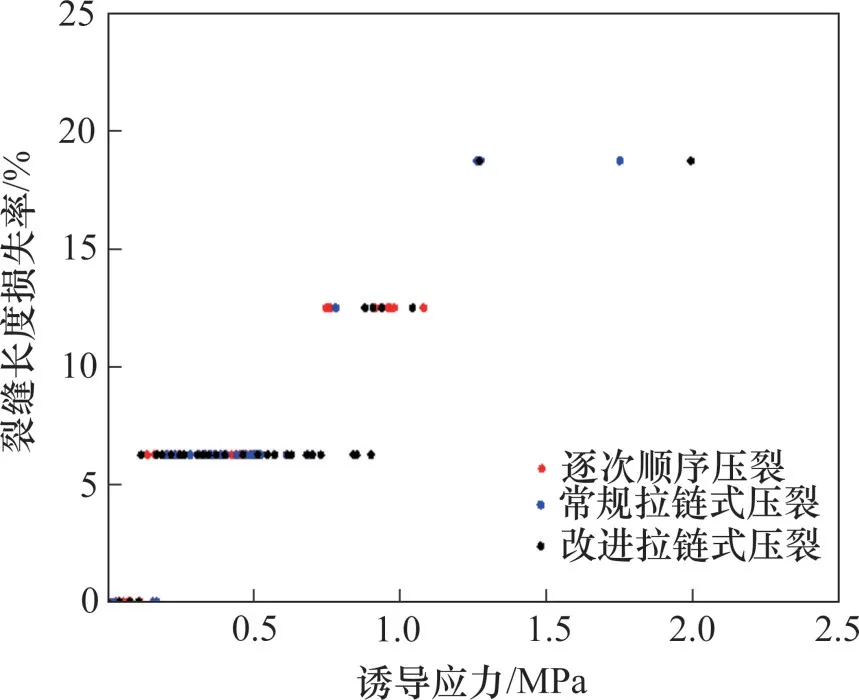
图11 不同压裂模式下诱导应力与裂缝长度损失率关系曲线Fig.11 Relationship between induced stress and fracture length loss rate

图12 不同模式下裂缝起裂时间对比图Fig.12 Comparison of fracture opening time under different modes

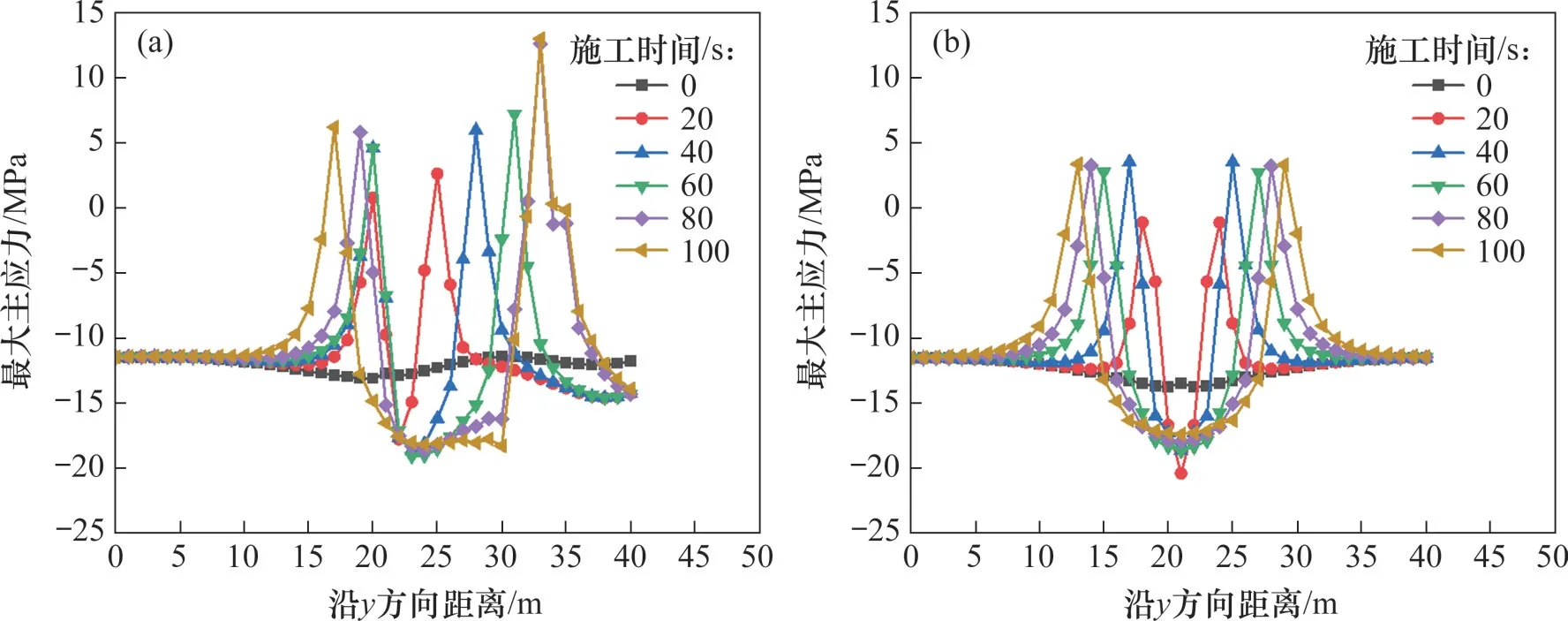
图13 沿7号裂缝面不同起裂时刻最大主应力分布Fig.13 The maximum principal stress distribution of no.7 fracture surface at different initiation time

3.3.3 诱导应力场对裂缝宽度的影响

压裂施工过程中要求缝口宽度大于支撑剂粒径3倍以上，因此，有必要分析不同压裂工艺下诱导应力对近井缝口宽度的影响。3种压裂工艺下近井筒裂缝宽度随时间的变化见图14(a)～(c)，路径2、路径4 的诱导应力和近井筒裂缝宽度曲线见图14(d)。由图14可知：整体上，近井筒裂缝宽度随着诱导应力的增大而减小，其中逐次顺序压裂拟合公式为y=0.018-0.006x(R2=0.93)，常规拉链式压裂为y=0.005e(-x/0.405)+0.014(R2=0.91)，改进拉链式压裂为y=0.006e(-x/0.504)+0.013(R2=0.88)；增大诱导应力后，裂缝宽度减小。但在“井工厂”模式下，2口井的表现形式不同。从图14(a)可以看出在逐次顺序压裂工艺下，2口井中各缝受到的诱导应力较小，裂缝宽度主要由压裂液黏度、排量等施工因素控制，诱导应力对裂缝宽度的影响较为线性；从图14(b)可以看出在常规拉链式压裂模式下，由于井间诱导应力增大，水平井2根部裂缝在叠加应力场影响下，裂缝宽度变窄；从图14(c)可以看出，在改进拉链式压裂工艺下，3号裂缝、6号裂缝、7号裂缝和8号裂缝的缝宽增加，这是因为在井间拉诱导应力作用下，抵消掉了近水平井2 缝间的压诱导应力，在同样施工条件下，缝内净压力升高，裂缝宽度增加，水平井1和水平井2的各条裂缝宽度都能得到保证。因此，在埋地较深的页岩地层，当地层破裂压裂较高、需要更大的缝内净压力时，优先考虑改进拉链式压裂作业方式，这既可以保证有足够的诱导应力促使裂缝转向形成缝网，又可以维持缝宽，降低后压井施工风险。

图14 近井筒裂缝宽度随时间变化曲线Fig.14 Curves of fracture width changing near wellbore with time

4 结论

1) 逐次顺序压裂工艺下的诱导应力最小，偏转角度较小，不利于缝网形成。常规拉链式压裂增大了缝间和井间的诱导应力场，裂缝扩展偏离最大主应力方向，但裂缝长度较逐次压裂的裂缝长度有所减小。改进拉链式压裂工艺可有效降低井间干扰，提高后压井的裂缝宽度，并在保证裂缝偏转的同时，维持裂缝长度，适用于破裂压裂较高的页岩储层。

2) 段间距的增加可有效降低诱导应力，并可以调整常规拉链式压裂模式下诱导应力波动情况。改进拉链式压裂对井间距调整敏感，增大井间距可降低后压井各缝受到的缝间应力干扰，诱导应力分布形态与逐次顺序压裂的相似，降低了施工风险。

3) 诱导应力沿井轴两侧的均匀程度以及差值影响裂缝上下半长的起裂时间和扩展长度。诱导应力小的一侧裂缝优先扩展，直至井筒两侧叠加应力场相近时，被“压制”一侧裂缝开始扩展。可通过调整段间距和井间距优化诱导应力场在井筒两侧的分布方式，使裂缝同步扩展，增大储层的改造体积。